Презентация содержит 24 слайда.

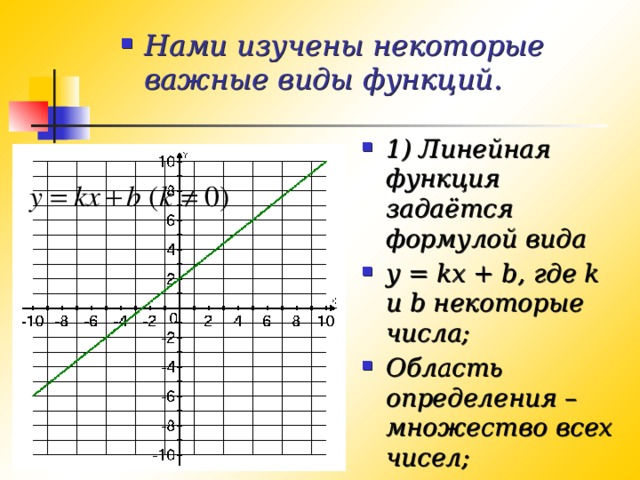
Функцией называют такую зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение переменной y.
Переменную x называют независимой переменной или аргументом.
Переменную y называют зависимой переменной.
Переменная y является функцией от переменной x.
Значения зависимой переменной называют значениями функции.
Если зависимость переменной yот переменной xявляется функцией, то коротко это записывают так:
y = f(x).
Пример № 1.
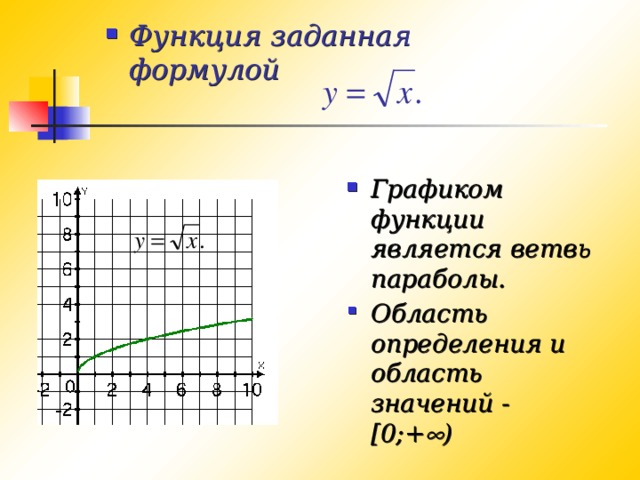
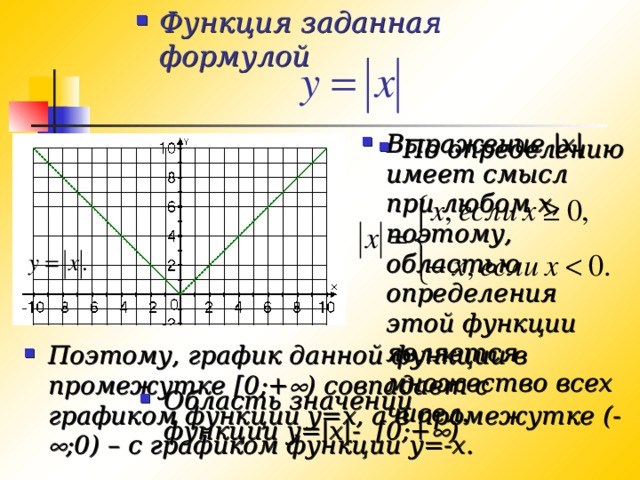
Функция задана формулой
y = 2x2 – 6 или f(x) = 2x2 – 6.
Найдите: f(1); f(2,5); f(-3).
Решение.
f(1) = 2·12 – 6 = 2 – 6 = -4;
f(2,5) = 2 · 2,52 – 6 = 2 · 6,25 – 6 = 12,5 – 6 = 6,5;
f(-3) = 2 · (-3)2 – 6 = 18 – 6 = 12.
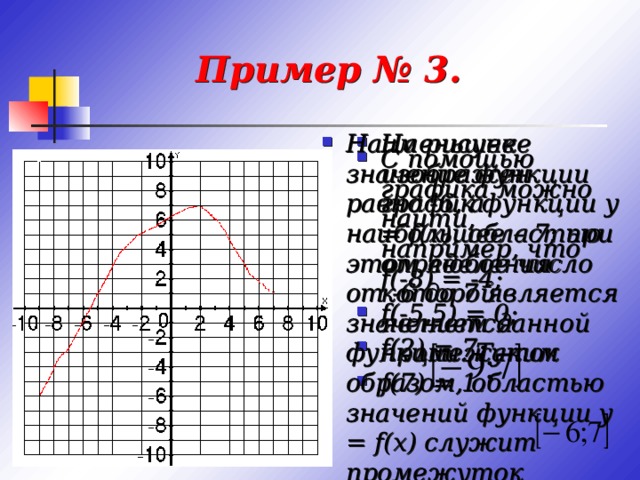
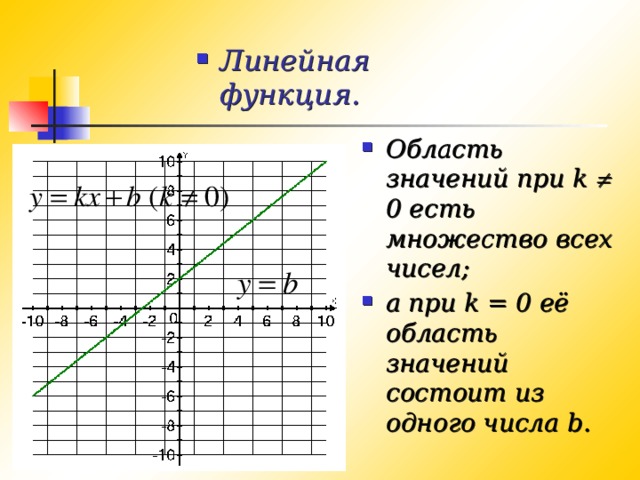
Все значения независимой переменной образуют область определения функции.
Все значения, которые принимает зависимая переменная, образуют область значений функции.
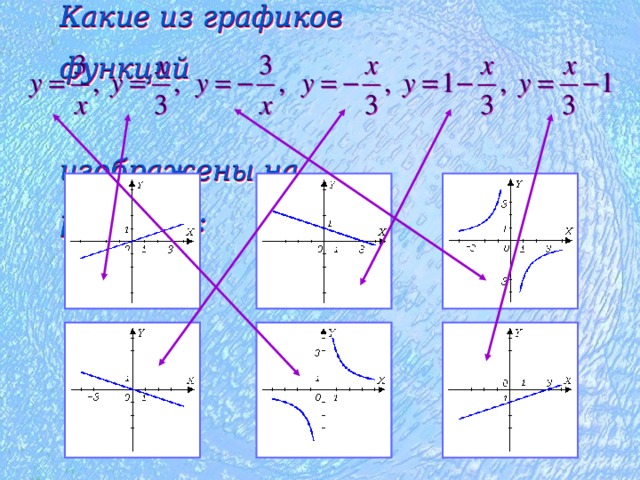
Упражнение
Известно, что f(x) = -5x + 6.
Найдите x при котором:
f(x) = 17; f(x) = -3; f(x) = 0.

 Получите свидетельство
Получите свидетельство Вход
Вход

























 Функция, область определения и область значений (1.08 MB)
Функция, область определения и область значений (1.08 MB)
 1
1 4736
4736 1351
1351 Нравится
0
Нравится
0









