Цель:
Образовательная: Обобщить пройденный материал. Ввести определение показательной функции; Сформулировать её основные свойства;
Показать построение графиков функции, используя программу «Живая математика»
Развивающая: Создать условия для развития логического мышления, развивать
умение анализировать и внимание.
Воспитательная: Воспитывать самостоятельность, расширить кругозор учащихся.
Методы: словесный, объяснительно - иллюстративный, частично - поисковый.
Оборудование:
компьютер, планшет.
Дополнительные интернет - ресурсы: I
1. Цифровые образовательные ресурсы http://school - collection. edu. ru/
2. Материалы i - класса “Алгебра и начала анализа, 10 класс”
3. презентация.
Ход урока
I. Организационный момент ( приветствие , проверка общего доступа, наличие обратной связи, внешнего вида и самочувствия ребенка)
II. Проверка домашнего задания и знаний ученика(цы)
III. Изучение нового материала:
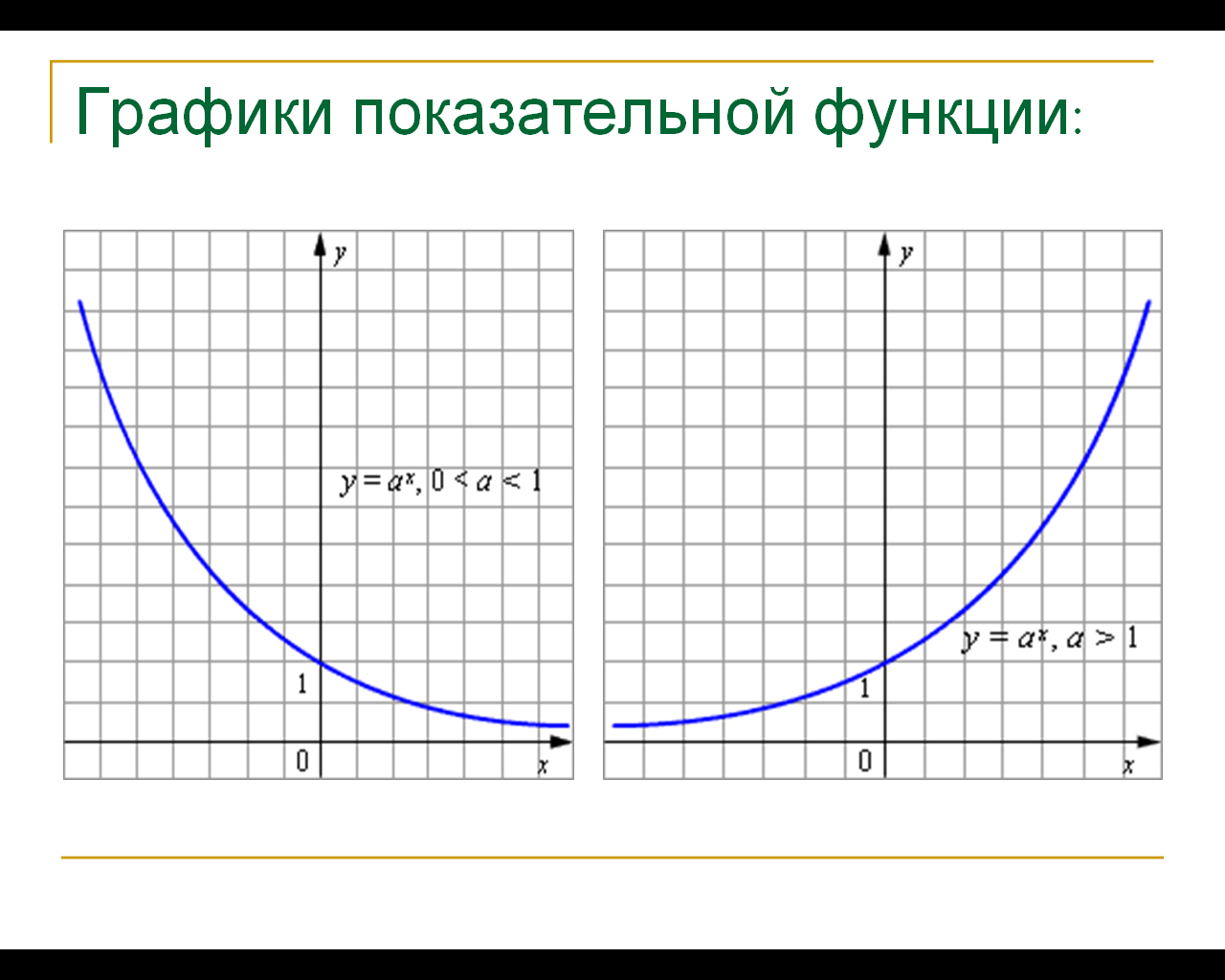
- Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией.
- Область определения показательной функции: D (y)=R – множество всех действительных чисел.
- Область значений показательной функции: E (y)=R+ - множество всех положительных чисел.
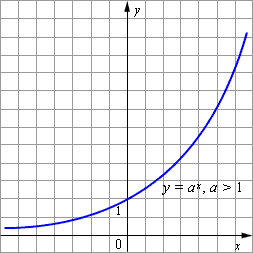
- Показательная функция y=ax возрастает при a>1.
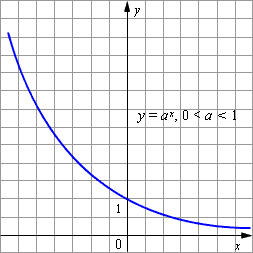
- Показательная функция y=ax убывает при 0<a<1.
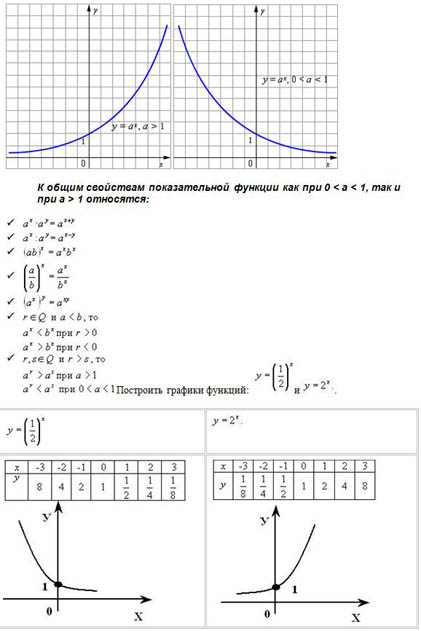
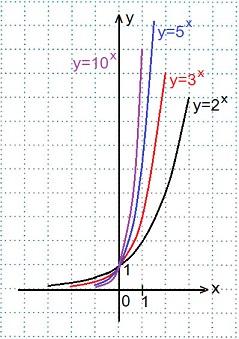
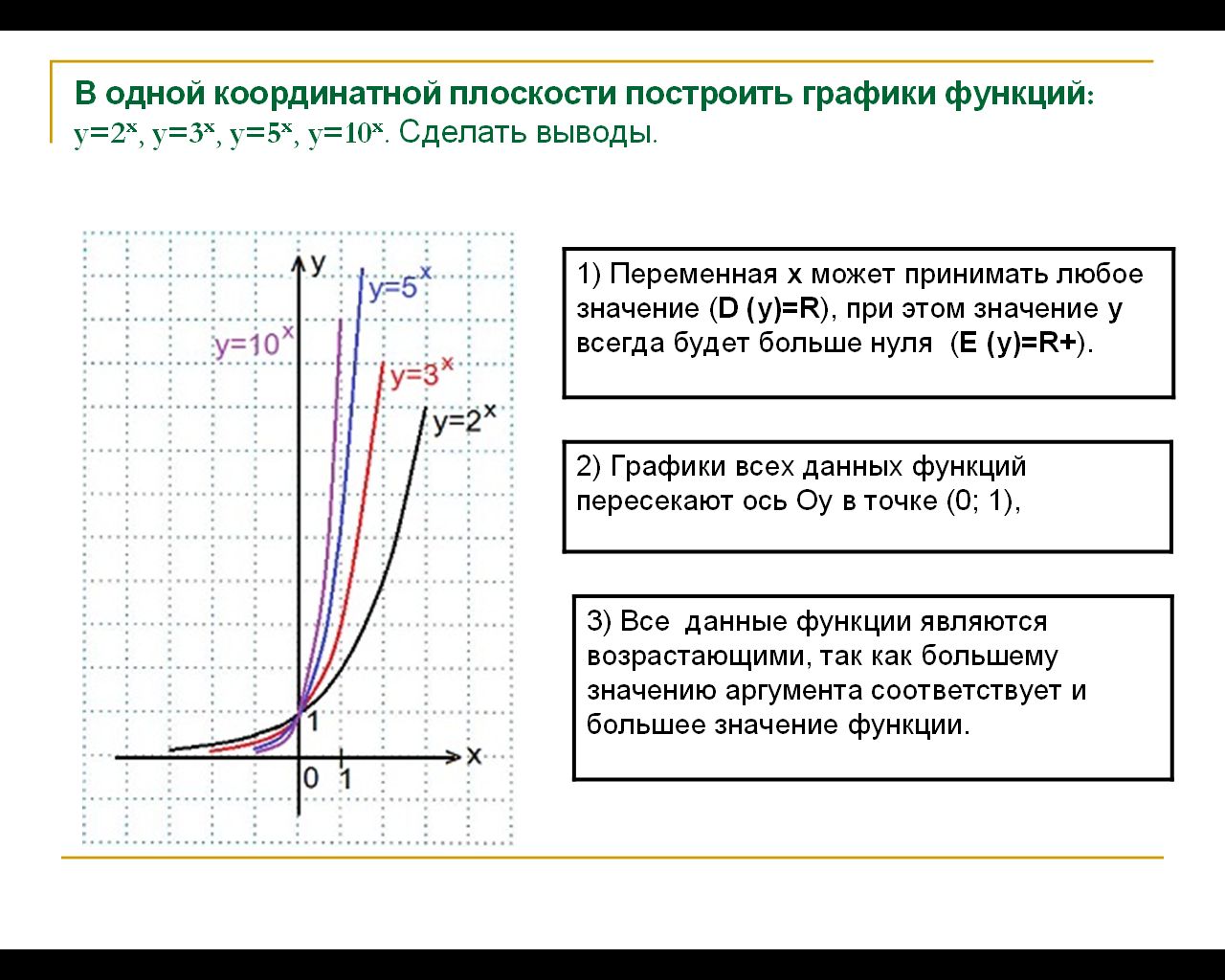
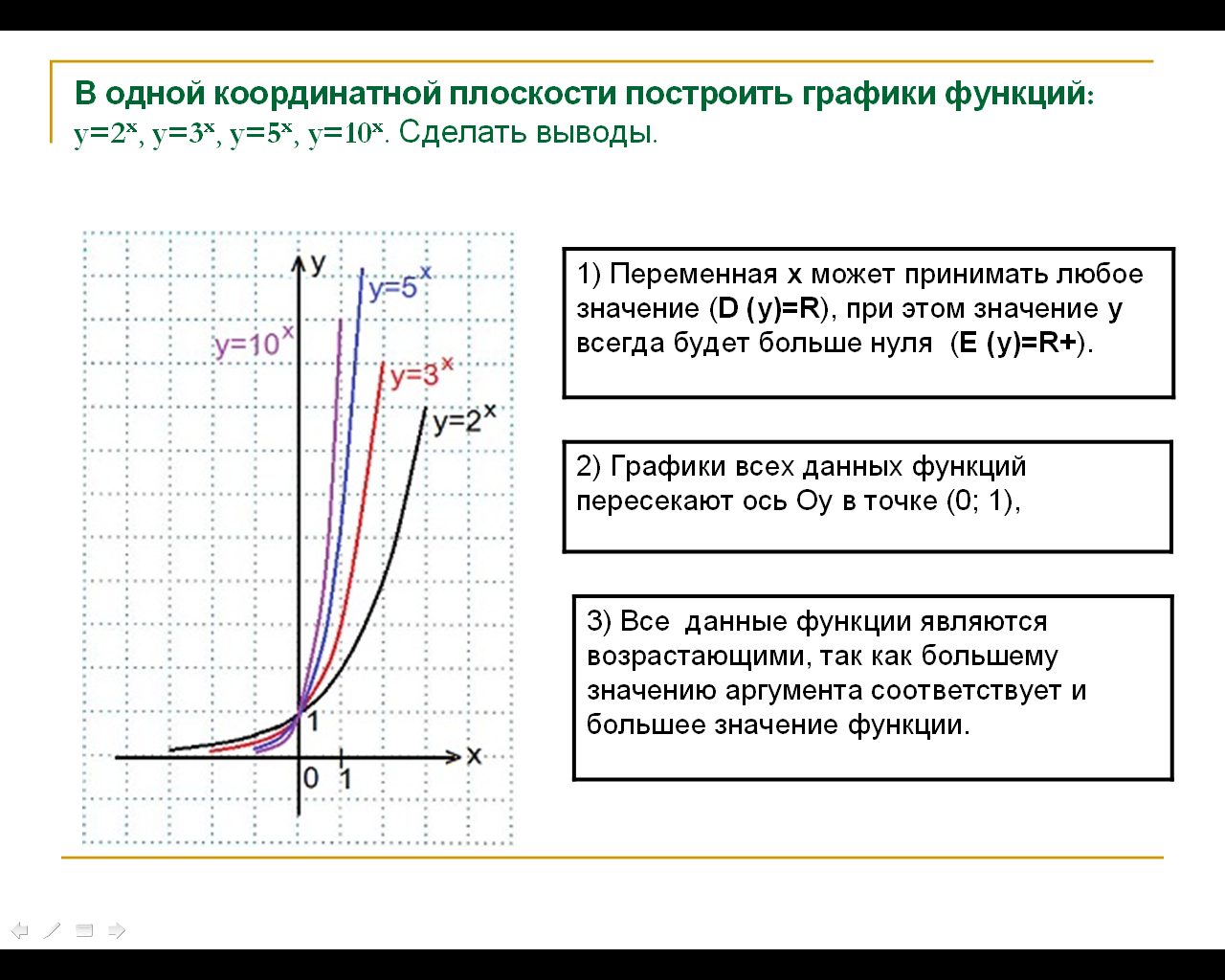
Задание для выполнения в программе «Живая математика»: В одной координатной плоскости построить графики функций:
y=2x, y=3x, y=5x, y=10x. Сделать выводы.
График функции у=2х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.
(Слайд презентации № 6)
Выводы:
1) Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
2) Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание а (если a>1) показательной функции у=ах, тем ближе расположена кривая к оси Оу.
3) Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
Сделать задание в тетради:
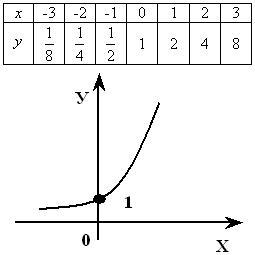
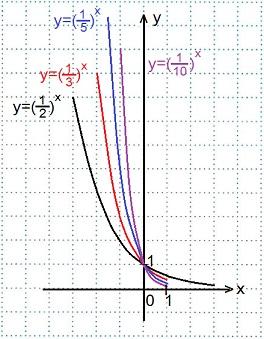
y=(1/2)x, y=(1/3)x, y=(1/5)x, y=(1/10)x. Сделать выводы. . (Слайды презентации № 7)
Смотрите построение графика функции y=(1/2)x выше, графики остальных функций строим аналогично, вычислив их значения при х=0 и при х=±1.
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход



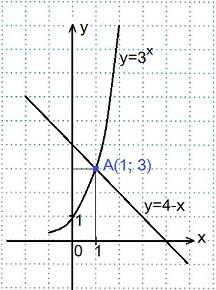
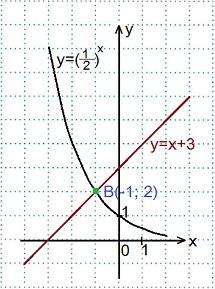
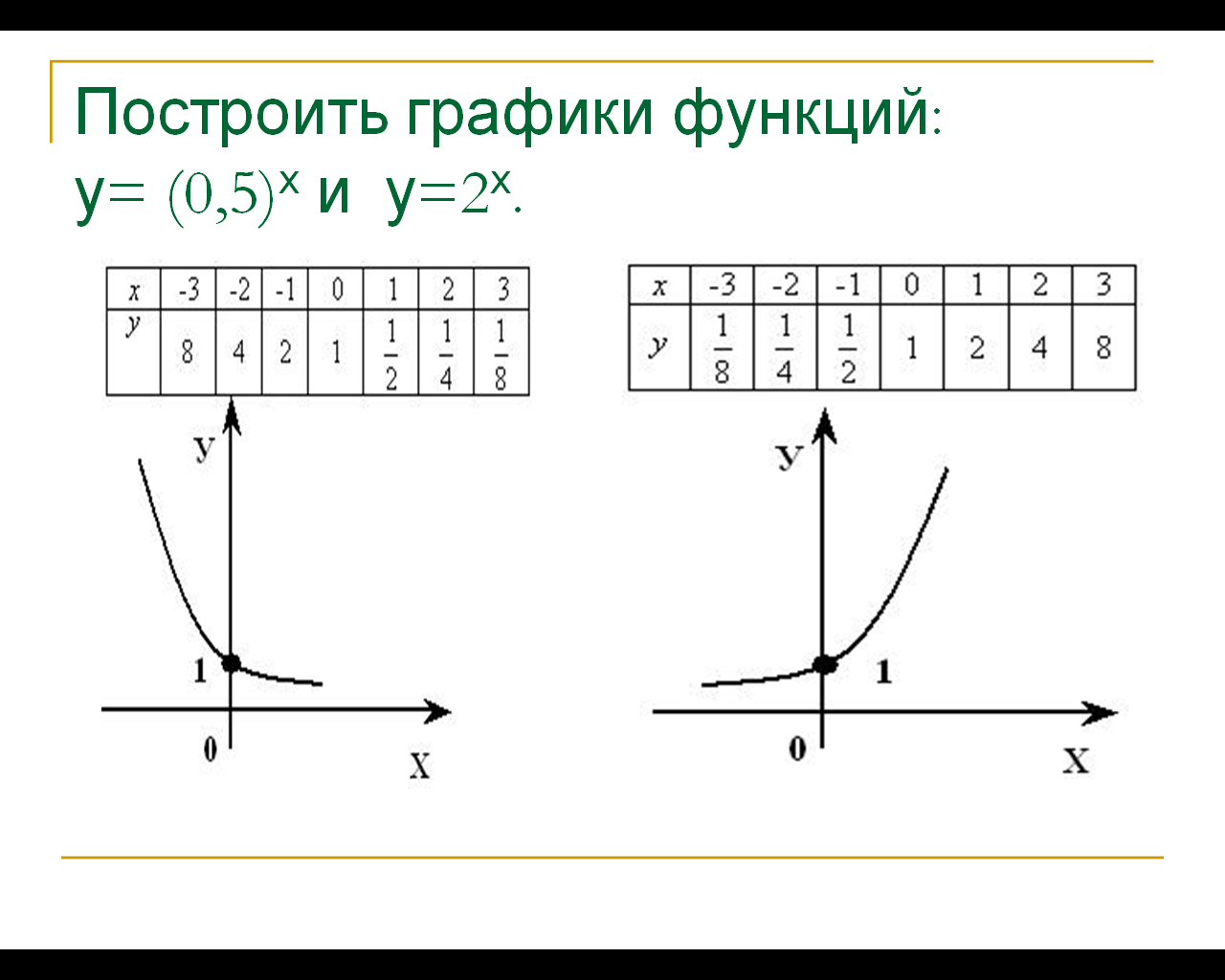
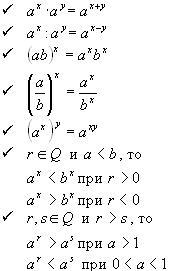 Построить графики функций:
Построить графики функций: 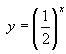 и
и 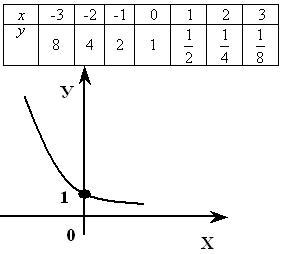












 Урок математики "Показательная функция, её свойства и график" (2.17 MB)
Урок математики "Показательная функция, её свойства и график" (2.17 MB)
 0
0 3325
3325 509
509 Нравится
0
Нравится
0


