Методическая разработка по математике "Показательные уравнения"

Пояснительная записка

Методическая разработка теоретического занятия по дисциплине  «Математика» на тему «Показательные уравнения» из раздела «Показательная функция» составлена на основе Рабочей программы по математике и календарно-тематического плана. Тема занятия  взаимосвязана содержанием, основными положениями.

Программный материал данного занятия базируется на знаниях математики. Рассматриваются вопросы:

- Показательная функция свойства и график.

- Показательные уравнения и методы их решения.

Методическая разработка теоретического занятия составлена для проведения теоретического занятия по математике для студентов 1 года обучения.

 Тип занятия: комбинированное занятие – с элементами беседы и выполнением упражнений.

Цели занятия:

Образовательные:

- формирование научного мировоззрения учащихся, акцентируя внимание на методы решения показательных уравнений.

- формирование  знаний в усвоении понятия показательной функции.

- формирование знаний в усвоении  решения показательных уравнений.

Развивающие:

- развивать мышление учащихся, интерес к изучению математики, развитие, повторение, углубление и систематизация имеющихся у студентов  сведений о решении показательных уравнений, сводящихся к квадратным.

Воспитательные:

- воспитывать сознательное отношение к учебе и заинтересованность в изучении математики.

Средства обучения:

- Методическая разработка по теме.

- Электронная презентация по теме.

- Персональный компьютер, медиапроектор.

- Электронное приложение к учебнику  Ш.А Алимов. Издательство «Просвещение».

Дидактический материал:

Учебник «Алгебра и начала математического анализа» Ш. А. Алимов Упражнения на стр. 79

Внутрипредметные связи: квадратные уравнения и показательные уравнения.

Межпредметные связи: алгебра и матанализ.

Студент должен знать:

-  определение показательной функции (формулу), показательных уравнений.

-  три основных свойства показательной функции.

Студент должен уметь:

- решать показательные уравнения, используя различные методы.

- строить график показательной функции .

План занятия

1. Организационный момент – 2 мин.

2. Вводная мотивация: постановка целей, изложение плана урока – 3 мин.

3. Проверка домашнего задания – 10 мин.

4. Изучение нового материала – 45 мин.

Основной материал, с использованием электронной презентацией по теме: «Методы решения показательных уравнений»

5. Закрепление материала:  Решение задач № 208-210 на стр. 79 – 25 мин.

6. Подведение итогов – 3 мин.

7. Домашнее задание – 2 мин.  §12 Упражнение  № 208-210 четные.

Ход урока:

1. Организационный момент.

2. Вводная мотивация: постановка целей, изложение плана урока.

3. Проверка домашнего задания – 10 мин. Письменно на доске проверка № 196-200 (четные).

4. Изучение нового материала – 45 мин.

Основной материал, с использованием электронной презентацией по теме: «Методы решения показательных уравнений».

Слайд №1

Определение показательной функции:

Функция вида y = a^x, где a больше нуля и а не равно единице называется показательной функцией.

Слайд № 2:

Основные свойства показательной функции:

1. Областью определения показательной функции будет являться множество вещественных чисел.

2. Область значений показательной функции будет являться множество всех положительных вещественных чисел. Иногда это множество для краткости записи обозначают как R+.

Весь материал - в документе.

Филиал боу СПО «ЧЕБОКСАРСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ» минздравсоцразвития чувашии Г. КАНАШ чувашской республики

«Утверждаю»

зав учебной части

Филиал

БОУ СПО «ЧМК»

г. Канаш

_______Фадеева Т.Э

«____» ________2013 г.

Методическая разработка

Теоретического занятия по дисциплине ОДП.06 Математика

«Показательные уравнения»

Для специальности:

060501 «Сестринское дело»

Разработала преподаватель

математики и физики

Cеменова А.М

Рассмотрена

на заседании ЦМК ОГСЭ

дисциплин

протокол №____

«____» _______2013 г

Председатель ЦМК

_________ Романова Л.В

Канаш 2013 г.

Пояснительная записка

Методическая разработка теоретического занятия по дисциплине «Математика» на тему «Показательные уравнения» из раздела «Показательная функция» составлена на основе Рабочей программы по математике и календарно-тематического плана. Тема занятия взаимосвязана содержанием, основными положениями.

Программный материал данного занятия базируется на знаниях математики. Рассматриваются вопросы: - Показательная функция свойства и график.

- Показательные уравнения и методы их решения.

Методическая разработка теоретического занятия составлена для проведения теоретического занятия по математике для студентов 1 года обучения.

Аннотация

Методическая разработка теоретического занятия по теме «Показательные уравнения» включает программный теоретический материал раздела «Показательной функции», материал для изучения решения уравнений студентами и оценка их знаний, вопросы и упражнения для закрепления теоретического занятия, использование электронной презентации.

Методическая разработка теоретического занятия по теме «Показательные уравнения» рекомендуется к использованию преподавателям математики и студентам 1 года обучения.

План теоретического занятия.

Специальность: 060501 Дисциплина ОДБ. 06 Математика

Тема : «Показательные уравнения»

Тип занятия: комбинированное занятие – с элементами беседы и выполнением упражнений.

Цели занятия:

Образовательные:

- формирование научного мировоззрения учащихся, акцентируя внимание на методы решения показательных уравнений.

- формирование знаний в усвоении понятия показательной функции.

- формирование знаний в усвоении решения показательных уравнений.

Развивающие: - развивать мышление учащихся, интерес к изучению математики, развитие, повторение, углубление и систематизация имеющихся у студентов сведений о решении показательных уравнений, сводящихся к квадратным.

Воспитательные: - воспитывать сознательное отношение к учебе и заинтересованность в изучении математики.

Средства обучения:

- Методическая разработка по теме.

- Электронная презентация по теме.

- Персональный компьютер, медиапроектор.

- Электронное приложение к учебнику Ш.А Алимов. Издательство «Просвещение».

Дидактический материал:

Учебник «Алгебра и начала математического анализа» Ш. А. Алимов Упражнения на стр. 79

Внутрипредметные связи: квадратные уравнения и показательные уравнения.

Межпредметные связи: алгебра и матанализ.

Студент должен знать:

- определение показательной функции (формулу), показательных уравнений.

- три основных свойства показательной функции.

Студент должен уметь:

- решать показательные уравнения, используя различные методы.

- строить график показательной функции .

План занятия

1.Организационный момент – 2 мин.

2.Вводная мотивация: постановка целей, изложение плана урока – 3 мин.

3.Проверка домашнего задания – 10 мин.

4.Изучение нового материала - 45 мин.

Основной материал, с использованием электронной презентацией по теме: «Методы решения показательных уравнений»

5.Закрепление материала: Решение задач № 208-210 на стр. 79 – 25 мин.

6.Подведение итогов – 3 мин.

7. Домашнее задание – 2 мин. §12 Упражнение № 208-210 четные.

Ход урока:

1. Организационный момент .

2. Вводная мотивация: постановка целей, изложение плана урока.

3. Проверка домашнего задания – 10 мин. Письменно на доске проверка № 196-200 (четные).

4. Изучение нового материала - 45 мин.

Основной материал, с использованием электронной презентацией по теме: «Методы решения показательных уравнений».

Слайд №1

Определение показательной функции:

Функция вида y = a^x, где a больше нуля и а не равно единице называется показательной функцией.

Слайд № 2:

Основные свойства показательной функции:

1. Областью определения показательной функции будет являться множество вещественных чисел.

2. Область значений показательной функции будет являться множество всех положительных вещественных чисел. Иногда это множество для краткости записи обозначают как R+.

3. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0

4. Справедливы будет все основные свойства степеней. Основные свойства степеней представлены следующим равенствами:

Слайд №3:

a^x*a^y = a^{(x + y);}

(a^x)/(a^y) = a^(x-y);

(a*b)^x = (a^x)*(a^y);

(a/b)^x = a^x/b^x;

(a^x)^y = a^{(x * y)}.

Данные равенства будут справедливы для все действительных значений х и у.

Слайд №4:

5. График показательной функции всегда проходит через точку с координатами (0;1)

6. В зависимости от того возрастает или убывает показательная функция, её график будет иметь один из двух видов:

На следующем рисунке представлен график возрастающей показательной функции: a1.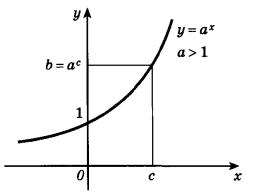

Слайд №5:

На следующем рисунке представлен график убывающей показательной функции: 0

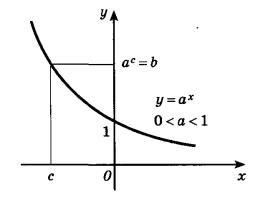
И график возрастающей показательной функции и график убывающей показательной функции согласно свойству, описанному в пятом пункте, проходят через точку (0;1).

Слайд №6:

Показательная функция не имеет точек экстремума, то есть другими словами, она не имеет точек минимума и максимума функции. Если рассматривать функцию на каком-либо конкретном отрезке, то минимальное и максимальное значения функция будет принимать на концах этого промежутка.

8. Функция не является четной или нечетной. Показательная функция это функция общего вида. Это видно и из графиков, ни один из них не симметричен ни относительно оси Оу, ни относительно начала координат.

Слайд №7:

Решение показательных уравнений.

а^x = b - простейшее показательное уравнение. В нем a больше нуля и а не равняется единице.

Слайд №8:

Решение показательных уравнений

Из свойств показательной функции знаем, что ее область значений ограничена положительными вещественными числами. Тогда если b = 0, уравнение не имеет решений. Такая же ситуация имеет место быть, в уравнении где b отрицательное число.

Теперь положим, что b0. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения. Если в показательной функции для основания а выполнено следующее условие 0

Исходя из этого и применяя теорему о корне, получим, что уравнение a^x = b иметь один единственный корень, при b0 и положительном a не равном единице. Чтобы его найти, необходимо представить b в виде b = a^c.

Тогда очевидно, что с будет являться решением уравнения a^x = a^c.

Слайд №9:

Рассмотрим следующий пример: решить уравнение

5^{(x2 - 2*x - 1)} = 25.

Представим 25 как 5², получим:

5^{(x2 - 2*x - 1)} = 5².

Или что равносильно :

x² - 2*x - 1 = 2.

Решаем полученное квадратное уравнение любым из известных способов. Получаем два корня x = 3 и x = -1.

Ответ: 3;-1.

Слайд №10:

Решим уравнение 4^x – 5*2^x + 4 = 0. Сделаем замену: t=2^x и получим следующее квадратное уравнение:

t2 - 5*t + 4 = 0.

Решаем это уравнение любым из известных способов. Получаем корни t₁ = 1 t₂ = 4

Теперь решаем уравнения 2^x = 1

2^х = 2⁰

х = 0

и 2^x = 4.

2^х = 2²

х = 2

Ответ: х =0; х = 2.

5. Закрепление нового материала: Решаем задания №208- 211на стр. 82.

№208

1. 4^х-1 = 1

2. 4^х-1 = 4⁰

3. х-1 = 0

4. х = 1

5. Ответ: х = =1

6. 0,3 ^3х-2 = 1

7. 0,3 ^3х-2 = 0,3⁰

8. 3х – 2 = 0

9. х = 2/3

10. Ответ : х =2/3

1. № 209

1. 27^х = 1/3

1. 3^3х = 3^-1

2. 3 х = -1

3. х = - 1/3

4. Ответ: х = - 1/3

1. (1/5)^х = 25

1. 5^-х = 5²

2. -х = 2

3. х = -2

4. Ответ: х = -2

2. № 210

1. 3^х+1/1 * 3^х-2 = 1

2. 3^{х+1/2 + х -2} = 3⁰

3. 2х – 1,5 = 0

4. 2х = 1,5

5. х = 0,75

6. Ответ: х = 0.75

7. 3)0,6 ^х * 0,6 ³ = 0, 6^2х/0,6 ⁵ х+ 3 = 2 х – 5

8. х – 2х = - 5 – 3

9. - х = - 8

10. х = 8

11. Ответ: х = 8

1. № 211

1. 3^2х+1 +3^2х = 108

1. 3^2х (1/3 +1) = 108

2. 3^2х* 4/3= 108

3. 3^2х = 81

4. 3^2х = 3⁴

5. 2х = 4

6. х = 2

7. Ответ : х = 2

8. 3)2^х+1 + 2^х-1 + 2^х = 28

9. 2^х(2 + ½ + 1) = 28

10. 2^х *7/2 = 28

11. 2^х = 8

12. 2^х = 2³

13. х = 3

14. Ответ: х = 3

2. 6.Подведение итогов – 3 мин.

3. 7. Домашнее задание – 2 мин. §12 Упражнение № 208-211 четные.