Пояснительная записка.
Значение математической подготовки в становлении современного человека определяет следующие общие цели школьного математического образования:
Овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин и продолжения образования.
Интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности.
Формирование представлений об идеях и методах математики, о математики как о форме описания и методе познания действительности.
Формирование представлений о значимости математики как части общечеловеческой культуры.
Реализация этих целей на старшей ступени школы дифференцируется в зависимости от направленности интересов ученика.
Для тех учащихся, кто предполагает получить в дальнейшем высшее образование, связанное с естественными науками, техникой и социально-экономическим дисциплинами, математическая подготовка должна носить более фундаментальный характер.
Предлагаемая программа рассчитана на 2 часа в неделю и ставит свое целью подготовить учащихся к обязательному комплексному тестированию и продолжению образования в ВУЗах, где математика является одним из базовых предметов.
Актуальность данной программы продиктована необходимостью раскрыть теоретические основы изучаемого материала, подчеркнуть причинно-следственные и межпредметные связи. Работа по данной программе может быть начата уже в 10 классе.
Цели:
1. Оказание методической помощи учителя математики;
2. Углубление и теоретизация знаний учащихся по предложенным темам;
3. Становление и развитие познавательной деятельности учащихся;
4. Развитие логического и абстрактного мышления;
5. Воспитание самостоятельности, трудолюбия, творческого отношения к изучаемого материалу и умение адекватно оценивать свою деятельность.
Констатирующая (содержательная) часть.
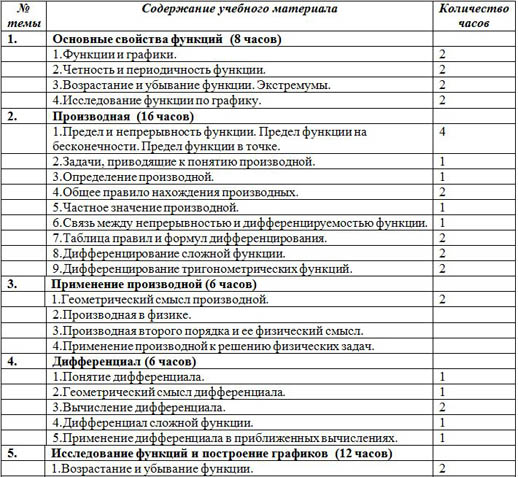
Тема №1. «Основные свойства функции» 8 часов.
Функции и графики. Четность и периодичность. Возрастание, убывание и экстремумы. Исследование функции по графику.
Тема № 2. «Производная» 16 часов.
Понятие предела и непрерывности. Предел функции на бесконечности и в точке. Задачи, приводящие к понятию производной. Определение производной. Правила нахождение производной. Таблица производной. Непрерывность и дифференцируемость. Дифференцирование сложной функции. Дифференцирование тригонометрических функций.
Тема № 3. « Применение производной» 6 часов.
Геометрический смысл производной. Производная в физике. Производная второго порядка и ее физический смысл. Применение производной к решению физических задач.
Тема № 4. «Дифференциал» 6 часов.
Понятие дифференциала и его геометрический смысл. Вычисление дифференциала. Дифференциал сложной функции. Применение дифференциала в приближенных вычислениях.
Тема № 5. «Исследование функций и построение графика» 12 часов.
Возрастание и убывание функции. Исследование с помощью первой и второй производной. Экстремумы функции. Построение графиков.
Тема № 6. «Неопределенный интеграл» 6 часов.
Понятие первообразной. Правила нахождения первообразной. Непосредственное интегрирование. Интегрирование заменой переменной. Определенный интеграл. Формула Ньютона-Лейбница.
Тема № 7. «Дифференциальные уравнения» 4 часа.
Определение дифференциального уравнения. Решение простейших дифференциальных уравнений.
Тема № 8. «Показательная и логарифмическая функции» 10 часов.
Показательная и логарифмическая функции и их графики. Показательные и логарифмические уравнения. Показательные и логарифмические неравенства. Методы их решения.
В качестве приложения разработано календарно-тематическое планирование прикладного курса.
Информационно-методическая часть.
Программа предусматривает межпредметные связи с физикой и геометрией.
Основные формы работы: беседы, лекции, самостоятельная работа учащихся, сочетание различных видов деятельности.
Используется:
Наглядные пособия: плакаты, схемы, таблицы
Технические средства: интерактивная доска, компьютерные программы.
В результате изучения курса, учащиеся должны овладеть следующими знаниями и умениями:
Знать:
Знать определение функции и основные свойства функции.
Знать определение производной, правила и формулы нахождения производной. Геометрический и физический смысл производной первого и второго порядка.
Знать определение и геометрический смысл дифференциала.
Знать определение первообразной и правила ее вычисления, знать таблицу первообразной.
Знать определения показательной и логарифмической функции, знать методы решения показательных и логарифмических уравнений и неравенств.
Уметь:
Уметь определять основные свойства функции, строить графики, исследовать свойства функции по графику.
Уметь находить производные функций.
Уметь записать уравнение касательной к графику функции в указанной точке.
Уметь находить коэффициент наклона касательной к оси абсцисс.
Уметь применять производную при решении физических задач.
Уметь вычислять дифференциал.
Уметь исследовать функции с помощью производной и строить графики.
Уметь вычислять неопределенный интеграл.
Уметь вычислять определенный интеграл использую формулу Ньютона-Лейбница.
Уметь интегрировать методом замены переменной.
Уметь решать простейшие дифференциальные уравнения.
Уметь решать показательные уравнения и неравенства.
Уметь решать логарифмические уравнения и неравенства.
Формы оценки знаний учащихся.
По результатам изучения тем проводиться тематический контроль знаний и умений в любой приемлемой для учителя форме: зачет, разноуровневые тематические тесты, контрольная работа, защита рефератов и презентаций.
Результаты обучения оцениваются по пятибалльной системе.
Оценка устного ответа.
Отметка «5»:
Ответ полный и правильный на основании изученной теории;
Материал изложен в строгой логической последовательности, грамотным математическим языком;
Ответ самостоятельный.
Отметка «4»:
Ответ полный и правильный на основании изученной теории;
Материал изложен в строгой последовательности, грамотным математическим языком, при этом допущены две-три несущественные ошибки, исправленные по требованию учителя.
Оценка «3»:
Ответ полный, но при этом допущены 1-2 существенные ошибки;
Ответ неполный, несвязанный.
Оценка «2»:
Ученик не готов к уроку;
При ответе допущены существенные ошибки, которые ученик не может исправить при наводящих вопросах учителя.
Оценка письменных контрольных работ
Отметка «5»:
Выполнены все задания, на основе изученных теоретических знаний, при этом возможен 1 недочет. Способ решения по выбору учащихся.
Отметка «4»:
Задания выполнены правильно на 80-90%, нет фактических ошибок;
Выполнены все задания, при этом допущена 1 существенная ошибка;
Выполнены все задания, при этом допущены 2-3 несущественные ошибки.
Отметка «3»:
Работа выполнена не менее, чем на половину допущена одна существенная ошибка и при этом в работе имеется 2-3 недочета.
Отметка «2»:
Работа выполнена меньше, чем на половину или содержит несколько существенных ошибок.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Программа прикладного курса по математике "Теоретические основы математического анализа" (10-11 классы) (38.28 КB)
Программа прикладного курса по математике "Теоретические основы математического анализа" (10-11 классы) (38.28 КB)
 0
0 1204
1204 129
129 Нравится
0
Нравится
0





