МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОСТОВСКОЙ ОБЛАСТИ
Государственное казенное оздоровительное образовательное учреждение Ростовской области
санаторного типа для детей, нуждающихся в длительном лечении
САНАТОРНАЯ ШКОЛА - ИНТЕРНАТ №
| Согласовано Руководитель методического объединения «___» ____________ 2013 г.
| Утверждаю директор «___» ___________ 2013 г. |
|
|
|
РАБОЧАЯ ПРОГРАММА
ПО АЛГЕБРЕ
И НАЧАЛАМ МАТЕМАТИЧЕСКОГО АНАЛИЗА
ДЛЯ 11 КЛАССА
НА 2013/2014 УЧЕБНЫЙ ГОД
Учебник: Алгебра и начала анализа
для 10-11 кл. общеобразовательных учреждений/ М.: Просвещение, 2012.
Авторы: Алимов Ш. А., Колягин Ю. М. и др.
Рекомендовано Министерством образования и науки РФ
Разработчик программы
учитель
Мартыненко Н.Н.
Педагогический стаж лет
квалификационная категория.
Ростов-на-Дону
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Рабочая программа по алгебре и началам анализа для 11 класса разработана и составлена в соответствии с федеральным компонентом государственного стандарта начального общего, основного общего и среднего (полного) общего образования. (Приказ МО РФ от 05.03.2004 №1089).
Рабочая программа разработана на основе:
Федерального базисного плана для образовательных учреждений РФ, реализующих программы общего образования. (Приказ МО РФ от 09. 03. 2004г №1312) (с изменениями в редакции приказа от 20.08. 2008 № 241);
Изменений федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования от 03.06.2011 г. № 1994;
Для реализации программного содержания используется следующий учебно-методический комплекс:
Алимов Ш А, Колягин Ю М и др. Алгебра и начала анализа : Учебник для 10-11 кл. общеобразовательных учреждений/ М.: Просвещение, 2012.
Григорьева Г.И. . Поурочное планирование по алгебре и началам анализа 11 кл к учебнику Алимов Ш А, Колягин Ю М и др. Издательство «Учитель» 2008 г Волгоград.
Ивлев Б.М., Саакян С М. Дидактические материалы. Алгебра и начала анализа 11 кл ./ М.: Просвещение, 2007.
-
- МЕСТО ПРЕДМЕТА В БАЗИСНОМ УЧЕБНОМ ПЛАНЕ
Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации для обязательного изучения математики на этапе среднего (полного) общего образования отводится не менее 280 часов из расчета 4 часа в неделю.
Минимальное количество часов преподавания алгебры и начал математического анализа в 11 классе 2 часа в неделю, оптимальное – 3 часа в неделю. Увеличение на 1 час осуществляется за счет использования школьного компонента или за счет часов, отводимых на предпрофильную подготовку.
В основе программы лежат принципы: единства, преемственности, вариативности, системности. Курс строится на индуктивной основе с привлечением дедуктивных рассуждений. Теоретический материал курса излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил и теорем.
- ОБЩАЯ ХАРАКТЕРИСТИКА УЧЕБНОГО ПРЕДМЕТА
При изучении курса алгебры и начала анализа на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа». В рамках указанных содержательных линий решаются следующие задачи:
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
знакомство с основными идеями и методами математического анализа.
- Цели
Изучение математики в старшей школе на базовом уровне направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
-
-
- ОБЩЕУЧЕБНЫЕ УМЕНИЯ, НАВЫКИ И СПОСОБЫ ДЕЯТЕЛЬНОСТИ
В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
- ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ
В результате изучения математики на базовом уровне ученик должен
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира;
Алгебра
уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Начала математического анализа
уметь
вычислять производные и первообразные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
составлять уравнения и неравенства по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Элементы комбинаторики, статистики и теории вероятностей
уметь
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
анализа реальных числовых данных, представленных в виде диаграмм, графиков;
анализа информации статистического характера.
МЕЖПРЕДМЕТНЫЕ И МЕЖКУРСОВЫЕ СВЯЗИ
при работе широко используются:
история – тема «Производная»;
черчение - темы «Геометрический смысл производной», «Применение производной к
исследованию функций», «Интеграл»;
физика – темы «Производная», «Физический смысл производной»;
КРИТЕРИИ ОЦЕНИВАНИЯ
Содержание и объем материала, подлежащего проверке, определяется программой по математике для средней школы. При проверке усвоения этого материала следует выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.
Основными формами проверки знаний и умений учащихся по математике в средней школе являются письменная контрольная работа и устный опрос. При оценке письменных и устных ответов учитель в первую очередь учитывает показанные учащимися знания и умения (их полноту, глубину, прочность, использование в различных ситуациях). Оценка зависит также от наличия и характера погрешностей, допущенных учащимися.
Среди погрешностей выделяются ошибки и недочеты. Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе.
К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в соответствии с программой основными. Недочетами также являются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения: неаккуратная запись, небрежное выполнение чертежа.
Граница между ошибками и недочетами является в некоторой степени условной. При одних обстоятельствах допущенная учащимися погрешность может рассматриваться учителем как ошибка, в другое время и при других обстоятельствах - как недочет.
Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а устное изложение и письменная запись ответа математически грамотны и отличаются последовательностью и аккуратностью.
Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
Оценка ответа учащегося при устном и письменном опросе проводится по пятибалльной системе, т.е. за ответ выставляется одна из отметок: "5" (отлично), "4" (хорошо), "3" (удовлетворительно), "2" (неудовлетворительно), "1" (плохо).
ОЦЕНКА УСТНЫХ ОТВЕТОВ ОБУЧАЮЩИХСЯ
Ответ оценивается отметкой "5", если ученик:
1. полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя.
Возможны одна-две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой "4", если удовлетворяет в основном требованиям на оценку "5", но при этом имеет один из недостатков:
1. в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;
2. допущены один-два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
3. допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка "3" ставится в следующих случаях:
1. неполно раскрыто содержание материала (содержание изложено фрагментально, не всегда последовательно), не показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные "требования к математической подготовке учащихся") в настоящей программе по математике;
2. имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
3. ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
4. при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка "2" ставится в следующих случаях:
1. не раскрыто основное содержание учебного материала;
2. обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
3. допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка "1" ставится, если:
4. ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.
ОЦЕНКА ПИСЬМЕННЫХ КОНТРОЛЬНЫХ РАБОТ ОБУЧАЮЩИХСЯ
Отметка "5" ставится, если:
1. работа выполнена полностью;
2. в логических рассуждениях и обосновании решения нет пробелов и ошибок;
3. в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка "4" ставится в следующих случаях:
1. работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не явилось специальным объектом проверки);
2. допущена одна ошибка или есть два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка "3" ставится, если:
3. допущено более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся обладает обязательными умениями по проверяемой теме.
Отметка "2" ставится, если:
1. допущены существенные ошибки, показавшие, что учащийся не обладает обязательными умениями по данной теме в полной мере.
Отметка "1" ставится, если:
1. работа показала полное отсутствие у учащихся обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им каких-либо других заданий.
ВИДЫ УРОКОВ
Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, изучение свойств различных функций, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Урок-исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке. Любой учащийся может использовать компьютерную информационную базу по методам решения различных задач, по свойствам элементарных функций и т.д.
Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня обученности учащихся, тренировки технике тестирования. Тесты предлагаются как в печатном так и в компьютерном варианте. Причем в компьютерном варианте всегда с ограничением времени.
Урок-зачет. Устный опрос учащихся по заранее составленным вопросам, а также решение задач разного уровня по изученной теме.
Урок-самостоятельная работа. Предлагаются разные виды самостоятельных работ: двухуровневая – уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5»; большой список заданий разного уровня, из которого учащийся решает их по своему выбору. Рядом с учеником на таких уроках – включенный компьютер, который он использует по своему усмотрению.
Урок-контрольная работа. Проводится на двух уровнях:
уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5».
КОМПЬЮТЕРНОЕ ОБЕСПЕЧЕНИЕ УРОКОВ
В разделе рабочей программы «Компьютерное обеспечение» спланировано применение имеющихся компьютерных продуктов: демонстрационный материал, задания для устного опроса учащихся, тренировочные упражнения, а также различные электронные учебники.
Демонстрационный материал (слайды).
Создается с целью обеспечения наглядности при изучении нового материала, использования при ответах учащихся. Применение анимации при создании такого компьютерного продукта позволяет рассматривать вопросы математической теории в движении, обеспечивает другой подход к изучению нового материала, вызывает повышенное внимание и интерес у учащихся.
Изучение многих тем в математике связано с знанием и пониманием свойств элементарных функций. Решение уравнений, неравенств, различных задач предполагает глубокое знание поведения элементарных функций. Научиться распознавать графики таких функций, суметь рассказать об их свойствах помогают компьютерные слайды .
При решении любых задач использование графической интерпретации условия задачи, ее решения позволяет учащимся понять математическую идею решения, более глубоко осмыслить теоретический материал по данной теме.
Задания для устного счета.
Эти задания дают возможность в устном варианте отрабатывать различные вопросы теории и практики, применяя принципы наглядности, доступности. Их можно использовать на любом уроке в режиме учитель – ученик, взаимопроверки, а также в виде тренировочных занятий.
Тренировочные упражнения.
Включают в себя задания с вопросами и наглядными ответами, составленными с помощью анимации. Они позволяют ученику самостоятельно отрабатывать различные вопросы математической теории и практики.
Электронные учебники.
Они используются в качестве виртуальных лабораторий при проведении практических занятий, уроков введения новых знаний. В них заключен большой теоретический материал, много тренажеров, практических и исследовательских заданий, справочного материала. На любом из уроков возможно использование компьютерных устных упражнений, применение тренажера устного счета, что активизирует мыслительную деятельность учащихся, развивает вычислительные навыки, так как позволяет осуществить иной подход к изучаемой теме.
Использование компьютерных технологий в преподавании математики позволяет непрерывно менять формы работы на уроке, постоянно чередовать устные и письменные упражнения, осуществлять разные подходы к решению математических задач, а это постоянно создает и поддерживает интеллектуальное напряжение учащихся, формирует у них устойчивый интерес к изучению данного предмета.
СОДЕРЖАНИЕ КУРСА АЛГЕБРЫ
И НАЧАЛ МАТЕМАТИЧЕСКОГО АНАЛИЗА
11 класс
1. Повторение курса 10 класса
Основные цели:
формирование представлений о целостности и непрерывности курса алгебры;
овладение умением обобщения и систематизации знаний по основным темам курса алгебры 10 класса;
развитие логического, математического мышления и интуиции, творческих способностей в области математики.
2. Тригонометрические функции
Область определения и множество значений тригонометрических функций. Чётность, нечётность, периодичность тригонометрических функций. Свойства и графики функций у=соsx, y=sinx, y=tgx.
Основные цели:
формирование представлений об области определения и множестве значений тригонометрических функций, о нечётной и чётной функциях, о периодической функции, о периоде функции, о наименьшем положительном периоде;
формирование умений находить область определения и множество значений тригонометрических функций сложного аргумента, представленного в виде дроби и корня;
овладение умением свободно строить графики тригонометрических функций и описывать их свойства;
В результате изучения темы учащиеся должны:
знать:
область определения и множество значений элементарных тригонометрических функций;
тригонометрические функции, их свойства и графики;
уметь:
находить область определения и множество значений тригонометрических функций;
множество значений тригонометрических функций вида kf(x) m, где f(x) - любая тригонометрическая функция;
доказывать периодичность функций с заданным периодом;
исследовать функцию на чётность и нечётность;
строить графики тригонометрических функций;
совершать преобразование графиков функций, зная их свойства;
решать графически простейшие тригонометрические уравнения и неравенства.
3. Производная и её геометрический смысл
Производная. Производная степенной функции. Правила дифференцирования. Производные некоторых элементарных функций. Геометрический смысл производной.
Основные цели:
формирование понятий о мгновенной скорости, о касательной к плоской кривой, о касательной к графику функции, о производной функции, о физическом смысле производной, о геометрическом смысле производной, о скорости изменения функции, о пределе функции в точке, о дифференцировании, о производных элементарных функций;
формирование умения использовать алгоритм нахождения производной элементарных функций простого и сложного аргумента;
овладение умением находить производную любой комбинации элементарных функций;
овладение навыками составления уравнения касательной к графику функции при дополнительных условиях, нахождения углового коэффициента касательной, точки касания.
В результате изучения темы учащиеся должны:
знать:
понятие производной функции, физического и геометрического смысла производной;
понятие производной степени, корня;
правила дифференцирования;
формулы производных элементарных функций;
уравнение касательной к графику функции;
алгоритм составления уравнения касательной;
уметь:
вычислять производную степенной функции и корня;
находить производные суммы, разности, произведения, частного;
производные основных элементарных функций;
находить производные элементарных функций сложного аргумента;
составлять уравнение касательной к графику функции по алгоритму;
4. Применение производной к исследованию функций
Возрастание и убывание функций. Экстремумы функции. Применение производной к построению графиков функций. Наибольшее и наименьшее значения функции. Выпуклость графика. Точки перегиба.
Основные цели:
формирование представлений о промежутках возрастания и убывания функции, о достаточном условии возрастания функции, о промежутках монотонности функции, об окрестности точки, о точках максимума и минимума функции, о точках экстремума, о критических точках;
формирование умения строить эскиз графика функции, если задан отрезок, значения функции на концах этого отрезка и знак производной в некоторых точках функции;
овладение умением применять производную к исследованию функций и построению графиков;
овладение навыками исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функций, точки перегиба и интервалы выпуклости.
В результате изучения темы учащиеся должны:
знать:
понятие стационарных, критических точек, точек экстремума;
как применять производную к исследованию функций и построению графиков;
как исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функции;
уметь:
находить интервалы возрастания и убывания функций;
строить эскиз графика непрерывной функции, определённой на отрезке;
находить стационарные точки функции, критические точки и точки экстремума;
применять производную к исследованию функций и построению графиков;
находить наибольшее и наименьшее значение функции;
работать с учебником, отбирать и структурировать материал.
5. Первообразная и интеграл
Первообразная. Правила нахождения первообразных. Площадь криволинейной трапеции и интеграл. Вычисление интегралов. Вычисление площадей с помощью интегралов.
Основные цели:
формирование представлений о первообразной функции, о семействе первообразных, о дифференцировании и интегрировании, о таблице первообразных, о правилах отыскания первообразных;
формирование умений находить для функции первообразную, график которой проходит через точку, заданную координатами;
овладение умением находить площадь криволинейной трапеции, ограниченной графиками функций y = f(x) и y = g(x), ограниченной прямыми x = a. х = b, осью Ох и графиком y = h(x).
В результате изучения темы учащиеся должны:
знать:
понятие первообразной, интеграла;
правила нахождения первообразных;
таблицу первообразных;
формулу Ньютона Лейбница;
правила интегрирования;
уметь:
проводить информационно-смысловой анализ прочитанного текста в учебнике, участвовать в диалоге, приводить примеры; аргументировано отвечать на поставленные вопросы, осмысливать ошибки и их устранять;
доказывать, что данная функция является первообразной для другой данной функции;
находить одну из первообразных для суммы функций и произведения функции на число, используя справочные материалы;
выводить правила отыскания первообразных;
изображать криволинейную трапецию, ограниченную графиками элементарных функций;
вычислять интеграл от элементарной функции простого аргумента по формуле Ньютона Лейбница с помощью таблицы первообразных и правил интегрирования;
вычислять площадь криволинейной трапеции, ограниченной прямыми x = a, х = b, осью Ох и графиком квадратичной функции;
находить площадь криволинейной трапеции, ограниченной параболами;
вычислять путь, пройденный телом от начала движения до остановки, если известна его скорость;
предвидеть возможные последствия своих действий;
владеть навыками контроля и оценки своей деятельности.
6. Элементы комбинаторики
Табличное и графическое представление данных. Числовые характеристики рядов данных.
Поочерёдный и одновременны выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биноминальных коэффициентов. Треугольник Паскаля.
Основные цели:
формирование представлений о научных, логических, комбинаторных методах решения математических задач;
формирование умения анализировать, находить различные способы решения одной и той же задачи, делать выводы;
развитие комбинаторно-логического мышления.
В результате изучения темы учащиеся должны:
знать:
понятие комбинаторной задачи и основных методов её решения (перестановки, размещения, сочетания без повторения и с повторением);
понятие логической задачи;
приёмы решения комбинаторных, логических задач;
элементы графового моделирования;
уметь:
использовать основные методы решения комбинаторных, логических задач;
разрабатывать модели методов решения задач, в том числе и при помощи графового моделирования;
переходить от идеи задачи к аналогичной, более простой задаче, т.е. от основной постановки вопроса к схеме;
ясно выражать разработанную идею задачи.
7. Элементы теории вероятностей
Элементарные и сложные события. Рассмотрение случаев: вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применение вероятностных методов.
Основные цели:
формирование представления о теории вероятности, о понятиях: вероятность, испытание, событие (невозможное и достоверное), вероятность событий, объединение и пересечение событий, следствие события, независимость событий;
формирование умения вычислять вероятность событий, определять несовместные и противоположные события;
овладение умением выполнять основные операции над событиями;
овладение навыками решения практических задач с применением вероятностных методов.
В результате изучения темы учащиеся должны:
знать:
понятие вероятности событий;
понятие невозможного и достоверного события;
понятие независимых событий;
понятие условной вероятности событий;
понятие статистической частоты наступления событий;
уметь:
вычислять вероятность событий;
определять равновероятные события;
выполнять основные операции над событиями;
доказывать независимость событий;
находить условную вероятность;
решать практические задачи, применяя методы теории вероятности.
8. Обобщающее повторение курса алгебры и начал анализа
Основные цели:
обобщение и систематизация курса алгебры и начал анализа;
создание условий для плодотворного участия в групповой работе, для формирования умения самостоятельно и мотивированно организовывать свою деятельность;
формирование представлений об идеях и методах математики, о математике как средстве моделирования явлений и процессов;
развитие логического и математического мышления, интуиции, творческих способностей;
воспитание понимания значимости математики для общественного прогресса.
ПЕРЕЧЕНЬ УЧЕБНО-МЕТОДИЧЕСКОГО ОБЕСПЕЧЕНИЯ:
учебник: базовый уровень". Изд. "Просвещение" М.; 2012.
М.И. Шабунин. "Алгебра и начала математического анализа: дидактические материалы для 11 класса". Изд." Просвещение" М.; 2010.
Н.Е. Федорова. "Изучение алгебры и начал математического анализа в 11 классе: книга для учителя" Изд. "Просвещение" М.; 2008.
М.В. Ткачева. "Алгебра и начала математического анализа: тематические тесты для 11 класса". Изд. "Просвещение" М.; 2009.
Н.И. Фирсова." Математика. 10-11 классы. Тестовые задания к основным учебникам: рабочая тетрадь" Изд. "Эксмо" М.;2010).
А.Л. Семенова, А.Л. Ященко. "Типовые экзаменационные варианты. ФИПИ, ЕГЭ математика " Изд " экзамен" М.; 2013.
Л.Ф. Пичурин. "За страницами учебника алгебры" Изд. "Панарама " М.; 2005.
Д.А. Мальцев. "Алгебра. 10-11 классы. Тематические тесты и упражнения: учебно-методическое пособие" (авторы Каибханова С.З., Мальцева Л.И., Лысенко Р.П., Кирилюк Н.Н., Мальцев А.А., Мальцев Д.А., Монастырская Г.А., Приходько С.В., Старовойт Н.И., Чиркова Е.И.; под редакцией Д.А. Мальцева). НИИ школьных технологий М.; 2011.
Ф.Ф. Лысенко. " Математика. Подготовка к ЕГЭ-2013". Изд "Легион" Ростов на Дону.
Список литературы
-Государственный образовательный стандарт общего образования. // Официальные документы в образовании. - 2004. № 25-25.
-Закон Российской Федерации "Об образовании" // Образование в документах и комментариях. - М.; АСТ "Астрель",2010.
-М.Г. Еремина "Требования к содержанию и оформлению образовательных программ дополнительного образования детей, дошкольных образовательных учреждений и рабочих программ педагогов". Методическое пособие, Калининград, 2010.
-Программа. Планирование учебного материала. Алгебра и начала математического анализа 10-11 классы (автор-составитель Ю.М. Колягин) - М.; Просвещение, 2008.
-Научно-теоретический и методический журнал «Математика в школе»
-Еженедельное учебно-методическое приложение к газете «Первое сентября» Математика
СПИСОК ЛИТЕРАТУРЫ ДЛЯ ОБУЧАЮЩИХСЯ:
1.Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров, Н.Е.Фёдоров, Алгебра и начала анализа 10-11, Москва. Просвещение, 2012.
2.Дидактические материалы для 10-11 классов. Алгебра и начала анализа М.И.Шабунин, М.В.Ткачева, Н.Е.Федорова, Р.Г.Газаврян Москва. Мнемозина,1998.
3.М.В. Ткачева. "Алгебра и начала математического анализа: тематические тесты для 11 класса". Изд. "Просвещение" М.; 2009.
4.Н.И. Фирсова." Математика. 10-11 классы. Тестовые задания к основным учебникам: рабочая тетрадь" Изд. "Эксмо" М.;2010).
5.А.Л. Семенова, А.Л. Ященко. "Типовые экзаменационные варианты. ФИПИ, ЕГЭ математика " Изд " экзамен" М.; 2013.
6.Л.Ф. Пичурин. "За страницами учебника алгебры" Изд. "Панарама " М.; 2005.
7.Д.А. Мальцев. "Алгебра. 10-11 классы. Тематические тесты и упражнения: учебно-методическое пособие" (авторы Каибханова С.З., Мальцева Л.И., Лысенко Р.П., Кирилюк Н.Н., Мальцев А.А., Мальцев Д.А., Монастырская Г.А., Приходько С.В., Старовойт Н.И., Чиркова Е.И.; под редакцией Д.А. Мальцева). НИИ школьных технологий М.; 2011.
8.Ф.Ф. Лысенко. " Математика. Подготовка к ЕГЭ-2013". Изд "Легион" Ростов на Дону.
ИНТЕРНЕТ — РЕСУРСЫ:
http://school-collection.edu.ru/ – единая коллекция цифровых образовательных ресурсов.
http://www.alleng.ru/edu/math3.htm - типовые математические задания ЕГЭ
http://eek.diry.ru/p62222263.htm - подготовка к ЕГЭ по математике
http://reshuege.ru/ - образовательный портал для подготовки к ЕГЭ
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
(3часа в неделю, всего 102 часа).
Повторение курса 10 класса ( 4 часа).
Глава YII. Тригонометрические функции (14 часов, из них 1 час контрольная работа).
Тригонометрические функции y = sin x, y = cos x, y = tg x, y = ctg x, их свойства и графики. Периодичность функции, основной период.
Обратные тригонометрические функции, их графики.
Глава YIII. Производная и ее геометрический смысл (16 часов, из них 1 час контрольная работа).
Понятие о пределе последовательности. Существование предела монотонной последовательности. Длина окружности и площадь круга как пределы последовательностей.
Понятие о непрерывности функции.
Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Производные обратной функции и композиции данной функции с линейной.
Глава IX. Применение производной к исследованию функций (16 часов, из них 1 час контрольная работа).
Применение производной к исследованию функций и построению графиков. Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком. Вторая производная и ее физический смысл.
Глава X. Интеграл ( 13 часов, из них 1 час контрольная работа).
Первообразная. Формула Ньютона–Лейбница. Понятие об определенном интеграле как площади криволинейной трапеции. Примеры применения интеграла в физике и геометрии.
Тема X. Комбинаторика (
Тема XI. Элементы теории вероятностей (10 часов, из них 1 час контрольная работа).
Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов.
Тема XII. Решение систем уравнений и неравенств с двумя переменными (16 часов, из них 1 час контрольная работа).
Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Решение систем неравенств с одной переменной.
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
Итоговое повторение курса алгебры и началматематического анализа (16 часов, из них 2 часа итоговая контрольная работа или тестирование).
УЧЕБНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
по алгебре и началам математического анализа 11 класс
Классы 11/13, 11/16
Количество часов: 102 часа
Всего 97 (11/13), 97 (11/16) часов; в неделю 3 часа
Плановых контрольных уроков - 8, с/р - 20, тестов - 14
Планирование составлено на основе Программы для общеобразовательных школ, гимназий, лицеев. Математика. Дрофа. Москва, 2008 г.
Учебник Алимов Ш А, Колягин Ю М и др. Алгебра и начала анализа
для 10-11 кл. общеобразовательных учреждений/ М.: Просвещение, 2012.
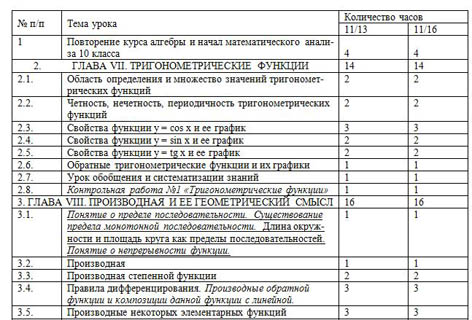
| № п/п | Тема урока | Количество часов |
| 11/13 | 11/16 |
| 1 | Повторение курса алгебры и начал математического анализа 10 класса |
4 |
4 |
| 2. ГЛАВА VII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ | 14 | 14 |
| 2.1. | Область определения и множество значений тригонометрических функций | 2 | 2 |
| 2.2. | Четность, нечетность, периодичность тригонометрических функций | 2 | 2 |
| 2.3. | Свойства функции y = cos x и ее график | 3 | 3 |
| 2.4. | Свойства функции y = sin x и ее график | 2 | 2 |
| 2.5. | Свойства функции y = tg x и ее график | 2 | 2 |
| 2.6. | Обратные тригонометрические функции и их графики | 1 | 1 |
| 2.7. | Урок обобщения и систематизации знаний | 1 | 1 |
| 2.8. | Контрольная работа №1 «Тригонометрические функции» | 1 | 1 |
| 3. ГЛАВА VIII. ПРОИЗВОДНАЯ И ЕЕ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ | 16 | 16 |
| 3.1. | Понятие о пределе последовательности. Существование предела монотонной последовательности. Длина окружности и площадь круга как пределы последовательностей. Понятие о непрерывности функции. | 1 | 1 |
| 3.2. | Производная | 1 | 1 |
| 3.3. | Производная степенной функции | 2 | 2 |
| 3.4. | Правила дифференцирования. Производные обратной функции и композиции данной функции с линейной. | 3 | 3 |
| 3.5. | Производные некоторых элементарных функций | 3 | 3 |
| 3.6. | Геометрический смысл производной. Уравнение касательной к графику функции. | 3 | 3 |
| 3.7. | Урок обобщения и систематизация знаний | 2 | 2 |
| 3.8. | Контрольная работа №2 «Производная и ее геометрический смысл» | 1 | 1 |
| 4. ГЛАВА IX. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ | 16 | 16 |
| 4.1. | Возрастание и убывание функции | 2 | 2 |
| 4.2. | Экстремумы функции | 3 | 3 |
| 4.3. | Применение производной к построению графиков функций. Нахождение скорости для процесса, заданного формулой или графиком. | 3 | 3 |
| 4.4. | Наибольшее и наименьшее значения функции. Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. | 4 | 4 |
| 4.5. | Выпуклость графика функции, точки перегиба | 1 | 1 |
| 4.6. | Вторая производная и ее физический смысл. | 1 | 1 |
| 4.7. | Урок обобщения и систематизации знаний | 1 | 1 |
| 4.8. | Контрольная работа №3 «Применение производной к исследованию функций» | 1 | 1 |
| 5. ГЛАВА Х. ИНТЕГРАЛ | 13 | 13 |
| 5.1. | Первообразная | 2 | 2 |
| 5.2. | Правила нахождения первообразной | 3 | 3 |
| 5.3. | Формула Ньютона–Лейбница. Площадь криволинейной трапеции и интеграл | 3 | 2 |
| 5.4. | Вычисление интеграла. Вычисление площадей с помощью интегралов | 2 | 2 |
| 5.5. | Применение интеграла к решению практических задач | 1 | 1 |
| 5.6. | Урок обобщения и систематизации знаний | 1 | 1 |
| 5.7. | Контрольная работа №4 «Интеграл» | 1 | 1 |
| 6. ГЛАВА XI. КОМБИНАТОРИКА | 9 | 9 |
| 6.1. | Математическая индукция | 1 | 1 |
| 6.2. | Правило произведения | 1 | 1 |
| 6.3. | Размещения с повторениями | 1 | 1 |
| 6.4. | Перестановки | 1 | 1 |
| 6.5. | Размещения без повторений | 1 | 1 |
| 6.6. | Сочетания без повторений и их свойства | 1 | 1 |
| 6.7. | Бином Ньютона | 1 | 1 |
| 6.8. | Сочетания с повторениями | 1 | 1 |
| 6.9. | Контрольная работа №5 «Комбинаторика» | 1 | 1 |
| 7. ГЛАВА XII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ | 8 | 8 |
| 7.1. | События | 1 | 1 |
| 7.2. | Элементарные и сложные события. Вероятность события | 1 | 1 |
| 7.3. | Сложение вероятностей | 1 | 1 |
| 7.4. | Вероятность противоположного события | 1 | 1 |
| 7.5. | Условная вероятность | 1 | 1 |
| 7.6. | Вероятность произведения независимых событий | 1 | 1 |
| 7.7. | Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов | 1 | 1 |
| 7.8. | Контрольная работа №6 «Элементы теории вероятностей» | 1 | 1 |
| 8. ГЛАВА XIII. РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ И НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ | 9 | 9 |
| 8.1. | Равносильность уравнений, неравенств, систем | 1 | 1 |
| 8.2. | Решение простейших систем уравнений с двумя неизвестными | 1 | 1 |
| 8.3. | Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных | 1 | 1 |
| 8.4. | Решение систем неравенств с одной переменной | 1 | 1 |
| 8.5. | Использование свойств и графиков функций при решении уравнений и неравенств | 1 | 1 |
| 8.6. | Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем | 1 | 1 |
| 8.7. | Применение математических методов для решения содержательных задач из различных областей науки и практики | 1 | 1 |
| 8.8. | Контрольная работа №7 «Решение уравнений и неравенств с двумя переменными» | 1 | 1 |
| 8.9. | Анализ контрольной работы №7 | 1 | 1 |
| 9. | Итоговое повторение курса алгебры и начал математического анализа | 12 | 12 |
|
| Итоговый тест | 1 | 1 |
-
ГРАФИК КОНТРОЛЬНЫХ РАБОТ
| Работа | Дата |
| 11/13 | 11/16 |
| Диагностическая контрольная работа | 09.09.13 | 09.09.13 |
| Контрольная работа №1 «Тригонометрические функции» | 11.10.13 | 11.10.13 |
| Контрольная работа №2 «Производная и ее геометрический смысл» | 26.11.13 | 26.11.13 |
| Контрольная работа №3 «Применение производной к исследованию функций» | 17.01.14 | 17.01.14 |
| Контрольная работа №4 «Интеграл» | 17.02.14 | 17.02.14 |
| Контрольная работа №5 «Элементы комбинаторики, статистики и теории вероятностей» | 08.04.14 | 08.04.14 |
| Контрольная работа №6 «Решение уравнений и неравенств с двумя переменными» | 28.04.14 | 28.04.14 |
| Итоговый тест | 20.05.14 | 20.05.14 |

 Получите свидетельство
Получите свидетельство Вход
Вход












 Рабочая программа по алгебре и началам математического анализа (11 класс) (0.16 MB)
Рабочая программа по алгебре и началам математического анализа (11 класс) (0.16 MB)
 0
0 3719
3719 1137
1137 Нравится
0
Нравится
0



