ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по предмету «Алгебра и начала анализа» составлена на основе Федерального компонента государственного образовательного стандарта среднего (полного) общего образования по математике (приказ Министерства образования Российской Федерации от 09.03.2004 г.), примерной программы среднего (полного) общего образования по математике (базовый уровень). Также использованы программы по алгебре и началам математического анализа (Алгебра и начала математического анализа. 10-11 классы: программы для общеобразовательных учреждений /сост. Т.А. Бурмистрова. – 2-е изд. – М.: Просвещение, 2010. – 159 с.).
Место предмета в учебном плане
В соответствии с учебным планом для общеобразовательных классов учебный предмет «Алгебра и начала анализа» изучается с 10 по 11 класс. Общее число часов – 103:
10 класс – 105 часов (3 часа в неделю);
11 класс – 104 часа (3 часа в неделю).
Так как учебным планом школы предусмотрено 35 учебных недель, на изучение данного предмета в рабочую программу добавлены 3 часа на тему «Повторение и решение задач» в 10 классе. Также из рабочей программы исключена тема «Алгебраические уравнения. Системы нелинейных уравнений».
| Разделы | Количество часов, предусмотренное авторами программы | Количество часов, предусмотренное рабочей программой |
| 10 класс Действительные числа | 11 | 11 |
| Степенная функция | 10 | 10 |
| Показательная функция | 10 | 10 |
| Логарифмическая функция | 14 | 14 |
| Алгебраические уравнения. Системы нелинейных уравнений | 13 | - |
| Тригонометрические формулы | 21 | 25 |
| Тригонометрические уравнения | 13 | 22 |
| Повторение и решение задач | 10 | 13 |
| Итого: | 102 | 105 |
| 11 класс Повторение курса алгебры и начал математического анализа 10 класс | 2 | 2 |
| Тригонометрические функции | 14 | 14 |
| Производная и ее геометрический смысл | 16 | 16 |
| Применение производной к исследованию функций | 16 | 16 |
| Интеграл | 13 | 13 |
| Комплексные числа | 15 | 15 |
| Элементы комбинаторики | 10 | 10 |
| Знакомство с вероятностью | 9 | 9 |
| Итоговое повторение курса алгебры и начал математического анализа | 7 | 7 |
| Итого: | 102 | 102 |
Общая характеристика учебного предмета
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа».
В рамках указанных содержательных линий решаются следующие задачи:
систематизация сведений о числах; изучение новых видов числовых выражений и формул;
совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
изучение свойств пространственных тел, формирование умения применять полученные знания для решения практических задач;
развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
знакомство с основными идеями и методами математического анализа.
Изучение математики на базовом уровне среднего (полного) общего образования направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Содержание и структура учебного предмета
АЛГЕБРА Корни и степени. Корень степени n1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем.
Логарифм. Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е.
Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень и операцию логарифмирования.
Основы тригонометрии. Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразования простейших тригонометрических выражений.
Простейшие тригонометрические уравнения и неравенства. Арксинус, арккосинус, арктангенс числа.
ФУНКЦИИ
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях.
Обратная функция. Область определения и область значений обратной функции. График обратной функции.
Степенная функция с натуральным показателем, её свойства и график.
Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций.
Тригонометрические функции, их свойства и графики; периодичность, основной период.
Показательная функция (экспонента), её свойства и график.
Логарифмическая функция, её свойства и график.
Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой 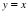 , растяжение и сжатие вдоль осей координат.
, растяжение и сжатие вдоль осей координат.
НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма.
Понятие о непрерывности функции.
Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков. Производные обратной функции и композиции данной функции с линейной.
Понятие об определенном интеграле как площади криволинейной трапеции. Первообразная. Формула Ньютона-Лейбница.
Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком. Примеры применения интеграла в физике и геометрии. Вторая производная и ее физический смысл.
УРАВНЕНИЯ И НЕРАВЕНСТВА
Решение рациональных, показательных, логарифмических уравнений и неравенств. Решение иррациональных и тригонометрических уравнений.
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной.
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ
Табличное и графическое представление данных. Числовые характеристики рядов данных.
Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.
Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов.
Основными видами деятельности учащихся по овладению прочными и осознанными знаниями в области математики являются:
построение и исследование математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
выполнение и самостоятельное составление алгоритмических предписаний и инструкций на математическом материале;
выполнение расчетов практического характера;
использование математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
самостоятельная работа с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
проведение доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
самостоятельная и коллективная деятельность, включение своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
Для достижения поставленных целей планируется использование следующих образовательных технологий:
а также различных методов и форм обучения:
словесных (объяснение, беседа, лекция), в которые входит работа с учебником
наглядных: метод иллюстраций, метод демонстраций (показ мультимедийных презентаций)
практических: устные, письменные и графические упражнения.
Межпредметные связи
Межпредметные связи в обучении математике являются важным средством достижения прикладной направленности обучения математике. Возможность подобных связей обусловлена тем, что в математике и смежных дисциплинах изучаются одноименные понятия (векторы, координаты, графики и функции, уравнения и т.д.), а математические средства выражения зависимостей между величинами (формулы, графики, таблицы, уравнения, неравенства) находят применение при изучении смежных дисциплин. Такое взаимное проникновение знаний и методов в различные учебные предметы имеет не только прикладную значимость, но и создает благоприятные условия для формирования научного мировоззрения.
Изучение всех предметов естественнонаучного цикла взаимосвязано с математикой. Математика дает учащимся систему знаний и умений, необходимых в повседневной жизни и трудовой деятельности человека, а также важных для изучения смежных дисциплин (физики, химии, черчения, трудового обучения, астрономии и др.).
При изучении физики целенаправленно применяются понятия пропорции, вектора, производной, функций, графиков и др.
Знания о процентах и умения решать уравнения используются в курсе химии.
Использование на уроках математики материала из художественных произведений, имеющего отношение к предмету, цитат известных людей о необходимости изучения математики позволяет внести в урок элементы занимательности и продемонстрировать связь математики с таким важным школьным предметом, как литература.
Из всех предметов общественно-гуманитарного цикла, изучаемых в школе, культурную значимость содержанию математики и ее методам исследования придает, несомненно, история.
Основными формами контроля являются
Урочные – традиционные:
Внеурочные
В 10 классе предусмотрено 9 тематических контрольных работ (включая стартовую и итоговую контрольные работы по текстам администрации), в 11 классе - 9 тематических контрольных работ (включая стартовую и итоговую контрольные работы по текстам администрации).
Результаты обучения
Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие основную школу, и достижение которых является обязательным условием положительной аттестации ученика за курс основной школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние две компоненты представлены отдельно по каждому из разделов, содержания.
СОДЕРЖАНИЕ КУРСА
10 класс ПРОВЕРИТЬ ТЕМЫ!!
(105 часов)
Действительные числа (11 часов)
Целые и рациональные числа. Действительные числа. Бесконечно убывающая геометрическая прогрессия и ее сумма. Арифметический корень натуральной степени. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Преобразования простейших выражений, включающих арифметические операции и операцию возведения в степень.
Основная цель - обобщить и систематизировать знания о действительных числах; сформировать понятие степени с действительным показателем; научить применять определения арифметического корня и степени, а также их свойства при выполнении вычислений и преобразовании выражений.
Необходимость расширения множества натуральных чисел до действительных мотивируется возможностью выполнять действия, обратные сложению, умножению и возведению в степень.
Рассмотренный в начале темы способ обращения бесконечной периодической десятичной дроби в обыкновенную обосновывается свойствами сходящихся числовых рядов, в частности, нахождением суммы бесконечно убывающей геометрической прогрессии.
Действия над иррациональными числами строго не определяются а заменяются действиями над их приближенными значениями - рациональными числами.
В связи с рассмотрением последовательных рациональных приближений иррационального числа, а затем и степени с иррациональным показателем на интуитивном уровне вводится понятие предела последовательности.
Арифметический корень натуральной степени n ≥ 2 из неотрицательного числа и его свойства излагаются традиционно. Учащиеся должны уметь вычислять значения корня с помощью определения и свойств и выполнять преобразования выражений, содержащих корни.
Степень с иррациональным показателем поясняется на конкретном примере. Здесь же формулируются свойства степени с действительным показателем, которые будут использоваться при решении уравнений, неравенств, исследовании функций.
Степенная функция (10 часов)
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Степенная функция с натуральным показателем, её свойства и график. Обратная функция. Равносильные уравнения и неравенства. Метод интервалов. Иррациональные уравнения. Иррациональные неравенства. Равносильность неравенств, систем.
Основная цель - обобщить и систематизировать известные из курса алгебры основной школы свойства функций; изучить свойства степенных функций с натуральным и целым показателями и научить применять их при решении уравнений и неравенств; сформировать понятие равносильности уравнений, неравенств, систем уравнений и неравенств.
Рассмотрение свойств степенных функций и их графиков проводится поэтапно, в зависимости от того, каким числом является показатель: 1) четным натуральным числом; 2) нечетным натуральным числом; 3) числом, противоположным четному числу; 4) числом, противоположным нечетному числу; 5) положительным нецелым числом; б) отрицательным нецелым числом (свойства функций в п. 5 и 6 изучать необязательно).
Обоснования свойств степенной функции не проводятся, они следуют из свойств степени с действительным показателем. Рассмотрение равносильности уравнений, неравенств и систем уравнений и свойств равносильности проводятся в связи с предстоящим изучением иррациональных уравнений и неравенств.
Основным методом решения иррациональных уравнений является возведение обеих частей уравнений в степень с целью перехода к рациональному уравнению-следствию данного.
Иррациональные неравенства не являются обязательными для изучения всеми учащимися. При их изучении основным способом решения является сведение неравенства к системе рациональных неравенств, равносильной данному неравенству.
Показательная функция (10 часов)
Показательная функция (экспонента), её свойства и график. Показательные уравнения. Решение показательных уравнений. Показательные неравенства. Системы показательных уравнений и неравенств.
Основная цель - изучить свойства показательной функции, научить решать показательные уравнения и неравенства, простейшие системы показательных уравнений и неравенств.
Свойства показательной функции полностью следуют из свойств степени с действительным показателем.
Решение большинства показательных уравнений и неравенств сводится к решению простейших.
Так как в ходе решения предлагаемых в этой теме показательных уравнений равносильность не нарушается, то проверка найденных корней необязательна. Здесь системы уравнений и неравенств решаются с помощью равносильных преобразований: подстановкой, сложением или умножением, заменой переменных и т. д.
Логарифмическая функция (14 часов)
Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени. Десятичный и натуральный логарифмы, число е. Свойства логарифмов. Формула перехода к новому основанию. Логарифмическая функция, её свойства и график. Логарифмические уравнения и неравенства. Решение логарифмических уравнений и неравенств.
Основная цель - сформировать понятие логарифма числа; научить применять свойства логарифмов при решении уравнений изучить свойства логарифмической функции и научить применять ее свойства при решении простейших логарифмических уравнений и неравенств.
До этой темы в курсе алгебры изучались такие функции, вычисление значений которых сводилось к четырем арифметическим действиям и возведению в степень. Для вычисления значений логарифмической функции нужно уметь находить логарифмы чисел, т. е. выполнять новое для учащихся действие - логарифмирование.
Доказательство свойств логарифма опирается на его определение. На практике рассматриваются логарифмы по различным основаниям, в частности по основанию 10 (десятичный логарифм) и по основанию е (натуральный логарифм), отсюда возникает необходимость формулы перехода от логарифма по одному основанию к логарифму по другому основанию. Так как на инженерном микрокалькуляторе есть клавиши 1g и ln, то для вычисления логарифма по основаниям, отличным от 10 и е, нужно применить формулу перехода.
Свойства логарифмической функции активно используются при решении.
Изучение свойств логарифмической функции проходит совместно с решением уравнений и неравенств.
При решении логарифмических уравнений и неравенств выполняются различные их преобразования. При этом часто нарушается равносильность. Поэтому при решении логарифмических уравнений необходима проверка найденных корней. Поэтому при решении логарифмических неравенств нужно следить за тем, чтобы равносильность не нарушалась, так как проверку решения неравенства осуществить сложно, а в ряде случаев невозможно.
Тригонометрические формулы (25 час)
Радианная мера угла. Поворот точки вокруг начала координат. Определение синуса, косинуса и тангенса угла. Синус, косинус, тангенс и котангенс числа. Знаки синуса, косинуса и тангенса. Зависимость между синусом, косинусом я тангенсом одного и того же угла. Основные тригонометрические тождества. Синус, косинус и тангенс углов и -. Синус, косинус и тангенс суммы и разности двух углов. Формулы сложения. Синус, косинус и тангенс двойного угла. Формулы половинного угла. Выражение тригонометрических функций через тангенс половинного аргумента. Формулы приведения. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Преобразования простейших тригонометрических выражений.
Основная цель - сформировать понятия синуса, косинуса, тангенса, котангенса числа; научить применять формулы тригонометрии для вычисления значений тригонометрических функций и выполнения преобразований тригонометрических выражений; научить решать простейшие тригонометрические уравнения siп х = а, соsх = а при а = 1, -1, 0.
Рассматривая определения синуса и косинуса действительного числа а, естественно решить самые простые уравнения, в которых требуется найти число а, если синус или косинус его известен, например уравнения sinα = 0, соsα = 1 и т. п. Поскольку для обозначения неизвестного по традиции используется буква х, то эти уравнения записывают как обычно: sin х = 0, соs х = 1 и т. п. Решения этих уравнений находятся с помощью единичной окружности.
Возможность выявления знаков синуса, косинуса и тангенса по четвертям является следствием симметрии точек единичной окружности относительно осей координат. Равенство соs(-α) = соsα следует из симметрии точек, соответствующих числам α и -α, относительно оси Ох.
Зависимость между синусом, косинусом, тангенсом и котангенсом одного и того же числа или угла следует из тригонометрической формы записи действительного числа и определения синуса и косинуса как координаты точки единичной окружности.
Формулы сложения доказываются для косинуса суммы или разности, все остальные формулы сложения получаются как следствия.
Формулы сложения являются основными формулами тригонометрии, так как все другие можно получить как следствия формулы двойного и половинного углов (не являются обязательными для изучения), формулы приведения, преобразования суммы и разности в произведение.
Тригонометрические уравнения (22 часа)
Уравнение cos х = а. Арккосинус числа. Уравнение sin х = а. Арксинус числа. Уравнение tg х = а. Арктангенс числа. Частные случаи решения уравнений cos х=а, sin х = а, tg х = а. Решение тригонометрических уравнений. Тригонометрические уравнения, сводящиеся к квадратным. Однородные тригонометрические уравнения. Уравнения, решаемые разложением левой части на множители. Примеры решения простейших тригонометрических неравенств
Основна цель - сформировать умение решать простейшие тригонометрические уравнения ознакомить с некоторыми приемами решения тригонометрических уравнений.
Как и при решении алгебраических, показательных и логарифмических уравнений, решение тригонометрических уравнений путем различных преобразований сводится к решению простейших: сох = а, sinх = а, tgх = а.
Рассмотрение простейших уравнений начинается с уравнения сох = а, так как формула его корней проще, чем формула корней уравнения siпх = а Решение более сложных тригонометрических уравнений, когда выполняются алгебраические и тригонометрические преобразования, сводится к решению простейших.
Рассматриваются следующие типы тригонометрических уравнений линейные относительно sin х, соs х или tg х; сводящиеся к квадратным и другим алгебраическим уравнениям после замены неизвестного; сводящиеся к простейшим тригонометрическим уравнениям после разложения на множители.
Повторение и решение задач (13 часов)
Действительные числа. Степенная функция, ее свойства. Иррациональные уравнения и неравенства. Показательная и логарифмическая функции. Логарифмические уравнения и неравенства. Формулы тригонометрии. Доказательство тождеств. Тригонометрические уравнения
Основная цель - восстановление в памяти учащихся основного материала, обобщение, уточнение систематизацию знаний по алгебре и началам математического анализа за курс 10 класса.
Повторение предлагается проводить по основным содержательно-методическим линиям и целесообразно выстроить в следующем порядке: вычисления и преобразования, уравнения и неравенства, функции, начала математического анализа.
Необходимым элементом уроков итогового повторения является самостоятельная работа учащихся. Она полезна как самим учащимся, так и учителю для осуществления обратной связи. Формы проведения самостоятельных работ разнообразны: от традиционной работы с двумя, тремя заданиями до тестов и работ в форме рабочей тетради с заполнением пробелов в приведенных рассуждениях.
11 КЛАСС
(102 часа)
Повторение курса алгебры и начал математического анализа 10 класс (2 часа)
Показательная и логарифмическая функции. Тригонометрические формулы и уравнения.
Основная цель - восстановление в памяти учащихся основного материала, обобщение, уточнение систематизацию знаний по алгебре и началам математического анализа за курс 10 класса.
Повторение предлагается проводить по основным содержательно-методическим линиям и целесообразно выстроить в следующем порядке: вычисления и преобразования, уравнения и неравенства, функции, начала математического анализа.
Необходимым элементом уроков итогового повторения является самостоятельная работа учащихся. Она полезна как самим учащимся, так и учителю для осуществления обратной связи. Формы проведения самостоятельных работ разнообразны: от традиционной работы с двумя, тремя заданиями до тестов и работ в форме рабочей тетради с заполнением пробелов в приведенных рассуждениях.
Тригонометрические функции (14 часов)
Тригонометрические функции. Область определения и множество значений тригонометрических функций. Свойства тригонометрических функций: четность, нечетность, периодичность, основной период. Тригонометрическая функция y = cos x, ее свойства и график. Преобразования графиков: параллельный перенос, симметрия относительно осей координат, растяжение и сжатие вдоль осей координат. Тригонометрическая функция y = sin x, ее свойства и график. Тригонометрическая функция у = tg x, ее свойства и график. Обратные тригонометрические функции. Преобразования графиков: симметрия относительно прямой у=х. Горизонтальные асимптоты графиков.
Основная цель: расширить и закрепить знания и умения, связанные с тождественными преобразованиями тригонометрических выражений; изучить свойства тригонометрических функций и познакомить учащихся с их графиками.
Изучение темы начинается с вводного повторения, в ходе которого напоминаются основные формулы тригонометрии, известные из курса алгебры, и выводятся некоторые новые формулы. От учащихся не требуется точного запоминания всех формул. Предполагается возможность использования различных справочных материалов: учебника, таблиц, справочников.
Особое внимание следует уделить работе с единичной окружностью. Она становится основой для определения синуса и косинуса числового аргумента и используется далее для вывода свойств тригонометрических функций и решения тригонометрических уравнений.
Систематизируются сведения о функциях и графиках, вводятся новые понятия, связанные с исследованием функций (экстремумы, периодичность), и общая схема исследования функций. В соответствии с этой общей схемой проводится исследование функций синус, косинус, тангенс и строятся их графики.
Производная и ее геометрический смысл (16 часов)
Производная функции, физический смысл производной. Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Непрерывность функции. Производная степенной функции. Правила дифференцирования суммы, разности, произведения, частного производных. Производная сложной функции. Производные основных элементарных функций. Производные обратной функции и композиции данной функции с линейной. Применение правил дифференцирования и формул для производных к решению задач. Уравнение касательной к графику функции. Геометрический смысл производной.
Основные цели: ввести понятие производной; научить находить производные функций в случаях, не требующих трудоемких выкладок.
При введении понятия производной и изучении ее свойств следует опираться на наглядно-интуитивные представления учащихся о приближении значений функции к некоторому числу, о приближении участка кривой к прямой линии и т. п.
Формирование понятия предела функции, а также умение воспроизводить доказательства каких-либо теорем в данном разделе не предусматриваются. В качестве примера вывода правил нахождения производных в классе рассматривается только теорема о производной суммы, все остальные теоремы раздела принимаются без доказательства. Важно отработать достаточно свободное умение применять эти теоремы в несложных случаях.
В ходе решения задач на применение формулы производной сложной функции можно ограничиться случаем f(kx + b): именно этот случай необходим далее.
Применение производной к исследованию функций (16 часов)
Возрастание и убывание функций. Промежутки возрастания и убывания. Точки экстремума (локального максимума и минимума). Применение производной к исследованию функций и построению графиков функций. Построение графиков функций. Преобразования графиков: симметрия относительно осей координат и начала координат. Наибольшее и наименьшее значения функции. Примеры функциональных зависимостей в реальных процессах и явлениях. Длина окружности и площадь круга как пределы последовательностей. Вторая производная и ее физический смысл.
Основная цель: ознакомить с простейшими методами дифференциального исчисления; выработать умение применять их для исследования функций и построения графиков.
Опора на геометрический и механический смысл производной делает интуитивно ясными критерии возрастания и убывания функций, признаки максимума и минимума.
Основное внимание должно быть уделено разнообразным задачам, связанным с использованием производной для исследования функций. Остальной материал (применение производной к приближенным вычислениям, производная в физике и технике) дается в ознакомительном плане.
Первообразная. Правила нахождения первообразной. Площадь криволинейной трапеции и интеграл. Формула Ньютона-Лейбница. Вычисление интегралов. Понятие об определенном интеграле как площади криволинейной трапеции. Вычисление площадей с помощью интегралов. Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком. Примеры применения интеграла в физике и геометрии.
Основные цели: ознакомить с интегрированием как операцией, обратной дифференцированию; показать применение интеграла к решению геометрических задач.
Задача отработки навыков нахождения первообразных не ставится, упражнения сводятся к простому применению таблиц и правил нахождения первообразных.
Интеграл вводится на основе рассмотрения задачи о площади криволинейной трапеции и построения интегральных сумм. Формула Ньютона - Лейбница вводится на основе наглядных представлений.
В качестве иллюстрации применения интеграла рассматриваются только задачи о вычислении площадей и объемов. Следует учесть, что формула объема шара выводится при изучении данной темы и используется затем в курсе геометрии.
Материал, касающийся работы переменной силы и нахождения центра масс, не является обязательным.
При изучении темы целесообразно широко применять графические иллюстрации.
Комплексные числа (15 часов)
Табличное и графическое представление данных. Числовые характеристики рядов данных. Определение комплексных чисел. Сложение и умножение комплексных чисел. Модуль комплексного числа. Свойства модуля и аргумента комплексного числа Вычитание и деление комплексных чисел. Геометрическая интерпретация комплексного числа. Тригонометрическая форма комплексного числа. Квадратное уравнение с комплексным неизвестным. Примеры решения алгебраических уравнений. Поочередный и одновременный выбор нескольких элементов из конечного множества.
Основные цели - научить представлять комплексное число в алгебраической и тригонометрической формах; изображать число на комплексной плоскости; научить выполнять операции сложения, вычитания, умножения и деления чисел, записанных в алгебраической форме, операции умножения и деления чисел, представленных в тригонометрической форме.
Комплексные числа вводятся либо как упорядоченная пара чисел, либо как выражение a+bi, где a и b - действительные числа, i - некоторый символ, такой, что i2 =-1. Затем формулируются правила, устанавливающие равенство комплексных чисел, вводятся
числа, соответствующие привычным для школьников нулю и единице, изучаются правила арифметических действий над комплексными числами.
Тригонометрическая интерпретация комплексного числа позволяет решать алгебраические уравнения (в частности, квадратные) в поле комплексных чисел и осознанно воспринимать основную теорему алгебры, которая формулируется в конце темы
Элементы комбинаторики (10 часов)
Комбинаторные задачи. Перестановки. Размещения. Сочетания и их свойства. Формулы числа перестановок, сочетаний, размещений. Перестановки. Размещения. Сочетания и их свойства. Формулы числа перестановок, сочетаний, размещений. Биномиальная формула Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.
Основные цели - ознакомление с основными формулами комбинаторики и их применением при решении задач; формирование элементов комбинаторного мышления.
Основой при выводе формул числа перестановок и размещений является правило умножения, понимание которого формируется при решении различных прикладных задач. Свойства числа сочетаний доказываются и затем применяются при организации и исследовании треугольника Паскаля.
Рекомендуется дополнять комбинаторные задачи учебника аналогичными по конструкции, но использующими фабулу, соответствующую профилю обучения.
Знакомство с вероятностью (9 часов)
Вероятность события. Элементарные и сложные события. Сложение вероятностей. Рассмотрение случаев и вероятность суммы несовместных событий. Вероятность противоположного события. Условная вероятность. Понятие о независимости событий. Вероятность произведения независимых событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов.
Основная цель - формирование умения находить вероятность случайных событий в простейших случаях, используя классическое определение вероятности и применяя при необходимости формулы комбинаторики.
Классическое определение вероятности случайного события вводится после рассмотрения относительной частоты (статистической вероятности) события «выпал орел» в опыте с подбрасыванием монеты. Возможна организация реальных экспериментов с целью установления того факта, что при увеличении числа экспериментов (например, при подбрасывании монеты или кости) относительная частота рассматриваемого события «все более приближается» к некоторому числу, являющемуся вероятностью события. Такая работа поможет осознать и понятие элементарного события.
При решении задач на подсчет вероятности с использованием определения этого понятия многим учащимся проще сначала находить число всех элементарных исходов события, а затем уже число благоприятствующих исходов.
Вводятся понятия достоверных и невозможных событий, устанавливается вероятность каждого из них. Теме «Сложение вероятностей» в классах любого профиля достаточно уделить один урок.
Понятие независимости событий вводится после знакомства с понятием условной вероятности. Задачи нахождения вероятности произведения независимых событий формулируются в основном для ситуации, когда независимость рассматриваемых событий очевидна.
Итоговое повторение курса алгебры и начал математического анализа (7 часов)
Числа и алгебраические преобразования. Решение уравнений и неравенств. Решение систем уравнений и неравенств. Текстовые задачи. Функции и их графики. Производная и интеграл
Цели: повторить и обобщить навыки решения основных типов задач по следующим темам: числа и алгебраические преобразования, решение уравнений, решение неравенств, решение систем уравнений и неравенств, функции и их графики, производная функции и ее применение к решению задач, первообразная, элементы математической статистики, комбинаторики и теории вероятностей.
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ
В результате изучения математики на базовом уровне ученик должен
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира;
Алгебра
уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Начала математического анализа
уметь
вычислять производные и первообразные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения прикладных задач, в том числе социально-экономи-ческих и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
составлять уравнения и неравенства по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Элементы комбинаторики, статистики и теории вероятностей
уметь
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
анализа реальных числовых данных, представленных в виде диаграмм, графиков;
анализа информации статистического характера.
ПЕРЕЧЕНЬ УЧЕБНО-МЕТОДИЧЕСКОГО ОБЕСПЕЧЕНИЯ
а) учебная и методическая литература
Алгебра и начала математического анализа. 10-11 классы. Программа общеобразовательных учреждений / сост. Т.А. Бурмистрова. – М.: Просвещение, 2010. – 159 с.
Алимов Ш.А. Алгебра и начала математического анализа: Учеб. для 10–11 кл. общеобразоват. учреждений /Ш.А. Алимов, Ю.М. Колягин, Ю. В. Сидоров и др.; – М.: Просвещение, 2014. – 463 с.
Алимов Ш.А. Алгебра: учеб. для 9 кл. общеобразовательных учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. – М.: Просвещение, 2013.
Александрова Л. А.. Алгебра и начала анализа. Самостоятельные работы - М.: Мнемозина 2013
Глизбург В. И. Алгебра и начала анализа 10 класс. Контрольные работы. Базовый уровень - М.: Мнемозина, 2013
Глизбург В. И. Алгебра и начала анализа 11 класс. Контрольные работы. Базовый уровень - М.: Мнемозина, 2013
Звавич Л.И. и др. Алгебра и начала анализа: 3600 задач для школьников и поступающих в вузы. М.: Дрофа, 2012.
Мордкович А.Г. Алгебра и начала математического анализа 10-11 классы. Часть 1. Учебник для учащихся общеобразовательных учреждений (базовый уровень). М.: «Мнемозина», 2013.
Мордкович А.Г. и др. Алгебра и начала математического анализа 10-11 классы. Часть 2. Задачник для учащихся общеобразовательных учреждений (базовый уровень). М.: «Мнемозина», 2013.
Решение задач и выполнение заданий по математике с комментариями и ответами для подготовки к ЕГЭ / Сост. В.Н. Студенецкая, З.С. Гребнева. – Волгоград: Учитель, 2014. – 228 с.
Рурукин А.Н. Поурочные разработки по алгебре и началам анализа 10 класс. – М.: ВАКО, 2011. – 352 с.
Рурукин А.Н., Бровкова Е.В., Лупенко Г.В. и др. Поурочные разработки по алгебре и началам анализа 11 класс. – М.: ВАКО, 2014. – 336 с.
Сканави М.И. Сборник задач по математике для поступающих в вузы. Книга 1. Алгебра. М.: ОНИКС 21 век, Мир и образование, 2013.
б) адреса сайтов в Интернете:
1000zadach.info - интернет-сборник задач по школьному курсу математики.
http://mat.1september.ru - Газета "Математика" Издательского дома «Первое сентября»
http://comp-science.narod.ru - Дидактические материалы по информатике и математике
http://methmath.chat.ru - Методика преподавания математики
http://www.math.ru - Math.ru: Математика и образование
http://www.math-on-line.com - Занимательная математика — школьникам (олимпиады, игры, конкурсы по математике)
Интернет-ресурс «Единая коллекция цифровых образовательных ресурсов». – http://school-collection.edu.ru.
Интернет-ресурс «Открытая математика. Стереометрия». – www.college.ru.
Интернет-ресурс «Открытый банк заданий по математике». – http://mathege.ru:8080/or/ege/Main.
в) программные средства
- система компьютерного черчения;
- растровый графический редактор Paint;
- интерактивные компьютерные модели:
Открытая математика. Функции и графики;
Открытая математика. Планиметрия;
Открытая математика. Стереометрия;
- приложение разработки презентаций MS PowerPoint;
- электронные таблицы MS Excel;
- текстовый редактор MS Word;
- калькуляторы NumLock Calculator и Wise Calculator.

 Получите свидетельство
Получите свидетельство Вход
Вход



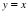 , растяжение и сжатие вдоль осей координат.
, растяжение и сжатие вдоль осей координат. 








 Рабочая программа по предмету «Алгебра и начала анализа» (10-11 классы) (76.67 КB)
Рабочая программа по предмету «Алгебра и начала анализа» (10-11 классы) (76.67 КB)
 0
0 930
930 235
235 Нравится
0
Нравится
0


