9Муниципальное бюджетное общеобразовательное учреждение
«Бетькинская средняя общеобразовательная школа»
Тукаевского муниципального района
Республики Татарстан
УТВЕРЖДЕНО
протоколом педагогического совета
от _27. 08_2014_ г. № __1__
Директор МБОУ « Бетькинская СОШ»
____________ Даутова З.И. _
подпись Ф.И.О.
Введено приказом №_____
от ___ ________ 2014_ г.
РАБОЧАЯ ПРОГРАММА
ПО ПРЕДМЕТУ МАТЕМАТИКА_
ДЛЯ _10_ КЛАССА (кол-во часов в неделю -6, в год-210)
СоставительГаляутдиноваГульфияАсватовна, учитель математики
СОГЛАСОВАНО
Зам.директора ____________ Шагимарданова Р. А.
подпись Ф.И.О.
РАССМОТРЕНО
на заседании МО, протокол от 27. 08. 2014__ г. № _1_
Руководитель МО ___________ Галяутдинова Г.А.
подпись Ф.И.О.
2014 – 2015 учебный год
2.Пояснительная записка
Рабочая программа по математике в 10 классе составлена на основе
-федерального компонента государственного стандарта среднего (полного) общего образования (приказ МОиН РФ от 05.03.2004г. № 1089),
-примерных программ по математике (составители:Э.Д.Днепров, А.Г.Аркадьев; М., Дрофа, 2007),
-программы для общеобразовательных учреждений. Алгебра и начала анализа. 10-11 классы. / Сост.Т.А.Бурмистрова, М.Просвещение, 2008г.)
-программы для общеобразовательных учреждений. Геометрия 10-11 классы. / сост.Т.А.Бурмистрова, М.Просвещение, 2008г.)
-Письма МО и Н РФ «О преподавании математики» №7294/ 9 от 29.09.09;
-федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2013-2014 учебный год ( Алгебра и начала анализа: учеб.для 10 кл. общеобразоват. Учреждений / С.М. Никольский и др.- М.: Просвещение, 2010; Геометрия. Учебник для 10-11 классов авторы: Л.С. Атанасян, Ф.Б. Бутузов, С.Б. Кадомцев и др. М: Просвещение, 2010.
- с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования;
- учебного плана МБОУ «Бетькинскаясош» 2014-2015года.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса.
Рабочая программа выполняет две основные функции:
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Цели и задачи изучения математики в 10 классе:
Изучение математики в старшей школе на профильном уровне направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитиелогического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Место предмета в учебном плане МБОУ «Бетькинскаясош».
Согласно Федеральному базисному учебному плану на изучение математики в 10 классе отводится не менее 210 часов из расчета 6 ч в неделю. Из них на геометрию 2 часа в неделю и 4 часа на алгебру и начала анализа. При этом предполагается построение курса в форме последовательности тематических блоков с чередованием материала по алгебре, анализу и геометрии.
Профильный уровень (6 часов в неделю) содержательно превышает базовый уровень и приближается к углубленному курсу преподавания математики за счет введения элементов теории многочленов, расширения курса геометрии.
Количество учебных часов в учебном плане МБОУ «Бетькинскаясош»:
В год -210 часов (6 часов в неделю)
В том числе: контрольных работ-12, включая итоговую контрольную работу.
Формы промежуточной и итоговой аттестации:
Промежуточная аттестация проводится в форме тестов, контрольных, самостоятельных работ, зачетов. Итоговая аттестация предусмотрена в виде разно уровневого теста (2 часа) в форме ЕГЭ.
Уровень обучения – профильный.
Срок реализации рабочей учебной программы – один учебный год.
В данном классе ведущими методами обучения предмету являются: объяснительно-иллюстративный, репродуктивный, частично-поисковый. На уроках используются элементы следующих технологий: личностно ориентированное обучение, обучение с применением опорных схем, ИКТ.
С целью закрепления и углубления знаний обучающихся по основным разделам программы школьный компонент (35 ч.) использован на следующие уроки:
* Действительные числа – 5 часов.
* Рациональные уравнения и неравенства – 4 часа.
* Корень степени n – 4 часа.
* Степень положительного числа – 4 часа.
* Показательные и логарифмические уравнения и неравенства – 4 часа.
* Тангенс и котангенс угла – 2 часа.
* Формулы сложения – 1 час.
* Тригонометрические функции числового аргумента – 1 час.
* Тригонометрические уравнения и неравенства – 4 часа. * Вероятность события – 2 часа.
* Частота. Условная вероятность – 2 часа.
* Повторение – 2 часа.
В профильном курсе содержание образования развивается в следующих направлениях:
• систематизация сведений о числах; формирование представлений о расширении числовых множеств как способе построения нового математического аппарата для решения задач окружающего мира и внутренних задач математики; совершенствование техники вычислений;
• развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств, систем;
• систематизация и расширение сведений о функциях, совершенствование графических умений; знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи;
• расширение системы сведений о свойствах плоских фигур, систематическое изучение свойств пространственных тел, развитие представлений о геометрических измерениях;
• развитие представлений о вероятностно-статистических закономерностях в окружающем мире;
• совершенствование математического развития до уровня, позволяющего свободно применять изученные факты и методы при решении задач из различных разделов курса, а также использовать их в нестандартных ситуациях;
• формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
Содержание программы учебного курса
1. Действительные числа и элементы комбинаторики (12ч.)
Понятие натурального числа. Множества чисел. Свойства действительных чисел. Метод математической индукции. Перестановки. Размещения. Сочетания. Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Доказательства неравенств. Неравенство о среднем арифметическом и среднем геометрическом двух чисел. Делимость целых чисел. Деление с остатком. Сравнения по модулю m . Задачи с целочисленными неизвестными.
Основная цель — систематизировать известные и изучить новые сведения о действительных числах.
При изучении первой темы сначала проводится повторение изученного в основной школе по теме «Действительные числа». Затем изучаются перестановки, размещения и сочетания. Здесь важно понять разницу между ними и научиться применять их при решении задач.
Необходимо овладеть методом математической индукции и научиться применять его при решении задач. Важным элементом обучения является овладение методами доказательства числовых неравенств. Делимость чисел изучается сначала для натуральных чисел, а затем для целых чисел. Это приводит к новому понятию: сравнению чисел по модулю. Приводится решение многочисленных задач с помощью сравнения по модулю. Наконец, рассматриваются разнообразные диофантовы уравнения.
2. Рациональные уравнения и неравенства (18ч.)
Рациональные выражения. Формулы бинома Ньютона, суммы и разности степеней. Делимость многочленов. Деление многочленов с остатком. Рациональные корни многочленов с целыми коэффициентами. Схема Горнера. Теорема Безу. Число корней многочлена. Многочлены от двух переменных. Формулы сокращенного умножения для старших степеней. Бином Ньютона.Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля. Многочлены от нескольких переменных, симметрические многочлены.Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение систем уравнений с двумя неизвестными (простейшие типы). Решение систем неравенств с одной переменной.Рациональные уравнения. Системы рациональных уравнений. Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем. Метод интервалов решения неравенств. Рациональные неравенства. Нестрогие неравенства. Системы рациональных неравенств. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
Основная цель — сформировать умения решать рациональные уравнения и неравенства. При изучении этой темы сначала повторяются известные из основной школы сведения о рациональных выражениях. Затем эти сведения дополняются формулами бинома Ньютона, суммы и разности одинаковых натуральных степеней. Повторяются старые и приводятся новые способы решения рациональных уравнений и систем рациональных уравнений. Рассматривается метод интервалов решения неравенств вида (х – х1) ... (х - хп) 0 или (х – х1) ... (х - хп) 0. (*)
Он основан на свойстве двучлена х - а обращаться в нуль только в одной точке а, принимать положительные значения для каждого х а и отрицательные значения для каждого х Решение строгих рациональных неравенств сводится к решению неравенств вида (*).
Нестрогие неравенства вводятся только после рассмотрения всех строгих неравенств. Для решения нестрогого неравенства надо решить уравнение и строгое неравенство, а затем объединить все найденные решения. После этого рассматриваются системы рациональных неравенств.
Решению рациональных уравнений и неравенств помогает метод нахождения рациональных корней многочлена Рп(х) степени п≥ 3, изучение деления многочленов и теоремы Безу.м
3. Корень степени п(12ч.)
Понятия функции и ее графика. Функция у = хп. Степенная функция с натуральным показателем, ее свойства и график.Понятие корня степени п. Корни четной и нечетной степеней. Арифметический корень. Свойства корней степени п. Функция у= .Корень степени n1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Корень степени n из натурального числа.
.Корень степени n1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Корень степени n из натурального числа.
Основная цель — освоить понятия корня степени пи арифметического корня; выработать умение преобразовывать выражения, содержащие корни степени п.
При изучении этой темы сначала напоминаются определения функции и ее графика, свойства функции у = хп. Существование двух корней четной степени из положительного числа и одного корня нечетной степени из любого действительного числа показывается их применению к преобразованию выражений, содержащих корни.
4. Степень положительного числа (13ч.)
Понятие и свойства степени с рациональным показателем. Понятие о пределе последовательности.Существование предела монотонной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма. Теоремы о пределах последовательностей. Переход к пределам в неравенствах. Свойства пределов. Бесконечно убывающая геометрическая прогрессия. Число е. Понятие степени с иррациональным показателем. Показательная функция (экспонента), ее свойства и график.
Основная цель — усвоить понятия рациональной и иррациональной степеней положительного числа и показательной функции.
Сначала вводятся понятие рациональной степени положительного числа и изучаются ее свойства. Затем вводится понятие предела последовательности и с его помощью находится сумма бесконечно убывающей геометрической прогрессии. Степень с иррациональным показателем определяется с использованием предела последовательности, после чего вводится показательная функция, и изучаются ее свойства и график.
5. Логарифмы (6ч.)
Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы,число е. Логарифмическая функция, ее свойства и график Преобразования выражений, включающих арифметические операции, а также операции возведения в степень и логарифмирования.
Основная цель — освоить понятия логарифма и логарифмической функции, выработать умение преобразовывать выражения, содержащие логарифмы.
Сначала вводятся понятия логарифма, десятичного и натурального логарифмов, изучаются свойства логарифмов. Затем рассматривается логарифмическая функция, и изучаются ее свойства и график.
6. Показательные и логарифмические уравнения и неравенства (11ч.)
Решение простейших показательных и логарифмических уравнений и неравенств. Уравнения, сводящиеся к простейшим заменой неизвестного.. Неравенства, сводящиеся к простейшим заменой неизвестного.
Основная цель — сформировать умение решать показательные и логарифмические уравнения и неравенства.
Сначала изучаются простейшие показательные уравнения, находятся их решения. Затем аналогично изучаются простейшие логарифмические уравнения. Далее рассматриваются уравнения, решение которых (после введения нового неизвестного tи решения получившегося рационального уравнения относительно tсводится к решению простейшего показательного (или логарифмического) уравнения.
По такой же схеме изучаются неравенства: сначала простейшие показательные, затем простейшие логарифмические, и наконец, неравенства, сводящиеся к простейшим заменой неизвестного.
7. Синус и косинус угла (7ч.)
Синус, косинус произвольного угла. Радианная мера угла. Синус, косинус числа. Основные тригонометрические тождества.Арксинус, арккосинус числа.
Основная цель — освоить понятия синуса и косинуса произвольного угла, изучить свойства функций угла: sinαиcosα.
Используя язык механики, вводится понятие угла как результата поворота вектора. Затем вводятся его градусная и радианная меры. С использованием единичной окружности вводятся понятия синуса и косинуса угла. Изучаются свойства функций sinαи cosα, как функций угла α, доказываются основные формулы для них.
Вводятся понятия арксинуса и арккосинуса числа и с их помощью решаются задачи на нахождение всех углов, для каждого из которых sinα (илиcosα) равен (больше или меньше) некоторого числа.
8. Тангенс и котангенс угла (6ч.)
. Тангенс, котангенс произвольного угла. Радианная мера угла. Тангенс и котангенс числа. Основные тригонометрические тождества.Арктангенс, арккотангенс числа
Основная цель — освоить понятия тангенса и котангенса произвольного угла, изучить свойства функций угла: tgαиctgα.
Тангенс и котангенс угла α определяются как с помощью отношений sinαи cosα, так и с помощью осей тангенса и котангенса. Изучаются свойства функций tgαиctgα как функций угла α, доказываются основные формулы для них.
Вводятся понятия арктангенса и арккотангенса числа и с их помощью решаются задачи на нахождение всех углов, для каждого из которых tgα(илиctgα) равен (больше или меньше) некоторого числа.
9. Формулы сложения (11ч.)
Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразования тригонометрических выражений
Основная цель — освоить формулы косинуса и синуса суммы и разности двух углов, выработать умение выполнять тождественные преобразования тригонометрических выражений с использованием выведенных формул.
Сначала с помощью скалярного произведения векторов доказывается формула косинуса разности двух углов. Затем с помощью свойств синуса и косинуса угла и доказанной формулы выводятся все перечисленные формулы. Используя доказанные формулы, выводятся формулы для синусов и косинусов двойных и половинных углов, а также для произведения синусов и косинусов углов. Наконец, выводятся формулы для тангенса суммы (разности) двух углов тангенса двойного и половинного углов, для выражения синуса, косинуса и тангенса угла через тангенс половинного угла.
10. Тригонометрические функции числового аргумента (9ч.)
Функции у = sinх,у =cos х, у = tg х, у= ctg х Тригонометрические функции, их свойства и графики, периодичность, основной период. Основная цель — изучить свойства основных тригонометрических функций и их графиков.
Сначала говорится о том, что хотя функция может выражать зависимость между разными физическими величинами, но в математике принято рассматривать функции  как функции числа. Поэтому здесь и рассматриваются тригонометрические функции числового аргумента, их основные свойства. С использованием свойств тригонометрических функций строятся их графики.
как функции числа. Поэтому здесь и рассматриваются тригонометрические функции числового аргумента, их основные свойства. С использованием свойств тригонометрических функций строятся их графики.
При изучении этой темы вводится понятие периодической функции и ее главного периода, доказывается, что главный период функций у = sin х и у =cos х: есть число 2π, а главный период функций у = tg х и у= ctg х есть число π.
11. Тригонометрические уравнения и неравенства (12ч.)
Простейшие тригонометрические уравнения. Решения тригонометрических уравнений. Простейшие тригонометрические неравенства.
Основная цель — сформировать умение решать тригонометрические уравнения и неравенства.
Сначала с опорой на умение решать задачи на нахождение всех углов х таких, что f(х) = а, где f(х) — одна из основных тригонометрических функций (sin х, cos х , tg х ,ctg х), рассматривается решение простейших тригонометрических уравнений. Затем рассматриваются уравнения, которые (после введения нового неизвестного tи решения получившегося рационального уравнения относительно t) сводятся к решению простейшего тригонометрического уравнения. Рассматриваются способы решения тригонометрических уравнений с помощью основных тригонометрических формул и, наконец, рассматриваются однородные тригонометрические уравнения.
С опорой на умение решать задачи на нахождение всех углов х таких, что f(х) а, или f(х) f(х) — одна из основных тригонометрических функций, рассматривается решение простейших тригонометрических неравенств. Затем рассматриваются неравенства, которые (после введения нового неизвестного tи решения получившегося рационального неравенства относительно t} сводятся к решению простейших тригонометрических неравенств.
12. Элементы теории вероятности (8ч.)
Числовые характеристики рядов данных.Поочередный и одновременный выбор нескольких элементов из конечного множества. Понятие и свойства вероятности события. Относительная частота события. Условная вероятность. Независимые события.
Основная цель — овладеть классическим понятием вероятности события, понятиями частоты события и условной вероятности события, независимых событий; изучить его свойства и научиться применять их при решении несложных задач.
Сначала рассматриваются опыты, результаты которых называют событиями. Определяется вероятность события. Рассматриваются примеры вычисления вероятности события. Затем вводятся понятия объединения (суммы), пересечения (произведения) событий и рассматриваются примеры на применение этих понятий.
Сначала вводится понятие относительной частоты события и статистической устойчивости относительных частот. Затем рассматривается вопрос о разных способах определения вероятности: классическом, статистическом, аксиоматическом. Вводятся понятия условной вероятности и независимых событий, рассматриваются примеры на применение этих понятий
ГЕОМЕТРИЯ
Аксиомы стереометрии и их следствия (15ч.)
Свойство биссектрисы угла треугольника. Решение треугольников. Вычисление биссектрис, медиан, высот, радиусов вписанной и описанной окружностей. Формулы площади треугольника: формула Герона, выражение площади треугольника через радиус вписанной и описанной окружностей.
Вычисление углов с вершиной внутри и вне круга, угла между хордой и касательной.
Теорема о произведении отрезков хорд. Теорема о касательной и секущей. Теорема о сумме квадратов сторон и диагоналей параллелограмма
Вписанные и описанные многоугольники. Свойства и признаки вписанных и описанных четырехугольников.
Геометрические места точек.
Решение задач с помощью геометрических преобразований и геометрических мест.
Теорема Чевы и теорема Менелая.
Эллипс, гипербола, парабола как геометрические места точек. Неразрешимость классических задач на построение.
Основная цель - сформировать представления учащихся об основных понятиях и аксиомах стереометрии, их использовании при решении стандартных задач логического характера, а также об изображениях точек, прямых и плоскостей на проекционном чертеже при различном их взаимном расположении в пространстве.
Прямые и плоскости в пространстве (33ч.)
Основные понятия стереометрии (точка, прямая, плоскость, пространство). Понятие об аксиоматическом способе построения геометрии.
Пересекающиеся, параллельные и скрещивающиеся прямые. Угол между прямыми в пространстве. Перпендикулярность прямых.Параллельность и перпендикулярность прямой и плоскости, признаки и свойства. Теорема о трех перпендикулярах. Перпендикуляр и наклонная к плоскости. Угол между прямой и плоскостью. Параллельность плоскостей, перпендикулярность плоскостей, признаки и свойства. Двугранный угол, линейный угол двугранного угла. Расстояния от точки до плоскости. Расстояние от прямой до плоскости. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми. Параллельное проектирование. Ортогональное проектирование. Площадь ортогональной проекции многоугольника. Изображение пространственных фигур. Центральное проектирование.
Основная цель – дать учащимся систематические сведения о параллельности и перпендикулярности прямых и плоскостей в пространстве; ввести понятие углов между прямыми и плоскостями, между плоскостями. В ходе изучения темы обобщаются и систематизируются знания учащихся о перпендикулярности прямых, перпендикуляре и наклонных, известные им из курса планиметрии. При изучении материала следует обратить внимание на часто используемый метод доказательства от противного, знакомый учащимся из курса планиметрии.
Многогранники (14ч.)
Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники.Теорема Эйлера.
Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб.
Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида.
Симметрии в кубе, в параллелепипеде, в призме и пирамиде.
Понятие о симметрии в пространстве (центральная, осевая, зеркальная).
Сечения многогранников. Построение сечений.
Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Основная цель – дать учащимся систематические сведения об основных видах многогранников. Изучение многогранников нужно вести на наглядной основе, опираясь на объекты природы, предметы окружающей действительности.
Повторение (23 ч).
4. Требования к уровню подготовки выпускников
В результате изучения математики на профильном уровне в старшей школе ученик должен
Знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
возможности геометрического языка как средства описания свойств реальных предметов и их взаимного расположения;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностный характер различных процессов и закономерностей окружающего мира.
Числовые и буквенные выражения
Уметь:
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
*практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, при необходимости используя справочные материалы и простейшие вычислительные устройства.
Функции и графики
Уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Начала математического анализа
Уметь
находить сумму бесконечно убывающей геометрический прогрессии;
вычислять производные и первообразные элементарных функций, применяя правила вычисления производных и первообразных, используя справочные материалы;
исследовать функции и строить их графики с помощью производной,;
решать задачи с применением уравнения касательной к графику функции;
решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
вычислять площадь криволинейной трапеции;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа.
Уравнения и неравенства
Уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
доказывать несложные неравенства;
решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учетом ограничений условия задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Элементы комбинаторики, статистики и теории вероятностей
Уметь:
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
вычислять, в простейших случаях, вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
Геометрия
Уметь:
соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями; различать и анализировать взаимное расположение фигур;
изображать геометрические фигуры и тела, выполнять чертеж по условию задачи;
решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат;
проводить доказательные рассуждения при решении задач, доказывать основные теоремы курса;
вычислять линейные элементы и углы в пространственных конфигурациях, объемы и площади поверхностей пространственных тел и их простейших комбинаций;
применять координатно-векторный метод для вычисления отношений, расстояний и углов;
строить сечения многогранников и изображать сечения тел вращения;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства
Общеучебные умения, навыки и способы деятельности
В ходе изучения математики в профильном курсе старшей школы учащиеся продолжают овладение разнообразными способами деятельности, приобретают и совершенствуют опыт:
проведения доказательных рассуждений, логического обоснования выводов, использования различных языков математики для иллюстрации, интерпретации, аргументации и доказательства;
решения широкого класса задач из различных разделов курса, поисковой и творческой деятельности при решении задач повышенной сложности и нетиповых задач;
планирования и осуществления алгоритмической деятельности: выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; использования и самостоятельного составления формул на основе обобщения частных случаев и результатов эксперимента; выполнения расчетов практического характера;
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин и реальной жизни; проверки и оценки результатов своей работы, соотнесения их с поставленной задачей, с личным жизненным опытом;
самостоятельной работы с источниками информации, анализа, обобщения и систематизации полученной информации, интегрирования ее в личный опыт.
Результаты обучения
Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все выпускники, изучавшие курс математики по профильному уровню, и достижение которых является обязательным условием положительной аттестации ученика за курс средней (полной) школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние две компоненты представлены отдельно по каждому из разделов, содержания.
УТВЕРЖДАЮ
Директор МБОУ «_ Бетькинская СОШ_»
____________ __ Даутоваз.И.
подпись Ф.И.О.
Календарно-тематический план
ГаляутдиноваГульфияАсватовна
учителя математики на 2014-2015 учебный год
План составлен на основе федерального компонента государственного стандарта среднего (полного) общего образования, на основе сборника нормативных документов. Математика / сост. Э.Д.Днепров, А.Г.Аркадьев .- М.: Дрофа, 2010, и согласно учебному плану МБОУ « Бетькинская средняя общеобразовательная школа».
| Предмет | Класс | Всего кол-во часов | Кол-во часов в неделю | Количество | Название, автор учебника, издательство, год издания, уровень. |
| Контрольных работ | зачетов | Тестовых заданий |
| математика | 10 | 210 | 6 | 12 | 3 | 10 | Учебник «Алгебра и начала анализа 10 класс» авторы С.М.Никольский и др. - М.: Просвещение, 2010 г., рекомендовано Министерством образования и науки РФ Учебник «Геометрия, 10-11» авторы: Л.С. Атанасян, В.Ф. Бутузов и др., - М.: Просвещение, 2010 г. рекомендован министерством образования РФ. |
Методическая тема на 2014-15 учебный год
| Районная | Школьная | Учителя |
| Повышение качества естественно-математического образования через эффективное использование современных технологий и внедрение новых обучающих структур в практику обучения и воспитания. | Использование современных образовательных технологий и внедрение новых обучающих структур для повышения эффективности качества образования. | Использование ИКТ на уроках математики с целью повышения мотивации учащихся и повышения качества знаний. |
Календарно – тематическое планирование по математике
10 класс
| № п/п | Изучаемый раздел, тема учебного материала | Кол-во часов | Календарные сроки по плану | Фактические сроки проведения урока | Планируемые результаты | Контрольно-измерительные материалы |
| Знания | Умения | Общие учебные умения, навыки и способы деятельности |
|
| I полугодие | 95 |
|
|
.Знать определение понятие натурального числа. Множества чисел. Свойства действительных чисел. Метод математической индукции. Перестановки. Размещения. Сочетания. Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Доказательства неравенств. Неравенство о среднем арифметическом и среднем геометрическом двух чисел. Делимость целых чисел. Деление с остатком. Сравнения по модулю m. Задачи с целочисленными неизвестными.
|
Уметь выполнять арифметические действия с действительными числами, сочетая устные и письменные приемы вычисления. Уметь сравнивать рациональные и действительные числа. Уметь применять метод мат. индукции для доказательства утверждений. Уметь решать задачи на перестановки, размещения, сочетания методом перебора, а также с использованием формул . Уметь решать задачи с целочисленными неизвестными. Уметь применять свойства делимости чисел, признак делимости чисел при доказательстве теорем.
|
Уметь отличать существенные и несущественные признаки и свойства математических объектов. Делать умозаключения и выводы. Определение сущностных характеристик изучаемого объекта: самостоятельный выбор критериев для сравнения, сопоставления, оценки и классификации объектов. |
|
|
| Блок1. Алгебра |
|
|
|
|
|
| Глава I![]() ![]() 1.Действительные числа. |
12 |
|
|
|
-
| Понятие действительного числа | 1 | 02.09. |
|
|
-
| Работа с действительными числами | 1 | 03.09. |
|
|
-
| Множества чисел | 1 | 04.09. |
|
|
-
| Свойства действительных чисел | 1 | 05.09. |
|
|
-
| Метод математической индукции. | 1 | 06.09. |
|
|
-
| Перестановки | 1 | 07.09. |
|
|
-
| Размещения | 1 | 09.09. |
|
|
-
| Сочетания | 1 | 10.09. |
|
|
-
| Доказательство числовых неравенств. | 1 | 11.09. |
|
|
-
| Делимость целых чисел. | 1 | 12.09. |
|
|
-
| Сравнение по модулю m. | 1 | 13.09. |
|
|
| 12.. | Задачи с целочисленными неизвестными.
| 1 | 14.09. |
|
|
|
| 2.Рациональные уравнения и неравенства. | 18 |
|
|
|
|
|
|
| 13. | Рациональные выражения | 1 | 16.09. |
| Знать схему Горнера, теорему Безу и следствия из теоремы Безу, делимость двучленов на двучлены, симметрические многочлены, формулы сокращенного умножения для старших степеней, бином Ньютона, алгоритм решения систем уравнений, алгебраических уравнений и знать методы решения алгебраических уравнений. Свойства биномиальных коэффициентов. Треугольник Паскаля. Многочлены от нескольких переменных, симметрические многочлены. Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
| Преобразовывать рациональные выражения Решать рациональные уравнения, системы рациональных уравнений Применять метод интервалов решения неравенств Уметь применять схему Горнера, теорему Безу и следствия из теоремы Безу; делимость двучлена на двучлен при решении уравнений разложением на множители. Уметь применять формулы бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля. Многочлены от нескольких переменных, симметрические многочлены. Применять математические методы для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений |
Умение соотносить приложенные усилия с полученными результатами своей деятельности. |
|
| 14. | Формулы бинома Ньютона, суммы и разности степеней | 1 | 17.09. |
|
|
| 15. | Применение формулы бинома Ньютона, суммы и разности степеней. | 1 | 18.09. |
|
|
| 16. | Деление многочленов с остатком. Алгоритм Евклида. Схема Горнера. | 1 | 19.09. |
|
|
| 17. | Теорема Безу | 1 | 20.09. |
|
|
| 18. | Корень многочлена. | 1 | 21.09. |
|
|
| 19. | Рациональные уравнения | 1 | 23.09. |
|
|
| 20. | Решение рациональных уравнений. | 1 | 24.09. |
|
|
| 21. | Системы рациональных уравнений. | 1 | 25.09. |
|
|
| 22. | Решение систем рациональных уравнений. | 1 | 26.09. |
|
|
| 23. | Метод интервалов решения неравенств | 1 | 27.09. |
|
|
| 24. | Решение неравенств методом интервалов | 1 | 28.09. |
|
|
| 25. | Рациональные неравенства | 1 | 30.09. |
|
|
| 26. | Решение рациональных неравенств | 1 | 01.10. |
|
|
| 27. | Нестрогие неравенства | 1 | 02.10. |
|
|
| 28. | Решение нестрогих неравенств | 1 | 03.10. |
|
|
| 29. | Системы рациональных неравенств
| 1 | 04.10. |
|
|
| 30.
| Контрольная работа №1 по теме «Рациональные уравнения и неравенства»
| 1 | 05.10. |
| К.р.№ 1 |
|
| Блок 2. Геометрия. |
|
|
|
|
|
|
|
|
| Глава VIII Некоторые сведения из планиметрии. | 12 |
|
| Знать свойство биссектрисы; углов и отрезков, связанных с окружностью; формул площадей треугольников; теоремы Чевы и Менелая; задачу Эйлера; определение эллипса, гиперболы, параболы и их уравнений; вписанные и описанные многоугольники, свойства и признаки вписанных и описанных четырехугольников. Решение задач с помощью геометрических преобразований и геометрических мест точек | Уметь решать задачи на нахождение площадей треугольников, вычислять длины биссектрис, медиан и высот треугольников; уметь находить углы между касательной прямой и хордой, углы с вершинами внутри и вне окружности, уметь вычислять радиусов вписанной и описанной окружностей
| Использовать приобретенные знания и умения для решения практических задач, связанных с нахождением геометрических величин.
|
|
| 31. | Работа над ошибками. Угол между касательной и хордой | 1 | 07.10. |
|
|
| 32. | Две теоремы об отрезках, связанных с окружностью. | 1 | 08.10. |
|
|
| 33. | Углы с вершинами внутри и вне круга | 1 | 09.10. |
|
|
| 34. | Вписанный четырехугольник. Описанный четырехугольник. | 1 | 10.10. |
|
|
| 35. | Теорема о медиане. | 1 | 11.10. |
|
|
| 36. | Теорема о биссектрисе треугольника. | 1 | 12.10. |
|
|
| 37. | Формулы площади треугольника. Формула Герона. | 1 | 14.10. |
|
|
| 38. | Задача Эйлера. | 1 | 15.10. |
|
|
| 39. | Теорема Менелая. | 1 | 16.10. |
|
|
| 40. | Теорема Чевы. | 1 | 17.10. |
|
|
| 41. | Эллипс. Гипербола. | 1 | 18.10. |
|
|
| 42. | Парабола. | 1 | 19.10. |
|
|
|
| Введение (аксиомы стереометрии и их следствия) | 3 |
|
|
|
|
|
|
| 43. | Предмет стереометрии. | 1 | 21.10. |
| Основные понятия стереометрии (точка, прямая, плоскость, пространство). Понятие об аксиоматическом способе построения геометрии. | Решать задачи на применение аксиом стереометрии и их следствий | Поиск нужной информации по заданной теме в источниках различного типа. |
|
| 44. | Аксиомы стереометрии. | 1 | 22.10. |
|
|
| 45. | Некоторые следствия из аксиом.
| 1 | 23.10. |
|
|
|
| Глава 1. Параллельность прямых и плоскостей
| 16 |
|
|
|
|
|
|
| 46. | Параллельные прямые в пространстве. | 1 | 24.10. |
|
Пересекающиеся, параллельные прямые. Параллельность прямой и плоскости, признаки и свойства. Скрещивающиеся прямые. Угол между прямыми в пространстве. |
Решать задачи на параллельность прямой и плоскости. Решать задачи на взаимное расположение прямых в пространстве, угол между прямыми. |
Использование элементов причинно-следственного и структурно-функционального анализа. Определение характеристик изучаемого объекта. |
|
| 47. | Параллельность трех прямых. | 1 | 25.10. |
|
|
| 48. | Параллельность прямой и плоскости. | 1 | 26.10. |
|
|
| 49. | Решение задач. | 1 | 28.10. |
|
|
| 50. | Скрещивающиеся прямые. | 1 | 29.10. |
|
|
| 51. | Углы с сонаправленными сторонами. | 1 | 30.10. |
|
|
| 52. | Угол между прямыми. | 1 | 31.10. |
|
|
| 53. | Решение задач. Контрольная работа №2 по теме «Параллельность прямых. Параллельность прямой и плоскости.» | 1 | 01.11. |
| К.р. № 2 |
| 54. | Работа над ошибками Параллельные плоскости.
| 1 | 02.11. |
|
Параллельность плоскостей, перпендикулярность плоскостей, признаки и свойства. Определение параллельных плоскостей; Расстояние между параллельными плоскостями.понятие тетраэдра и параллелепипеда; вершины, ребра грани параллелепипеда и тетраэдра, свойства параллелепипеда и диагонали параллелепипеда.
|
Изображать пространственные фигуры. Строить сечения. Решать задачи на построение сечений Уметь применять изученные понятия, признак параллельности прямой и плоскости, признак параллельности двух плоскостей при решении задач, уметь доказать теоремы от противного. | Умение импровизировать, реализовывать оригинальные замыслы с использованием разнообразных средств. Исследование несложных реальных связей и зависимостей. Самостоятельное создание алгоритмов познавательной деятельности для решения задач . |
|
|
|
|
|
|
|
|
| 55. | Свойства параллельных плоскостей. | 1 | 12.11. |
|
|
| 56. | Тетраэдр. | 1 | 13.11. |
|
|
| 57. | Параллелепипед. Свойства граней и диагоналей параллелепипеда. | 1 | 14.11. |
|
|
| 58. | Задачи на построение сечений. | 1 | 15.11. |
|
|
| 59. | Обобщающий урок по теме «Параллельность плоскостей. Тетраэдр и параллелепипед» | 1 | 16.11. |
|
|
| 60. | Контрольная работа №3 по теме «Параллельность плоскостей. Тетраэдр и параллелепипед». | 1 | 18.11. |
| К.р. № 3 |
| 61. | Работа над ошибками Зачет №1 по теме «Параллельность прямых и плоскостей» | 1 | 19.11. |
| Зачет № 1 |
|
| Блок 3. Алгебра. ![]() ![]() |
|
|
|
|
|
|
|
|
| Глава I. 3. Корень степени n | 12 |
|
|
|
|
|
|
| 62. | Функция и её график | 1 | 20.11. |
|
Понятие функции и ее графика. Функция у = хп Понятие корня степени п. Корни четной и нечетной степеней. Арифметический корень. Свойства корней степени п. Функция у= . Корень степени n1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Корень степени n из натурального числа. . Корень степени n1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Корень степени n из натурального числа.
|
Уметь применять понятие функции и ее графика. Функция у = хп Понятие корня степени п. Корни четной и нечетной степеней. Арифметический корень. Свойства корней степени п. Функция у= . Корень степени n1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Корень степени n из натурального числа. . Корень степени n1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Корень степени n из натурального числа.
|
Поиск нужной информации по заданной теме в источниках различного типа. Понимание ценности образования как средства развития культуры личности. |
|
| 63. | Функция у = хn | 1 | 21.11. |
|
|
| 64. | Функция у = хnи его свойства | 1 | 22.11. |
|
|
| 65. | Понятие корня степени n | 1 | 23.11. |
|
|
| 66. | Корни четной и нечетной степеней. | 1 | 25.11. |
|
|
| 67. | Вычисление арифметических корней. | 1 | 26.11. |
|
|
| 68. | Свойства корней степени n | 1 | 27.11. |
|
|
| 69. | Применение свойств корней степени n. | 1 | 28.11. |
|
|
| 70. | Функция у= ![]() ![]() ![]() (х (х![]() ![]() 0). 0).
| 1 | 29.11. |
|
|
| 71. | Функция у= ![]() ![]() ![]() . .
| 1 | 30.11 |
|
|
| 72. | Корень степени n из натурального числа. | 1 | 02.12. |
|
|
| 73. | Контрольная работа №4 по теме «Корень степени n»
| 1 | 03.12. |
| К.р. № 4 |
|
| Блок 4 .Алгебра. |
|
|
|
|
|
|
|
|
| Глава I 4. Степень положительного числа. | 13 |
|
|
|
|
|
|
| 74. | Работа над ошибками. Степень с рациональным показателем. | 1 | 04.12. |
| Понятие и свойства степени с рациональным показателем. Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма. Теоремы о пределах последовательностей. Переход к пределам в неравенствах. Свойства пределов. Бесконечно убывающая геометрическая прогрессия. Число е. Понятие степени с иррациональным показателем. Показательная функция (экспонента), ее свойства и график.
|
Уметь переводить бесконечную периодическую дробь в обыкновенную; находить значение корней п-ой степени; выполнять тождественные преобразования выражений, использовать свойства степени к преобразованию иррациональных выражений.. |
Производить построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин и реальной жизни. |
|
| 75. | Свойства степени с рациональным показателем. | 1 | 05.12. |
|
|
| 76. | Применение свойства степени с рациональным показателем.
| 1 | 06.12. |
|
|
| 77. | Понятие предела последовательности. | 1 | 07.12. |
|
|
| 78. | Вычисление пределов последовательности . | 1 | 09.12. |
|
|
| 79. | Свойства пределов. | 1 | 10.12. |
|
|
| 80. | Применение свойства пределов. | 1 | 11.12. |
|
|
| 81. | Бесконечно убывающая геометрическая прогрессия. | 1 | 12.12. |
|
|
| 82. | Число е | 1 | 13.12. |
|
|
| 83. | Понятие степени с иррациональным показателем. | 1 | 14.12. |
|
|
| 84. | Показательная функция | 1 | 16.12. |
|
|
| 85. | Построение графиков показательных функций. | 1 | 17.12. |
|
|
| 86. | Контрольная работа №5 по теме «Степень положительного числа» | 1 | 18.12. |
| К.р. № 5 |
|
| Блок 5. Алгебра. |
|
|
|
|
|
|
|
|
| Глава I. 5. Логарифмы. | 6 |
|
|
|
|
|
|
| 87. | Работа над ошибками. Понятие логарифма | 1 | 19.12. |
|
Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е. Логарифмическая функция, ее свойства и график Преобразования выражений, включающих арифметические операции, а также операции возведения в степень и логарифмирования.
|
Выработать умение преобразовывать выражения, содержащие логарифмы. |
Производить планирования и осуществления алгоритмической деятельности. |
|
| 88. | Свойства логарифмов | 1 | 20.12. |
|
|
| 89. | Применение свойств логарифмов | 1 | 21.12. |
|
|
| 90. | Логарифмическая функция
| 1 | 23.12. |
|
|
| 91. | Десятичные логарифмы. | 1 | 24.12 |
|
|
| 92. | Степенные функции.
| 1 | 25.12. |
|
|
|
| 6. Показательные и логарифмические уравнения и неравенства. | 11 |
|
|
|
|
|
|
| 93. | Простейшие показательные уравнения | 1 | 26.12. |
|
Решение простейших показательных и логарифмических уравнений и неравенств. Уравнения, сводящиеся к простейшим заменой неизвестного.. Неравенства, сводящиеся к простейшим заменой неизвестного.
| Уметь применять свойства показательной функции при решении типовых показательных уравнений и неравенств, систем уравнений с двумя переменными и неравенств с одной переменной. Уметь находить логарифм числа, уметь применять свойства логарифмов при выполнении тождественных преобразованиях выражений, содержащих логарифмы; решать логарифмические уравнения, неравенства и систем уравнений различными способами.
| Уметь абстрагировать, отличать существенные и несущественные свойства математических объектов. Делать умозаключения и выводы Уметь выделять признаки и свойства одного и того же объекта. Проведение доказательных рассуждений, логического обоснования выводов, использования различных языков математики для иллюстрации, аргументации и доказательства.
|
|
| 94. | Простейшие логарифмические уравнения | 1 | 27.12. |
|
|
| 95. | Уравнения, сводящиеся к простейшим заменой неизвестного.
| 1 | 28.12. |
|
|
|
| II полугодие | 115 |
|
|
|
| 96. | Решение уравнений, сводящихся к простейшим заменой неизвестного.
| 1 | 12.01. |
|
|
| 97. | Простейшие показательные неравенства. | 1 | 13.01. |
|
|
| 98. | Решение простейших показательных неравенств. | 1 | 14.01. |
|
|
| 99 | Простейшие логарифмические неравенства | 1 | 15.01. |
|
|
| 100. | Решение логарифмических неравенств. | 1 | 16.01 |
|
|
| 101. | Неравенства, сводящиеся к простейшим заменой неизвестного. | 1 | 17.01. |
|
|
| 102. | Решение неравенств, сводящихся к простейшим заменой неизвестного. | 1 | 19.01. |
|
|
| 103. | Контрольная работа №6 по теме «Показательные и логарифмические уравнения и неравенства»
| 1 | 20.01. |
| К.р. № 6 |
|
| Блок 6. Геометрия. |
|
|
|
|
|
|
|
|
| Глава 2. Перпендикулярность прямых и плоскостей. | 17 |
|
|
|
|
|
|
| 104. | Работа над ошибками. Перпендикулярные прямые в пространстве. | 1 | 21.01. |
| Знать перпендикулярность прямых; перпендикулярность прямой и плоскости, признаки и свойства. Теорема о трех перпендикулярах. Перпендикуляр и наклонная к плоскости. Угол между прямой и плоскостью. Параллельность плоскостей, перпендикулярность плоскостей, признаки и свойства. Двугранный угол, линейный угол двугранного угла. Расстояния от точки до плоскости. Расстояние отпрямой до плоскости. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми. Параллельное проектирование. Ортогональное проектирование. Площадь ортогональной проекции многоугольника. Изображение пространственных фигур. Центральное проектирование. |
Уметь пользоваться изученными понятиями, свойствами, признаками при решении задач на нахождение углов между прямыми, между прямой и плоскостью, между плоскостями. Уметь находить расстояния междупрямыми, между прямой и плоскостью, между плоскостями, находить площади ортогональной проекции многоугольника.
|
Уметь пользоваться математическими понятиями, символикой, суждениями, использовать алгоритм решения задач, выбор рациональных методов решения
|
|
| 105. | Параллельные прямые, перпендикулярные к плоскости. | 1 | 22.01. |
|
|
| 106. | Признак перпендикулярности прямой и плоскости. | 1 | 23.01. |
|
|
| 107. | Теорема о прямой, перпендикулярной к плоскости. | 1 | 24.01. |
|
|
| 108. | Решение задач на перпендикулярность прямой и плоскости. | 1 | 26.01. |
|
|
| 109. | Расстояние от точки до плоскости. | 1 | 27.01. |
|
|
| 110. | Теорема о трех перпендикулярах. | 1 | 28.01. |
|
|
| 111. | Решение задач на применение теоремы о трех перпендикулярах. | 1 | 29.01. |
|
|
| 112. | Угол между прямой и плоскостью. | 1 | 30.01. |
|
|
| 113. | Решение задач по теме «Угол между прямой и плоскостью». | 1 | 31.02. |
|
|
| 114. | Обобщение темы «Угол между прямой и плоскостью». | 1 | 02.02. |
|
|
| 115. | Двугранный угол. Свойство двугранного угла. | 1 | 03.02. |
|
|
| 116. | Признак перпендикулярности двух плоскостей.
| 1 | 04.02. |
|
|
| 117. | Прямоугольный параллелепипед. | 1 | 05.02. |
|
|
| 118. | Трехгранный угол. Многогранный угол. | 1 | 06.02. |
|
|
| 119. | Контрольная работа №7 по теме «Перпендикулярность прямых и плоскостей». | 1 | 07.02. |
| К.р. № 7 |
| 120. | Работа над ошибками. Зачет №2 по теме «Перпендикулярность прямых и плоскостей»
| 1 | 09.02. |
| Зачет №2 |
|
| Блок 7. Алгебра. |
|
|
|
|
|
|
|
|
| Глава II 7. Синус и косинус угла. | 7 |
|
|
|
|
|
|
| 121. | Понятие угла | 1 | 11.02. |
|
Синус, косинус произвольного угла. Радианная мера угла. Синус, косинус числа. Основные тригонометрические тождества. Арксинус, арккосинус числа. | Уметь определять положение точки на тригонометрическом круге, переводить углы из радианной меры в градусную и из градусной в радианную, применять изученные формулы к преобразованию тригонометрических выражений
|
Умение решать широкий класс задач из различных разделов курса, поисковой и творческой деятельности . |
|
| 122. | Радианная мера угла | 1 | 12.02. |
|
|
| 123. | Определение синуса и косинуса угла | 1 | 13.02. |
|
|
| 124. | Основные формулы для sin α и cos α. | 1 | 14.02. |
|
|
| 125. | Применение основных формул для sin α и cos α. | 1 | 15.02. |
|
|
| 126. | Арксинус. Арккосинус. Примеры использования арксинуса и арккосинуса. | 1 | 17.02. |
|
|
| 127. | Формулы для арксинуса и арккосинуса. | 1 | 18.02. |
|
|
|
| 8.Тангенс и котангенс угла. | 6 |
|
|
|
|
|
|
| 128. | Определение тангенса и котангенса угла. | 1 | 19.02. |
|
|
|
|
|
| 129. | Основные формулы для tg α и ctg α. | 1 | 20.02. |
| Тангенс, котангенс произвольного угла. Радианная мера угла. Тангенс и котангенс числа. Основные тригонометрические тождества. Арктангенс, арккотангенс числа | Применять свойства функций угла: tg a и ctg a. С использованием единичной окружности вводить понятия линий тангенса и котангенса;применять изученные формулы к преобразованию тригонометрических выражений
| Умение решать широкий класс задач из различных разделов курса, поисковой и творческой деятельности при решении задач |
|
| 130. | Применение основных формул для tg α и ctg α. | 1 | 21.02. |
|
|
| 131. | Арктангенс. Арккотангенс. Примеры использования арктангенса и арккотангенса. | 1 | 22.02. |
|
|
| 132. | Формулы для арктангенса и арккотангенса. | 1 | 24.02. |
|
|
| 133. | Контрольная работа №8 по теме «Синус и косинус угла. Тангенс и котангенс угла» | 1 | 25.02. |
| К.р. №8 |
|
| 9. Формулы сложения. | 11 |
|
|
|
|
|
|
| 134. | Работа над ошибками. Косинус разности и косинус суммы двух углов. | 1 | 26.02. |
|
Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента.
Преобразования тригонометрических выражений
|
Умение выполнять тождественные преобразования тригонометриче-ских выражений с использованием выведенных формул; применять изученные формулы к преобразованию тригонометрических выражений
|
Умение проводить доказательные рассуждения, логические обоснования выводов, использования различных языков математики для иллюстрации, интерпретации, аргументации и доказательства.
|
|
| 135. | Применение формул косинуса разности и косинуса суммы двух углов. | 1 | 27.02. |
|
|
| 136. | Формулы для дополнительных углов. | 1 | 28.02. |
|
|
| 137. | Синус суммы и синус разности двух углов. | 1 | 01.03. |
|
|
| 138. | Применение синуса суммы и синуса разности двух углов. | 1 | 03.03. |
|
|
| 139. | Сумма и разность синусов и косинусов.
| 1 | 04.03. |
|
|
| 140 | Применение суммы и разности синусов и косинусов . | 1 | 05.03. |
|
|
| 141. | Формулы для двойных и половинных углов. | 1 | 06.03. |
|
|
| 142. | Применение формулы для двойных и половинных углов. | 1 | 07.03. |
|
|
| 143. | Произведение синусов и косинусов.
| 1 | 08.03. |
|
|
| 144. | Формулы для тангенсов. | 1 | 10.03. |
|
|
|
| 10. Тригонометрические функции числового аргумента | 9 |
|
|
|
|
|
|
| 145. | Функция у = sin х. | 1 | 11.03. |
|
Функции у = sinх,у =cos х, у = tg х, у= ctg х Тригонометрические функции, их свойства и графики, периодичность, основной период. Обратные тригонометрические функции, их свойства и графики. |
Рассматривать функции как функции числа, используя свойства тригонометрических функций строить их графики |
Уметь определять значение функции по значению аргумента при различных способах задания функции |
|
| 146. | Применение свойств функции у = sin х. | 1 | 12.03. |
|
|
| 147. | Функция у = cos х. | 1 | 13.03. |
|
|
| 148. | Применение свойств функции у = cos х. | 1 | 14.03. |
|
|
| 149. | Функция у = tg х. | 1 | 15.03. |
|
|
| 150 | Применение свойств функции у = tg х. | 1 | 17.03. |
|
|
| 151. | Функция у = ctg х. | 1 | 18.03. |
|
|
| 152. | Применение свойств функции у = ctg х. | 1 | 19.03. |
|
|
| 153. | Контрольная работа №9 по теме «Формулы сложения. Тригонометрические функции числового аргумента»
| 1 | 20.03. |
| К.р. № 9 |
|
| Блок 8. Геометрия |
|
|
|
|
|
|
|
|
| Глава 3. Многогранники
| 14 |
|
|
|
|
|
|
| 154. | Работа над ошибками. Понятие многогранника. | 1 | 21.03. |
| Понятие Вершины, ребра, грани многогранника. Развертка. Многогранные углы. Выпуклые многогранники. Теорема Эйлера. Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Сечения многогранников. Построение сечений. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр). |
Доказывать теорему о площади боковой поверхности прямой призмы, теорему о площади боковой поверхности правильной пирамиды. Решать задачи на многогранники, симметрию в пространстве. Уметь изображать параллелепипед, призму, пирамиду, усеченную пирамиду и развертки правильных многогранников. Уметь решать задачи на нахождение площадей поверхности призмы и пирамиды.
|
Извлечение необходимой информации из источников, созданных в различных знаковых системах, отделение основной информации от второстепенной, критическое оценивание достоверности полученной информации |
|
| 155. | Теорема Эйлера. Призма. | 1 | 22.03. |
|
|
|
|
|
|
|
|
|
| 156. | Пространственная теорема Пифагора. | 1 | 01.04. |
|
|
| 157. | Пирамида. | 1 | 02.04. |
|
|
| 158. | Правильная пирамида. | 1 | 03.04. |
|
|
| 159. | Усеченная пирамида. Площадь поверхности пирамиды. | 1 | 04.04. |
|
|
| 160. | Решение задач по теме «Пирамида» | 1 | 05.04. |
|
|
| 161. | Симметрия в пространстве. | 1 | 07.04. |
|
|
| 162. | Понятие правильного многогранника. | 1 | 08.04. |
|
|
| 163. | Элементы симметрии правильных многогранников. | 1 | 09.04. |
|
|
| 164. | Решение задач на правильные многогранники | 1 | 10.04. |
|
|
| 165. | Обобщающий урок по теме «Многогранники» | 1 | 11.04. |
|
|
| 166. | Контрольная работа №10 по теме «Многогранники» | 1 | 12.04. |
| К.р. № 10 |
| 167 | Работа над ошибками. Зачет №3 | 1 | 14.04. |
| Зачет № 3 |
|
| Блок 9. Алгебра.
|
|
|
|
|
|
|
|
|
| Глава II 11. Тригонометрические уравнения и неравенства. | 12 |
|
|
|
|
|
|
| 168. | Простейшие тригонометрические уравнения. | 1 | 15.04. |
|
Простейшие тригонометрические уравнения. Тригонометрические уравнения, сводящиеся к простейшим заменой неизвестного. Применение основных тригонометрических формул для решения уравнений. Однородные уравнения. Решение простейших тригонометрических уравнений.
|
Уметь находить арксинус, арккосинус, арктангенс и арккотангенс чисел; уметь решать простейшие тригонометри- ческие уравнения и систем уравнений, неравенства, используя методы их решения; решать однородные уравнения.
|
Уметь решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления.
|
|
| 169. | Решение простейших тригонометрических уравнений. | 1 | 16.04. |
|
|
| 170. | Уравнения, сводящиеся к простейшим заменой неизвестного. | 1 | 17.04. |
|
|
| 171. | Решение уравнений, сводящихся к простейшим заменой неизвестного. | 1 | 18.04. |
|
|
| 172. | Применение основных тригонометрических формул для решения уравнений.
| 1 | 19.04. |
|
|
| 173. | Решение тригонометрических уравнений. | 1 | 21.04. |
|
|
| 174. | Однородные уравнения. | 1 | 22.04. |
|
|
| 175. | Простейшие неравенства для синуса и косинуса. | 1 | 23.04. |
|
|
| 176. | Простейшие неравенства для тангенса и котангенса. | 1 | 24.04. |
|
|
| 177. | Неравенства, сводящиеся к простейшим заменой неизвестного. | 1 | 25.04. |
|
|
| 178. | Введение вспомогательного угла Замена неизвестного t=sinx + cosx. | 1 | 26.04. |
|
|
| 179. | Контрольная работа №11 по теме «Тригонометрические уравнения и неравенства» | 1 | 28.04. |
| К.р. №11 |
|
| Глава III Элементы теории вероятности . |
|
|
|
|
|
|
|
|
| 12. Вероятность события | 6 |
|
|
|
|
|
|
| 180. | Работа над ошибками. Понятие вероятности события. | 1 | 29.04. |
|
Знать понятие и свойства вероятности события.
|
Уметь применять события вероятности Свойства вероятностей событий
|
Определение сущностных характеристик изучаемого объекта: самостоятельный выбор критериев для сравнения, |
|
| 181. | Применение понятия вероятности события. | 1 | 30.04. |
|
|
| 182. | Решение задач. | 1 | 01.05. |
|
|
| 183. | Свойства вероятности события. | 1 | 02.05. |
|
|
| 184. | Применение свойств вероятности события. | 1 | 03.05. |
|
|
| 185. | Решение задач. | 1 | 05.05. |
|
|
|
| 13. Частота. Условная вероятность. | 2 |
|
|
|
| 186. | Относительная частота события.* | 1 | 06.05. |
| Относительная частота событий Условная вероятность. Независимость событий | сопоставления, оценки и классификации объектов. |
|
| 187. | Условная вероятность. Независимые события.*
| 1 | 07.05. |
|
|
|
| Блок 10. Повторение курса алгебры и геометрии. | 23 |
|
|
|
|
|
|
| 188. | Действительные числа. | 1 | 08.05. |
|
Знать формулы площади поверхности призмы, пирамиды и усеченной пирамиды. Знать тригонометри- ческие формулы, способы решения логарифмических и показательных уравнений, уравнений с целыми коэффициентами; знать способы решения показательных, логарифмических и тригонометрических неравенств
|
Уметь применять теоретический материал при решении задач на нахождение площади поверхности призмы и пирамиды, усеченной пирамиды Уметь решать показательные, тригонометрические уравнения и неравенства.
|
Уметь работать с тестами, составлять математические модели практических задач.
Уметь выбирать оптимальный способ решения, давать своей работе адекватную самооценку. |
|
| 189. | Рациональные уравнения и неравенства
| 1 | 09.05. |
|
|
| 190. | Корень степени n. | 1 | 10.05. |
|
|
| 191. | Степень положительного числа. | 1 | 12.05. |
|
|
| 192. | Логарифмы. | 1 | 13.05. |
|
|
| 193. | Показательные уравнения . | 1 | 14.05. |
|
|
| 194. | Показательные неравенства. | 1 | 15.05. |
|
|
| 195. | Логарифмические уравнения. | 1 | 16.05. |
|
|
| 196. | Логарифмические неравенства
| 1 | 17.05. |
|
|
| 197. | Тригонометрические функции числового аргумента. | 1 | 19.05. |
|
|
| 198. | Итоговая контрольная работа №12 за курс 10 класса. | 1 | 20.05. |
| К.р. № 12 |
| 199. | Анализ контрольной работы. Работа над ошибками. | 1 | 21.05. |
|
|
| 200. | Тригонометрические уравнения. | 1 | 22.05. |
|
|
| 201. | Тригонометрические неравенства | 1 | 23.05. |
|
|
| 202. | Некоторые сведения из планиметрии. | 1 | 24.05. |
|
|
| 203. | Аксиомы стереометрии. | 1 | 26.05. |
|
|
| 204. | Параллельность прямых и плоскостей. | 1 | 27.05. |
|
|
| 205. | Перпендикулярность прямых и плоскостей | 1 | 28.05. |
|
|
| 206. | Многогранники | 1 | 29.05. |
|
|
| 207. | Повторение. Решение задач. | 1 | 30.05. |
|
|
| 208. | Комбинаторика Элементы теории вероятностей
| 1 | 31.05. |
|
|
| 209. | Решение тестов из ЕГЭ
| 1 | резерв |
|
|
| 210 | Заключительный урок. | 1 | резерв |
|
|
6. Критерии и нормы оценки
Оценка знаний–систематический процесс, который состоит в определении степени соответствия имеющихся знаний, умений, навыков, предварительно планируемым. Первое необходимое условие оценки: планирование образовательных целей; без этого нельзя судить о достигнутых результатах. Второе необходимое условие-установление фактического уровня знаний и сопоставление его заданным.
Процесс оценки включает в себя такие компоненты: определение целей обучения; выбор контрольных заданий, проверяющих достижение этих целей; отметку или другой способ выражения результатов проверки. Все компоненты оценки взаимосвязаны. И каждый влияет на все последующие.
В зависимости от поставленных целей по-разному строится программа контроля, подбираются различные типы вопросов и заданий. Но применение примерных норм оценки знаний должно внести единообразие в оценку знаний и умений учащихся и сделать ее более объективной. Примерные нормы представляют основу, исходя из которой, учитель оценивает знания и умения учащихся.
1. Содержание и объем материала, подлежащего проверке и оценке, определяются программой по математике для средней школы. В задания для проверки включаются основные, типичные и притом различной сложности вопросы, соответствующие проверяемому разделу программы.
При проверке знаний и умений, учащихся учитель выявляет не только степень усвоения учащимися теории и умения применять ее на практике, но также умение самостоятельно мыслить.
2. Основными формами проверки знаний и умений учащихся по математике в средней школе являются устный опрос и письменная контрольная работа, наряду с которыми применяются и другие формы проверки. При этом учитывается, что в некоторых случаях только устный опрос может дать более полные представления о знаниях и умениях учащихся; в тоже время письменная контрольная работа позволяет оценить умение учащихся излагать свои мысли на бумаге; навыки грамотного и фактически грамотного оформления выполняемых ими заданий.
3. При оценке устных ответов и письменных контрольных работ учитель в первую очередь учитывает имеющиеся у учащегося фактические знания и умения, их полноту, прочность, умение применять на практике в различных ситуациях. Результат оценки зависит также от наличия и характера погрешностей, допущенных при устном ответе или письменной контрольной работе.
4. Среди погрешностей выделяются ошибки, недочеты и мелкие погрешности.
Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями и их применением.
К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в соответствии с программой основными. К недочетам относятся погрешности, объясняющиеся рассеянностью или недосмотром, но которые не привели к искажению смысла полученного учеником задания или способа его выполнения. Грамматическая ошибка, допущенная в написании известного учащемуся математического термина, небрежная запись, небрежное выполнение чертежа считаются недочетом.
К мелким погрешностям относятся погрешности в устной и письменной речи, не искажающие смысла ответа или решения, случайные описки и т. п.
5. К ошибкам, например, относятся:
-неправильный выбор порядка выполнения действий в выражении;
-пропуск нуля в частном при делении натуральных чисел или десятичных дробей;
-неправильный выбор знака в результате выполнения действий над положительными и отрицательными числами; а так же при раскрытии скобок и при переносе слагаемых из одной части уравнения в другую;
- неправильный выбор действий при решении текстовых задач;
-неправильное измерение или построение угла с помощью транспортира, связанное с отсутствием умения выбирать нужную шкалу;
-неправильное проведение перпендикуляра к прямой или высот в тупоугольном треугольнике;
-умножение показателей при умножении степеней с одинаковыми основаниями;
-“сокращение” дроби на слагаемое;
-замена частного десятичных дробей частным целых чисел в том случае, когда в делителе после запятой меньше цифр, чем в делимом;
-сохранение знака неравенства при делении обеих его частей на одно и тоже отрицательное число;
-неверное нахождение значения функции по значению аргумента и ее графику;
-потеря корней при решении тригонометрических уравнений, а так же уравнений вида  и
и  ;
;
-непонимание смысла решения системы двух уравнений с двумя переменными как пары чисел;
-незнание определенных программой формул (формулы корней квадратного уравнения, формул производной частного и произведения, формул приведения, основных тригонометрических тождеств и др.);
-приобретение посторонних корней при решении иррациональных, показательных и логарифмических уравнений;
-погрешность в нахождении координат вектора;
-погрешность в разложении вектора по трем неколлинеарным векторам, отложенным от разных точек;
-неумение сформулировать предложение, обратное данной теореме;
-ссылка при доказательстве или обосновании решения на обратное утверждение, вместо прямого;
- использование вместо коэффициента подобия обратного ему числа.
6. Примеры недочетов:
-неправильная ссылка на сочетательный и распределительный законы при вычислениях;
-неправильное использование в отдельных случаях наименований, например, обозначение единиц длины для единиц площади и объема;
-сохранение в окончательном результате при вычислениях или преобразованиях выражений неправильной дроби или сократимой дроби;
-приведение алгебраических дробей не к наиболее простому общему знаменателю;
-случайные погрешности в вычислениях при решении геометрических задач и выполнении тождественных преобразований.
7. Граница между ошибками и недочетами является в некоторой степени условной. В одно время при одних обстоятельствах допущенная учащимися погрешность может рассматриваться как ошибка, в другое время и при других обстоятельствах она может рассматриваться как недочет.
8. Каждое задание для устного опроса или письменной контрольной работы представляет теоретический вопрос или задачу.
Ответ на вопрос считается безупречным, если его содержание точно соответствует вопросу, включает все необходимые теоретические сведения, обоснованные заключения и поясняющие примеры, а его изложение и оформление отличаются краткостью и аккуратностью.
Решение задачи считается безупречным, если получен верный ответ при правильном ходе решения, выбран соответствующий задаче способ решения, правильно выполнены необходимые вычисления и преобразования, последовательно и аккуратно оформлено решение.
9. Оценка ответа учащегося при устном опросе и оценка письменной контрольной работы проводится по пятибалльной системе.
Как за устный ответ, так и за письменную контрольную работу может быть выставлена одна из отметок:5,4,3,2,1.
10. Оценка устных ответов.
а)Ответ оценивается отметкой “5”, если учащийся:
1) полностью раскрыл содержание материала в объеме, предусмотренном программой и учебником;
2) изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
3) правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
4) показал умение иллюстрировать теорию конкретными примерами, применять в новой ситуации при выполнении практического задания;
5) продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;
6) отвечая самостоятельно, без наводящих вопросов учителя.
Возможны 1-2 неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
б) Ответ оценивается отметкой “4”, если удовлетворяет в основном требованиям на оценку “5”, но при этом имеет один из недочетов:
1) в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;
2) допущены 1-2 недочета при освещении основного содержания ответа, исправленные после замечания учителя;
3) допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
в) Ответ оценивается отметкой “3”, если:
1) неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программы;
2) имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
3) ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил обязательное задание.
г) Ответ оценивается отметкой “2”, если:
1) не раскрыто содержание учебного материала;
2) обнаружено незнание или не понимание учеником большей или наиболее важной части учебного материала;
3) допущены ошибки в определении понятия, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
11. Оценивание письменных контрольных работ.
При проверке письменных работ по математике следует различать грубые и негрубые ошибки.
К грубым ошибкам относятся:
-вычислительные ошибки в примерах и задачах;
-ошибки на незнание порядка выполнения арифметических действий;
-неправильное решение задачи (пропуск действий, неправильный выбор действий, лишнее действие);
-недоведение до конца решения задачи или примера;
-невыполненное задание.
К негрубым ошибкам относятся:
-нерациональные приемы вычислений;
- неправильная постановка вопроса к действию при решении задачи;
-неверно сформулированный ответ задачи;
-неправильное списывание данных чисел, знаков;
-недоведение до конца преобразований.
При оценке работ, включающих в себя проверку вычислительных навыков, ставятся следующие отметки:
“5”- работа выполнена безошибочно;
“4”- в работе допущены 1 грубая и 1-2 негрубые ошибки;
“3”- в работе допущены 2-3 грубые или 3 и более негрубые ошибки;
“2”- если в работе допущены 4 и более грубых ошибок.
При оценке работ, состоящих только из задач, ставятся следующие отметки:
“5”- если задачи решены без ошибок;
“4”- если допущены 1-2 негрубые ошибки;
“3”- если допущены 1 грубая и 3-4 негрубые ошибки;
“2”- если допущено 2 и более грубых ошибок.
12. Учитель может повысить отметку за оригинальный ответ или оригинальное решение, которые свидетельствуют о высоком математическом развитии учащегося, а так же за решение более сложной задачи или ответа на наиболее трудный вопрос, предложенные сверх обычных заданий.
Оценивая ответ учащегося или письменную контрольную работу, учитель дает устно качественную характеристику их выполнения.
13. Оценивание решения одной задачи, одного примера, ответа на один вопрос.
Это необходимо, т. к. при устном опросе почти всегда дается один вопрос, у доски, да часто и самостоятельно в классе учащиеся решают одну задачу. К тому же умение оценивать решение одной задачи облегчает оценку комплексного задания.
Решение задачи обычно состоит из нескольких этапов:
а) осмысление условия и цели задачи;
б) возникновение плана решения;
в) осуществление намеченного плана;
г) проверка полученного результата.
Оценивая выполненную работу, естественно учитывать результаты деятельности учащегося на каждом этапе; правильность высказанной идеи, плана решения, а так же степень осуществления этого плана при выставлении оценки нужно считать решающими. Т.о., при оценке решения задачи необходимо учитывать, насколько правильно учащийся понял ее, высказал ли он плодотворную идею и как осуществил намеченный план решения, какие навыки и умения показал, какие использовал знания.
При устном ответе по теоретическому материалу решающим является умение рассуждать, аргументировать, применять ранее изученный материал в доказательствах, видеть связи между понятиями, а так же уметь грамотно и стройно излагать свои мысли.
Приведем пример.
Ученик решает задачу, где важнейшим является составление системы уравнений. Если он получил систему, но не довел решение до конца, то можно выставить “4”. Если же основная трудность состоит в решении полученной системы, то за ее составление можно выставить “3”.
Критерии ошибок:
К г р у б ы м ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять; незнание приемов решения задач, рассматриваемых в учебниках, а также вычислительные ошибки, если они не являются опиской;
К н е г р у б ы м ошибкам относятся: потеря корня или сохранение в ответе постороннего корня; отбрасывание без объяснений одного из них и равнозначные им;
К н е д о ч е т а м относятся: нерациональное решение, описки, недостаточность или отсутствие пояснений, обоснований в решениях
Оценка устных ответов учащихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотрен ном программой и учебником,
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую термино логию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при от работке умений и навыков;
отвечал самостоятельно без наводящих вопросов учителя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по за мечанию учителя.
Ответ оценивается отметкой «4», если он удовлетворяет воснов ном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившие ма тематическое содержание ответа;
допущены один – два недочета при освещении основного содержа ния ответа, исправленные по замечанию учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.
Отметка «3» ставится в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»);
имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, вы кладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Оценка письменных контрольных работ учащихся
по математике
Отметка «5» ставится, если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробе лов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что учащийся не владеет
обязательными умениями по данной теме в полной мере
Оценка выполнения тестовых заданий
Таблица пересчета для выставления отметок за тестирование
| Число заданий в тесте | Отметка |
| «2» | «3» | «4» | «5» |
| 9 | 5 и менее | 6 | 7-8 | 9 |
| 12 | 7 и менее | 8 | 9-10 | 11-12 |
| 15-16 | 9 и менее | 10 | 11-13 | 14-16 |
| 18 | 11 и менее | 12-13 | 14-16 | 17-18 |
| 24 | 15 и менее | 16-18 | 19-21 | 22-24 |
| 30 | 19 и менее | 20-23 | 24-27 | 28-30 |
- выполнение заданий на 95% - 100 % - «5»
-выполнение заданий на 85% - 94% - «4»
- выполнение заданий на 75% - 84% -«3»
- выполнение заданий менее 75% -«2»
График контрольных работ
|
№ п/п
|
Контрольные работы |
Дата проведения |
| План | Факт |
| 1 | Контрольная работа №1 по теме «Рациональные уравнения и неравенства» | 05.10. |
|
| 2 | Контрольная работа №2 по теме «Параллельность прямых. Параллельность прямой и плоскости.» | 01.11. |
|
| 3 | Контрольная работа №3 по теме «Параллельность плоскостей. Тетраэдр и параллелепипед». | 18.11. |
|
| 4 | Контрольная работа №4 по теме «Корень степени n»
| 03.12. |
|
| 5 | Контрольная работа №5 по теме «Степень положительного числа» | 18.12. |
|
| 6 | Контрольная работа №6 по теме «Показательные и логарифмические уравнения и неравенства»
| 21.01. |
|
| 7 | Контрольная работа №7 по теме «Перпендикулярность прямых и плоскостей». | 08.02. |
|
| 8 | Контрольная работа №8 по теме «Синус и косинус угла. Тангенс и котангенс угла» | 25.02. |
|
| 9 | Контрольная работа №9 по теме «Формулы сложения. Тригонометрические функции числового аргумента»
| 20.03. |
|
| 10 | Контрольная работа №10 по теме «Многогранники» | 12.04. |
|
| 11 | Контрольная работа №11 по теме «Тригонометрические уравнения и неравенства» | 28.04. |
|
| 12 | Итоговая контрольная работа №12 за курс 10 класса. | 20.05. |
|
График зачетов и тестовых заданий
| № п/п | Зачеты и тестовые задания | Дата проведения |
| по плану | фактически |
| 1. | Зачет №1 по теме «Параллельность прямых и плоскостей» | 19.11 |
|
| 2 | Тест по теме «Свойства корней степени n». | 29.11 |
|
| 3. | Тест по теме «Степень с рациональным показателем». | 05.12. |
|
| 4. | Тест по теме «Решение показательных и логарифмических уравнений». | 14.01. |
|
| 5. | Зачет №2 по теме «Перпендикулярность прямых и плоскостей» | 10.02. |
|
| 6. | Тест по теме «Применение основных формул для синуса и косинуса». | 14.02. |
|
| 7. | Тест по теме «Основные формулы для тангенса и котангенса». | 21.02. |
|
| 8. | Тест по теме «Формулы сложения» | 04.03. |
|
| 9. | Тест по теме «Формулы сложения». | 12.03. |
|
| 10. | Тест по теме «Призма и пирамида». | 04.04. |
|
| 11. | Зачет №3 по теме «Многогранники». | 12.04 |
|
| 12. | Тест по теме «Решение тригонометрических уравнений». | 24.04. |
|
| 13. | Тест по теме «Решение тригонометрических неравенств». | . 05.05. |
|
8.Литература и средства обучения, в том числе и ЭОР
Учебно-методический комплекс по математике на 2014 -2015 учебный год.
| Кл. | Предмет | Кол. | Программа | Учебник | Методический материал |
| 10
| Математика | 210 | Программы общеобразовательных учреждений. Алгебра и начала математического анализа, 10-11 кл. Составитель: Т.А. Бурмистрова,- М.: Просвещение, 2009г., Программы общеобразовательных учреждений. Геометрия, 10-11 кл. Составитель: Т.А. Бурмистрова,- М.: Просвещение, 2009г., | Учебник «Алгебра и начала анализа 10 класс» авторы С.М.Никольский и др. - М.: Просвещение, 2010 г., рекомендовано Министерством образования и науки РФ Учебник «Геометрия, 10-11» авторы: Л.С. Атанасян, В.Ф. Бутузов и др., - М.: Просвещение, 2010 г. рекомендован министерством образования РФ. | Книга для учителя М.К. Потапов, А.В. Шевкин «Алгебра и начала анализа: 10 кл.: базовый и профил. уровни».- М.: Просвещение, 2010 г. Алгебра и начала мат.анализа: дидакт материалы для 10 кл.: базовый и профил. уровни/ М.К. Потапов, А.В. Шевкин - М.: Просвещение, 2010 г. Экранно – звуковые пособия. Виртуальная школа Кирилла и Мефодия. Технические средства обучения: компьютер, проектор; экран. Учебник для 10-11 классов общеобразоват. учреждений «Алгебра и начала анализа» под ред. А.Н. Колмогорова - М.: Просвещение, 2007 г. рекомендован министерством образования РФ.
|
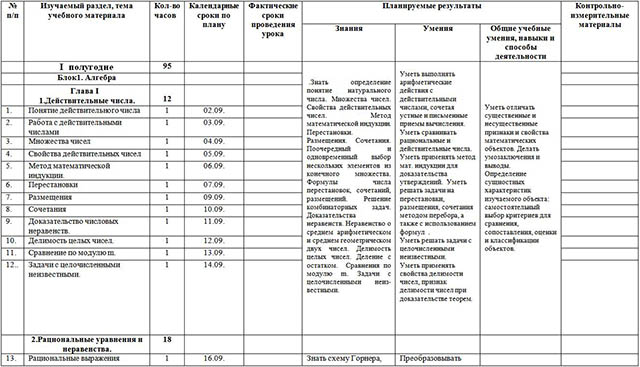

 Получите свидетельство
Получите свидетельство Вход
Вход


 .Корень степени n1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Корень степени n из натурального числа.
.Корень степени n1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Корень степени n из натурального числа. 








 Рабочая программа по предмету "Математика" (10 класс) (0.11 MB)
Рабочая программа по предмету "Математика" (10 класс) (0.11 MB)
 0
0 1574
1574 119
119 Нравится
0
Нравится
0







