Пояснительная записка
Рабочая программа предмета «Математика» для 9 класса на 2015 – 2016 учебный год составлена на основе нормативных документов:
Федеральный закон «Об образовании в Российской Федерации» от 29.12.2012г. № 273-ФЗ.
Федерального компонента государственного стандарта общего образования (приказ МО РФ от 05.03.2004 №1089 (ред.31.12.2012))
Федерального БУП для общеобразовательных учреждений РФ (приказ МО РФ от 09.03.2004 №1312);
Примерной программы для основного общего образования по математике (письмо Департамента государственной политики в образовании Минобрнауки России от 07.07.2005г. № 03-1263 «О примерных программах по учебным предметам Федерального базисного учебного плана» ;
Закона Республики Татарстан от 22.07.2013 № 68-ЗРТ «Об образовании»;
Закона Республики Татарстан от 08.07.1992 № 1560-XII «О государственных языках Республики Татарстан и других языках в Республике Татарстан»;
приказ МО и Н РТ «Об утверждении методических рекомендаций по проектированию содержания организационного раздела основной образовательной программы основного общего образования для общеобразовательных организаций Республики Татарстан», от августа 2015 года;
Приказ Министерства образования и науки РФ от 19\12.2012г. № 1067 «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию на 2013/2014 учебный год».
Приказ Министерства образования и науки РФ от 31.03.2014г. № 253 «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию».
Устава МБОУ «Гимназия №2» имени Баки Урманче Нижнекамского муниципального района РТ
Основной образовательной программы основного общего образования МБОУ «Гимназия №2» имени Баки Урманче Нижнекамского муниципального района РТ (приказ МБОУ «Гимназия №2» НМР РТ № 338 от 01.06.2015)
Учебного плана МБОУ «Гимназия №2» имени Баки Урманче Нижнекамского муниципального района РТ на 2015-2016 учебный год с учётом регионального компонента
Положение о порядке разработки рабочей программы по учебному предмету на 2015-2016 учебный год (приказ МБОУ «Гимназия №2» НМР РТ №323 от 30.05.2015)
Назначение программы: Для обучающихся и родителей (законных представителей) 9 классов МБОУ «Гимназия №2» НМР РТ данная программа обеспечивает реализацию их права на информацию об объеме учебных услуг по математике в этих классах, права на выбор этих услуг и права на гарантию качества получаемых услуг.
- Для педагогического коллектива МБОУ «Гимназия №2» НМР РТ данная программа определяет приоритеты в содержании математического образования в этих классах и способствует интеграции и координации деятельности педагогов в учебном процессе.
- Для муниципального органа управления образованием данная программа является основанием для определения качества реализации определенного объёма гарантированных учебных услуг по математике в 9 классах МБОУ «Гимназия №2» НМР РТ.
Школьное образование в современных условиях призвано обеспечить функциональную грамотность и социальную адаптацию обучающихся на основе приобретения ими компетентностного опыта в сфере учения, познания, профессионально-трудового выбора, личностного развития, ценностных ориентаций. Это предопределяет направленность целей обучения на формирование компетентной личности, способной к жизнедеятельности и самоопределению в информационном обществе, ясно представляющей свои потенциальные возможности, ресурсы и способы реализации выбранного жизненного пути
Целью изучения курса математики в 9 классе является развитие вычислительных и формально - оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов, усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников,систематическое изучение свойств геометрических фигур на плоскости, формирование пространственных представлений, развитие логического мышления и подготовка аппарата, необходимого для изучения курса стереометрии в старших классах. Создание условия для интегрирования в личный опыт новую, в том числе самостоятельно полученную информацию.
В Федеральном базисном плане на изучение математики отводится 5 часов в неделю. Согласно действующему в гимназии учебному плану на изучение математики в 9 классе отводится 170 часов из расчета 5 ч в неделю. Программа соответствует федеральному компоненту государственного стандарта основного общего образования.
Характеристика класса. Основная масса обучающихся 9 – это дети со средним и низким уровнем способностей и невысокой мотивацией учения, которые в состоянии освоить программу по предмету только на базовом уровне. Они отличаются слабой организованностью, часто безответственным отношением к выполнению учебных заданий.
Результаты итоговой контрольной работы показали, что учащиеся допустили ошибки по темам: Системы двух линейных уравнений с двумя переменными. Решение текстовых задач. Равнобедренные и равносторонние треугольники: свойства и признаки равнобедренного треугольника. Учитывая это обстоятельство, на повторение этих тем отводится 4 часа
Содержание программы.
Неравенства и системы неравенств (13часов ,из них контрольные работы-1ч)
Рациональные неравенства и их системы .Линейные и квадратные неравенства (повторение).
Рациональное неравенство. Линейные неравенства с одной переменной. Квадратные неравенства. Метод интервалов. Использование графиков при решении квадратных неравенств. Множества и операции над ними. Элементы множества, подмножество. Объединение и пересечение множеств. Диаграмма Эйлера. Система неравенств. Решение системы неравенств. Примеры решения дробно –линейных неравенств.
Векторы (12 часов,из них контрольные работы-1ч)
Понятие вектора. Длина(модуль) вектора. Равенство векторов. Операции над векторами. Сумма двух векторов. Законы сложения векторов. Правило параллелограмма. Сложение и вычитание векторов. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Координаты вектора. Простейшие задачи в координатах. Применение векторов и координат при решении задач. Средняя линия трапеции.
Координаты (11 часов, из них контрольные работы-1ч)
Декартовы координаты на плоскости, координаты точки. Координаты вектора. Разложение вектора по двум неколлинеарным векторам. Координаты середины отрезка. Связь между координатами вектора и координатами его начала и конца .Формула расстояния между двумя точками плоскости. Координаты суммы, разности и произведения вектора на число. Простейшие задачи в координатах. Уравнение окружности с центром в начале координат и в любой заданной точке. Уравнение окружности. Уравнение прямой. Уравнение прямой, угловой коэффициент прямой, условие параллельности прямой. Использование уравнений окружности и прямой при решении задач. Применение метода координат к решению задач.
Системы уравнений(16часов,из них контрольные работы-1ч)
Основные понятия .Уравнение с двумя переменными. Решение уравнения с двумя переменными. Системы уравнений .График уравнения с двумя переменными. Решение системы. Решение подстановкой . Решение алгебраическим сложением. Метод введения новой переменной. Графическая интерпретация уравнений с двумя переменными и их систем, неравенств с двумя переменными и их систем. Три этапа математического моделирования. Решение текстовых задач алгебраическим способом (Решение задач на совместную работу). Системы уравнений как математические модели реальных ситуаций. Примеры решения нелинейных систем уравнений. Равносильность систем уравнений. Уравнение с несколькими переменными. Примеры решения нелинейных систем. Примеры уравнений высших степеней.
Зависимость между величинами сторон и углов треугольника(14 часов , из них контрольные работы-1ч)
Синус, косинус и тангенс ,котангенс острого угла прямоугольно и углов от 0 до 180°. Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс и котангенс одного и того же угла. Приведение к острому углу. Решение прямоугольных треугольников.
Формулы для вычисления координат точки. Формула, выражающая площадь треугольника: через две стороны и угол между ними. Теоремы синусов и косинусов. Решение треугольников. Угол между векторами. Операции над векторами. Скалярное произведение векторов и его применение в геометрических задачах.
Числовые функции.(25часа из них контрольные работы-1ч)
Понятие функции. Область определения функции. Область значений функции. График функции. Кусочно-заданные функции. Способы задания функции (аналитический, графический, табличный, словесный). Свойства функций (монотонность, ограниченность, выпуклость, наибольшее и наименьшее значения, непрерывность). Четные и нечетные функции. Чтение графиков функции. Степенная функция с натуральным показателем, ее свойства и график. Степенная функция с отрицательным целым показателем, ее свойства и график. Чтение графиков функции.
Функция у =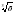 ее свойства и график. Использование графиков функций для решения уравнений, неравенств и систем. Примеры графических зависимостей, отражающих реальные процессы: колебание, показательный рост. Числовые функции, описывающие эти процессы. Параллельный перенос графиков функций вдоль осей координат и симметрия относительно осей.
ее свойства и график. Использование графиков функций для решения уравнений, неравенств и систем. Примеры графических зависимостей, отражающих реальные процессы: колебание, показательный рост. Числовые функции, описывающие эти процессы. Параллельный перенос графиков функций вдоль осей координат и симметрия относительно осей.
Длина окружности и площадь круга (12часов, из них контрольные работы-1ч).
Правильные многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Вписанные и описанные окружности правильного многоугольника. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. Формулы, выражающие площадь треугольника через периметр и радиус вписанной окружности. Вписанные и описанные четырехугольники.
Площадь четырехугольника. Длина окружности. Длина окружности, число π; и длина дуги окружности. Площадь круга и кругового сектора.
Числовые последовательности.(16 часов, из них контрольные работы-1ч)
Числовая последовательность. Способы задания числовых последовательностей. (аналитический, словесный, рекуррентный). Ограниченность и монотонность последовательности .Свойства числовых последовательностей.
Арифметическая прогрессия. Формула n-го члена. Формула суммы членов конечной арифметической прогрессии. Характеристическое свойство. Геометрическая прогрессия. Формула n-го члена. Формула суммы членов конечной геометрической прогрессии. Бесконечно убывающая геометрическая прогрессия
Представление бесконечной периодической дроби в виде обыкновенной .Характеристическое свойство геометрической прогрессии
Геометрические преобразование (7часов, из них контрольные работы-1ч)
Примеры движений фигур. Понятие движения .Отображение плоскости на себя. Симметрия фигур. Осевая и центральная симметрии. Параллельный перенос. Поворот. Наложения и движения. Понятие о гомотетии.
Начальные сведения из стереометрии(5часов)
Правильные многогранники
Наглядные представления о пространственных телах: куб, параллелепипед, призма, пирамида, шар, цилиндр, конус
Примеры сечений
Объём тела. Формулы объёма прямоугольного параллелепипеда, куба.
Формулы объёма шара, цилиндра, конуса
Элементы комбинаторики, статистики и теории вероятностей (12 час, из ни контрольные работы-1ч)
Примеры решения комбинаторных задач.
Перебор вариантов Комбинаторные задачи. Правило умножения. Факториал. Перестановки. Размещения. Сочетания. Представление данных в виде диаграмм, таблиц, виде графиков. Понятие о статистическом выводе на основе выборки. Средние результатов измерений. Частота события. Вероятность. Понятие и примеры случайных событий
Равновозможные события и подсчёт их вероятности
Вероятность суммы несовместных событий.
Случайные события и их вероятность. Вероятность. Событие (случайное, достоверное, невозможное) . Представление о геометрической вероятности
Представление о геометрической вероятности..
Обобщающее повторение(27, из них контрольные работы-2ч (вводная и итоговая)
Требования к уровню подготовки учащихся 9 класса
В результате изучения курса алгебры 9-го класса учащиеся должны уметь:
решать линейные и квадратные неравенства с одной переменной, дробно-рациональные неравенства, неравенства, содержащие модуль;
понимать простейшие понятия теории множеств, задавать множества, производить операции над множествами;
решать системы линейных и квадратных неравенств, системы рациональных неравенств, двойные неравенства;
решать системы уравнений, простые нелинейные системы уравнений двух переменных различными методами;
применять графический метод, метод подстановки, метод алгебраического сложения и метод введения новой переменной при решении практических задач;
составлять математические модели реальных ситуаций и работать с составленной моделью;
исследовать функцию на монотонность, определять наибольшее и наименьшее значение функции, ограниченность, выпуклость, четность, нечетность, область определения и множество значений;
понимать содержательный смысл важнейших свойств функции; по графику функции отвечать на вопросы, касающиеся её свойств;
описывать свойства изученных функций, строить их графики;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
решать простейшие комбинаторные и вероятностные задачи.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
В результате изучения курса геометрии 9-го класса учащиеся должны уметь:
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразование фигур;
вычислять значения геометрических величин (длин, углов, площадей), в том числе: определять значение тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них; находить стороны, углы и площади треугольников, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задания, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве.
Учебно-методический комплект.
Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений / А.Г
Мордкович, П.В Семенов. - 10-е изд. стер. - М.: Мнемозина, 2007.
Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для общеобразовательных учреждений/
[А.Г.Мордкович, Л.А Александровна, Т.Н. Мишустина и др.]; под ред. А.Г. Мордкович-
10-еизд.стер.- М.: Мнемозина, 2007.
Мордкович А.Г. Алгебра. 7-9 кл.: Методическое пособие для учителя. - 3-е изд. -
М.:Мнемозина, 2009.
Алгебра: Тесты для 7-9 кл. общеобразоват. учреждений/ А.Г. Мордкович, Е.Е.
Тульчинская.5-е изд. - М.: Мнемозина. 2006.
Алгебра. 9 класс. Самостоятельные работы для учащихся общеобразовательных учреждений/Л.А. Александрова; под ред. А.Г. Мордковича. - 2-е изд., перераб. и доп. - М.: Мнемозина, 2012.
Алгебра. 9 класс. Контрольные работы для учащихся общеобразовательных
учреждений/Л.А.Александрова; под ред. А.Г. Мордковича. - М.: Мнемозина, 2012.
Геометрия, 7-9: Учеб.дляобщеобразоват. учреждений/ Л.С. Атанасян, В.Ф. Бутузов, СБ.
Кадомцев и др. - М.: Просвещение, 2009
8. Геометрия. Дидактические материалы. 9 класс/ Б.Г. Зив- М: Просвещение, 2009
9. Математика. Самостоятельные и контрольные работы.9класс./А.П.Ершова, В,В,Голобородько, А.С.Ершова-М”Илекса”2004
10. Тематический контроль по геометрии к учебнику Л .С.Атанасяна и др.9 класс/Мельников Н.Б. Лепихова Н. М.-М “Интеллект-центр”2009
11. Геометрия. 9 класс: Поурочные планы (по учебнику Л.С. Атанасяна и др. Геометрия 7-9)/
авт.-сост. М.Г.Гилярова. - Волгоград: Учитель - АСТ, 2003
12. Гаврилова Н.Ф. Поурочные разработки по геометрии: 9 класс. - М.:ВАК0,2004.
Учебно-тематическое планирование
| Тема урока | Кол-во уроков |
| Повторение.Действия с алгебраическими дробями. Алгебраические дроби .Сокращение дробей Квадратное уравнение. Решение рациональных уравнений. Неравенства и их свойства. Системы двух линейных уравнений с двумя переменными. Решение текстовых задач. Равнобедренные и равносторонние треугольники: свойства и признаки равнобедренного треугольника. | 5 |
| Повторение.. Нулевой к\срез | 1 |
| Линейные и квадратные неравенства. Решение неравенств. | 2 |
| Квадратные неравенства. Использование графиков при решении квадратных неравенств | 1 |
| Квадратные неравенства.Метод интервалов | 3 |
| Примеры решения дробно–линейных неравенств | 2 |
| Элемент множества, подмножество. Множества и операции над ними.Объединение и пересечение множеств. Диаграммы Эйлера. Множества и операции над ними.
| 2 |
| Линейные неравенства с одной переменной и их системы. Квадратные неравенства. | 2 |
| Контрольная работа №1.«Линейные неравенства с одной переменной и их системы. Квадратные неравенства» | 1 |
| Повторение. Теорема Пифагора. Медиана, биссектриса и высота треугольника .Четырехугольники. | 2 |
| Понятие вектора, длина, модуль вектора, Равенство векторов. | 2 |
| Операции над векторами. Сумма двух векторов. Законы сложения векторов. Правило параллелограмма | 1 |
| Операции над векторами. Вычитание векторов | 1 |
| Операции над векторами.Сумма нескольких векторов | 1 |
| Операция над векторами:умножение на число | 1 |
| Операции над векторами. Применение векторов к решению задач | 2 |
| Операции над векторами.Средняя линия трапеции | 2 |
| Контрольная работа №2 “Векторы” | 1 |
| Декартовы координаты на плоскости, координаты точки.Координаты вектора.Разложение вектора по двум неколлинеарным векторам. | 1 |
| Связь между координатами вектора и координатами его начала и конца.Координаты середины отрезка | 1 |
| Формула расстояния между двумя точками плоскости | 1 |
| Уравнение окружности с центром в начале координат и в любой заданной точке. | 2 |
| Уравнение прямой,угловой коэффициент прямой,условие параллельности прямых | 2 |
| Формула расстояния между точками координатной прямой. Координатный метод при решении задач | 1 |
| Решение задач.Уравнение окружности с центром в начале координат и в любой заданной точке. Уравнение прямой Подготовка к к.р. по теме “Метод координат» | 2 |
| Контрольная работа №3 по теме «Координаты» | 1 |
| Основные понятия. Уравнение с двумя переменными. Решение уравнения с двумя переменными
| 1 |
| Система уравнений. Решение системы. Основные понятия. График уравнения с двумя переменными. | 1 |
| Решение системы. Решение подстановкой.
| 1 |
| Методы решения систем уравнений. Решение алгебраическим сложением | 1 |
| Метод подстановки. Решение системы. Метод введения новой переменной | 1 |
| Система уравнений; решение системы. | 1 |
| Метод введения новых переменных. Метод замены переменой. Решение системы. Методы решения систем уравнений. | 1 |
| Графическая интерпретация уравнений с двумя переменными и их систем, неравенств с двумя переменными и их систем | 1 |
| Система уравнений; решение системы. Решение текстовых задач алгебраическим способом.(Системы уравнений как математические модели реальных ситуаций). Примеры решения нелинейных систем уравнений | 3 |
| Три этапа математического моделирования. Уравнение с несколькими переменными. | 1 |
| Уравнение с несколькими переменными | 1 |
| Система уравнений; решение системы. Примеры решения уравнений в целых числах Системы уравнений как математические модели реальных ситуаций Примеры решения нелинейных систем уравнений | 1 |
| Примеры уравнений высших степеней | 1 |
| Контрольная работа №4 по теме «Системы уравнений» | 1 |
| Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника и углов от 0° до 180°. Основное тригонометрическое тождество. | 1 |
| Формулы, связывающие синус, косинус, тангенс и котангенс одного и того же угла. Приведение к острому углу | 1 |
| Решение прямоугольных треугольников.Формулы для вычисления координат точки | 1 |
| Формула, выражающая площадь треугольника: через две стороны и угол между ними | 1 |
| Теорема косинусов.Теорема синусов. | 1 |
| Измерительные работы.Теорема синусов и теорема косинусов; примеры их применения для вычисления элементов треугольника | 4 |
| Угол между векторами. | 1 |
| Операции над векторами. Скалярное произведение векторов. | 2 |
| Решение задач по теме “Соотношения между сторонами и углами треугольника” | 1 |
| Контрольная работа №5 по теме: «Зависимость между величинами сторон и углов треугольника».
| 1 |
| Понятие функции. Область определения. Область определения функции | 2 |
| Кусочно-заданные функции.Способы задания функций. График функции | 1 |
| График функции, возрастание и убывание функции нули функции | 1 |
| График функции. Наибольшее и наименьшее значение, ограниченность, выпуклость и непрерывность функции.. | 1 |
| Чтение графиков функций. Свойства функций. | 1 |
| Свойства функций.Чтение графиков функции. Промежутки знакопостоянства | 1 |
| Чтение графиков функции. Четные и нечетные функции | 2 |
| Степенные функции с натуральным показателем, их графики | 3 |
| Степенные функции с натуральным показателем, их графики. Функции y = x–n (nN), их свойства и графики. | 2 |
| Использование графиков функций для решения уравнений, неравенств и систем. | 2 |
| График функции: корень кубический; свойства. | 3 |
| Примеры графических зависимостей, отражающих реальные процессы: колебание, показательный рост. Числовые функции, описывающие эти процессы | 1 |
| Параллельный перенос графиков функций вдоль осей координат и симметрия относительно осей.
| 1 |
| Контрольная работа №7 по теме «Степенные функции с натуральным показателем, их графики». | 1 |
| Правильные многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника | 1 |
| Вписанные и описанные окружности правильного многоугольника. | 1 |
| Вписанные и описанные многоугольники. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. Формулы, выражающие площадь треугольника через периметр и радиус вписанной окружности Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. Формулы, выражающие площадь треугольника через периметр и радиус вписанной окружности Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности | 1 |
| Вписанные и описанные окружности правильного многоугольника.Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. | 1 |
| Вписанные и описанные четырехугольники.Площадь четырехугольника | 1 |
| Длина окружности | 1 |
| Длина окружности, число π; и длина дуги окружности. | 1 |
| Площадь круга. Площадь кругового сектора. | 3 |
| Длина окружности. Площадь круга | 1 |
| Контрольная работа №4 по теме: “Длина окружности и площадь круга” | 1 |
| Понятие последовательности.Ограниченность и монотонность последовательности. | 1 |
| Понятие последовательности. Числовые последовательности | 1 |
| Арифметическая прогрессия. Формула общего члена арифметической прогрессии, формула суммы первых нескольких членов арифметической прогрессии. | 3 |
| Арифметическая прогрессия. Характеристическое свойство | 2 |
| Геометрическая прогрессия. Формулы общего члена геометрической прогрессии, суммы нескольких членов геометрической прогрессии | 2 |
| Геометрическая прогрессия.Бесконечно убывающая геометрическая прогрессия.Представление бесконечной периодической дроби в виде обыкновенной | 1 |
| Геометрическая прогрессия. Характеристическое свойство | 2
|
| Геометрическая прогрессия. Сложные проценты | 1 |
|
|
|
| Арифметическая и геометрическая прогрессии |
|
| Контрольная работа №9 по теме «Числовые последовательности» | 1 |
| Примеры движений фигур. Понятие движения.Понятие движения. Наложения и движения | 1 |
| Симметрия фигур. Осевая симметрия и параллельный перенос. | 1 |
| Параллельный перенос. | 1 |
| Поворот и центральная симметрия. | 1 |
| Параллельный перенос. Поворот | 1 |
| Симметрия фигур. Параллельный перенос. Поворот | 1 |
| Понятие о гомотетии | 1 |
| Контрольная работа №5 по теме “Геометрические преобразования” | 1 |
| Примеры решения комбинаторных задач. Перебор вариантов | 1 |
| Примеры решения комбинаторных задач. Правило умножения | 2 |
| Представление данных в виде диаграмм, таблиц | 1 |
| Представление данных в виде графиков | 1 |
| Понятие о статистическом выводе на основе выборки. Средние результаты измерений | 1 |
| Частота события. Вероятность. Понятие и примеры случайных событий | 1 |
| Равновозможные события и подсчёт их вероятности | 1 |
| Вероятность суммы несовместных событий | 1 |
| Случайные события и их вероятность. | 1 |
| Представление о геометрической вероятности | 2 |
| Контрольная работа № 12 по теме «Элементы статистики и теории вероятностей» | 1 |
| Правильные многогранники | 1 |
| Наглядные представления о пространственных телах: куб, параллелепипед, призма, пирамид, шар, цилиндр. конус | 1 |
| Примеры сечений | 1 |
| Объём тела. Формулы объёма прямоугольного параллелепипеда, куба | 1 |
| Формулы объёма шара, цилиндра, конуса. Аксиомы планиметрии | 1 |
| Повторение. Итоговая контрольная работа | 19 |
Требования к уровню подготовки учащихся 9 классов
Учащиеся должны знать/понимать:
– значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
– значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
– универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности; вероятностный характер различных процессов окружающего мира;
должны уметь:– выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
– составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
– выполнять основные действия со степенями с целыми показателями, с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
– применять свойства арифметических квадратов корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
– решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные уравнения;
– решать линейные и квадратные неравенства с одной переменной и их системы;
– решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
– изображать числа точками на координатной прямой;
– определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
– распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
– находить значения функции, заданной формулой, таблицей, графиком по её аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;
– определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
– описывать свойства изученных функций, строить их графики;
– извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
– решать комбинаторные задачи путём систематического перебора возможных вариантов и с использованием правила умножения;
– вычислять средние значения результатов измерений;
– находить частоту события, используя собственные наблюдения и готовые статистические данные;
– находить вероятности случайных событий в простейших случаях;
владеть компетенциями: познавательной,коммуникативной, информационной и рефлексивной;
решать следующие жизненно-практические задачи: – самостоятельно приобретать и применять знания в различных ситуациях;
– работать в группах;
– аргументировать и отстаивать свою точку зрения;
– уметь слушать других; извлекать учебную информацию на основе сопоставительного анализа объектов;
– пользоваться предметным указателем энциклопедий и справочников для нахождения информации;
– самостоятельно действовать в ситуации неопределённости при решении актуальных для них проблем.
Уметь пользоваться языком геометрии для описания предметов окружающего мира.
Уметь производить операции над векторами.
Уметь вычислять значения геометрических величин.
Уметь решать геометрические задачи координатным методом.
Уметь проводить доказательные рассуждения при решении задач, используя известные теоремы.
Уметь решать простейшие планиметрические задачи в пространстве.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни.
Уметь производить операции над векторами, вычислять длину и координаты вектора, угол между векторами, скалярное произведение
Уметь вычислять значения геометрических величин, в том числе: для углов от 0о до 180о определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них; находить стороны, углы и площади треугольников.
Уметь решать простейшие планиметрические задачи в пространстве, используя скалярное произведение векторов.
Уметь решать комбинаторные задачи с использованием правила умножения.
Уметь находить вероятности случайных событий в простейших случаях.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения учебных и практических задач, требующих систематического перебора вариантов.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией.
Уметь распознавать геометрические фигуры, различать их взаимное расположение.
Уметь изображать геометрические фигуры, выполнять чертежи по условию задачи.
Уметь вычислять длины дуг окружности, длину окружности, периметры и площади правильных многоугольников, площади круга и сектора.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения практических задач, связанных с нахождением геометрических величин(используя при необходимости справочники и технические средства.
Уметь выполнять построения правильных многоугольников
Уметь приводить примеры движения фигур.
Уметь строить фигуры симметричные относительно центра и оси симметрии.
Уметь использовать параллельный перенос и поворот
Учебно-методический комплект
А. Г. Мордкович, Алгебра. 9 класс: учебник для общеобразовательных учреждений / А. Г. Мордкович. - М.: Мнемозина, 2009.
А. Г. Мордкович, Алгебра. 9 класс: задачник для общеобразовательных учреждений. - М.: Мнемозина, 2009.
Л. А. Александрова, Алгебра 9 класс: самостоятельные работы для общеобразовательных учреждений. - М.: Мнемозина, 2009.
А. Г. Мордкович, Е. Е. Тульчинская Алгебра: тесты для 7-9 классов общеобразовательных учреждений. - М.: Мнемозина, 2009.
Ю. П. Дудницын, Е. Е. Тульчинская Алгебра. 9 класс: контрольные работы для общеобразовательных учреждений. - М.: Мнемозина, 2009.
6.Атанасян Л. С. Геометрия. 7 – 9. ( текст ) / Л. С. Атанасян, В. Ф. Бутузов. – М.: Просвещение, 2009.
.
8.Атанасян Л. С. Изучение геометрии в 7 – 9 классах: методические рекомендации для учителя ( текст ) / Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков и др. – М.: Просвещение, 2007.
9.Зив Б. Г. Дидактические материалы по геометрии для 9 кл. ( Текст ) / Б. Г. Зив, В. М. Мейлер. – М.: Просвещение, 2007.
А также дополнительных пособий для учащихся:
1. Кузнецова, Л. В. Сборник заданий для проведения письменного экзамена по алгебре за курс средней школы. 9 класс / Л. В. Кузнецова и др. – М.: Дрофа, 2004.
2. Шестаков, С. А. Сборник задач для подготовки и проведения письменного экзамена по алгебре за курс основной школы: 9 класс / С. А. Шестаков. – М.: АСТ: Астрель, 2006.
3. Лысенко, Ф. Ф. Предпрофильная подготовка итоговой аттестации / Ф. Ф. Лысенко. – Ростов н/Д.: Легион, 2006; 2007; 2008.
4. Кузнецова, Л. В. Сборник заданий для подготовки к итоговой аттестации в 9 классе / Л. В. Кузнецова, С. Б. Суворова. – М.: Просвещение, 2007.
ля учителя:
11. Клименченко, Д. В. Задачи по математике для любознательных / Д. В. Клименченко. – М.: Просвещение, 2007.
12. Мордкович, А. Г. Алгебра. 7–9 классы: методическое пособие для учителей / А. Г. Мордкович. – М.: Мнемозина, 2004.
13. Арутюнян, Е. Б. Математические диктанты для 5–9 классов / Е. Б. Арутюнян. – М., 1995.
14. Пичурин, Л. Ф. За страницами учебника алгебры / Л. Ф. Пичурин. – М., 1990.
15. Заболотнева, Н. В. Олимпиадные задания по математике: 5–8 классы / Н. В. Заболотнева. – Волгоград: Учитель, 2006.
16. Лысенко, Ф. Ф. Учебно-тренировочные тестовые задания «малого» ЕГЭ по математике / Ф. Ф. Лысенко. – Ростов н/Д.: Легион, 2008.
18. Арутюнян, Е. Б. Математические диктанты для 5–9 классов / Е. Б. Арутюнян. – М., 1995.
19. Математика: еженедельное приложение к газете «Первое сентября».
20. Математика в школе: ежемесячный научно-методический журнал.
Календарно – тематическое планирование
| № урока | Тема урока | Кол-во часов | Планируемые результаты освоения материала | Дата по плану | Дата по факту |
Неравенства и их системы (15)
| 1 | Повторение. Действия с алгебраическими дробями. Квадратное уравнение. Решение рациональных уравнений. Примеры решения уравнений высших степеней. | 1 | Знать понятие линейного и квадратного неравенств с одной переменной. Уметь решать линейные и квадратные неравенства с одной переменной и содержащие модуль. |
|
|
| 2 | Повторение. Квадратичная функция. Графики функций: корень квадратный, модуль. Решение неравенств.
| 1 | Знать понятие равносильность неравенств линейного и квадратного неравенства, алгоритмы их решения, знака объединения множеств. Уметь решать линейные и квадратные неравенства. |
|
|
| 3 |
Повторение. Нулевой к\срез. | 1 | Знать понятие линейного и квадратного неравенства, алгоритмы их решения, знака объединения множеств. Уметь решать системы простых рациональных неравенств методом интервалов. |
|
|
| 4 | Линейные и квадратные неравенства. Решение неравенств. | 1 | Знать понятие рациональных неравенств. Уметь решать рациональных неравенств |
|
|
| 5 | Линейные и квадратные неравенства. Решение неравенств. | 1 | Знать понятие дробно- линейных и квадратных неравенств с одной переменной. Уметь решать линейные и квадратные неравенства с одной переменно и содержащие модуль. |
|
|
| 6 | Квадратные неравенства. Использование графиков при решении квадратных неравенств. | 1 | Знать решение рациональных неравенств методом интервалов. Уметь решать дробно-рациональные неравенства методом интервалов. |
|
|
| 7 | Квадратные неравенства. Метод интервалов используя графики. | 1 | Знать решение рациональных неравенств используя графики, применять правила равносильного преобразования неравенств. Уметь решать неравенства используя графики. |
|
|
| 8 | Квадратные неравенства. Метод интервалов | 1 | Знать о способах решения систем рациональных неравенств. Уметь решать двойные неравенства; системы простых рациональных неравенств методом интервалов; объяснить изученные положения на самостоятельно подобранных конкретных примерах; извлекать необходимую информацию из учебно-научных текстов. |
|
|
| 9 | Квадратные неравенства. Метод интервалов | 1 | Знать о способах решения систем рациональных неравенств. Уметь решать двойные неравенства; системы простых рациональных неравенств методом интервалов. |
|
|
| 10 | Примеры решения дробно – линейных неравенств | 1 | Знать о способах решения систем рациональных неравенств. Уметь раскрывать знак модуля; решать двойные неравенства; решать системы простых рациональных неравенств методом интервалов. |
|
|
| 11 | Элемент множества, подмножество. Множества и операции над ними. Объединение и пересечение множеств. Диаграммы Эйлера. Множества и операции над ними. | 1 | Знать о способах решения систем рациональных неравенств. Уметь раскрывать знак модуля; решать двойные неравенства; решать системы простых рациональных неравенств методом интервалов. |
|
|
| 12 | Контрольная работа №1 по теме «Линейные неравенства с одной переменной и их системы. Квадратные неравенства» | 1 | Уметь самостоятельно применять полученные теоретические знания на практике |
|
|
| 13 | Работа над ошибками по теме «Линейные неравенства с одной переменной и их системы. Квадратные неравенства» | 1 | Уметь анализировать ошибки, допущенные в контрольной работе, знать правильное решение заданий .Уметь решать рациональные неравенства и системы рациональных неравенств; владеть навыками самоанализа и самоконтроля |
|
|
| 14 | Повторение. Окружность, вписанная в треугольник. | 1 | Знать понятие вписанной окружности, теорему о вписанной окружности в треугольник, четырехугольник. Уметь доказывать теоремы, решать задачи. |
|
|
| 15 | Повторение. Окружность, описанная около треугольника. | 1 | Знать понятие вписанной окружности, теорему о вписанной окружности в треугольник, четырехугольник. Уметь доказывать теоремы, решать задачи. |
|
|
Векторы. Координаты (19 уроков)
| 16 | Понятие вектора, длина, модуль вектора,коллинеарные векторы. | 1 | Знатьпонятие вектора и модуль вектора Уметстроить векторы и найти модуль вектора |
|
|
| 17 | Вектор. Равенство векторов | 1 | Знать понятие вектора, равенство векторов. Уметь строить равные векторы находить координаты вектора. |
|
|
| 18 | Операции над векторами. Сумма двух векторов. Законы сложения векторов. Правило параллелограмма | 1 | Знать правила сложения векторов. Уметь строить векторы, складывать векторы.
|
|
|
| 19 | Операции над векторами. Вычитание векторов | 1 | Знатьпонятие вектора, правила вычитания векторов. Уметь строить векторы и вычитать векторы. |
|
|
| 20 | Операции над векторами. Сумма нескольких векторов. | 1 | Знать понятие вектора, правила сложения, вычитания векторов. Уметь строить векторы, складывать и вычитать векторы. |
|
|
| 21 | Операция надвекторами:умножение на число | 1 | Знать понятие вектора, , правило умножения вектора на число. Уметь строить векторы. |
|
|
| 22 | Операции над векторами. Применение векторов к решению задач | 1 | Знать основные свойства произведения вектора на число Уметь решатьпростейшие задачи напроизведения вектора на число. |
|
|
| 23 | Операции над векторами. Применение векторов к решению задач | 1 | Знать понятие вектора, правила сложения, вычитания векторов, правило умножения вектора на число. Уметь строить векторы, складывать и вычитать векторы, строить равные векторы, решать простейшие задачи. |
|
|
| 24 | Операции над векторами.Средняя линия трапеции | 1 | Знать понятие средняя линия трапеции Уметь строить векторы, складывать и вычитать векторы, строить равные веторы находить координаты вектора, решать простейшие задачи Подготовка к к.р. “Векторы”. |
|
|
| 25 | Контрольная работа №2 “Векторы” | 1 | Уметь самостоятельно применять полученные теоретические знания на практике. |
|
|
| 26 | Работа над ошибками по теме “Векторы”. | 1 | Уметь анализировать ошибки, допущенные в контрольной работе, знать правильное решение заданий.Проводить доказательные рассуждения в ходе решение задач. |
|
|
| 27 | Декартовы координаты на плоскости, координаты точки.Координаты вектора. Разложение вектора по двум неколлинеарным векторам | 1 | Знать понятие угол между векторами, понятие координаты вектора. Уметь строить равные веторы находить координаты вектора. |
|
|
| 28 | Связь между координатами вектора и координатами его начала и конца.Координаты середины отрезка | 1 | Знать связь между координатами вектора и координатами его начала и конца. Уметь строить векторы, решать простейшие задачи в координатах,связь между координатами вектора и координатами его начала и конца. |
|
|
| 29 | Формула расстояния между двумя точками плоскости | 1 | Знать правило разложения вектора по двум неколлинеарным векторам. Уметь строить векторы, складывать и вычитать векторы, строить равные веторы находить координаты вектора, решать простейшие задачи в координатах. |
|
|
| 30 | Уравнение окружности с центром в начале координат и в любой заданной точке. | 1 | Знать понятие уравнение окружности. Уметь составлять уравнение окружности |
|
|
| 31 | Уравнение прямой,угловой коэффициент прямой,условие параллельности прямых | 1 | Знать понятие уравнение прямой Уметь составлять уравнение прямой, |
|
|
| 32 | Решение задач.Уравнение окружности с центром в начале координат и в любой заданной точке. Уравнение прямой Подготовка к к.р. “Метод координат | 1 | Демонстрация учащимися знаний и умений по теме «Векторы. Метод координат» |
|
|
| 33 | Контрольная работа №3 по теме «Координаты» | 1 | Уметь самостоятельно применять полученные теоретические знания на практике. |
|
|
| 34 | Работа над ошибками по темеУравнение прямой, угловой коэффициент, условие параллельности прямых.Координатный метод при решении задач | 1 | Уметь анализировать ошибки, допущенные в контрольной работе, знать правильное решение заданий.Уметь самостоятельно применять полученные теоретические знания на практике. |
|
|
Системы уравнений (15 уроков )
| 35 | Основные понятия. Уравнение с двумя переменными. Решение уравнения с двумя переменными. | 1 | Знать понятие решения уравнения в целых числах. Уметь решать уравнения в целых числах. |
|
|
| 36 | Система уравнений. Решение системы. Основные понятия. График уравнения с двумя переменными. | 1 | Знать понятие рациональные уравнения с двумя переменными. Уметь решать рациональные уравнения с двумя переменными. |
|
|
| 37 | Решение системы Решение подстановкой.
| 1 | Знать формулу расстояния между двумя точками координатной плоскости. Уметь применять при решении формулу расстояния между двумя точками координатной плоскости. |
|
|
| 38 | Методы решения систем уравнений. Решение алгебраическим сложением
| 1 | Знать системы уравнений с двумя переменными; методы решения систем уравнений. Уметь решать уравнения с двумя переменными, решать системы уравнений с двумя переменными методом подстановки, методом алгебраического сложения, методом введения новой переменной, графическим методом. |
|
|
| 39 | Метод подстановки. Решение системы. Метод введения новой переменной | 1 | Знать алгоритм метода подстановки. Уметь при решении систем уравнений применять метод подстановки |
|
|
| 40 | Система уравнений; решение системы. | 1 | Знать алгоритм метода алгебраического сложения. Уметь при решении систем уравнений применять метод алгебраического сложения. |
|
|
| 41 | Метод введения новых переменных. Метод замены переменой. Решение системы. Методы решения систем уравнений | 1 | Знать алгоритмы решения систем уравнений. Уметь при решении систем уравнений применять использовать метод замены, метод алгебраического сложения и метод введения новой переменной. |
|
|
| 42 | Графическая интерпретация уравнений с двумя переменными и их систем, неравенства с двумя переменными и их систем. | 1 | Знать алгоритм графического способа решения системы уравнений. Уметь использовать графики при решении системы уравнений. |
|
|
| 43 | Система уравнений; решение системы. Системы уравнений как математические модели реальных ситуаций.Примеры решения нелинейных систем уравнений. | 1 | Знать, как составлять математические модели реальных ситуаций и работать с составленной моделью. Уметь составлять математические модели реальных ситуаций и работать с составленной моделью; приводить примеры, подбирать аргументы, формулировать выводы. |
|
|
| 44 | Три этапа математического моделирования. | 1 | Знать, как составлять математические модели реальных ситуаций и работать с составленной моделью. Уметьсоставлять математические модели реальных ситуаций и работать с составленной моделью; приводить примеры, подбирать аргументы, формулировать выводы. |
|
|
| 45 | Задачи на движение по реке и на производительность | 1 | Знать, как составлять математические модели реальных ситуаций и работать с составленной моделью. Уметь составлять математические модели реальных ситуаций и работать с составленной моделью; приводить примеры, подбирать аргументы, формулировать выводы. |
|
|
| 46 | Система уравнений; решение системы. Системы уравнений как математические модели реальных ситуаций. Примеры решения нелинейных систем уравнений | 1 | Знать, как составлять математические модели реальных ситуаций и работать с составленной моделью. Уметь составлять математические модели реальных ситуаций и работать с составленной моделью; воспроизводить прочитанную информацию с заданной степенью свернутости; аргументировано отвечать на поставленные вопросы, осмыслить ошибки и устранить их. |
|
|
| 47 | Решение задач. Примеры решения уравнений в целых числах. Примеры уравнений высших степеней. | 1 | Знать, как составлять математические модели реальных ситуаций и работать с составленной моделью. Уметь составлять математические модели реальных ситуаций и работать с составленной моделью; приводить пример решения уравнений в целых числах и уравнений высших степеней. |
|
|
| 48 | Контрольная работа №4 по теме «Системы уравнений» | 1 | Уметь самостоятельно применять полученные теоретические знания на практике |
|
|
| 49 | Работа над ошибками по теме«Системы уравнений» | 1 | Уметь анализировать ошибки, допущенные в контрольной работе, знать правильное решение заданий. Знать и уметь владеть навыками самоанализа и самоконтроля |
|
|
Зависимость между величинами сторон и углов треугольника (11 уроков)
| 50 | Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника и углов от 0° до 180°. Основное тригонометрическое тождество. | 1 | Знать понятия синуса, косинуса и тангенса угла, как вычисляется синус, косинус, тангенс для углов от 0 до 180. Уметьдоказывать основное тригонометрическоетождество, знать формулу для вычисления координат точки, уметь решать задачи. |
|
|
| 51 | Формулы, связывающие синус, косинус, тангенс и котангенс одного и того же угла. Приведение к острому углу. | 1 | Знать формулу для вычисления координаты точки. Уметь решать задачи, применяя формулы для вычисления координаты точки. |
|
|
| 52 | Решение прямоугольных треугольников. Формулы для вычисления координат точки | 1 | Знать понятия синуса, косинуса и тангенса угла, формулу для вычисления координаты точки . Уметь решать задачи, применяя формулы для вычисления координаты точки. |
|
|
| 53 | Формула, выражающая площадь треугольника: через две стороны и угол между ними | 1 | Знать понятия синуса, косинуса и тангенса угла, формулу для вычисления координаты точки, теорему синусповУметь решать задачи, применяя формулы для вычисления координаты точки, теоремы синусов |
|
|
| 54 | Теорема косинусов.Теорема синусов. | 1 | Знать понятия синуса, косинуса и тангенса угла, формулу для вычисления координаты точки, теорему синуспов, теорему косинусов. Уметь решать задачи, применяя формулы для вычисления координаты точки, теоремы синусов и косинусов. |
|
|
| 55 | Измерительные работы. Теорема синусов и теорема косинусов; примеры их применения для вычисления элементов треугольника | 1 | Знать теорему о площади треугольника, теоремы синусов и косинусов, измерительные работы, основанные на использовании этих теорем, методы решения треугольников. Уметь решать задачи, строить углы, вычислять координаты точки с помощью синуса, косинуса и тангенса угла, вычислять площадь. |
|
|
| 56 | Угол между векторами. | 1 | Знать теорему о площади треугольника, теоремы синусов и косинусов, измерительные работы, основанные на использовании этих теорем, методы решения треугольников. Уметь решать задачи, строить углы, вычислять координаты точки с помощью синуса, косинуса и тангенса угла, вычислять площадь треугольника по двум сторонам и углу между ними, решать треугольники; объяснять, что такое угол между векторами. |
|
|
| 57 | Операции над векторами. Скалярное произведение векторов. | 1 | Знать теорему о площади треугольника, теоремы синусов и косинусов, измерительные работы, основанные на использовании этих теорем, методы решения треугольников. Уметь решать задачи, строить углы, вычислять координаты точки с помощью синуса, косинуса и тангенса угла, вычислять площадь треугольника по двум сторонам и углу между ними, решать треугольники; объяснять, что такое угол между векторами. |
|
|
| 58 | Свойства скалярного произведения. Подготовка к контрольной работе. Операции над векторами. Скалярное произведение векторов. | 1 | Знать теорему о площади треугольника, теоремы синусов и косинусов, измерительные работы, основанные на использовании этих теорем, методы решения треугольников. Уметь решать задачи, строить углы, вычислять координаты точки с помощью синуса, косинуса и тангенса угла, вычислять площадь треугольника по двум сторонам и углу между ними, решать треугольники; объяснять, что такое угол между векторами. |
|
|
| 59 | Решение задач по теме “Соотношения между сторонами и углами треугольника” | 1 | Демонстрация учащимися знаний и умений по теме «Соотношения между сторонами и углами треугольника» |
|
|
| 60 | Контрольная работа №5 по теме: «Зависимость между величинами сторон и углов треугольника».
| 1 | Уметь анализировать ошибки, допущенные в контрольной работе, знать правильное решение заданий.Уметь самостоятельно применять полученные теоретические знания на практике |
|
|
Числовые функции( 15уроков ).
| 61 | Понятие функции. Область определения. | 1 | Знать определение числовой функции, область определения функции, область значения функции. Уметь находить область определения функции, объяснить изученные положения на самостоятельно подобранных конкретных примерах. |
|
|
| 62 | Область определения функции | 1 | Знать понятия: функция, область определения функции, область значения функции. Уметь находить область определения функции, пользоваться навыками нахождения области определения функции, решая задания повышенной сложности |
|
|
| 63 | Кусочно-заданные функции.Способы задания функций. График функции | 1 | Знать понятия: функция ограниченность функции сверху и снизу, промежутки знакопостоянства функции. Уметь находить область определения кусочно-заданные функции , объяснить изученные положения на самостоятельно подобранных конкретных примерах; . |
|
|
| 64 | График функции, возрастание и убывание функции нули функции | 1 | Иметь представление о свойствах функции: монотонности, наибольшем и наименьшем значении функции, ограниченности, выпуклости и непрерывности.нули функции Уметь исследовать функции на: монотонность, наибольшее и наименьшее значение, ограниченность, выпуклость инепрерывность; отбирать и структурировать материал; аргументировано отвечать на поставленные вопросы, участвовать в диалоге. |
|
|
| 65 | График функции. Наибольшее и наименьшее значение, ограниченность, выпуклость и непрерывность функции.
| 1 | Иметь представление о способах задания функции: аналитическом, графическом, табличном, словесном. Уметь при задании функции применять различные способы: аналитический, графический, табличный, словесный; отбирать и структурировать материал; проводить анализ данного задания, аргументироватьрешение, презентовать решения |
|
|
| 66 | Чтение графиков функций. Свойства функций. | 1 | Иметь представление о способах задания функции: аналитическом, графическом, табличном, словесном. Уметь при задании функции применять различные способы: аналитический, графический, табличный, словесный отбирать и структурировать материал; проводить анализ данного задания, аргументировать решение, презентовать решения |
|
|
| 67 | Свойства функций. Чтение графиков функции. Промежутки знакопостоянства. | 1 | Иметь представление о свойствах функции , чтение графиков функции и промежутки знакопостоянства. Уметь исследовать функции , отбирать и структурировать материал; аргументировано отвечать на поставленные вопросы, участвовать в диалоге |
|
|
| 68 | Чтение графиков функции. Четные и нечетные функции | 1 | Иметь представление о свойствах четных и нечетных функции Уметь исследовать функции на четность и нечетность. |
|
|
| 69 | Чтение графиков функции. Четные и нечетные функции
| 1 | Иметь представление о свойствах функции: монотонности, наибольшем и наименьшем значении функции. Уметь аргументировано отвечать на поставленные вопросы, участвовать в диалоге. |
|
|
| 70 | Наибольшее и наименьшее значение функции. | 1 | Иметь представление о свойствах функции: монотонности, наибольшем и наименьшем значении функции, ограниченности, выпуклости и непрерывности. Уметь исследовать функции на монотонность, наибольшее и наименьшее значение, ограниченность, выпуклость и непрерывность. |
|
|
| 71 | Наибольшее и наименьшее значение функции. | 1 | Иметь представление о свойствах функции: монотонности, наибольшем и наименьшем значении функции, ограниченности, выпуклости и непрерывности. Уметь исследовать функции на монотонность, наибольшее и наименьшее значение, ограниченность, выпуклость и непрерывность; |
|
|
| 72 | Четные и нечетные функции. | 1 | Знать понятие четной и нечетной функции Уметь применять алгоритм исследования функции на четность и нечетность. |
|
|
| 73 | Алгоритм исследования функций. Решение задач по теме: «Способы задания функции» | 1 | Знать об алгоритме исследования функции на четность и нечетность. Уметь применять алгоритм исследования функции начетность и нечетность, строить графики четных и нечетных функций; приводить примеры, подбирать аргументы, формулировать выводы; классифицировать и проводить сравнительный анализ |
|
|
| 74 | Контрольная работа №3 по теме «Способы задания функции. Свойства функций» | 1 | Уметь самостоятельно применять полученные теоретические знания на практике. |
|
|
| 75 | Работа над ошибками .График функции. Наибольшее и наименьшее значение, ограниченность, выпуклость и непрерывность функции.
| 1 | Уметь анализировать ошибки, допущенные в контрольной работе, знать правильное решение заданий. Уметь самостоятельно находить область определения функции, пользоваться навыками нахождения области определения функции, решая задания повышенной сложности |
|
|
Длина окружности и площадь круга (12 уроков)
| 76 | Правильные многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника | 1 | Знать понятие правильного многоугольника Уметь строить правильные многоугольники |
|
|
| 77 | Вписанные и описанные окружности правильного многоугольника | 1 | Знать понятие правильного многоугольника, описанного около него. Уметь строить правильные многоугольники описанные около неё, решать задачи. |
|
|
| 78 | Вписанные и описанные окружности правильного многоугольника. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. | 1 | Знать понятие правильного многоугольника, описанного около него. Уметь строить правильные многоугольники описанные около неё, решать задачи. |
|
|
| 79 | Вписанные и описанные окружности правильного многоугольника.Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. | 1 | Знать понятие правильного многоугольника, окружность, вписанная в правильный многоугольника. Уметь строить правильные многоугольники вписанные в окружность и описанные около неё, решать задачи. |
|
|
| 80 | Вписанные и описанные четырехугольники. Площадь четырехугольника. | 1 | Знать понятие вписанного и описанного четырехугольника. Уметь выводить и применять при решении задач формулы площади. Строить правильные многоугольники. |
|
|
| 81 | Длина окружности | 1 | Знать формулы длины окружности. Уметь решать задачи, применяя формулы длины окружности . |
|
|
| 82 | Длина окружности, число π; и длина дуги окружности. | 1 | Знать формулы длина окружности, число π; и длина дуги окружности; уметь применять на практике теорему об окружности, описанной около правильного многоугольника и окружности, вписанной в правильный многоугольник. |
|
|
| 83 | Площадь круга. Площадь кругового сектора. | 1 | Знать формулы площади круга и кругового сектора. Уметь решать задачи, применяя формулы для вычисления, длины окружности и дуги окружности, формулы площади круга и кругового сектора. |
|
|
| 84 | Площадь круга. Площадь кругового сектора. | 1 | Знать формулы площади круга и кругового сектора. Уметь решать задачи, применяя формулы для вычисления, длины окружности и дуги окружности, формулы площади круга и кругового сектора. |
|
|
| 85 | Площадь круга. Площадь кругового сектора. | 1 | Знать формулы площади круга и кругового сектора. Уметь решать задачи, применяя формулы для вычисления, длины окружности и дуги окружности, формулы площади круга и кругового сектора. |
|
|
| 86 | Длина окружности. Площадь круга | 1 | Знать формулы площади круга и кругового сектора. Уметь решать задачи, применяя формулы для вычисления, длины окружности и дуги окружности, формулы площади круга и кругового сектора. |
|
|
| 87 | Контрольная работа №4 по теме: “Длина окружности и площадь круга” | 1 | Уметь самостоятельно применять полученные теоретические знания на практике |
|
|
Степенные функции с натуральным показателем, их графики(10 уроков ).
| 88 | Степенные функции с натуральным показателем, их графики | 1 | Уметь анализировать ошибки, допущенные в контрольной работе, знать правильное решение заданийЗнать понятие степенной функции с натуральным показателем, о свойствах и графике функции. Уметь определять графики функций с четным и нечетным показателем, оформлять решения или сокращать решения, в зависимости от ситуации. |
|
|
| 89 | Степенные функции с натуральным показателем, их графики | 1 | Знать понятие степенной функции с натуральным показателем, о свойствах и графике функции. Уметь определять графики функций с четным и нечетным показателем, оформлять решения или сокращать решения,. |
|
|
| 90 | Степенные функции с натуральным показателем, их графики | 1 | Знать понятие степенной функции с натуральным показателем, о свойствах и графике функции. Уметь определять графики функций с четным и нечетным показателем, оформлять решения или сокращать решения, в зависимости от ситуации. |
|
|
| 91 | Степенные функции с натуральным показателем, их графики. Функции y = x–n (nN), их свойства и графики | 1 | Знать понятие степенной функции с натуральным показателем, о свойствах и графике функции. Уметь строить графики функций у=хn, у=х-n, рассматривать их свойства. |
|
|
| 92 | Степенные функции с натуральным показателем, их графики. Функции y = x–n (nN), их свойства и графики | 1 | Знать понятие степенной функции с натуральным показателем, о свойствах и графике функции. Уметь строить графики функций у=хn, у=х-n, рассматривать их свойства. |
|
|
| 93 | Использование графиков функций для решения уравнений, неравенств и систем | 1 | Знать о понятии степенной функции с отрицательным целым показателем, о свойствах и графике функции. Уметь оформлять решения уравнений, неравенств и систем, выполнять задания по заданному алгоритму, участие в диалоге. |
|
|
| 94 | Использование графиков функции для решения уравнений, неравенств и систем | 1 | Знать о понятии степенной функции с отрицательным целым показателем, о свойствах и графике функции. Уметь оформлять решения уравнений, неравенств и систем, выполнять задания по заданному алгоритму, участие в диалоге. |
|
|
| 95 | График функции: корень кубический; свойства. Примеры графических зависимостей, отражающих реальные процессы: колебание, показательный рост. Числовые функции, описывающие эти процессы. | 1 | Знать о понятии график функции: корень кубический; свойства; примеры графических зависимостей, отражающих реальные процессы: колебание, показательный рост; числовые функции, описывающие эти процессы. Уметь строить графики степенных функций с любым показателем степени; читать свойства по графику функции; строить графики функций по описанным свойствам |
|
|
| 96 | Параллельный перенос графиков функций вдоль осей координат и симметрия относительно осей. | 1 | Иметь представление о параллельный перенос графиков функций вдоль осей координат и симметрия относительно осей. Уметь оформлять решения, выполнять задания по заданному алгоритму, строить графики функций по описанным свойствам. |
|
|
| 97 | Контрольная работа №6по теме «Степенные функции с натуральным показателем, их графики» | 1 | Уметь самостоятельно применять полученные теоретические знания на практике |
|
|
Числовые последовательности( 16 уроков )
| 98 | Понятие последовательности. Числовые последовательности Способы задания | 1 | Уметь анализировать ошибки, допущенные в контрольной работе, знать правильное решение заданий. Знать определение числовой последовательности. Уметь задавать числовую последовательность аналитически, словесно, рекуррентно; привести примеры числовых последовательностей; определять понятия, приводить доказательства; объяснить изученные положения на самостоятельно подобранных конкретных примерах. |
|
|
| 99 | Понятие последовательности. Ограниченность и монотонность последовательности. | 1 | Знать понятия: числовая последовательность, n-й член последовательности, ограниченность и монотонность последовательности. Уметь задавать числовую последовательность, находить n-й член. |
|
|
| 100 | Понятие последовательности Числовые последовательности | 1 | Иметь представление о способах задания числовой последовательности. Знать определение числовой последовательности. Уметь задавать числовую последовательность аналитически, словесно, рекуррентно; привести примеры числовых последовательностей. |
|
|
| 101 | Арифметическая прогрессия. Формула общего члена арифметической прогрессии, формула суммы первых нескольких членов арифметической прогрессии. | 1 | Иметь представление о правиле задания арифметической прогрессии, формуле n-го члена арифметической прогрессии, формуле суммы членов конечной арифметической прогрессии. Знать правило и формулу n-го члена арифметической прогрессии, формулу суммы членов конечной арифметической прогрессии. Уметь применять формулы при решении задач. |
|
|
| 102 | Арифметическая прогрессия. Формула общего члена арифметической прогрессии, формула суммы первых нескольких членов арифметической прогрессии. | 1 | Знать правило и формулу n-го члена арифметической прогрессии, формулу суммы членов конечной арифметической прогрессии; Уметь применять формулы при решении задач. |
|
|
| 103 | Арифметическая прогрессия. Формула общего члена арифметической прогрессии, формула суммы первых нескольких членов арифметической прогрессии. | 1 | Иметь представление о правиле задания арифметической прогрессии, формуле n-го члена арифметической прогрессии, формуле суммы членов конечной арифметической прогрессии. Знать правило и формулу n-го члена арифметической прогрессии, формулу суммы членов конечной арифметической прогрессии; Уметь применять формулы при решении задач. |
|
|
| 104 | Арифметическая прогрессия. Характеристическое свойство. | 1 | Знать правило и формулу n-го члена арифметической прогрессии, формулу суммы членов конечной арифметической прогрессии; характеристическое свойство арифметической прогрессии и применение его при решении математических задач. Уметь применять формулы при решении задач; обосновывать суждения.
|
|
|
| 105
| Арифметическая прогрессия. Характеристическое свойство | 1 | Знать правило и формулу n-го члена арифметической прогрессии, формулу суммы членов конечной арифметической прогрессии; характеристическое свойство арифметической прогрессии и применение его при решении математических задач. Уметь применять формулы при решении задач; обосновывать суждения. |
|
|
| 106 | Геометрическая прогрессия Формулы общего члена геометрической прогрессии, суммы нескольких членов геометрической прогрессии | 1 | Знать правило и формулу n-го члена геометрической прогрессии, формулу суммы членов конечной геометрической прогрессии. Уметь применять формулы при решении задач; объяснить изученные положения на самостоятельно подобранных конкретных примерах. |
|
|
| 107 | Геометрическая прогрессия Формулы общего члена геометрической прогрессии, суммы нескольких членов геометрической прогрессии | 1 | Знать правило и формулу n-го члена геометрической прогрессии, формулу суммы членов конечной геометрической прогрессии. Уметь применять формулы при решении задач; объяснить изученные положения на самостоятельно подобранных конкретных примерах. |
|
|
| 108 | Геометрическая прогрессия Формулы общего члена геометрической прогрессии, суммы нескольких членов геометрической прогрессии | 1 | Знать правило и формулу n-го члена геометрической прогрессии, формулу суммы членов конечной геометрической прогрессии. Уметь применять формулы при решении задач; объяснить изученные положения на самостоятельно подобранных конкретных примерах |
|
|
| 109 | Геометрическая прогрессия. Бесконечно убывающая геометрическая прогрессия. Представление бесконечной периодической дроби в виде обыкновенной. | 1 | Знать бесконечно убывающая геометрическая прогрессии, представление бесконечной периодической дроби в виде обыкновенной. Уметь применять формулы при решении задач, объяснить изученные положения на самостоятельно подобранных конкретных примерах. |
|
|
| 110 | Геометрическая прогрессия. Характеристическое свойство. | 1 | Знать правило и формулу n-го члена геометрической прогрессии, формулу суммы членов конечной геометрической прогрессии; характеристическое свойство геометрической прогрессии и применение его при решении математических задач. Уметь применять формулы при решении задач; объяснить изученные положения на самостоятельно подобранных конкретных примерах. |
|
|
| 111 | Геометрическая прогрессия. Характеристическое свойство.
| 1 | Знать правило и формулу n-го члена геометрической прогрессии, формулу суммы членов конечной геометрической прогрессии; характеристическое свойство геометрической прогрессии и применение его при решении математических задач. Уметь применять формулы при решении задач; объяснить изученные положения на самостоятельно подобранных конкретных примерах. |
|
|
| 112 | Геометрическая прогрессия. Сложные Примеры движений фигур. Понятие движения. проценты. | 1 | Знать правило и формулу n-го члена геометрической прогрессии, формулу суммы членов конечной геометрической прогрессии; сложные проценты и применение его при решении математических задач. Уметь применять формулы при решении задач; объяснить изученные положения на самостоятельно подобранных конкретных примерах. |
|
|
| 113 | Контрольная работа №9 по теме «Числовые последовательности» | 1 | Уметь самостоятельно применять полученные теоретические знания на практике |
|
|
Геометрические преобразования (9 уроков)
| 114 |
Примеры движений фигур. Понятие движения.
| 1 | Уметь анализировать ошибки, допущенные в контрольной работе, знать правильное решение заданий.Знать, уметь применять свойства движений на практике.Уметь решать задачи с применением движений. |
|
|
| 115 | Симметрия фигур | 1 | Знать, уметь применять свойства движений на практике; доказывать, что симметрия являются движениями. Уметь решать задачи с применением движений. |
|
|
| 116 | Осевая симметрия и параллельный перенос | 1 | Знатьпонятие движения, виды движения: параллельный перенос. осевая симметрия. Уметь строить фигуры, полученные из данных параллельным переносом и поворотом вокруг точки. |
|
|
| 117 | Параллельный перенос. | 1 | Знать понятие движения, виды движения: параллельный перенос. Уметь строить фигуры, полученные из данных параллельным переносом и поворотом вокруг точки. |
|
|
| 118 | Поворот и центральная симметрия. | 1 | Знать понятие движения, виды движения: параллельный перенос, поворот. Уметь строить фигуры, полученные из данных параллельным переносом и поворотом вокруг точки. |
|
|
| 119 | Параллельный перенос. Поворот | 1 | Знать понятие движения, виды движения: параллельный перенос, поворот. Уметь строить фигуры, полученные из данных параллельным переносом и поворотом вокруг точки. |
|
|
| 120 | Симметрия фигур. Параллельный пере-нос. Поворот | 1 | Знать понятие движения, виды движения: параллельный перенос, поворот. Уметь строить фигуры, полученные из данных параллельным переносом и поворотом вокруг точки. |
|
|
| 121 | Понятие о гомотетии | 1 | Знать понятие движения, виды движения: параллельный перенос, поворот.гомотетия Уметь строить фигуры, полученные из данных параллельным переносом и поворотом вокруг точки. |
|
|
| 122 | Контрольная работа №5 “”Геометрические преобразования | 1 | Уметь самостоятельно применять полученные теоретические знания на практике |
|
|
Об аксиомах планиметрии (2 урока)
| 123,124 | Об аксиомах планиметрии (2 урока) | 2 | Уметь анализировать ошибки, допущенные в контрольной работе, знать правильное решение заданий.Знать об аксиомах планиметрии |
|
|
Элементы логики, комбинаторики, статистики и теории вероятностей( 12 уроков )
| 125 | Примеры решения комбинаторных задач.Перебор вариантов | 1 | Знать теорию множеств, методы решения комбинаторных задач. Уметь решать простейшие комбинаторные задачи,применять методы статистической обработки данные при решении задач. |
|
|
| 126 | Примеры решения комбинаторных задач. Правило умножения | 1 | Знать, как решать простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения. Уметь решать простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения. |
|
|
| 127 | Примеры решения комбинаторных задач. Правило умножения | 1 | Знать, как решать простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения. Уметь решать простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения. |
|
|
| 128 | Представление данных в виде диаграмм, таблиц | 1 | Знать теорию множеств, методы решения комбинаторных задач, формулу для подсчёта вероятности, виды случайных событий, методы обработки. Уметь решать простейшие комбинаторные задачи, простейшие вероятностные задачи, применять методы статистической обработки данных при решении задач. |
|
|
| 129 | Представление данных в виде графиков | 1 | Знать теорию множеств, методы решения комбинаторных задач, формулу для подсчёта вероятности, виды случайных событий, методы обработки. Уметь решать простейшие комбинаторные задачи, простейшие вероятностные задачи, применять методы статистической обработки данных при решении задач. |
|
|
| 130 | Понятие о статистическом выводе на основе выборки. Средние результаты измерений. | 1 | Знать и понимать статистические данные; понятие о статистическом выводе на основе выборки; что такое абсолютные, относительные и накопленные частоты. Уметь восстанавливать по одному виду частот другие; вычислять средние по таблице частот; вычислять характеристики разброса по таблице частот. |
|
|
| 131 | Контрольная работа № 11 по теме «Элементы логики, комбинаторики, статистики и теории вероятностей» | 1 | Уметь самостоятельно применять полученные теоретические знания на практике. |
|
|
| 132 | Частота события. Вероятность. Понятие и примеры случайных событий | 1 | Знать о событиях достоверных, невозможных, случайных; о классической вероятностной схеме, классическим определением вероятности. Уметь пользоваться формулой вычисления вероятности, решать задачи на характеристику событий. |
|
|
| 133 | Равновозможные события и подсчёт их вероятности | 1 | Знать методы решения комбинаторных задач, формулу для подсчёта вероятности, виды равновозможных событий, методы обработки. Уметь решать простейшие комбинаторные задачи, простейшие вероятностные задачи, применять методы статистической обработки данных при решении задач. |
|
|
| 134 | Равновозможные события и подсчёт их вероятности | 1 | Знать методы решения комбинаторных задач, формулу для подсчёта вероятности, виды равновозможных событий, методы обработки. Уметь решать простейшие комбинаторные задачи, простейшие вероятностные задачи, применять методы статистической обработки данных при решении задач. |
|
|
| 135 | Представление о геометрической вероятности | 1 | Знать правило геометрической вероятности. Уметь использовать технологии для создания базы данных. |
|
|
| 136 | Контрольная работа № 12 по теме «Элементы статистики и теории вероятностей» | 1 | Уметь самостоятельно применять полученные теоретические знания на практике. |
|
|
Наглядные представления о пространственных телах( 6часов)
| 137 | Правильные многогранники | 1 | Знать понятие правильного многогранника, элементов многогранника. Уметь различать виды многогранников, выполнять чертеж по условию задачи и решать задачи. |
|
|
| 138 | Наглядные представления о пространственных телах: куб, параллелепипед, призма, пирамида. | 1 | Иметь представление о пространственных телах: куб, параллелепипед, призма, пирамида. Уметь выполнять построение куба, параллелепипеда, призмы, пирамиды. |
|
|
| 139 | Наглядные представления о и пространственных телах: шар, цилиндр, конус | 1 | Знать определение шара, цилиндра, конуса. Уметь находить элементы конуса, шара и цилиндра. |
|
|
| 140 | Примеры сечений | 1 | Знать примеры сечений. Уметь выполнять чертежи по условию задачи. |
|
|
| 141 | Объём тела. Формулы объёма прямоугольного параллелепипеда, куба | 1 | Знать понятие объема, свойства объемов прямоугольного параллелепипеда и куба. Уметь решать задачи по теме. |
|
|
| 142 | Формулы объёма шара, цилиндра, конуса. Аксиомы планиметрии | 1 | Знать формулы объема шара, цилиндра, конуса. Уметь находить элементы цилиндра, конуса и шара. |
|
|
Повторение учебного материала 9 класса (28 часов)
| 143 | Неравенства и их системы | 1 | Знать понятие линейного и квадратного неравенств, алгоритмы их решения, знака объединения множеств. Уметь решать рациональные неравенства и системы рациональных неравенств; приводить примеры, |
|
|
| 144 | Система уравнений решение системы | 1 | Знать алгоритмы решения систем уравнений. Уметь решать нелинейные системы уравнений двух переменных различными методами; объяснить изученные положения на самостоятельно подобранных конкретных примерах. |
|
|
| 145 | Графическая интерпретация уравнений с двумя переменными и их систем с двумя переменными и их систем | 1 | Знать понятие графической интерпретации уравнений с двумя переменными и их систем. Уметь решать графически системы уравнений. |
|
|
| 146 | Использование графиков функций для решения уравнений и систем | 1 | Знать алгоритм графического способа решения системы уравнений. Уметь использовать графики при решении системы уравнений. |
|
|
| 147 | Числовые функции | 1 | Знать определение числовой функции. Уметь строить и описывать свойства элементарных функций; определять понятия, приводить доказательства; найти и устранить причины возникших трудностей. |
|
|
| 148
| Числовые последовательности | 1 | Знать определение числовой последовательности. Уметь задавать числовую последовательность аналитически, словесно, рекуррентно; привести примеры числовых последовательностей; определять понятия, приводить доказательства; объяснить изученные положения на самостоятельно подобранных конкретных примерах. |
|
|
| 149 | Примеры решения уравнений высших степеней | 1 | Знать алгоритм решения уравнений высшей степени. Уметь решать уравнения высших степеней используя различные приемы. |
|
|
| 150 | Примеры решения нелинейных систем | 1 | Знать алгоритмы решения нелинейных систем уравнений. Уметь при решении систем уравнений применять и использовать метод замены, метод алгебраического сложения и метод введения новой переменной. |
|
|
| 151 | Решение текстовых задач алгебраическим способом | 1 | Знать, как составлять математические модели реальных ситуаций и работать с составленной моделью. Уметь составлять математические модели реальных ситуаций и работать с составленной моделью; приводить примеры, подбирать аргументы, формулировать выводы; воспроизводить прочитанную информацию с заданной степенью свернутости; аргументировано отвечать на поставленные вопросы, осмыслить ошибки и устранить их. |
|
|
| 152 | Решение текстовых задач алгебраическим способом | 1 | Знать, как составлять математические модели реальных ситуаций и работать с составленной моделью. Уметь составлять математические модели реальных ситуаций и работать с составленной моделью; приводить примеры, подбирать аргументы, формулировать выводы; воспроизводить прочитанную информацию с заданной степенью свернутости; аргументировано отвечать на поставленные вопросы, осмыслить ошибки и устранить их. |
|
|
| 153 | Итоговая контрольная работа по алгебре | 1 | Уметь применять изученный теоретический материал при выполнении письменной работы. |
|
|
| 154 | Треугольник | 1 | Уметь анализировать ошибки, допущенные в контрольной работе, знать правильное решение заданий .Знать основные формулы треугольников. Уметь решать задачи, строить углы, вычислять координаты точки с помощью синуса, косинуса и тангенса угла, вычислять площадь треугольника по двум сторонам и углу между ними, решать треугольники. |
|
|
| 155 | Четырехугольник | 1 | Знать и понимать: понятия параллелограмм, трапеция, ромб, квадрат. Уметь выполнять задачи из разделов курса VIII класса, используя теорию: свойства, признаки параллелограмма, ромба, прямоугольника. |
|
|
| 156
| Многоугольники | 1 | Знать определение и свойства многоугольника. Уметь строить многоугольники, решать задачи |
|
|
| 157 | Измерение геометрических величин | 1 | Знать и понимать понятие длины, величины углов, площадей и объемов фигур. Уметь решать практические задачи, связанных с нахождением геометрических величин. |
|
|
| 158 | Векторы и координаты | 1 | Знать понятие координат вектора, находить координаты вектора, выполнять действия над векторами, заданными координатами. Уметь решать задачи на применение законов сложения, вычитания векторов, умножения вектора на число. |
|
|
| 159
| Понятие об аксиоматике и аксиоматическом построении геометрии. Пятый постулат Эвклида и его история | 1 | Знать определения, доказательства, аксиомы и теоремы, историю постулата Эвклида. Уметь практические задачи. |
|
|
| 160 | Геометрические преобразования | 1 | Знать названия геометрических фигур, свойства геометрических фигур, названия преобразований фигур. Уметь строить простейшие геометрические фигуры, различать их, находить общие черты, обобщать, делать выводы из собственных наблюдений, распознавать преобразования фигур, выполнять их, представлять себе форму фигуры по развертке и уметь складывать ее. |
|
|
| 161 | Итоговая контрольная работа по геометрии | 1 | Знать изученный материал. Уметь самостоятельно применять полученные теоретические знания на практике. |
|
|
| 162 | Множества и комбинаторика | 1 | Знать, как решать простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения. Уметь решать простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения; составлять план выполнения построений, приводить примеры, формулировать выводы. |
|
|
| 163 | Статистические данные | 1 | Знать понятие варианта, многоугольника распределения данных, кривой нормального распределения. Уметь обрабатывать статистические данные. |
|
|
| 164 | Вероятность | 1 | Знать, как решать простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения. Уметь пользоваться формулой вычисления вероятности, решать задачи на характеристику событий. |
|
|
| 165 | Доказательство | 1 | Знать формулировки и доказательства. Уметь проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования. |
|
|
| 166 | Способы задания функций и их свойства | 1 | Знать о способах задания функции: аналитическом, графическом, табличном, словесном. Уметь самостоятельно находить область определения функции, пользоваться навыками нахождения области определения функции, решая задания повышенной сложности. |
|
|
| 167 | Арифметическая прогрессия. Геометрическая прогрессия. | 1 | Знать правило и формулу n-го члена арифметической и геометрической прогрессии, формулу суммы членов конечной арифметической и геометрической прогрессии; характеристическое свойство арифметической и геометрической прогрессии и применение его при решении математических задач. Уметь решать задания на применение свойств арифметической и геометрической прогрессии; извлекать необходимую информацию из учебно-научных текстов; отделить основную информацию от второстепенной. |
|
|
| 168 169 | Итоговая контрольная работа | 2 | Знать изученный материал. Уметь самостоятельно применять полученные теоретические знания на практике. |
|
|
| 170 | Элементы логики, комбинаторики, статистике и теории вероятностей | 1 | Знать теорию множеств, методы решения комбинаторных задач, формулу для подсчёта вероятности, виды случайных событий, методы обработки. Уметь решать простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения ; составлять план выполнения построений, приводить примеры, формулировать выводы |
|
|
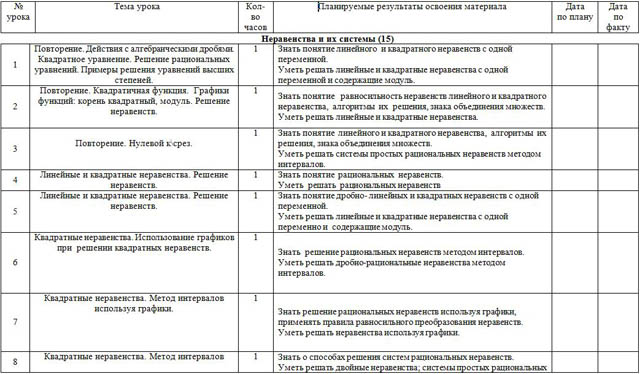

 Получите свидетельство
Получите свидетельство Вход
Вход


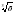 ее свойства и график. Использование графиков функций для решения уравнений, неравенств и систем. Примеры графических зависимостей, отражающих реальные процессы: колебание, показательный рост. Числовые функции, описывающие эти процессы. Параллельный перенос графиков функций вдоль осей координат и симметрия относительно осей.
ее свойства и график. Использование графиков функций для решения уравнений, неравенств и систем. Примеры графических зависимостей, отражающих реальные процессы: колебание, показательный рост. Числовые функции, описывающие эти процессы. Параллельный перенос графиков функций вдоль осей координат и симметрия относительно осей.








 Рабочая программа по математике (для 9-х классов) (0.12 MB)
Рабочая программа по математике (для 9-х классов) (0.12 MB)
 0
0 738
738 17
17 Нравится
0
Нравится
0



