СОДЕРЖАНИЕ
| 1. Пояснительная записка. | стр. 3 |
| 1.1. Общие цели образования с учетом специфики учебного предмета. | стр. 3 |
| 1.2. Нормативно-правовая база. | стр. 4 |
| 2. Общая характеристика учебного предмета | стр. 5 |
| 3. Описание места учебного предмета в учебном плане. | стр. 6 |
| 4. Личностные, метапредметные и предметные результаты освоения учебного предмета | стр. 7 |
| 5. Содержание учебного предмета. | стр. 9 |
| 5.1. Ценностные ориентиры содержания учебного предмета. | стр. 9 |
| 5.2. Перечень основных разделов, тем и последовательность их изучения, количество часов на изучение каждого раздела. | стр. 14 |
| 5.3. Характеристика основных содержательных линий. | стр. 16 |
| 5.4. Система оценки планируемых результатов, выраженная в формах и видах контроля. | стр. 17 |
| 6. Описание учебно-методического и материально-технического обеспечения образовательного процесса. | стр. 21 |
| 6.1. Учебно-методический комплекс. | стр. 21 |
| 6.2. Технические средства обучения, учебно-наглядные пособия, учебно-практическое и учебно-лабораторное оборудование, оборудование класса. | стр. 21 |
| 7. Планируемые результаты изучения учебного предмета. | стр. 23 |
ПРИЛОЖЕНИЕ 1 Календарно-тематическое планирование для 5 класса
ПРИЛОЖЕНИЕ 2 Календарно-тематическое планирование для 6 класса
- Пояснительная записка
Рабочая программа составлена основе федерального образовательного стандарта нового поколения, Примерной программы по учебным предметам «Стандарты второго поколения. Математика 5 – 9 класс» – М.: Просвещение, 2011 г. и «Математика. Сборник рабочих программ 5 – 6 классы», - М.Просвещение, 2011. Составитель Т. А. Бурмистрова.
Рабочая программа опирается на УМК:
- Учебник для учащихся 5 класса общеобразовательных учреждений под редакцией коллектива авторов: Н.Я. Виленкин, В.И. Жохов, А.С.Чесноков, С.И. Шварцбурд "Математика 5", издательство "Мнемозина", г.Москва, 2012г;
- Дидактические материалы Чесноков А.С., Нешков К. И. 2008.
При составлении рабочей программы учтены основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования.
Общие цели образования с учетом специфики учебного предмета.
Цели:
формирование представлений о математике как универсальном языке;
развитие логического мышления, пространственного воображения, алгоритмической культуры;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни и для изучения школьных естественных дисциплин на базовом уровне;
воспитание средствами математики культуры личности;
понимание значимости математики для научно-технического прогресса;
отношение к математике как к части общечеловеческой культуры через знакомство с историей её развития.
Задачи:
сохранить теоретические и методические подходы, оправдавшие себя в практике преподавания в начальной школе;
предусмотреть возможность компенсации пробелов в подготовке школьников и недостатков в их математическом развитии, развитии внимания и памяти;
обеспечить уровневую дифференциацию в ходе обучения;
обеспечить базу математических знаний, достаточную для изучения алгебры и геометрии, а также для продолжения образования;
сформировать устойчивый интерес учащихся к предмету;
выявить и развить математические и творческие способности;
развивать навыки вычислений с натуральными числами;
учить выполнять сложение и вычитание обыкновенных дробей с одинаковыми знаменателями, действия с десятичными дробями;
дать начальные представления об использование букв для записи выражений и свойств;
учить составлять по условию текстовой задачи, несложные линейные уравнения;
продолжить знакомство с геометрическими понятиями;
развивать навыки построения геометрических фигур и измерения геометрических величин.
Нормативно правовая база
Рабочая программа учебного предмета «Математика – 5, 6» (далее Рабочая программа) составлена на основании следующих нормативно-правовых документов:
Федерального компонента государственного стандарта основного общего образования по математике, утвержденного приказом Минобразования России от 5.03.2004 г. № 1089. Стандарт опубликован в издании "Федеральный компонент государственного стандарта общего образования. Часть I. Начальное общее образование. Основное общее образование" (Москва, Министерство образования Российской Федерации, 2004)
Закона Российской Федерации «Об образовании» (статья 7, 9, 32).
Примерной и авторской программы основного общего образования по математике (Программа. Планирование учебного материала. Математика. 5-6 классы / [авт.-сост. В.И. Жохов] – 2-е изд., стер. – М.: Мнемозина, 2010. – 31 с.).
Требования к результатам обучения, представленных в Стандарте основного общего образования;
Учебный план МБОУ «Средняя общеобразовательная школа №17» г. Заволжье Городецкого муниципального района на 2014-2015 учебный год;
Приказ от 31 марта 2014г. №253 «Об утверждении федерального перечня учебников, рекомендованных к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования»;
Положение о структуре, разработке и утверждении рабочих программ учебных курсов, предметов, дисциплин (модулей), иных компонентов в муниципальном бюджетном образовательном учреждении «Средняя общеобразовательная школа №17» г. Заволжье, реализующего образовательные программы начального общего, основного общего, среднего общего образования;
Программа соответствует учебнику «Математика» для шестого класса образовательных учреждений /Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбург – М. Мнемозина, 2014 гг./ и обеспечена учебно-методическим комплектом «Математика» для 6-го класса авторов Н.Я. Виленкин и др. (М.: Мнемозина).
Общая характеристика учебного предмета
Курс математики в 5-6 классах, с одной стороны, является непосредственным продолжением курса математики начальной школы, систематизирует, обобщает и развивает полученные там знания, с другой стороны, позволяет учащимся адаптироваться к новому уровню изучения предмета, создает необходимую основу, на которой будут базироваться систематические курсы 7-9 классов.
Практическая значимость школьного курса математики 5—6 классов обусловлена тем, что её объектом являются количественные отношения действительного мира. Математическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С её помощью моделируются и изучаются явления и процессы, происходящие в природе.
Математика является одним из опорных предметов основной школы. Овладение учащимися системой математических знаний и умений необходимо в повседневной жизни, для изучения смежных дисциплин и продолжения образования. В первую очередь это относится к предметам естественнонаучного цикла, в частности к физике. Развитие логического мышления учащихся при обучении математике в 5—6 классах способствует усвоению предметов гуманитарного цикла. Практические умения и навыки арифметического характера необходимы для трудовой и профессиональной подготовки школьников.
Развитие у учащихся правильных представлений о сущности и происхождении математических абстракций, о соотношении реального и идеального, о характере отражения математической наукой явлений и процессов реального мира, о месте математики в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся, а также формированию качеств мышления, необходимых для адаптации в современном информационном обществе.
Требуя от учащихся умственных и волевых усилий, концентрации внимания, активности воображения, математика развивает нравственные черты личности (настойчивость, целеустремленность, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления) и умение аргументировано отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения. Решение текстовых задач на всех этапах учебного процесса развивают творческие способности школьников.
Изучение математики в 5-6 классах позволяет формировать умения и навыки умственного труда: планирование своей работы, поиск рациональных путей её выполнения, критическую оценку результатов. В процессе изучения математики школьники учатся излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобретают навыки чёткого, аккуратного и грамотного выполнения математических записей.
Важнейшей задачей школьного курса математики является развитие логического мышления учащихся. Сами объекты математических умозаключений и правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить чёткие определения, развивают логическую интуицию, кратко и наглядно раскрывают механизм логических построений и учат их применению. Показывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, математика вносит значительный вклад в эстетическое воспитание учащихся.
Описание места учебного предмета в базисном плане
В соответствии с учебным планом основного общего образования в курсе математики выделяются два этапа — 5-6 классы и 7-9 классы, у каждого из которых свои самостоятельные функции. В 5-6 классах изучается интегрированный предмет «Математика», в 7-9 классах — два предмета «Алгебра» и «Геометрия».
Соответственно действующему в ОУ учебному плану рабочая программа предусматривает следующий вариант организации процесса обучения в 5-х классах: базовый уровень обучения в объеме 170 часов, в неделю – 5 часов, в 6-х классах: базовый уровень обучения в объеме 170 часов, в неделю – 5 часов.
Личностные, метапредметные и предметные результаты освоения содержания курса
Программа позволяет добиваться следующих результатов освоения образовательной программы основного общего образования:
личностные:
ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
формирования коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, учебно-исследовательской, творческой и других видах деятельности;
умения ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
первоначального представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичности мышления, умения распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативности мышления, инициативы, находчивости, активности при решении арифметических задач;
умения контролировать процесс и результат учебной математической деятельности;
формирования способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
способности самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умения осуществлять контроль по образцу и вносить необходимые коррективы;
способности адекватно оценивать правильность или Ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
умения устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;
умения создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
развития способности организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, взаимодействовать и находить общие способы работы; умения работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
формирования учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентностй);
первоначального представления об идеях и о методах математики как об универсальном языке науки и техники;
развития способности видеть математическую задачу в других дисциплинах, в окружающей жизни;
умения находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умения понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умения выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
понимания сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
умения самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
способности планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
предметные:
1) умения работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), развития способности обосновывать суждения, проводить классификацию;
владения базовым понятийным аппаратом: иметь представление о числе, дроби, процентах, об основных геометрических объектах (точка, прямая, ломаная, угол, многоугольник, многогранник, круг, окружность, шар, сфера и пр.), формирования представлений о статистических закономерностях в реальном мире и различных способах их изучения;
умения выполнять арифметические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;
умения пользоваться изученными математическими формулами,"
знания основных способов представления и анализа статистических данных; умения решать задачи с помощью перебора всех возможных вариантов;
умения применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
Содержание учебного предмета
Ценностные ориентиры содержания учебного предмета.
Содержание программы 5 класс
1. Натуральные числа и шкалы
Обозначение натуральных чисел. Отрезок, длина отрезка. Треугольник. Плоскость, прямая, луч. Шкалы и координаты. Меньше или больше.
Основная цель – систематизировать и обобщить сведения о натуральных числах, полученные в начальной школе; закрепить навыки построения и измерения отрезков
2.Сложение и вычитание натуральных чисел
Сложение натуральных чисел и его свойства. Вычитание. Решение текстовых задач. Числовые и буквенные выражения. Буквенная запись свойств сложения и вычитания. Уравнение.
Основная цель – закрепить и развить навыки сложения и вычитания натуральных чисел.
3. Умножение и деление натуральных чисел
Умножение натуральных чисел и его свойства. Деление. Деление с остатком. Упрощение выражений. Порядок выполнения действий. Степень числа. Квадрат и куб числа.
Основная цель – закрепить и развить навыки арифметических действий с натуральными числами
4. Площади и объемы
Формулы. Площадь. Формула площади прямоугольника. Единицы измерения площадей. Прямоугольный параллелепипед. Объемы. Объем прямоугольного параллелепипеда.
Основная цель – расширить представление учащихся об измерении геометрических величин на примере вычисления площадей и объемов, систематизировать известные им сведения об единице измерения.
5. Обыкновенные дроби
Окружность и круг. Доли. Обыкновенные дроби. Сравнение дробей. Правильные и неправильные дроби. Сложение и вычитание дробей с одинаковыми знаменателями .Деление и дроби. Смешанные числа. Сложение и вычитание смешанных чисел.
Основная цель – познакомить учащихся с понятием дроби в объеме, достаточном для введения десятичных дробей.
6. Десятичные дроби. Сложение и вычитание десятичных дробей
Десятичная запись дробных чисел. Сравнение десятичных дробей. Сложение и вычитание десятичных дробей. Приближённые значения чисел. Округление чисел.
Основная цель – выработать умение читать, записывать, сравнивать, округлять десятичные дроби, выполнять сложение и вычитание десятичных дробей.
7. Умножение и деление десятичных дробей
Умножение десятичных дробей на натуральные числа. Деление десятичных дробей на натуральные числа. Умножение десятичных дробей. Деление на десятичную дробь. Среднее арифметическое.
Основная цель – выработать умение умножать и делить десятичные дроби, выполнять задания на все действия с натуральными числами и десятичными дробями
8. Инструменты для вычислений и измерений
Микрокалькулятор. Проценты. Угол. Прямой и развернутый угол. Чертёжный треугольник. Измерение углов. Транспортир. Круговые диаграммы.
Основная цель – сформировать умения решать простейшие задачи на проценты, выполнять измерение и построение углов.
9. Повторение
Содержание программы 6 класс
1. Делимость чисел
Делители и кратные числа. Общий делитель и общее кратное. Признаки делимости на 2, 3, 5, 9, 10. Простые и составные числа. Разложение натурального числа на простые множители.
Основная цель — завершить изучение натуральных чисел, подготовить основу для освоения действий с обыкновенными дробями.
В данной теме завершается изучение вопросов, связанных с натуральными числами. Основное внимание должно быть уделено знакомству с понятиями «делитель» и «кратное», которые находят применение при сокращении обыкновенных дробей и при их приведении к общему знаменателю. Упражнения полезно выполнять с опорой на таблицу умножения — прямым подбором.
Определенное внимание уделяется знакомству с признаками делимости, понятиям простого и составного чисел. При их изучении целесообразно формировать умения проводить простейшие умозаключения, обосновывая свои действия ссылками на определение, правило.
Учащиеся должны уметь разложить число на множители. Например, они должны понимать, что 36 = 6· 6 = 4· 9 = 2 ·18 и т. п. Умения разложить число на простые множители не обязательно добиваться от всех учащихся.
2. Сложение и вычитание дробей с разными знаменателями
Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Понятие о наименьшем общем знаменателе нескольких дробей. Сравнение дробей. Сложение и вычитание дробей. Решение текстовых задач.
Основная цель — выработать прочные навыки преобразования дробей, сложения и вычитания дробей.
Одним из важнейших результатов обучения является усвоение основного свойства дроби, применяемого для преобразования дробей: сокращения, приведения к новому знаменателю. Умение приводить дроби к общему знаменателю используется для сравнения дробей.
При рассмотрении действий с дробями используются правила сложения и вычитания дробей с одинаковыми знаменателями, понятие смешанного числа. Важно обратить внимание на случай вычитания дроби из целого числа.
3. Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей. Основные задачи на дроби.
Основная цель — выработать прочные навыки арифметических действий с обыкновенными дробями и решения основных задач на дроби.
В этой теме завершается работа над формированием навыков арифметических действий с обыкновенными дробями. Навыки должны быть достаточно прочными, чтобы учащиеся не испытывали затруднений в вычислениях с рациональными числами, чтобы алгоритмы действий с обыкновенными дробями могли стать в дальнейшем опорой для формирования умений выполнять действия с алгебраическими дробями.
Расширение аппарата действий с дробями позволяет решать текстовые задачи, в которых требуется найти дробь от числа или число по данному значению его дроби.
4. Отношения и пропорции
Пропорция. Основное свойство пропорции. Решение задач с помощью пропорции. Понятия о прямой и обратной пропорциональности величин. Задачи на пропорции. Масштаб. Формулы длины окружности и площади круга. Шар.
Основная цель — сформировать понятия пропорции, прямой и обратной пропорциональности величин.
Необходимо, чтобы учащиеся усвоили основное свойство пропорции, так как оно находит применение на уроках математики, химии, физики. В частности, достаточное внимание должно быть уделено решению с помощью пропорции задач на проценты.
Понятия о прямой и обратной пропорциональности величин можно сформировать как обобщение нескольких конкретных примеров, подчеркнув при этом практическую значимость этих понятий, возможность их применения для упрощения решения соответствующих задач.
В данной теме даются представления о длине окружности и площади круга. Соответствующие формулы к обязательному материалу не относятся. Рассмотрение геометрических фигур завершается знакомством с шаром.
5. Положительные и отрицательные числа
Положительные и отрицательные числа. Противоположные числа. Модуль числа и его геометрический смысл. Сравнение чисел. Целые числа. Изображение чисел на координатной прямой. Координата точки.
Основная цель — расширить представления учащихся о числе путем введения отрицательных чисел.
Целесообразность введения отрицательных чисел показывается на содержательных примерах. Учащиеся должны научиться изображать положительные и отрицательные числа на координатной прямой. В дальнейшем она будет служить наглядной основой для правил сравнения чисел, сложения и вычитания чисел.
Специальное внимание должно быть уделено усвоению вводимого здесь понятия модуля числа, прочное знание которого необходимо для формирования умения сравнивать отрицательные числа, а в дальнейшем и для овладения алгоритмами арифметических действий с положительными и отрицательными числами.
6. Сложение и вычитание положительных и отрицательных чисел
Сложение и вычитание положительных и отрицательных чисел.
Основная цель — выработать прочные навыки сложения и вычитания положительных и отрицательных чисел.
Действия с отрицательными числами вводятся на основе представлений об изменении величин: сложение и вычитание чисел иллюстрируется соответствующими перемещениями точек координатной прямой. При изучении данной темы отрабатываются алгоритмы сложения и вычитания при выполнении действий с целыми и дробными числами.
7. Умножение и деление положительных и отрицательных чисел
Умножение и деление положительных и отрицательных чисел. Понятие о рациональном числе. десятичное приближение обыкновенной дроби. Применение законов арифметических действий для рационализации вычислений.
Основная цель — выработать прочные навыки арифметических действий с положительными и отрицательными числами.
Навыки умножения и деления положительных и отрицательных чисел отрабатываются сначала при выполнении отдельных действий, а затем в сочетании с навыками сложения и вычитания при вычислении значений числовых выражений.
При изучении данной темы учащиеся должны усвоить, что для обращения обыкновенной дроби в десятичную достаточно разделить (если это возможно) числитель на знаменатель. В каждом конкретном случае они должны знать, в какую дробь обращается данная обыкновенная дробь — в десятичную или периодическую. Учащиеся должны знать представление в виде десятичной дроби таких дробей, как 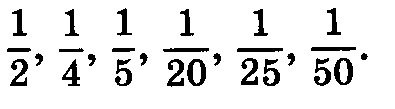
8. Решение уравнений
Простейшие преобразования выражений: раскрытие скобок, приведение подобных слагаемых. Решение линейных уравнений. Примеры решения текстовых задач с помощью линейных уравнений.
Основная цель — подготовить учащихся к выполнению преобразований выражений, решению уравнений.
Преобразования буквенных выражений путем раскрытия скобок и приведения подобных слагаемых отрабатываются в той степени, в которой они необходимы для решения несложных уравнений.
Введение арифметических действий над отрицательными числами позволяет ознакомить учащихся с общими приемами решения линейных уравнений с одной переменной.
9. Координаты на плоскости
Построение перпендикуляра к прямой и параллельных прямых с помощью чертежного треугольника и линейки. Прямоугольная система координат на плоскости, абсцисса и ордината точки. Примеры графиков, диаграмм.
Основная цель — познакомить учащихся с прямоугольной системой координат на плоскости.
Учащиеся должны научиться распознавать и изображать перпендикулярные и параллельные прямые. Основное внимание следует уделить отработке навыков их построения с помощью линейки и чертежного треугольника, не требуя воспроизведения точных определений.
Основным результатом знакомства учащихся с координатной плоскостью должны стать знания порядка записи координат точек плоскости и их названий, умения построить координатные оси, отметить точку по заданным координатам, определить координаты точки, отмеченной на координатной плоскости.
Формированию вычислительных и графических умений способствует построение столбчатых диаграмм. При выполнении соответствующих упражнений найдут применение изученные ранее сведения о масштабе и округлении чисел.
Повторение. Решение задач.
5.2. Перечень основных разделов, тем и последовательность их изучения, количество часов на изучение каждого раздела.
| № п/п | Разделы, темы 5 класс | Количество часов |
|
|
| 1 | Натуральные числа и шкалы. | 15 |
| 2 | Сложение и вычитание натуральных чисел. | 21 |
| 3 | Умножение и деление натуральных чисел. | 27 |
| 4 | Площади и объемы. | 12 |
| 5 | Обыкновенные дроби. | 23 |
| 6 | Десятичные дроби. Сложение и вычитание десятичных дробей. | 13 |
| 7 | Умножение и деление десятичных дробей. | 26 |
| 8 | Инструменты для вычислений и измерений. | 17 |
| 9 | Повторение курса математики 5-го класса | 16 |
| № п/п | Разделы, темы 6 класс | Количество часов
|
| 1 | Делимость чисел | 20 |
| 2 | Сложение и вычитание дробей с разными знаменателями | 22 |
| 3 | Умножение и деление обыкновенных дробей. | 31 |
| 4 | Отношения и пропорции | 19 |
| 5 | Положительные и отрицательные числа. | 13 |
| 6 | Сложение и вычитание положительных и отрицательных чисел | 11 |
| 7 | Умножение и деление положительных и отрицательных чисел. | 12 |
| 8 | Решение уравнений. | 13 |
| 9 | Координаты на плоскости | 13 |
| 10 | Повторение. Решение задач | 16 |
ПЕРЕЧЕНЬ ТЕМ КОНТРОЛЬНЫХ РАБОТ
5 класс
Шкалы и координаты
Сложение и вычитание натуральных чисел
Решение уравнений
Умножение и деление натуральных чисел
Упрощение выражений
Площади и объемы
Правильные и неправильные дроби
Сложение и вычитание дробей
Сложение и вычитание десятичных дробей
Умножение и деление десятичных дробей на натуральные числа
Умножение и деление десятичных дробей
Проценты
Измерение углов
Итоговая контрольная работа
6 класс
1. Делимость чисел
2. Сложение и вычитание дробей с разными знаменателями
3. Сложение и вычитание смешанных чисел
4. Умножение дробей
5. Деление дробей
6. Дробные выражения
7. Пропорции
8. Окружность и шар
9. Противоположные числа
10. Сложение и вычитание чисел с разными знаками
11. Умножение и деление чисел с разными знаками
12. Подобные слагаемые
13. Решение уравнений
14. Координаты на плоскости
15. Итоговая контрольная работа
5.3. Характеристика основных содержательных линий
В данном курсе представлены следующие содержательные линии: «Натуральные числа», «Дроби», «Рациональные числа», «Числовые выражения», «Текстовые задачи», «Измерения, приближения и оценки», «Элементы алгебры», «Координаты», «Начальные геометрические сведения»,
«Геометрические величины», «Множества» .
В рамках указанных содержательных линий решаются следующие задачи:
− развиваются представления о числе и роли вычислений в практической деятельности, развиваются практические навыки устных и письменных вычислений, формируется вычислительная культура;
−развиваются геометрические представления, изобразительные умения и глазомер;
−формируются навыки преобразований числовых и буквенных выражений;
−развивается логическое мышление и математическая речь;
Изучение математики в 5-6 классах направлено на достижение следующих целей:
−интеллектуальное развитие, которое заключается в формировании ясности, точности и логичности мышления, интуиции, алгоритмической культуры, геометрических представлений;
−формирование устойчивого интереса к изучению математики, создание фундамента для изучения в следующих классах систематических курсов алгебры и геометрии, а также школьных предметов естественнонаучного цикла;
−воспитание упорства, аккуратности, способностей к преодолению трудностей;
5.4. Система оценки планируемых результатов, выраженная в формах и видах контроля.
Единые нормы являются основой при оценке как контрольных, так и всех других письменных работ по математике. Применяя эти нормы, учитель должен индивидуально подходить к оценке каждой письменной работы учащегося, обращать внимание на качество выполнения работы в целом, а затем уже на количество ошибок и на их характер.
Оценка письменной работы определяется с учётом прежде всего её общего математического уровня, оригинальности, последовательности, логичности её выполнения, а также числа ошибок и недочётов и качества оформления работы.
Ошибка, повторяющаяся в одной работе несколько раз, рассматривается как одна ошибка.
За орфографические ошибки, допущенные учениками, оценка не снижается; об орфографических ошибках доводится до сведения преподавателя русского языка. Однако ошибки в написании математических терминов, уже встречавшихся школьникам класса, должны учитываться как недочёты в работе.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
1. Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Описание материально-технического обеспечения образовательного процесса
Учебно-методический комплекс
Примерной программы по учебным предметам «Стандарты второго поколения. Математика 5 – 9 класс» – М.: Просвещение, 2011 г.
2. «Математика. Сборник рабочих программ 5 – 6 классы», - М.Просвещение, 2011. Составитель Т. А. Бурмистрова.
Математика 5, 6. Учебник для общеобразовательных учреждений. Авторы: Н.Я. Виленкин, В.И. Жохов, А.С.Чесноков, С.И. Шварцбурд , издательство "Просвещение", г. Москва 2012
4. Дидактические материалы Чесноков А.С., Нешков К. И., издательство "Мнемозина", г. Москва 2008
20 тестов по математике 5-6 классы. С. С. Минаева , издательство «Экзамен» 2011
6. CD: «Математика 5 – 6 класс. Поурочные разработки»
6. 2. Технические средства обучения, учебно-наглядные пособия, учебно-дидактические материалы, оборудование класса.
| № п/п | Наименование раздела, наименование объектов и средств материально-технического обеспечения | Количество на 32 учащихся |
% обеспеченности |
|
|
| Базовый уровень |
|
|
| Иллюстрации (плакаты) |
|
|
| 1. | Комплект таблиц «Натуральные числа» | 1х10 | 100% |
|
| Средства ИКТ |
|
|
|
| Средства икт (цифровые образовательные ресурсы (цор)
|
|
|
| 2 | Операционная система Linux | 1 | 100% |
|
3 | Операционная система Windows XP | 1 | 100% |
|
| Цор ( инструменты общепедагогические)
| 1 | 100% |
| 4 | Microsoft Offis 2007 | 1 | 100% |
| 5 | Adobe Reader | 1 | 100% |
| 6 | KMPlayer | 1 | 100% |
|
| Цор (инструменты специализированные) |
|
|
| 7 | Диск «Математика. Справочник для школьника | 1 | 100% |
| 8 | Диск «Математика 5-6» | 1 | 100% |
|
| Информационные источники ( специализированные) |
|
|
| 9 | http://urokimatematiki.ru |
|
|
| 10 | http://intergu.ru/ |
|
|
| 11 | http://karmanform.ucoz.ru |
|
|
| 12 | http://polyakova.ucoz.ru/ |
|
|
| 13 | http://le-savchen.ucoz.ru/ |
|
|
| 14 | http://www.it-n.ru/ |
|
|
| 15 | http://www.openclass.ru/ |
|
|
|
| Учебно-лабораторное оборудование |
|
|
| 16 | Мультимедийный компьютер
| 1 | 100% |
| 17 | Мультимедиапроектор
| 1 | 100% |
| 18 | Интерактивная доска
| 1 | 100% |
| 19 | Аудиторная доска с магнитной поверхностью и набором приспособлений для крепления таблиц | 1 | 100% |
| 20 | Комплект инструментов классных: линейка, транспортир, угольник (300, 600), угольник (450, 450), циркуль | 1 | 100% |
Планируемые результаты изучения учебного предмета
Натуральные числа. Дроби. Рациональные числа
По завершении изучения курса математики 5-6 классов выпускник научится:
• понимать особенности десятичной системы счисления;
• оперировать понятиями, связанными с делимостью натуральных чисел;
• выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;
• сравнивать и упорядочивать рациональные числа;
• выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применение калькулятора;
• использовать понятия и умения, связанные с пропорциональностью величин, процентами, в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчёты.
Выпускник получит возможность:
• познакомиться с позиционными системами счисления с основаниями, отличными от 10;
• углубить и развить представления о натуральных числах и свойствах делимости;
• научиться использовать приёмы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.
Измерения, приближения, оценки
Выпускник научится:
• использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин.
Выпускник получит возможность:
• понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближённым.
Элементы алгебры
Выпускник научится:
• оперировать понятиями «числовое выражение», «буквенное выражение», упрощать выражения, содержащие слагаемые с одинаковым буквенным множителем; работать с формулами;
• решать простейшие линейные уравнений с одной переменной;
• понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
• понимать и применять терминологию и символику, связанную с отношением неравенства, в простейших случаях.
Выпускник получит возможность:
• научиться выполнять преобразования целых буквенных выражений, применяя законы арифметических действий;
• овладеть простейшими приёмами решения уравнений; применять аппарат уравнений для решения разнообразных текстовых (сюжетных) задач.
Описательная статистика и вероятность
Выпускник получит возможность научиться:
• находить вероятность случайного события в простейших случаях;
• решать простейшие комбинаторные задачи на нахождение числа объектов или их комбинаций с использованием правила произведения.
Наглядная геометрия
Выпускник научится:
• распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры;
• пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения;
• распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;
• находить значения длин линейных элементов фигур, градусную меру углов от 0° до 180°;
• распознавать развёртки куба, прямоугольного параллелепипеда;
• строить развёртки куба и прямоугольного параллелепипеда;
• определять по линейным размерам развёртки фигуры линейные размеры самой фигуры и наоборот;
• вычислять площадь прямоугольника, круга, прямоугольного треугольника и площади фигур, составленных из них, объём прямоугольного параллелепипеда.
Выпускник получит возможность:
• научиться вычислять объёмы пространственных геометрических фигур, составленных из прямоугольных параллелепипедов;
• углубить и развить представления о пространственных геометрических фигурах;
• научиться применять понятие развёртки для выполнения практических расчётов.
27

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике (5-6 классы) (0.18 MB)
Рабочая программа по математике (5-6 классы) (0.18 MB)
 0
0 2124
2124 219
219 Нравится
0
Нравится
0






