РАБОЧАЯ ПРОГРАММА
ПО МАТЕМАТИКЕ
8 КЛАСС
БАЗОВЫЙ УРОВЕНЬ
2013 — 2014 ученый год
Мордкович А.Г. Алгебра: Учебник для 8 кл. общеобразовательных учреждений /
Л.С. Атанасян Геометрия для 7-9 кл. общеобразовательных. Учреждений.
(2 часа алгебры и 1 час геометрии в неделю)
Составитель: Топкасова
Светлана Николаевна, учитель математики
2013 г.
СОДЕРЖАНИЕ
| № п/п |
| стр |
| 1 | Пояснительная записка | 3 |
| 2 | Требования к уровню подготовки | 5 |
| 3 | Учебно-тематический план
| 8 |
| 4 | Содержание тем учебной программы
| 9 |
| 5 | Контроль уровня обученности
| 16 |
| 6 | Перечень литературы и средств обучения
| 19 |
| 7 | Приложения
| 20 |
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа учебного предмета «математика» составлена в соответствии с требованиями федерального компонента государственного стандарта общего образования (Приказ МО РФ от 05.03.2004 №1089) и примерной программы по математике на основе Федерального компонента государственного стандарта основного общего образования Министерства образования и науки РФ и программы к УМК Мордковича А.Г. по алгебре 8 класс и УМК Атанасяна Л.С. по геометрии 8 класс.
Данный учебный предмет имеет своей целью:
• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Изучение предмета «математика» в 8 классе способствует решению следующих задач:
развитие вычислительной культуры, формирование навыков инструментальных вычислений;
овладение символическим языком алгебры;
использование функционально-графических представлений для описания и анализа реальных зависимостей;
формирование представлений о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развитие логического мышления: умение логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, проводить доказательства.
Данная программа содержит все темы, включенные в федеральный компонент содержания образования.
Рабочая программа составлена с учетом особенностей психофизического развития и возможностей обучающихся: на освоение программы отведено 102 часа, в соответствии с индивидуальной программой реабилитации ребенка-инвалида.
Программа «Математика» модульная (включает два модуля: «Алгебра» и «Геометрия»). Строение курса в форме параллельного изучения модулей «Алгебра» по 3 часа в неделю и «Геометрия » по 1часу в неделю.
Модуль «Алгебра» в рабочей программе 8 класса включает следующие содержательные компоненты по математике: «арифметика» (частично); «алгебра»; «элементы логики, комбинаторики, статистики и теории вероятностей» (частично).
Обучение ведется по учебно-методическому комплекту А.Г.Мордковича., который состоит из учебника «Алгебра. 8 класс», методических рекомендаций к нему, дидактических материалов.
Содержание учебника и программы соответствует федеральному компоненту государственного стандарта общего образования и учитывает федеральный базисные учебный план.
Некоторые математические вопросы, полезные для создания целостного представления о предмете, но не находящие достаточного применения в других разделах данного курса, изучаются в ознакомительном плане и не являются объектом итогового контроля знаний выпускников школы. В программе эти вопросы выделены курсивом или подчеркнуты.
В разделах «Содержание тем учебного курса» и «Учебно-тематический план» материал расположен в соответствии с главами учебников.
В программу курса включены вопросы, позволяющие заложить прочный фундамент как для продолжения в 9, 10—11 классах изучения математики и предметов естественнонаучного цикла в любом из профилей, так и для применения математического аппарата в практической деятельности.
Модуль «Геометрия» в 8 классе, соответственно, включает следующие содержательные компоненты по математике: «геометрия»; «элементы логики, комбинаторики, статистики и теории вероятностей» (частично). Обучение ведется по учебнику Л.С. Атанасян для 7 – 9 – х классов.,2011г.
Курсивом выделен материал, который подлежит изучению, но не включается в требования к уровню подготовки обучающихся, подчёркнутые темы являются расширением стандарта посредством данных УМК.
Учебный процесс организован дистанционно с каждым обучающимся отдельно посредством сети Интернет с использованием ipтехнологии (Skype).Формами организации учебного процесса являются дистанционные уроки, конференции, беседы, консультации, дистанционные курсы.
Вводный, текущий, итоговый контроль проводится в форме контрольной работы и тестов Материалы контроля представлены в приложении.
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ
В результате изучения данного предмета в 8 классе обучающийся должен
знать:
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели к необходимости расширения понятия числа;
каким образом геометрия возникла из практических задач землемерия;
существо понятия алгоритма; примеры алгоритмов;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
смысл идеализации, позволяющий решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь:
■ по арифметике
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначными знаменателем и числителем;
устно оценивать результаты вычислений; осуществлять проверку результата вычисления с использованием различных приемов;
переходить от одной формы записи чисел к другой: представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную дробь в виде десятичной, проценты в виде дроби и дробь в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа, находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать крупные единицы через мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
■ по алгебре
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления; осуществлять подстановку одного выражения в другое; выражать из формул одну из переменных;
выполнять основные действия со степенями с целыми показателями, с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений;
решать линейные и квадратные неравенства с одной переменной.
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств; описывать свойства изученных функций, строить их графики;
■ по геометрии
пользоваться языком геометрии для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач;
вычислять значения геометрических величин (длин, углов, площадей) в том числе: находить стороны, углы и площади треугольников, длины ломаных, площадей основных геометрических фигур;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
■ по элементам логики, комбинаторике, статистике и теории вероятностей
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках;
составлять таблицы, строить диаграммы и графики;
вычислять средние значения результатов измерений;
решать комбинаторные задачи путём систематического перебора возможных вариантов, а так же с использованием правила произведения;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности событий в простейших случаях.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
■ по арифметике
решения несложных практических расчетных задач, в том числе с использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретировать результаты решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
■ по алгебре
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретаций графиков реальных зависимостей между величинами;
■ по геометрии
описания реальных ситуаций на языке геометрии;
решение геометрических задач с использованием тригонометрии.
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построения геометрическими инструментами (линейка, угольник, циркуль, транспортир);
■ по элементам логики, комбинаторике, статистике и теории вероятностей
выстраивания аргументации при доказательстве (в форме монолога и диалога);
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости.
УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН
МОДУЛЬ «АЛГЕБРА»
| № п\п | Тема | Количество часов | В том числе |
| Самостоятельные работы | Контрольные работы |
| 1 | Алгебраические дроби. Арифметические операции над алгебраическими дробями | 14 | 6 | 2 |
| 2 | Действительные числа
| 9 | 5 | 1 |
| 3 | Функция у = √х Свойства квадратного корня | 7 | 3 | 1 |
| 4 | Квадратичная функция. Функция у= к/х | 9 | 5 | 1 |
| 5 | Квадратные уравнения
| 15 | 6 | 2 |
| 6 |
Неравенства
| 7 | 4 |
1 |
| 7 | Случайные события и их вероятности
| 3 |
| 1
|
| 8 | Повторение | 3 |
1 | 1
|
| Итого | 68 | 25 | 10 |
СОДЕРЖАНИЕ ТЕМ УЧЕБНОЙ ПРОГРАММЫ
Алгебраические дроби. Арифметические операции
над алгебраическими дробями (14)
Алгебраическая дробь, сокращение дробей. Действия с алгебраическими дробями: сложение и вычитание алгебраических дробей с одинаковым знаменателем, с разными знаменателями, умножение и деление алгебраических дробей, возведение алгебраической дроби в степень. Рациональные выражения и их преобразования. Решение рациональных уравнений.
В результате изучения темы обучающиеся должны
знать:
основные понятия темы;
определение рациональных выражений;
как сокращаются дроби;
как складываются и вычитаются дроби с одинаковыми и разными знаменателями;
как умножаются и делятся дроби;
алгоритм решения рациональных уравнений;
уметь:
выполнять арифметические действия над алгебраическими дробями;
выполнять тождественные преобразования рациональных выражений;
находить значение рационального выражения;
решать простейшие рациональные уравнения;
сокращать алгебраические дроби;
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
Контрольная работа 1 «Вводная контрольная работа»
Контрольная работа 2 «Преобразование рациональных выражений»
2. Действительные числа (9)
Рациональные числа. Понятие об иррациональном числе, иррациональность числа. Множество действительных чисел. Действительные числа как бесконечные десятичные дроби. Сравнение действительных чисел, арифметические действия над ними. Этапы развития представлений о числе. Числовая прямая. Модуль действительного числа, его свойства, график функции у = /х/. приближённое значение числа. Округление чисел. Погрешность, прикидка и оценка результатов вычислений. Степень с отрицательным целым показателем. Стандартный вид числа. Выделение множителя – степени десяти в записи числа.
В результате изучения темы обучающиеся должны
знать:
уметь:
находить десятичные приближения иррациональных чисел;
сравнивать действительные числа;
выполнять арифметические действия над действительными числами;
округлять числа;
прикидывать и оценивать результаты вычислений;
выделять множитель – степень десяти в записи числа
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи;
поиска, систематизации, анализа и классификации информации.
Контрольная работа 3 «Действительные числа. Степень с отрицательным целым показателем»
3.Функция у = √ х. Свойства квадратного корня (8)
Квадратный корень из неотрицательного числа. Функция у=√ х, ее свойства и график Использование графиков функций для решения уравнений и систем.
Свойства квадратных корней и их применение в вычислениях.
Преобразование выражений, содержащих квадратные корни. Корень третьей степени.. График функции корень квадратный, корень кубический.
В результате изучения темы обучающиеся должны
знать:
алгоритм построения графика функции у=√ х;
свойства квадратичного корня и функции у=√ х;;
алгоритм графического способа решения уравнений, содержащих квадратные корни ;
как функция у=√ х описывает реальные зависимости; приводить примеры такого описания;
построение и чтение графиков кусочных функций;
уметь:
вычислять значения квадратного корня;
преобразовывать выражения, содержащие квадратные корни;
строить график функции у=√ х;
выполнять преобразования графиков;
осуществлять в выражениях и формулах числовые подстановки и выполнять вычисления;
находить значения функции, заданной формулой, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или формулой;
определять свойства функции по ее графику;
применять графические представления при решении уравнений;
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам;
интерпретации графиков реальных зависимостей между величинами;
анализа реальных числовых данных, представленных в виде графиков, таблиц;
Контрольная работа 4 «Функция у=√ х,. Преобразование иррациональных уравнений»
4.Квадратичная функция. Функция у=к/х (10)
Функция у = ах2, ее свойства и график. Парабола. Функция (у = k/x) описывающая обратную пропорциональную зависимость, ее график. Гипербола. Параллельный перенос графиков вдоль осей координат: (построение графика функции у = f(x + t) по известному графику функции у = f(x)). Построение графика функции у = f(x) + т по известному графику функции у = f(x), по известному графику функции у = f(x)).. Построение графика функции у = f (x + t) + т, по известному графику функции у = f(x)). Квадратичная функция у = ах2+ Ьх +с., её график. Координаты вершины параболы. Ось симметрии. Наибольшее и наименьшее значение квадратичной функции на заданном промежутке ,Использование графиков функций для решения уравнений.
В результате изучения темы обучающиеся должны
знать:
основные понятия темы;
алгоритм построения графика квадратичной функции и функции у=к/х;
свойства квадратичной функции и функции у=к/х;
алгоритм графического способа решения квадратных уравнений;
как функции у = х2 описывает реальные зависимости; приводить примеры такого описания;
построение и чтение графиков кусочных функций;
уметь:
строить график квадратичной функции и функции у=к/х;
осуществлять в выражениях и формулах числовые подстановки и выполнять вычисления;
находить значения функции, заданной формулой, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или формулой;
определять свойства функции по ее графику;
применять графические представления при решении уравнений;
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам;
интерпретации графиков реальных зависимостей между величинами;
анализа реальных числовых данных, представленных в виде графиков, таблиц;
Контрольная работа 5 «Функция у= к х2,
Контрольная работа 6 «Свойства и график функции у = ах2 + Ьх + с
5. Квадратные уравнения (15)
Многочлены с одной переменной. Квадратное уравнение. Формулы корней квадратного уравнения. Примеры решения уравнений в целых числах решение рациональных уравнений, примеры решения уравнений высших степеней: метод замены переменной. Решение текстовых задач алгебраическим способом. Ещё одна формула корней квадратного уравнения. Квадратный трёхчлен. Теорема Виета. Разложение квадратного трёхчлена на линейные множители. Метод разложения на множители Иррациональные уравнения. Равносильность уравнений и равносильные преобразования уравнений .
В результате изучения темы обучающиеся должны
знать:
алгоритм решения неполного квадратного уравнения;
различные методы решения квадратных уравнений;
формулы нахождения корней квадратного уравнения;
формулу разложения квадратного трехчлена на множители
алгоритм нахождения корней рациональных уравнений;
теорему Виета и теорему ей обратную;
уметь:
распознавать квадратное уравнение;
применять алгоритм решения неполного квадратного уравнения для решения уравнений;
применять формулы нахождения корней квадратного уравнения при решении квадратных уравнений;
применять алгоритм нахождения корней рациональных уравнений при решении уравнений;
применять теорему обратную теореме Виета при решении уравнений;
использовать квадратные уравнения к решению математических задач;
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами, при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
Контрольная работа 7 «Квадратные уравнения»
Контрольная работа 8 «Рациональные уравнения»
6. Неравенства (7)
Неравенство с одной переменной. Числовые неравенства и их свойства. Решение неравенства. Линейное неравенство с одной переменной. Квадратное неравенство. Возрастание и убывание функции. Исследование функций на монотонность (с использованием свойств числовых неравенств).
В результате изучения темы обучающиеся должны
знать:
уметь:
решать линейные, квадратные неравенства;
определять свойства функции по ее графику; применять графические представления при решении неравенств;
описывать свойства изученных функций;
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
интерпретации графиков реальных зависимостей между величинами.
распознавания логически некорректных рассуждений;
анализа реальных числовых данных, представленных в виде графиков;
Контрольная работа 9 «Неравенства»
7. Случайные события и их вероятности (3)
Частота события, вероятность. Равновозможные события и подсчет их вероятности. Представление о геометрической вероятности.
В результате изучения темы обучающиеся должны
знать:
вероятностный характер многих закономерностей окружающего мира;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь:
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения учебных и практических задач, требующих систематического перебора вариантов;
сравнения шансов наступления случайных событий, для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений;
УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН
«Геометрия»
8 класс
| № п\п | Тема | Количество часов | В том числе |
| Самостоятельные работы | Контрольные работы |
| 1 | Четырехугольники | 8 | 3 | 1 |
| 2 | Площади фигур | 8 | 3 | 1 |
| 3 | Подобные треугольники | 8 | 4 | 2 |
| 4 | Окружность
| 9 | 4 | 1 |
|
| Итоговая работа | 1 |
|
|
| Итого | 34 | 14 | 5 |
СОДЕРЖАНИЕ ТЕМ УЧЕБНОЙ ПРОГРАММЫ
Вводное повторение (1)
Четырехугольники (8)
Многоугольники. Периметр многоугольника. Выпуклые многоугольники. Правильные многоугольники. Сумма углов выпуклого многоугольника. Параллелограмм и трапеция, их свойства и признаки. Теорема Фалеса. Деление отрезка на n-равных частей. Трапеция. Средняя линия трапеции. Равнобедренная трапеция. Прямоугольник, квадрат, ромб, их свойства и признаки. Осевая и центральная симметрии.
В результате изучения данной главы обучающиеся должны
знать:
определения рассматриваемых четырехугольников, их элементы;
формулировки и доказательства теорем, выражающих признаки и свойства этих четырехугольников;
определения симметричных точек и фигур относительно прямой и точки;
уметь:
распознавать на рисунке и по определению четырехугольники;
применять признаки в решении задач;
строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией;
решать задачи на построение;
использовать приобретённые знания и умения в практической деятельности для:
описания реальных ситуаций на языке геометрии;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства)
построения геометрическими инструментами (линейка, угольник, транспортир)
Контрольная работа №1
Площадь (8)
Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры.
Площадь прямоугольника. Площадь параллелограмма, треугольника и трапеции (основные формулы).
Теорема Пифагора. Формула Герона. Площадь четырехугольника.
В результате изучения данной главы обучающиеся должны
знать:
основные свойства площади;
формулы площади прямоугольника, параллелограмма, треугольника, трапеции;
формулировки теоремы Пифагора и обратной к ней теоремы;
уметь:
выводить формулы площадей изучаемых фигур, доказывать их и применять в решении задач;
доказывать и применять при решении задач теорему Пифагора и обратную ей теорему;
использовать приобретённые знания и умения в практической деятельности для:
описания реальных ситуаций на языке геометрии;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построения геометрическими инструментами (линейка, угольник, транспортир)
Контрольная работа №2
Подобные треугольники (8)
Подобие треугольников; коэффициент подобия. Связь между площадями подобных фигур. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач.Средняя линия треугольника. Применение подобия к доказательству теорем и решению задач.
Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0˚ до 180˚. Основное тригонометрическое тождество. Решение прямоугольных треугольников.
В результате изучения данной главы обучающиеся должны
знать:
определения пропорциональных отрезков, подобных треугольников,
формулировки и доказательства теорем, выражающих признаки и свойства подобных треугольников;
определения синуса, косинуса, тангенса острого угла прямоугольного треугольника;
уметь:
воспроизводить доказательства признаков подобия треугольников;
доказывать основное тригонометрическое тождество;
применять их в решении задач;
использовать приобретённые знания и умения в практической деятельности для:
описания реальных ситуаций на языке геометрии;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построения геометрическими инструментами (линейка, угольник, транспортир)
решения геометрических задач с использованием тригонометрии.
Контрольная работа № 3
Контрольная работа № 4
Окружность (9)
Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности; равенство касательных, проведенных из одной точки.
Центральный, вписанный угол; величина вписанного угла. Метрические соотношения в окружности: свойства секущих, касательных, хорд. Соответствие между величиной угла и длиной дуги окружности .
Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан.. Свойства серединного перпендикуляра. Биссектриса угла, её свойства.
Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные четырёхугольники. Вписанные и описанные окружности правильного многоугольника.
В результате изучения данной главы обучающиеся должны
знать:
случаи взаимного расположения прямой и окружности;
определение, свойство и признак касательной;
определения центрального, вписанного углов, теорему о вписанном угле и следствия из нее;
какая окружность называется вписанной, описанной, теоремы о свойствах окружностей;
уметь:
использовать приобретённые знания и умения в практической деятельности для:
описания реальных ситуаций на языке геометрии;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построения геометрическими инструментами (линейка, угольник, циркуль, транспортир)
КОНТРОЛЬ УРОВНЯ ОБУЧЕННОСТИ
Вводная контрольная работа
Выбери один правильный ответ.
Упростить выражение: х8· (х2)2
а) х3 б) х12 в) х10 г) х13
Графиком какой из указанных функций является прямая?
а) у = х2 -9
б) у=7х+4
в) у= 23/ 5х
г) у= х3+7х
Упростите выражение: 11х + 2ху — 3(х + 3ху).
а) 8х - 3ху
б) 14х + 9ху
в) 8х- 7ху
Из предложенных четырёх пар чисел (а; b) выбери ту, которая является недопустимой для алгебраической дроби
2а2 + 3аb — b3
b2 — 9а2
а) (3;1) б) (2;1) в) (0;3) г) (1;3)
Какое из четырёх равенств не является тождеством
1) х2 — 27 = (х — 3)(х2 + 3х + 9);
2) х3 + 8 = (х + 2)(х2 + 2х + 4);
3) х2 — 6х + 9 = (х — 3)2;
4) х2 + 8ху + 16у2 = (х + 4у)2?
а) 1 б) 2 в) 3 г) 4
Вычислите наиболее удобным способом:
742 — 262
612 — 112
а) 4/3 б) 3/4 в) 2/3 г) 3/2
В треугольнике АВС угол А=700, угол С=550 , ВМ-высота данного треугольника. Найдите углы : МВС и АВС?
а) 700 ; 550 б) 550 ; 350 в) 350; 700 г) 1100; 700
8. Отрезки АВ и СД пересекаются в точке О каждая является серединой каждой из
них. Найти угол ОАС, если угол ОДВ =20 0, угол АОС = 1150
а) 200 б) 450 в) 1150 г) 1350
9. В равнобедренном треугольнике с периметром 64см одна из сторон равна 16см .
Найти длину боковой стороны?
а) 16см б) 32см в) 24см г) 48см
Контрольная работа за 1 полугодие
- 1) Найдите значение алгебраической дроби (2a2 + 4ab+b5)/(2b- a), если а= - 1, b= 2.
а) -5; б) 25/3; в) -25/3; г) 5,2
2) Упростите выражение a2/(a - b) - b2/(a - b)
а) 2(a+b); б) a+b; в) a – b; г) a2b2/(a – b)
- 3) Найдите наименьшее значение функции у=3/х на отрезке [ -4; -0,5]
а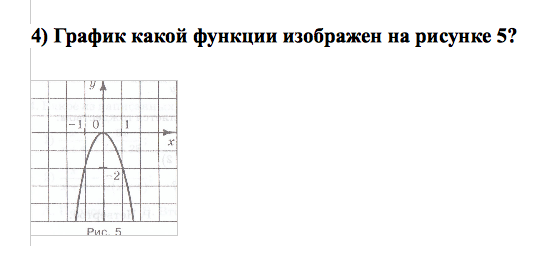
) -3/4; б) 3/4; в) -6; г) не существует
а) у= -2/х; б) у= 2х2 в) у= -х2 г) у=-2х2
- 5) Дана функция у=f(х), где f(х)=3х2+11х - 14. Какое из нижеуказанных значений является положительным числом?
а) f(-1); б) f(-2); в) f(2); г) f(0)
- 6) Какая линия является графиком функции у= - (х-3)2 +2?
а) Прямая, проходящая через начало координат.
б) Прямая, не проходящая через начало координат.
в) Парабола.
г) Гипербола.


9)В параллелограмме разность смежных сторон равна 5 см, а его периметр равен 38 см. Чему равна меньшая сторона параллелограмма?
а) 7 см ; б) 12 см ; в) 9 см ; г) 9.5 см
10) Найдите площадь прямоугольной трапеции, у которой меньшие стороны равны по 12 см каждая, а наибольший угол равен 135 .
.
а) 216 см2; б) 144 см2 в) 72 см2 г) 48 см2.
Перечень литературы и средств обучения
Ссылки на печатные источники:
Александрова JI.A. Алгебра. 8 кл.: Самостоятельные работы для общеобразовательных учреждений.: учреждений. Учеб. Пособие /Под ред. А.Г. Мордковича. 2-е изд. - М.: Мнемозина, 2006. - 80 с.
Дудницин Ю.П., Тульчинская Е.Е. Алгебра. 8 кл.: Контрольные работы / Под ред. А.Г. Мордковича. - 3-е изд., доработанное - М.: Мнемозина, 2001. - 47 с.
Мордкович А.Г. Алгебра 7-9 кл.: методическое пособие для учителя. - 2-е изд., доработанное. - М.: Мнемозина, 2001. - 144 с.
Мордкович А.Г. События. Вероятности. Статистическая обработка данных: Доп. Параграфы к курсу алгебры 7-9 кл. общеобразоват. Учреждений / А.Г.Мордкович, П.В. Семёнов. - 4-е изд. - М.: Мнемозина, 2006. - 112 с.
Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.1:Учебник для общеобразовательных учреждений. - 7-е изд., перераб. - М.: Мнемозина, 2005.
235 с.
Мордкович А.Г. Алгебра. 8 кл.: В двух частях. ч.2: Задачник для общеобразовательных учреждений.- 7-е изд., доработанное. - М.: Мнемозина, 2005.
Л. С. Атанасян, В. Ф. Бутузов. Ю. А. Глазков, В. Б. Некрасов, И. И. Юдина Изучение геометрии в 7-9 классах. Методические рекомендации.- М.: Просвещение 1997 г.
Л. С. Атанасян, В. Ф. Бутузов. С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина Геометрия 7-9 класс. Учебник- М.: Просвещение
Б.Г. Зив. Дидактические материалы по геометрии для 8 класса- М. Просвещение, 2003.
В.Ф. Бутузов, Ю.А. Глазков, И.И. Юдина. Рабочая тетрадь по геометрии для 8 класса. –М.:Просвещение,2003.
Б.Г. Зив, В.М. Мейлер, А.П. Баханский. Задачи по геометрии для 7-11 классов. – М.Просвещение,2003.
Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 8 класса. – 4-е изд. – М. : Просвещение, 1998. (7 класс, 8 класс, 9 класс)
Гусев В.А., Медяник А.И. Дидактические материалы по геометрии для 8 класса. – 4-е изд. – М. : Просвещение, 1995. (7 класс. 8 класс, 9 класс)
Ссылки на электронные ресурсы:
http://www.uroki.net/docmat.htm
http://kolpinoschool648.narod.ru/uchebnaya/matematika/prezentatsii/
http://www.uchportal.ru/load/25-1-0-1179012.
Приложение 1
КАЛЕНДАРНО - ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
МОДУЛЬ « АЛГЕБРА» 8 КЛАСС (68 ЧАС)
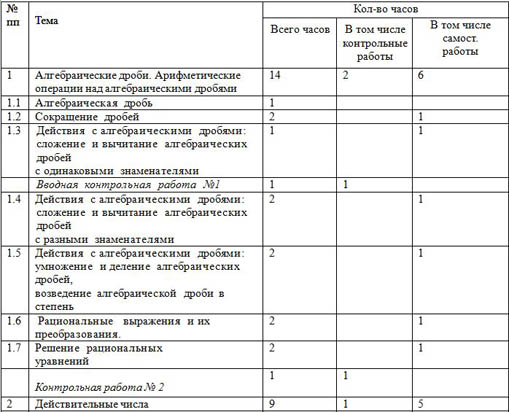
| № пп | - Тема
| Кол-во часов |
| Всего часов | В том числе контрольные работы | В том числе самост. работы |
| 1 | Алгебраические дроби. Арифметические операции над алгебраическими дробями | 14 | 2 | 6 |
| 1.1 | Алгебраическая дробь | 1 |
|
|
| 1.2 | Сокращение дробей | 2 |
| 1 |
| 1.3 | Действия с алгебраическими дробями: сложение и вычитание алгебраических дробей с одинаковыми знаменателями | 1 |
| 1 |
|
| Вводная контрольная работа №1 | 1 | 1 |
|
| 1.4 | Действия с алгебраическими дробями: сложение и вычитание алгебраических дробей с разными знаменателями | 2 |
| 1 |
| 1.5 | Действия с алгебраическими дробями: умножение и деление алгебраических дробей,
возведение алгебраической дроби в степень | 2 |
| 1 |
| 1.6 | Рациональные выражения и их преобразования. | 2 |
| 1 |
| 1.7 | Решение рациональных
уравнений | 2 |
| 1 |
|
| Контрольная работа № 2 | 1 | 1 |
|
| 2 | Действительные числа | 9 | 1 | 5 |
| 2.1
| Рациональные числа. | 1 |
|
|
| 2.2
| Понятие об иррациональном числе, иррациональность числа | 1 |
| 1 |
| 2.3
| Множество действительных чисел. Действительные числа как бесконечные десятичные дроби. Сравнение действительных чисел, арифметические действия над ними. Этапы развития представлений о числе. | 1 |
| 1 |
| 2.4 | Числовая прямая. Модуль действительного числа, его свойства, график функции у =/х/. | 2 |
| 1 |
| 2.5 | Приближенное значение числа. Округление чисел. Погрешность,прикидка и оценка результатов вычислений. | 1 |
|
|
| 2.6 | Степень с отрицательным целым показателем. | 1 |
| 1 |
| 2.7 | Стандартный вид числа. Выделение множителя – степени десяти в записи числа. | 1 |
| 1 |
|
| Контрольная работа № 3 | 1 | 1 | 1 |
| 3 | Функция у = √х Свойства квадратного корня | 8 | 1 | 3 |
| 3.1 | Квадратный корень из неотрицательного числа | 1 |
|
|
| 3.2 | Функция у = √х ,ее свойства и график. Использование графиков функций для решения уравнений и систем. | 1 |
| 1 |
| 3.3 | Свойства квадратных корней и их применение в вычислениях. | 2 |
| 1 |
| 3.4 | Преобразование выражений, содержащих квадратные корни. Корень третьей степени. Графики функций корень квадратный, корень кубический. | 3 |
| 1 |
|
| Контрольная работа № 4 | 1 | 1 |
|
| 4 | Квадратичная функция. Функция у= к/х | 9 | 1 | 5 |
| 4.1 | Функция у = kx2, ее свойства и график. Парабола | 1 |
|
|
| 4.2 | Функция, описывающая обратную пропорциональную зависимость (у = k/x), ее график. Гипербола. | 1 |
| 1 |
| 4.3 | Параллельный перенос графиков вдоль осей координат. Построение графика функции у = f(x +1), у = f(x + t) + m если известен график функции у = f{x) | 1 |
| 1 |
| 4.4 | Параллельный перенос графиков вдоль осей координат. Построение графика функции у = f(x) + m, если известен график функции у = f(x) | 1 |
| 1 |
|
| Контрольная работа №5 | 1 | 1 |
|
| 4.5 | Квадратичная функция у = ах2 + вх + с, её график. Координаты вершины параболы. Ось симметрии .Наибольшее и наименьшее значение квадратичной функции на заданном промежутке. | 1 |
| 1 |
| 4.6 | Использование графиков функций для решения квадратных уравнений | 2 |
| 1 |
|
|
|
|
|
|
| 5 | Квадратные уравнения
| 15 | 2 | 6 |
| 5.1 | Многочлены с одной переменной. ![]() Квадратное уравнение. Квадратное уравнение. | 2 |
| 1 |
| 5.2 | Формулы корней квадратного уравнения. Примеры решения уравнений в целых числах. | 3 |
| 1 |
|
| Контрольная работа №6 | 1 | 1 |
|
| 5.3 | Решение рациональных уравнений, примеры решения уравнений высших степеней: метод замены переменной. | 2 |
| 1 |
| 5.4 | Решение задач алгебраическим способом. | 2 |
| 1 |
| 5.5 | Еще одна формула корней квадратного уравнения Квадратный трёхчлен. Теорема Виета. Разложение квадратного трехчлена на линейные множители. Метод разложения на множители. | 2 |
| 1 |
| 5.6 | Иррациональные уравнения. Равносильность уравнений и равносильные преобразования уравнений. | 2 |
| 1 |
|
| Контрольная работа № 7 | 1 | 1 |
|
| 6 | Неравенства | 7 | 1 | 4 |
| 6.1 | Неравенство с одной переменной. Числовые неравенства и их свойства. Решение неравенства. | 2 |
| 1 |
| 6.2 | Линейное неравенство с одной переменной. | 1 |
| 1 |
| 6.3 | Квадратное неравенство | 2 |
| 1 |
| 6.4 | Возрастание и убывание функции. Исследование функций на монотонность (с использованием свойств числовых неравенств). | 1 |
| 1 |
|
| Контрольная работа №8 | 1 | 1 | 1 |
| 7 | Случайные события и их вероятности | 3 |
| 1 |
| 7.1 | Частота события., вероятность. Равновозможные события и подсчет их вероятности. | 1 |
|
|
| 7.2 | Представление о геометрической вероятности | 2 |
| 1 |
| 8 | Повторение | 3 | 1 | 1 |
| 8.1 | Рациональные дроби | 1 |
|
|
| 8.2 | Квадратные корни и уравнения |
|
|
|
| 8.3 | Неравенства |
|
|
|
| 8.4 | Степень с целым показателем | 1 |
|
|
|
| Итоговая контрольная работа №9 | 1 | 1 |
|
|
| Итого | 68 | 9 | 31 |
Приложение 2
КАЛЕНДАРНО-ТЕМАТИЧЕСКИЙ ПЛАНИРОВАНИЕ
«Геометрия - 8 класс»
| № п/п | Наименование разделов и тем | Всего часов | В том числе контрольные работы | В том числе самост. работы |
| 1 | Четырехугольники | 8 | 1 | 3 |
| 1.1 | Многоугольники. Периметр многоугольника. Выпуклые многоугольники. Правильные многоугольники. Сумма углов выпуклого многоугольника. | 1
|
| 1 |
| 1.2 | Параллелограмм и трапеция, их свойства и признаки. Теорема Фалеса. Деление отрезка на n равных частей. Трапеция. Равнобедренная трапеция. | 3
|
| 1 |
| 1.3 | Прямоугольник, квадрат, ромб, их свойства и признаки. Осевая и центральная симметрии. | 2
|
| 1 |
| 1.4 | Решение задач | 1 |
|
|
|
| Контрольная работа №1 | 1 |
|
|
| 2 | Площади фигур | 8 | 1 | 3 |
| 2.1 | Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры. | 1
|
| 1 |
| 2.2 | Площадь прямоугольника. Площадь параллелограмма, треугольника и трапеции (основные формулы). | 3
|
| 1 |
| 2.3 | Теорема Пифагора. Формула Герона. Площадь четырехугольника. |
2 |
| 1 |
| 2.4 | Решение задач | 1 |
|
|
| 2.5 | Контрольная работа№2 | 1 |
|
|
| 3 | Подобные треугольники | 8 | 2 | 4 |
| 3.1 | Подобие треугольников; коэффициент подобия. Связь между площадями подобных фигур. | 1
|
| 1 |
| 3.2 | Признаки подобия треугольников. | 2 |
| 1 |
|
|
|
|
|
|
| 3.3 | Средняя линия треугольника Применение подобия к доказательству теорем и решению задач. | 1 |
| 1 |
| 3.4 | Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0˚ до 180˚. Основное тригонометрическое тождество. Решение прямоугольных треугольников. |
2
|
| 1 |
| 3.4 | Решение задач | 1 |
|
|
|
| Контрольная работа №3 | 1 |
|
|
| 4 | Окружность
| 9
| 1 | 4 |
|
4.1 | Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности; равенство касательных, проведенных из одной точки. |
2 |
| 1 |
|
4.2 | Центральный, вписанный угол; величина вписанного угла. Метрические соотношения в окружности: свойства секущих, касательных, хорд. Соответствие между величиной угла и длиной дуги окружности. |
2
|
| 1 |
|
4.3
| Замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан.. Свойства серединного перпендикуляра. Биссектриса угла, её свойства. |
1
|
| 1 |
| 4.4 | Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные четырехугольники. Вписанные и описанные окружности правильного многоугольника. | 2 |
| 1 |
|
| Решение задач | 1 |
|
|
|
| Контрольная работа №4 | 1 |
|
|
|
| Итого | 34 | 5 |
|

 Получите свидетельство
Получите свидетельство Вход
Вход





 .
.








 Рабочая программа по математике (8 класс) (0.3 MB)
Рабочая программа по математике (8 класс) (0.3 MB)
 0
0 1859
1859 116
116 Нравится
0
Нравится
0


