Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 37 г.Смоленска
| «Согласовано» Руководитель МО _____________Волкова Н.В
Протокол № __1_ от «29» августа 2013 г.
| «Согласовано» Заместитель директора школы МБОУ СОШ №37 ____________ Звонарёва ГН.
«2» сентября 2013 г.
| «Утверждено» Директор МБОУ СОШ №37 _____________Г.В.Шуневич
Приказ № 167 от «12» сентября 2013 г.
|
РАБОЧАЯ ПРОГРАММА ПО МАТЕМАТИКЕ
для 10 класса
преподавание предмета на профильном уровне
Учитель Емельяненко Лариса Евгеньевна
2013 - 2014 учебный год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Настоящая программа по математике для 10 класса (профильный уровень) составлена в соответствии с требованиями федерального компонента Государственного образовательного стандарта среднего(полного) общего образования по математике (сборник нормативных документов Математика /Сост. Э.Д.Днепров, А.Г.Аркадьев – 2е изд. –М.:Дрофа-2007 г.), примерной программы для общеобразовательных учреждений по алгебре и началам математического анализа к УМК «Алгебра - 10 класс. Профильный уровень - автор А.Г.Мордкович» [Программы для общеобразовательных учреждений. Алгебра и начала математического анализа. 10-11 классы. Авторы-составители И.И.Зубарева, А.Г.Мордкович – М.: Мнемозина, 2007.] и примерной программы общеобразовательных учреждений. Геометрия. 10-11 классы. Сост. Бурмистрова Т.А.-М.: Просвещение, 2008г.
Рабочая содержит в себе два предмета алгебра и начала анализа и геометрия,
программа конкретизирует содержание предметных тем образовательного стандарта и показывает распределение учебных часов по разделам курса. Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение алгебры и началам математического анализа в 10 (профильный уровень) классе отводится 136 часов из расчёта 4 часа в неделю. Рабочая программа по алгебре для 10 класса рассчитана на это же количество часов.
Общая характеристика учебного предмета.
В профильном курсе содержание образования, представленное в основной школе, развивается в следующих направлениях:
• систематизация сведений о числах; формирование представлений о расширении числовых множеств от натуральных до комплексных как способе построения нового математического аппарата для решения задач окружающего мира и внутренних задач математики; совершенствование техники вычислений;
• развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств, систем;
• систематизация и расширение сведений о функциях, совершенствование графических умений; знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи;
• расширение системы сведений о свойствах плоских фигур, систематическое изучение свойств пространственных тел, развитие представлений о геометрических измерениях;
• развитие представлений о вероятностно-статистических закономерностях в окружающем мире;
• совершенствование математического развития до уровня, позволяющего свободно применять изученные факты и методы при решении задач из различных разделов курса, а также использовать их в нестандартных ситуациях;
• формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе
Цели и задачи обучения. формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно - научных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.
Задачи:
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе и его применение к решению математических и нематематических задач;
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
изучение свойств пространственных тел, формирование умения применять полученные знания для решения практических задач;
развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
знакомство с основными идеями и методами математического анализа.
Место предмета в учебном процессе.
Математическое образование играет важную роль, как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формированием способов деятельности, духовная — с интеллектуальным развитием человека, формированием характера и общей культуры.
Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения — от простейших, усваиваемых в непосредственном опыте, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, находить в справочниках нужные формулы и применять их, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виду таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.
Без базовой математической подготовки невозможно стать образованным современным человеком. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни является непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, все больше специальностей, где необходим высокий уровень образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и др.). Таким образом, расширяется круг школьников, для которых математика становится значимым предметом.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления и воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач — основной учебной деятельности на уроках математики — развиваются творческая и прикладная стороны мышления.
Обучение математике дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом общей культуры в современном толковании является общее знакомство с методами познания действительности, представление о предмете и методе математики, его отличия от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.
Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии.
Межпредметные связи.
Математика, неоспоримо, является фундаментальной наукой и имеет широкое применение в самых различных областях науки и техники. Среди школьных предметов она является базой для предметов естественного цикла. Такие темы, как действия с обыкновенными и десятичными дробями, степени, формулы, функции, масштаб, уравнения широко применяются при решении практических задач физики, химии, биологии, географии, астрономии, информатики, экономики.
Предметы естественно-математического цикла дают учащимся знания о живой и неживой природе, о материальном единстве мира, о природных ресурсах и их использовании в хозяйственной деятельности человека.
Общие учебно-воспитательные задачи этих предметов направлены на всестороннее гармоничное развитие личности. Важнейшим условием решения этих общих задач является осуществление и развитие межпредметных связей предметов, согласованной работы учителей-предметников.
Изучение всех предметов естественнонаучного цикла тесно связано с математикой. Она дает учащимся систему знаний и умений, необходимых в повседневной жизни и трудовой деятельности человека, а также важных для изучения смежных предметов. На основе знаний по математике в первую очередь формируются общепредметные расчетно-измерительные умения. Преемственные связи с курсами естественнонаучного цикла раскрывают практическое применение математических умений и навыков. Это способствует формированию у учащихся целостного, научного мировоззрения.
Особенности организации учебного процесса
Важную роль в учебном процессе играют формы организации обучения или виды обучения, в качестве которых выступают устойчивые способы организации педагогического процесса.
Основной формой организации учебно-воспитательной работы с учащимися в школе является урок ( урок ознакомления с новым материалом, урок закрепления изученного, урок применения знаний и умений, урок обобщения и систематизации знаний, урок проверки и коррекции знаний и умений, комбинированный урок) , однако, начиная с 7 класса, могут быть использованы и другие формы обучения. Применение разнообразных, нестандартных форм обучения должно в первую очередь соответствовать интеллектуальному уровню развития обучающихся и их психологическим особенностям.
К нестандартным формам обучения математики в школе относятся: лекции, семинары, консультации, экскурсии, конференции, практикумы, деловые игры, дидактические игры, уроки-зачеты, работа в группах.
Не менее выжны и формы контроля знаний, умений, навыков (текущий контроль, диагностический, рубежный, итоговый). Формы такого контроля также различны. Это могут быть и контрольные работы, и самостоятельные домашние работы, и защита рефератов и проектов, и переводные экзамены, и индивидуальное собеседование, диагностические работы, а также комплексное собеседование и защита темы.
Для развития у учащихся интереса к изучаемому предмету и, как следствие, повышения качества знаний используются современные инновационные технологии такие, как:
Технология уровневой дифференциации обучения
Технология проблемно-развивающего обучения
Здоровье-сберегающие технологии
Технологии сотрудничества
Игровые технологии
Общеучебные умения, навыки и способы деятельности. Универсальные учебные действия.
В ходе изучения математики в профильном курсе старшей школы учащиеся продолжают овладение разнообразными способами деятельности, приобретают и совершенствуют опыт
проведения доказательных рассуждений, логического обоснования выводов, использования различных языков математики для иллюстрации, интерпретации, аргументации и доказательства;
решения широкого класса задач из различных разделов курса, поисковой и творческой деятельности при решении задач повышенной сложности и нетиповых задач;
планирования и осуществления алгоритмической деятельности: выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; использования и самостоятельного составления формул на основе обобщения частных случаев и результатов эксперимента; выполнения расчетов практического характера;
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин и реальной жизни; проверки и оценки результатов своей работы, соотнесения их с поставленной задачей, с личным жизненным опытом;
самостоятельной работы с источниками информации, анализа, обобщения и систематизации полученной информации, интегрирования ее в личный опыт.
В ходе освоения содержания математического образования учащиеся овладевают системой личностных, регулятивных, познавательных, коммуникативных универсальных учебных действий, построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
выполнение и самостоятельное составление алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
самостоятельная работа с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
проведение доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
самостоятельная и коллективная деятельность, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
- развитие у обучающихся способности к самосознанию, саморазвитию и самоопределению;
- формирование личностных ценностно-смысловых ориентиров и установок, способности их использования в учебной, познавательной и социальной практике;
- самостоятельного планирования и осуществления учебной деятельности и организации учебного сотрудничества с педагогами и сверстниками, к построению индивидуальной образовательной траектории;
- формирование у обучающихся системных представлений и опыта применения методов, технологий и форм организации проектной и учебно-исследовательской деятельности для достижения практико-ориентированных результатов образования;
- формирование навыков разработки, реализации и общественной презентации обучающимися результатов исследования, индивидуального проекта, направленного на решение научной, личностно и (или) социально значимой проблемы.
Содержание программы
Действительные числа(12ч)
Натуральные и целые числа. Делимость чисел. Основная теорема арифметики натуральных чисел. Рациональные, иррациональные, действительные числа, числовая прямая. Числовые неравенства. Аксиоматика действительных чисел. Модуль действительного числа. Метод математической индукции.
Числовые функции (9ч)
Определение числовой функции, способы ее задания, свойства функций. Периодические и обратные функции.
Тригонометрические функции (24ч)
Числовая окружность на координатной плоскости. Синус и косинус. Тангенс и котангенс. Тригонометрические функции числового аргумента. Тригонометрические функции углового аргумента, их свойства и графики. Сжатие и растяжение графиков тригонометрических функций. Обратные тригонометрические функции.
Тригонометрические уравнения (10ч)
Простейшие тригонометрические уравнения. Методы решения тригонометрических уравнений: введение новой переменной, разложение на множители, однородные тригонометрические уравнения.
Преобразование тригонометрических выражений (21ч)
Формулы сложения, приведения, двойного аргумента, понижения степени. Преобразование суммы тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в суммы. Методы решения тригонометрических уравнений (продолжение).
Комплексные числа.(9ч)
Комплексные числа и арифметические операции над ними. Комплексные числа и координатная плоскость. Тригонометрическая форма записи комплексного числа. Комплексные числа и квадратные уравнения. Возведение комплексного числа в степень. Извлечение квадратного и кубического корня из комплексного числа.
Производная (29ч)
Определение числовой последовательности и способы ее задания. Свойства числовых последовательностей.
Определение предела последовательности. Свойства сходящихся последовательностей. Вычисление пределов последовательностей. Сумма бесконечной геометрической прогрессии.
Предел функции на бесконечности. Предел функции в точке. Приращение аргумента. Приращение функции.
Задачи, приводящие к понятию производной. Определение производной. Алгоритм отыскания производной. Формулы дифференцирования. Правила дифференцирования. Понятие производной n-го порядка. Дифференцирование сложной функции. Дифференцирование обратной функции. Уравнение касательной к графику функции. Алгоритм составления уравнения касательной к графику функции y = f(x).
Применение производной для доказательства тождеств и неравенств. Построение графиков функций. Применение производной для отыскания наибольших и наименьших значений непрерывной функции на промежутке. Задачи на оптимизацию.
Комбинаторика и вероятность.(7ч)
Правило умножения. Перестановки и факториалы. Выбор нескольких элементов. Сочетания и размещения. Бином Ньютона. Случайные события и их вероятности.
9. Параллельность прямых и плоскостей (16ч) Параллельные прямые в пространстве. Параллельность трех прямых. Параллельность прямой и плоскости. Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми. Параллельные плоскости. Свойства параллельных плоскостей. Тетраэдр.
10. Перпендикулярность прямых и плоскостей(17ч) Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости. Признак перпендикулярности прямой и плоскости. Теорема о прямой, перпендикулярной к плоскости. Расстояние от точки до плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Двугранный угол. Признак перпендикулярности двух плоскостей. Прямоугольный параллелепипед.
11. Многогранники(14ч) Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб. Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. Сечения куба, призмы, пирамиды. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
12. Вектора (7ч) Понятие вектора. Модуль вектора. Равенство векторов. Коллинеарные векторы.Сложение и вычитание векторов. Сумма нескольких векторов. Умножение вектора на число. Компланарные векторы. Правило параллелепипеда. Разложение вектора по трем некомпланарным векторам.
Результаты процесса обучения
В результате изучения математики на профильном уровне ученик должен
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
возможности геометрического языка как средства описания свойств реальных предметов и их взаимного расположения;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
вероятностных характер различных процессов и закономерностей окружающего мира.
Числовые и буквенные выражения
Уметь:
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
проводить преобразования числовых и буквенных выражений, включающих тригонометрические функции.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, при необходимости используя справочные материалы и простейшие вычислительные устройства.
Функции и графики
Уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
описания и исследования с помощью функций реальных зависимостей, представления их графически;
интерпретации графиков реальных процессов.
Начала математического анализа
Уметь
находить сумму бесконечно убывающей геометрический прогрессии;
вычислять производные элементарных функций, применяя правила вычисления производных, используя справочные материалы;
исследовать функции и строить их графики с помощью производной;
решать задачи с применением уравнения касательной к графику функции;
решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа.
Уравнения и неравенства
Уметь
решать рациональные и тригонометрические уравнения и неравенства, их системы;
доказывать несложные неравенства;
решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учетом ограничений условия задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
построения и исследования простейших математических моделей.
Элементы комбинаторики, статистики и теории вероятностей
Уметь:
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
вычислять, в простейших случаях, вероятности событий на основе подсчета числа исходов.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
анализа реальных числовых данных, представленных в виде диаграмм, графиков;
анализа информации статистического характера.
Геометрия уметь:
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
анализировать в взаимное расположение объектов в пространстве;
изображать основные многогранники; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач;
Критерии и нормы оценки знаний, умений и навыков обучающихся
по алгебре и началам анализа
1. Оценка письменных контрольных работ.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Список литературы для обучающихся.
Алгебра и начала математического анализа. 10 класс. Часть 1.: учебник / А.Г.Мордкович, П.В. Семенов –2е изд. - М.: МНЕМОЗИНА, 2011.
Алгебра и начала математического анализа. 10 класс. Часть 2.: задачник / А.Г.Мордкович и др. –2-е изд. - М.: МНЕМОЗИНА, 2011.
Алгебра и начала математического анализа. Контрольные работы.10 класс профильный уровень / В.И. Глизбург под редакцией А.Г.Мордковича.– М.: Мнемозина, 2012.
Алгебра и начала математического анализа. Самостоятельные работы.10 класс / Л.А.Александрова под редакцией А.Г.Мордковича.– М.: Мнемозина, 2012.
Атанасян Л.С., Бутузов В.Ф. Геометрия в 10-11 класс. М., 2009;
Зив. Б.Г., Мейлер В.М., Баханский А.Г. Задачи по геометрии для 7-11 классов. М., 2005;
Звавич Л.И. Контрольные и проверочные работы по геометрии 10-11 класс. М., 2011;
Список литературы для учителя.
Учебник «Алгебра и начала анализа» 10 класс. Авт.: А.Г. Мордкович, П.В. Семенов–2е изд. - М.: МНЕМОЗИНА, 2011.
Задачник «Алгебра и начала анализа» 10 класс. Авт.: А.Г. Мордкович, Л.О. Денищева, Л.И. Звавич, Т.А. Корешкова, Т.Н. Мишустина, А.Р. Рязановский, П.В. Семенов–2-е изд. - М.: МНЕМОЗИНА, 2011.
Методическое пособие для учителя «Алгебра и начала анализа» 10, 11 классы. Авт.: А.Г. Мордкович, П.В. Семенов
Контрольные работы «Алгебра и начала анализа» 10 класс. Автор В.И. Глизбург профильный уровень
Алгебра и начала математического анализа. Самостоятельные работы.10 класс / Л.А.Александрова под редакцией А.Г.Мордковича.– М.: Мнемозина, 2012. профильный уровень.
Атанасян Л.С., Бутузов В.Ф. Геометрия в 10-11 класс. М., 2009;
Зив. Б.Г., Мейлер В.М., Баханский А.Г. Задачи по геометрии для 7-11 классов. М., 2011;
Звавич Л.И. Контрольные и проверочные работы по геометрии 10-11 класс. М., 2011;
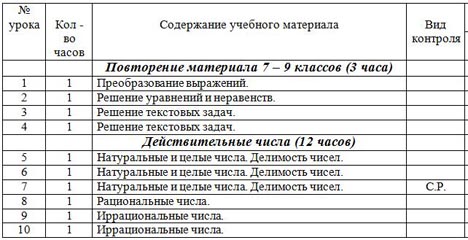
Календарно-тематическое планирование 10 класс (профильный). Годовое количество часов- 204. Количество часов в неделю - 6
Календарно – тематический план
| № урока |
Кол - во часов |
Содержание учебного материала |
Вид контроля | Дата проведения урока |
| 10 А | 10 Б |
|
|
| Повторение материала 7 – 9 классов (3 часа) |
|
|
|
| 1 | 1 | Преобразование выражений. |
|
|
|
| 2 | 1 | Решение уравнений и неравенств. |
|
|
|
| 3 | 1 | Решение текстовых задач. |
|
|
|
| 4 | 1 | Решение текстовых задач. |
|
|
|
|
|
| Действительные числа (12 часов) |
|
|
|
| 5 | 1 | Натуральные и целые числа. Делимость чисел. |
|
|
|
| 6 | 1 | Натуральные и целые числа. Делимость чисел. |
|
|
|
| 7 | 1 | Натуральные и целые числа. Делимость чисел. | С.Р. |
|
|
| 8 | 1 | Рациональные числа. |
|
|
|
| 9 | 1 | Иррациональные числа. |
|
|
|
| 10 | 1 | Иррациональные числа. |
|
|
|
| 11 | 1 | Множество действительных чисел. |
|
|
|
| 12 | 1 | Модуль действительного числа. |
|
|
|
| 13 | 1 | Модуль действительного числа. |
|
|
|
| 14 | 1 | Контрольная работа по теме: "Действительные числа" | К.Р. |
|
|
| 15 | 1 | Метод математической индукции. |
|
|
|
| 16 | 1 | Метод математической индукции. |
|
|
|
|
|
| Аксиомы геометрии и их следствие (6 часов) |
|
|
|
| 17 | 1 | Аксиомы стереометрии. |
|
|
|
| 18 | 1 | Некоторые следствия из аксиом. |
|
|
|
| 19 | 1 | Решение задач. |
|
|
|
| 20 | 1 | Решение задач. |
|
|
|
| 21 | 1 | Решение задач. |
|
|
|
| 22 | 1 | Решение задач. Самостоятельная работа. | С.Р. |
|
|
|
|
| Параллельность прямых, прямых и плоскостей (16 часов) |
|
|
|
| 23 | 1 | Параллельность прямых в пространстве. |
|
|
|
| 24 | 1 | Параллельность прямой и плоскости. |
|
|
|
| 25 | 1 | Решение задач. |
|
|
|
| 26 | 1 | Решение задач. Самостоятельная работа. | С.Р. |
|
|
| 27 | 1 | Взаимное расположение прямых в пространстве. |
|
|
|
| 28 | 1 | Скрещивающиеся прямые. |
|
|
|
| 29 | 1 | Угол между прямыми. |
|
|
|
| 30 | 1 | Решение задач. |
|
|
|
| 31 | 1 | Контрольная работа «Параллельность прямых в пространстве». | К.Р. |
|
|
| 32 | 1 | Параллельные плоскости. Свойства параллельных плоскостей. |
|
|
|
| 33 | 1 | Параллельность плоскостей. Свойства параллельных плоскостей. |
|
|
|
| 34 | 1 | Тетраэдр и параллелепипед |
|
|
|
| 35 | 1 | Тетраэдр и параллелепипед |
|
|
|
| 36 | 1 | Задачи на построение сечений |
|
|
|
| 37 | 1 | Задачи на построение сечений |
|
|
|
| 38 | 1 | Контрольная работа «Тетраэдр и параллелепипед" | К.Р. |
|
|
|
|
| Числовые функции (9 часов) |
|
|
|
| 39 | 1 | Определение числовой функции и способы ее задания. |
|
|
|
| 40 | 1 | Определение числовой функции и способы ее задания. |
|
|
|
| 41 | 1 | Свойства функций. |
|
|
|
| 42 | 1 | Свойства функций. |
|
|
|
| 43 | 1 | Свойства функций. | С.Р. |
|
|
| 44 | 1 | Периодические функции. |
|
|
|
| 45 | 1 | Обратные функции. |
|
|
|
| 46 | 1 | Обратные функции. |
|
|
|
| 47 | 1 | Контрольная работа по теме:"Числовые функции". | К.Р. |
|
|
|
|
| Тригонометрические функции (24 часа) |
|
|
|
| 48 | 1 | Числовая окружность. |
|
|
|
| 49 | 1 | Числовая окружность. |
|
|
|
| 50 | 1 | Числовая окружность на координатной плоскости. |
|
|
|
| 51 | 1 | Числовая окружность на координатной плоскости. |
|
|
|
| 52 | 1 | Синус и косинус. Тангенс и котангенс. |
|
|
|
| 53 | 1 | Синус и косинус. Тангенс и котангенс. | М.Д. |
|
|
| 54 | 1 | Синус и косинус. Тангенс и котангенс. | . |
|
|
| 55 | 1 | Тригонометрические функции числового аргумента. |
|
|
|
| 56 | 1 | Тригонометрические функции числового аргумента. |
|
|
|
| 57 | 1 | Тригонометрические функции углового аргумента. | С.Р |
|
|
| 58 | 1 | Функции 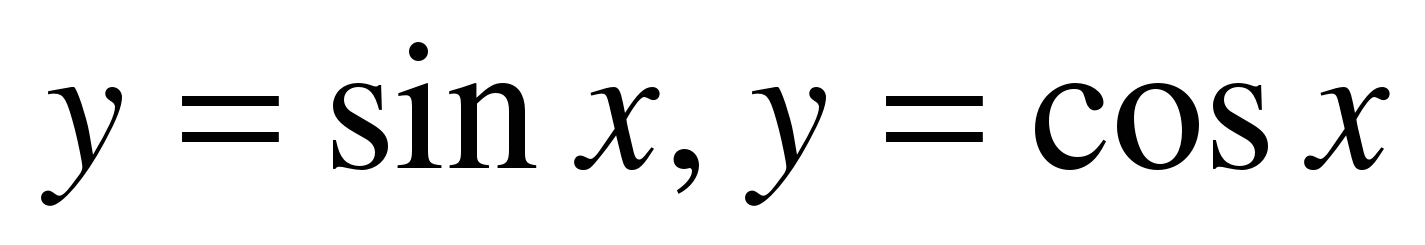 , их свойства и графики. , их свойства и графики. |
|
|
|
| 59 | 1 | Функции 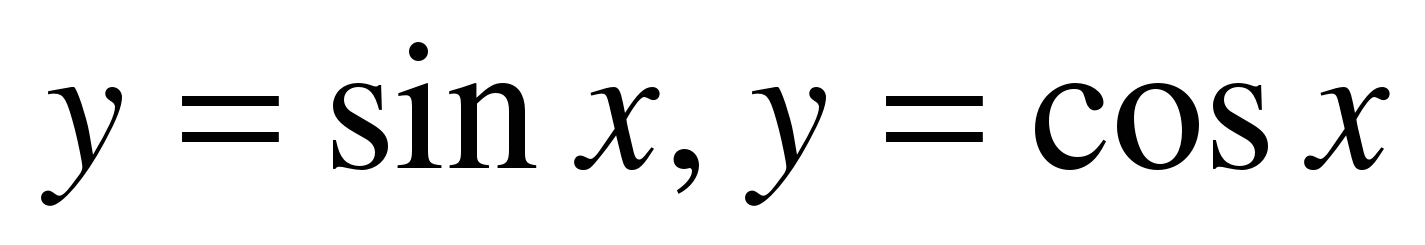 , их свойства и графики. , их свойства и графики. |
|
|
|
| 60 | 1 | Функции 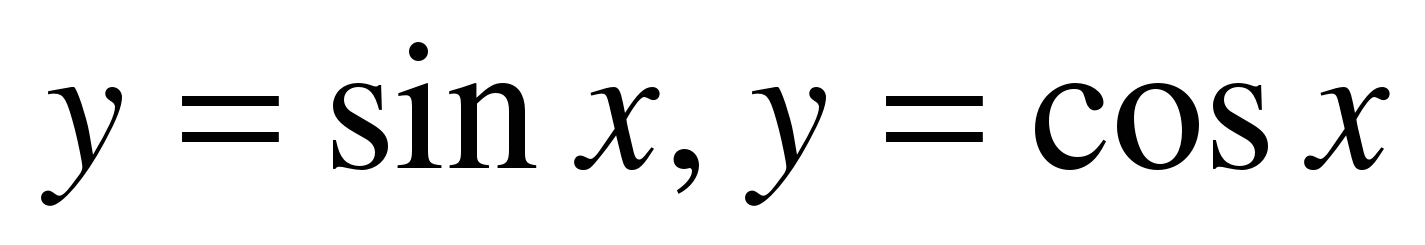 , их свойства и графики. , их свойства и графики. |
|
|
|
| 61 | 1 | Контрольная работа № 3 по теме"Числовая окружность на координатной плоскости". | К.Р. |
|
|
| 62 | 1 | Построение графика функции 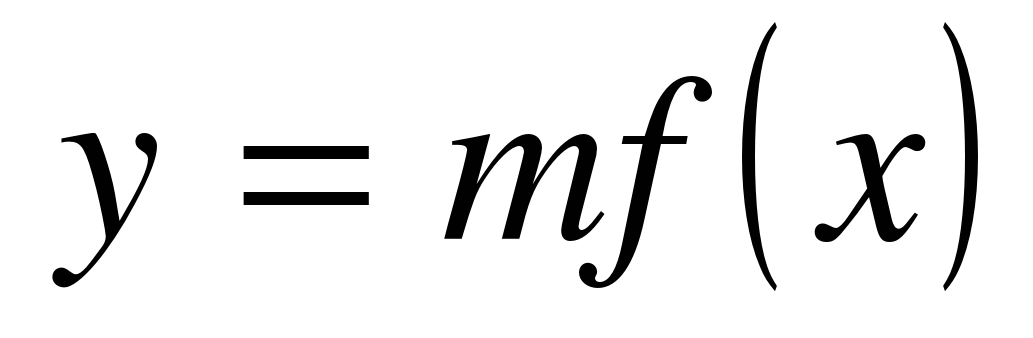 . . |
|
|
|
| 63 | 1 | Построение графика функции 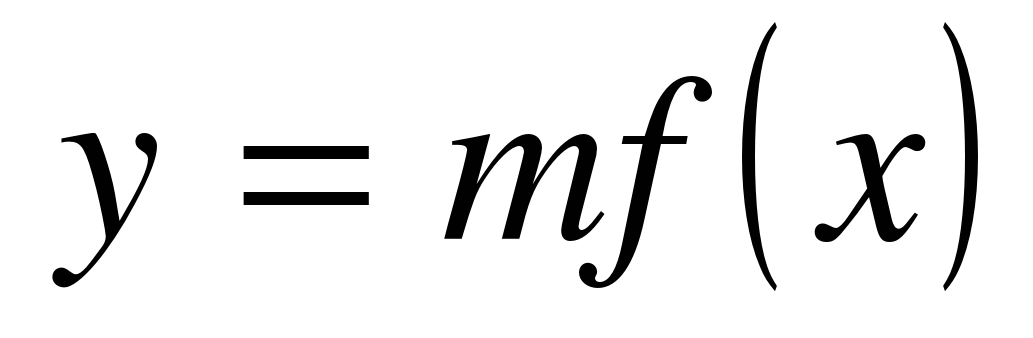 . . |
|
|
|
| 64 | 1 | Построение графика функции 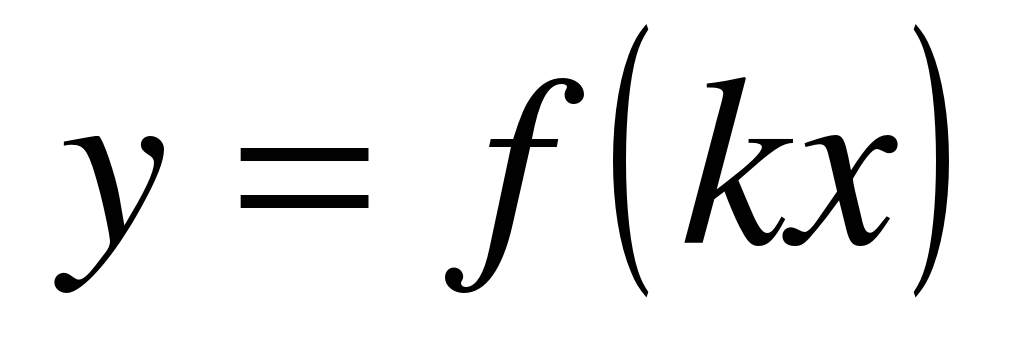 . . |
|
|
|
| 65 | 1 | Построение графика функции 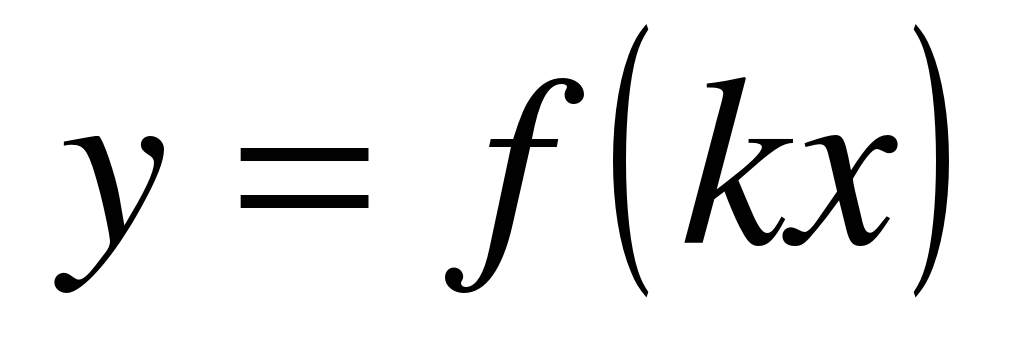 . . | Пр.Р. |
|
|
| 66 | 1 | График гармонического колебания. |
|
|
|
| 67 | 1 | Функции 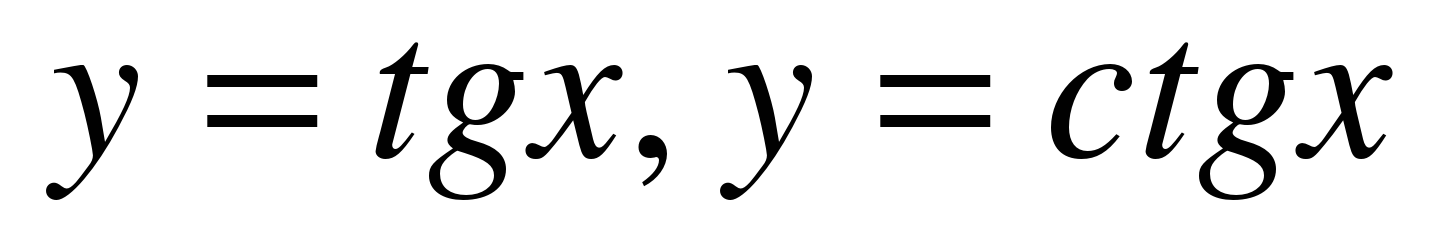 , их свойства и графики. , их свойства и графики. |
|
|
|
| 68 | 1 | Функции 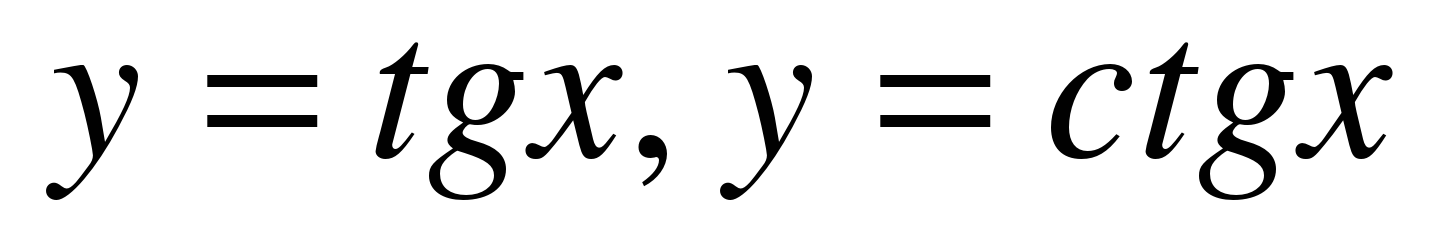 , их свойства и графики. , их свойства и графики. |
|
|
|
| 69 | 1 | Обратные тригонометрические функции. |
|
|
|
| 70 | 1 | Обратные тригонометрические функции. |
|
|
|
| 71 | 1 | Обратные тригонометрические функции. |
|
|
|
|
|
| Перпендикулярность прямых и плоскостей (17 часов) |
|
|
|
| 72 | 1 | Перпендикулярность прямых в пространстве. |
|
|
|
| 73 | 1 | Признак перпендикулярности прямой и плоскости. |
|
|
|
| 74 | 1 | Признак перпендикулярности прямой и плоскости. |
|
|
|
| 75 | 1 | Решение задач. |
|
|
|
| 76 | 1 | Решение задач. Самостоятельная работа. | С.Р |
|
|
| 77 | 1 | Теорема о трех перпендикулярах. |
|
|
|
| 78 | 1 | Теорема о трех перпендикулярах. |
|
|
|
| 79 | 1 | Угол между прямой и плоскостью. |
|
|
|
| 80 | 1 | Решение задач. |
|
|
|
| 81 | 1 | Решение задач. |
|
|
|
| 82 | 1 | Решение задач. Самостоятельная работа. | С.Р |
|
|
| 83 | 1 | Двугранный угол. Признак перпендикулярности двух плоскостей. |
|
|
|
| 84 | 1 | Двугранный угол. Признак перпендикулярности двух плоскостей. |
|
|
|
| 85 | 1 | Прямоугольный параллелепипед. |
|
|
|
| 86 | 1 | Прямоугольный параллелепипед. |
|
|
|
| 87 | 1 | Решение задач. |
|
|
|
| 88 | 1 | Контрольная работа «Перпендикулярность прямых и плоскостей». | К.Р. |
|
|
|
|
| Тригонометрические уравнения (10 часов) |
|
|
|
| 89 |
| Простейшие тригонометрические уравнения и неравенства. |
|
|
|
| 90 |
| Простейшие тригонометрические уравнения и неравенства. |
|
|
|
| 91 |
| Простейшие тригонометрические уравнения и неравенства. |
|
|
|
| 92 |
| Простейшие тригонометрические уравнения и неравенства. | С.Р |
|
|
| 93 |
| Методы решения тригонометрических уравнений. |
|
|
|
| 94 |
| Методы решения тригонометрических уравнений. |
|
|
|
| 95 |
| Методы решения тригонометрических уравнений. | С.Р |
|
|
| 96 |
| Методы решения тригонометрических уравнений. |
|
|
|
| 97 |
| Контрольная работа по теме: "Тригонометрические уравнения". | К.Р. |
|
|
| 98 |
| Контрольная работа: "Тригонометрические уравнения". | К.Р. |
|
|
|
|
| Преобразование тригонометрических выражений (21 час) |
|
|
|
| 99 |
| Синус и косинус суммы и разности аргументов. |
|
|
|
| 100 |
| Синус и косинус суммы и разности аргументов. |
|
|
|
| 101 |
| Синус и косинус суммы и разности аргументов. |
|
|
|
| 102 |
| Тангенс суммы и разности аргументов. |
|
|
|
| 103 |
| Тангенс суммы и разности аргументов. | С.Р |
|
|
| 104 |
| Формулы приведения. |
|
|
|
| 105 |
| Формулы приведения. |
|
|
|
| 106 |
| Формулы двойного аргумента. Формулы понижения степени. |
|
|
|
| 107 |
| Формулы двойного аргумента. Формулы понижения степени. |
|
|
|
| 108 |
| Формулы двойного аргумента. Формулы понижения степени. |
|
|
|
| 109 |
| Преобразование суммы тригонометрических функций в произведение. |
|
|
|
| 110 |
| Преобразование суммы тригонометрических функций в произведение. |
|
|
|
| 111 |
| Преобразование суммы тригонометрических функций в произведение. |
|
|
|
| 112 |
| Преобразование произведения тригонометрических функций в сумму. |
|
|
|
| 113 |
| Преобразование произведения тригонометрических функций в сумму. | С.Р |
|
|
| 114 |
| Преобразование выражения 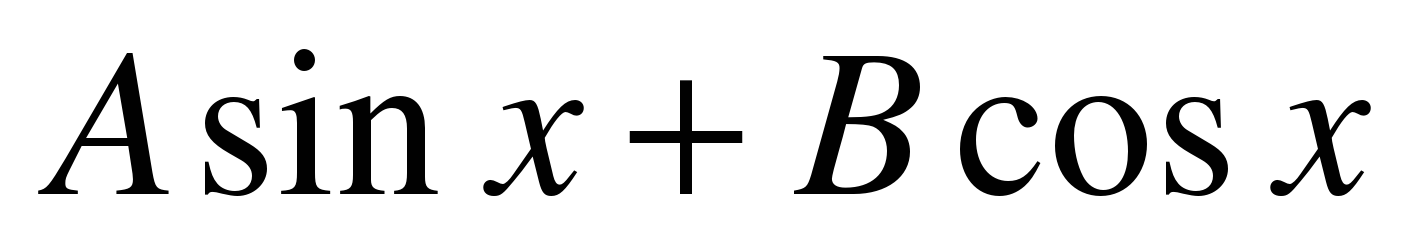 к виду к виду 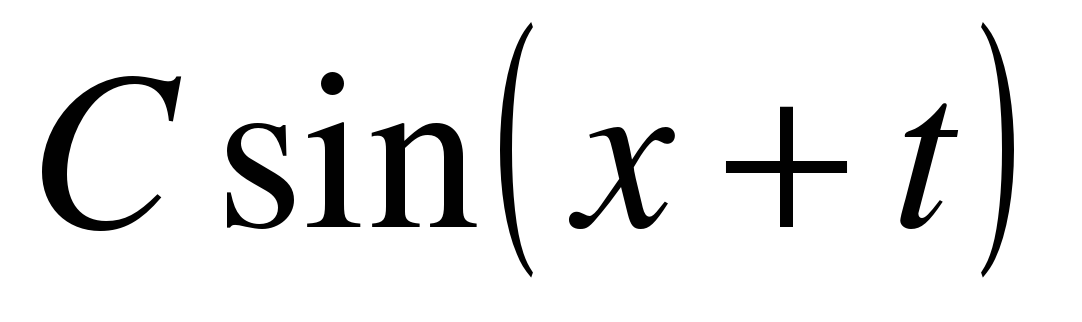 . . |
|
|
|
| 115 |
| Методы решения тригонометрических уравнений. |
|
|
|
| 116 |
| Методы решения тригонометрических уравнений. | Дом. С.Р. |
|
|
| 117 |
| Методы решения тригонометрических уравнений. |
|
|
|
| 118 |
| Контрольная работа по теме:" Преобразование тригонометрических выражений". | К.Р. |
|
|
| 119 |
| Контрольная работа:" Преобразование тригонометрических выражений". | К.Р. |
|
|
|
|
| Многогранники (14 часов) |
|
|
|
| 120 | 1 | Понятие многогранника. Призма. |
|
|
|
| 121 | 1 | Призма.. |
|
|
|
| 122 | 1 | Призма. |
|
|
|
| 123 | 1 | Призма. |
|
|
|
| 124 | 1 | Призма. Самостоятельная работа. | С.Р |
|
|
| 125 | 1 | Пирамида. Правильная пирамида. |
|
|
|
| 126 | 1 | Пирамида. Правильная пирамида. |
|
|
|
| 127 | 1 | Пирамида. Правильная пирамида. |
|
|
|
| 128 | 1 | Усеченная пирамида. |
|
|
|
| 129 | 1 | Пирамида. Самостоятельная работа. | С.Р |
|
|
| 130 | 1 | Симметрия в пространстве. Понятие правильного многогранника. |
|
|
|
| 131 | 1 | Решение задач |
|
|
|
| 132 | 1 | Решение задач |
|
|
|
| 133 | 1 | Контрольная работа «Многогранники». | К.Р. |
|
|
|
|
| Комплексные числа (9 часов) |
|
|
|
| 134 | 1 | Комплексные числа и арифметические операции над ними. |
|
|
|
| 135 | 1 | Комплексные числа и арифметические операции над ними. |
|
|
|
| 136 | 1 | Комплексные числа и координатная плоскость. |
|
|
|
| 137 | 1 | Тригонометрическая форма записи комплексного числа. |
|
|
|
| 138 | 1 | Тригонометрическая форма записи комплексного числа. |
|
|
|
| 139 | 1 | Комплексные числа и квадратные уравнения. |
|
|
|
| 140 | 1 | Возведение комплексного числа в степень. Извлечение кубического корня из комплексного числа. |
|
|
|
| 141 | 1 | Возведение комплексного числа в степень. Извлечение кубического корня из комплексного числа. |
|
|
|
| 142 | 1 | Контрольная работа № 6. | К.Р. |
|
|
|
|
| Производная (29 часов) |
|
|
|
| 143 | 1 | Числовые последовательности. |
|
|
|
| 144 | 1 | Числовые последовательности. |
|
|
|
| 145 | 1 | Предел числовой последовательности. |
|
|
|
| 146 | 1 | Предел числовой последовательности. |
|
|
|
| 147 | 1 | Предел функции. |
|
|
|
| 148 | 1 | Предел функции. | С.Р |
|
|
| 149 | 1 | Определение производной. |
|
|
|
| 150 | 1 | Определение производной. |
|
|
|
| 151 | 1 | Вычисление производных |
|
|
|
| 152 | 1 | Вычисление производных |
|
|
|
| 153 | 1 | Вычисление производных |
|
|
|
| 154 | 1 | Дифференцирование сложной функции. Дифференцирование обратной функции. | С.Р |
|
|
| 155 | 1 | Дифференцирование сложной функции. Дифференцирование обратной функции. |
|
|
|
| 156 | 1 | Уравнение касательной к графику функции. |
|
|
|
| 157 | 1 | Уравнение касательной к графику функции. |
|
|
|
| 158 | 1 | Уравнение касательной к графику функции. |
|
|
|
| 159 | 1 | Контрольная работа по теме:" Производная" | К.Р. |
|
|
| 160 | 1 | Контрольная работа:" Производная" | К.Р. |
|
|
| 161 | 1 | Применение производной для исследования функций. |
|
|
|
| 162 | 1 | Применение производной для исследования функций. |
|
|
|
| 163 | 1 | Применение производной для исследования функций. |
|
|
|
| 164 | 1 | Построение графиков функций. |
|
|
|
| 165 | 1 | Построение графиков функций. | Пр.Р. |
|
|
| 166 | 1 | Применение производной для отыскания наибольших и наименьших значений величин. |
|
|
|
| 167 | 1 | Применение производной для отыскания наибольших и наименьших значений величин. |
|
|
|
| 168 | 1 | Применение производной для отыскания наибольших и наименьших значений величин. |
|
|
|
| 169 | 1 | Применение производной для отыскания наибольших и наименьших значений величин. |
|
|
|
| 170 | 1 | Контрольная работа по теме:"Применение производной" | К.Р. |
|
|
| 171 | 1 | Контрольная работа по теме:"Применение производной" | К.Р. |
|
|
|
|
| Векторы в пространстве (7 часов) |
|
|
|
| 172 | 1 | Понятие вектора. Равенство векторов. |
|
|
|
| 173 | 1 | Понятие вектора. Равенство векторов. |
|
|
|
| 174 | 1 | Сложение и вычитание векторов. Сумма нескольких векторов. Умножение вектора на число. |
|
|
|
| 175 | 1 | Сложение и вычитание векторов. Сумма нескольких векторов. Умножение вектора на число. |
|
|
|
| 176 | 1 | Компланарные векторы. Разложение вектора по трем некомпланарным векторам. |
|
|
|
| 177 | 1 | Компланарные векторы. Разложение вектора по трем некомпланарным векторам. |
|
|
|
| 178 | 1 | Компланарные векторы. Разложение вектора по трем некомпланарным векторам. Самостоятельная работа. | С.Р |
|
|
|
|
| Комбинаторика и вероятность (8 часов) |
|
|
|
| 179 | 1 | Правило умножения. Комбинаторные задачи. Перестановки и факториалы. |
|
|
|
| 180 | 1 | Правило умножения. Комбинаторные задачи. Перестановки и факториалы. |
|
|
|
| 181 | 1 | Правило умножения. Комбинаторные задачи. Перестановки и факториалы. |
|
|
|
| 182 | 1 | Выбор нескольких элементов. Биноминальные коэффициенты. |
|
|
|
| 183 | 1 | Выбор нескольких элементов. Биноминальные коэффициенты. |
|
|
|
| 184 | 1 | Случайные события и их вероятности. |
|
|
|
| 185 | 1 | Случайные события и их вероятности. |
|
|
|
| 186 | 1 | Случайные события и их вероятности. |
|
|
|
|
|
| Повторение (16 часов) |
|
|
|
| 187 | 1 | Преобразование тригонометрических выражений. |
|
|
|
| 188 | 1 | Решение тригонометрических уравнений и неравенств. |
|
|
|
| 189 | 1 | Решение тригонометрических уравнений и неравенств. |
|
|
|
| 190 | 1 | Вычисление производных. |
|
|
|
| 191 | 1 | Применение производной для отыскания наибольших и наименьших значений величин. | К.Р. |
|
|
| 192 | 1 | Итоговая контрольная работа. | К.Р. |
|
|
| 193 | 1 | Итоговая контрольная работа. |
|
|
|
| 194 | 1 | Анализ контрольной работы. |
|
|
|
| 195 | 1 | Решение задач по теме «Многогранники» |
|
|
|
| 196 | 1 | Решение задач по теме «Многогранники» |
|
|
|
| 197 | 1 | Решение задач по теме «Многогранники» |
|
|
|
| 198 | 1 | Решение тестовых заданий. |
|
|
|
| 199 | 1 | Решение тестовых заданий. |
|
|
|
| 200 | 1 | Решение тестовых заданий. |
|
|
|
| 201 | 1 | Диагностическая работа в формате ЕГЭ |
|
|
|
| 202 | 1 | Диагностическая работа в формате ЕГЭ |
|
|
|
| 203 | 1 | Диагностическая работа в формате ЕГЭ |
|
|
|
| 204 | 1 | Диагностическая работа в формате ЕГЭ |
|
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике (профильный уровень 10 класс) (0.53 MB)
Рабочая программа по математике (профильный уровень 10 класс) (0.53 MB)
 0
0 4333
4333 572
572 Нравится
0
Нравится
0



