- Программы. Алгебра и начала математического анализа. 10 – 11 классы/авт.-сост. И.И.Зубарева, А.Г. Мордкович. – М: Мнемозина, 2011
- Программы общеобразовательных учреждений. Геометрия. 10 - 11 классы/ сост. Т. А. Бурмистрова, -М: Просвещение, 2010.
Рабочая программа по математике для 11-го класса составлена в соответствии со следующими нормативно-правовыми инструктивно-методическими документами:
В профильном курсе содержание образования, представленное в основной школе, развивается в следующих направлениях:
систематизация сведений о числах; формирование представлений о расширении числовых множеств от натуральных до комплексных как способе построения нового математического аппарата для решения задач окружающего мира и внутренних задач математики; совершенствование техники вычислений;
развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств, систем;
расширение и систематизация сведений о функциях, совершенствование графических умений; знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи;
расширение системы сведений о свойствах плоских фигур, систематическое изучение свойств пространственных тел, развитие представлений о геометрических измерениях;
развитие представлений о вероятностно-статистических закономерностях в окружающем мире;
совершенствование математического развития до уровня, позволяющего свободно применять изученные факты и методы при решении задач из различных разделов курса, а также использовать их в нестандартных ситуациях;
формирование способности строить и исследовать простейшие математические модели при решении прикладных задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
Рабочая программа разработана на основе федерального базисного учебного плана для образовательных учреждений РФ, в соответствии с которым на изучение курса математики в 11 классе выделено 204 часа (6 часов в неделю).
В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
Арифметические операции над многочленами от одной переменной. Деление многочлена на многочлен. Разложение многочлена на множители Арифметические операции над многочленами от одной переменной. Деление многочлена на многочлен. Разложение многочлена на множители Способы решения уравнений степени выше второй.
- раскладывать многочлены на множители.
Понятие корня n-ой степени из действительного числа. Функции 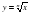 , их свойства и графики. Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы. Понятие степени с любым рациональным показателем. Степенные функции, их свойства и графики.
, их свойства и графики. Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы. Понятие степени с любым рациональным показателем. Степенные функции, их свойства и графики.
Определение показательной функции. Свойства показательной функции в зависимости от основания. Решение показательных уравнений и неравенств, используя график. Методы решения показательных уравнений. Способы решения показательных неравенств. Определение логарифма. Нахождение значений логарифмов по определению.
Определение логарифмической функции. Зависимость свойств логарифмической функции от основания логарифма. Построение графиков логарифмической функции, решение логарифмических уравнений и неравенств с помощью графиков. Производная показательной функции. Число e. Производная логарифмической функции. Степенная функция
- формулы производных показательной и логарифмической функций.
- формулы производных показательной и логарифмической функций, степенной функции.
- строить графики логарифмической и показательной функций, выполнять преобразования графиков;
- описывать по графику и формуле свойства логарифмической и показательной функций;
- решать уравнения и неравенства, используя свойства показательных и логарифмических функции и их графическое представление;
- решать показательные и логарифмические уравнения и неравенства и их системы.
- вычислять производные показательной и логарифмической функций, степенной функции.
-проводить преобразования числовых и буквенных выражений, содержащих степени; - строить графики степенных функций, выполнять преобразования графиков;
Первообразная. Первообразные степенных функций с целым показателем (n -1), тригонометрических функций. Простейшие правила нахождения первообразных.
-1), тригонометрических функций. Простейшие правила нахождения первообразных.
Площадь криволинейной трапеции. Формула Ньютона-Лейбница. Неопределенный интеграл. Понятие определенного интеграла. Применение интеграла в геометрии. Применение интеграла в физике.
- определение криволинейной трапеции.
- вычислять первообразные элементарных функций, применяя правила вычисления первообразных;
- вычислять площадь криволинейной трапеции.
Правило умножения. Комбинаторные задачи. Перестановки и факториалы. Выбор нескольких элементов. Биноминальные коэффициенты. Случайные события и их вероятности. Вероятность и геометрия. Независимые повторения испытаний с двумя исходами. Статистические методы обработки информации. Гауссова кривая. Закон больших чисел.
- комбинаторные принципы сложения и умножения.
-решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
-вычислять, в простейших случаях, вероятности событий на основе подсчета числа исходов.
-анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.
Равносильность уравнений. Общие методы решения уравнений. Равносильность неравенств. Уравнения и неравенства с модулем. Уравнения и неравенства со знаком радикала. Доказательство неравенств. Уравнения и неравенства с двумя переменными. Системы уравнений.
- понятия системы и совокупности неравенств.
-решать уравнения, неравенства и системы с применением графических представлений и свойств функций;
- изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
Преобразование тригонометрических, логарифмических, выражений, выражений, содержащих степень. Решение всех видов уравнений, неравенств, систем уравнений и неравенств. Производная. Функции и графики.
Уметь использовать приобретенные знания и умения в практической деятельности для решения задач разного уровня сложности на основе изученного материала.
Прямоугольная система координат в пространстве. Координаты вектора. Связь между координатами вектора и координатами точек. Простейшие задачи в координатах. Угол между векторами. Скалярное произведение векторов. Вычисление углов между прямыми и плоскостями. Центральная симметрия. Осевая симметрия. Зеркальная симметрия. Параллельный перенос.
-алгоритмы: разложения векторов по координатным векторам; сложения двух и более векторов; произведения вектора на число; разности двух векторов;
- формулы: координат середины отрезка; длины вектора; расстояния между двумя точками;
- формулу нахождения скалярного произведения векторов.
Иметь представление: об угле между векторами, скалярном квадрате вектора; о каждом из видов движения.
- применять формулы: координат середины отрезка; длины вектора; расстояния между двумя точками для решения задач координатно-векторным способом;
- уметь выполнять построение фигуры, симметричной относительно оси симметрии, центра симметрии, плоскости, при параллельном переносе.
Понятие цилиндра. Площадь поверхности цилиндра. Понятие конуса. Площадь поверхности конуса. Усеченный конус. Сфера и шар. Уравнение сферы. Взаимное расположение сферы и плоскости. Касательная плоскость к сфере. Площадь сферы.
-формулу площади сферы.
- уметь решать типовые задачи на нахождение площади сферы.
Понятие объема. Объем прямоугольного параллелепипеда. Объем прямой призмы. Объем цилиндра. Вычисление объемов тел с помощью определенного интеграла. Объем наклонной призмы. Объем пирамиды. Объем конуса
Объем шара. Объем шарового сегмента, шарового слоя и шарового сектора. Площадь сферы.
- формулы объемов прямоугольного параллелепипеда, прямой и наклонной призм, цилиндра, конуса, шара;
- формулу площади сферы.
Иметь представление шаровом сегменте, шаровом секторе, слое.
- решать задачи на вычисление площади сферы.
Треугольники. Четырехугольники. Окружность. Многогранники. Тела вращения.
Уметь использовать приобретенные знания и умения в практической деятельности для решения задач на основе изученных формул и свойств фигур.
1. Алгебра и начала математического анализа, 11 класс. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (профильный уровень)/ А.Г. Мордкович, П.В. Семенов. – М.: Мнемозина, 2012 ;
2. Алгебра и начала математического анализа, 11 класс. В 2 ч. Ч.2. Задачник для учащихся общеобразовательных учреждений (профильный уровень)/ А.Г. Мордкович и др. – М.: Мнемозина, 2012 ;
3. Геометрия. 10-11 классы : учеб. для общеобразовательных учреждений: базовый и профил. уровни/ Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.. – М.: Просвещение, 2012 г.
4. Программы. Алгебра и начала математического анализа. 10 – 11 классы/авт.-сост. И.И.Зубарева, А.Г. Мордкович. – М: Мнемозина, 2011
5. Программы общеобразовательных учреждений. Геометрия. 10 - 11 классы/ сост. Т. А. Бурмистрова, -М: Просвещение, 2010.
6. Алгебра и начала математического анализа. Контрольные работы.11 класс профильный уровень / В.И.Глизбург под редакцией. Г.Мордковича.– М.: Мнемозина, 2009.
7. Алгебра и начала математического анализа. Самостоятельные работы.11 класс / Л.А.Александрова под редакцией А.Г.Мордковича.– М.: Мнемозина, 2008.
8. С.М. Саакян, В.Ф. Бутузов. Изучение геометрии в 10 – 11 классах: Методические рекомендации к учебнику. Книга для учителя. – М.: Просвещение, 2008.
9. В.А. Яровенко. Поурочное разработки по геометрии. 11 класс. Дифференцированный подход. М.:ВАКО, 2006
10. Рабинович Е.М. Задачи и упражнения на готовых чертежах. 10- 11 классы. Геометрия. Москва – Харьков, издательство «Илекса» « Гимназия», 2006
11. Ковалёва Г.И. Дидактический материал по геометрии для 10 – 11 классов. Разрезные карточки по стереометрии. – Волгоград: Учитель, 2006
12. А.В. Фарков . Математические олимпиады в школе. 5 – 11 классы. Москва, издательство «Айрис - пресс», 2005
13. Контрольно-измерительные материалы. Алгебра и начала анализа: 11 класс/Сост. А.А. Рурукин.- М: ВАКО, 2011
14. Авторские презентации к урокам.
15. СD Виртуальная школа Кирилла и Мефодия, «Алгебра 10 -11 классы».
16. Интернет-ресурс «Единая коллекция цифровых образовательных ресурсов». – http://school-collection.edu.ru.
17. Интернет-ресурс «Открытый банк заданий по математике». – http://mathege.ru:8080/or/ege/Main.
|
№ урока |
Тема урока |
Кол-во часов |
Тип урока |
Элементы содержания |
Требования к уровню подготовки обучающихся |
Вид контроля |
Дата проведения |
| план | факт. |
|
БЛОК 1. Повторение материала 10 класса (4 ч). Многочлены (10 ч). Степени и корни. Степенные функции (24 ч)
|
| 1 | Повторение. Формулы тригонометрии | 1 | КУ | Формулы половинного угла, формулы понижения степени | Знать основные формулы тригонометрии. Уметь применять формулы для упрощения выражений | УС, ФО |
|
|
| 2 | Повторение. Формулы тригонометрии | 1 | КУ | Вспомогательный аргумент, преобразование выражений Asinx + Bcоsx к виду Csin(x + t) | Знать основные формулы тригонометрии. Уметь применять формулы для упрощения выражений | УС, ФО |
|
|
| 3 | Повторение. Решение тригонометрических уравнений | 1 | КУ | Метод разложения на множители, однородные тригонометрические уравнения первой и второй степени, алгоритм решения уравнения | Уметь преобразовывать простые тригонометрические выражения; решать простые тригонометрические уравнения; решать тригонометрические уравнения. | УС, ФО |
|
|
| 4 | Повторение. Производная и ее применения. | 1 | КУ | Определение производной, алгоритм отыскания производной. Формулы дифференцирования. Правила дифференцирования. Уравнение касательной. Применение производной. | Уметь находить производные суммы, разности, произведения, частного; производные основных элементарных функций; исследовать в простейших случаях функции на монотонность функций, строить графики функций. Знать формулы нахождения производной | УС, СР |
|
|
| 5 | Многочлены от одной переменной. | 1 | УИНМ | Стандартный вид многочлена; приведенные и неприведенные многочлены; деление с остатком; теорема Безу: разложение многочлена на множители | Уметь выполнять арифметические операции над многочленами от одной переменной, делить многочлен на многочлен с остатком, раскладывать многочлены на множители. | УС |
|
|
| 6 | Многочлены от одной переменной. | 1 | УЗИ | Стандартный вид многочлена; приведенные и неприведенные многочлены; деление с остатком; теорема Безу: разложение многочлена на множители | Уметь выполнять арифметические операции над многочленами от одной переменной, делить многочлен на многочлен с остатком, раскладывать многочлены на множители. | УС, ФО |
|
|
| 7 | Многочлены от одной переменной. | 1 | УЗИ | Стандартный вид многочлена; приведенные и неприведенные многочлены; деление с остатком; теорема Безу: разложение многочлена на множители | Уметь выполнять арифметические операции над многочленами от одной переменной, делить многочлен на многочлен с остатком, раскладывать многочлены на множители. | УС, СР |
|
|
| 8 | Многочлены от нескольких переменных | 1 | КУ | Однородные и симметрические многочлены; симметрическая система уравнений | Уметь различать однородные, симметрические многочлены от нескольких переменных и их системы. Знать способы их решения.. | УС |
|
|
| 9 | Срезовая контрольная работа | 1 | КОЗ | Проверка знаний, умений и навыков учащихся по курсу математики за 10 класс | Учащихся демонстрируют умение обобщения и систематизации знаний по основным темам курса математики 10 класса. | КР |
|
|
| 10 | Многочлены от нескольких переменных | 1 | УЗИ | Однородные и симметрические многочлены; симметрическая система уравнений | Уметь различать однородные, симметрические многочлены от нескольких переменных и их системы. Знать способы их решения. Уметь решать различными способами задания с однородными и симметрическими многочленами от нескольких переменных. | УС, ФО |
|
|
| 11 | Уравнения высших степеней. | 1 | УИНМ | Решение уравнений методом разложения на множители и методом введения новой переменной | Знать методы решения уравнений высших степеней: метод разложения на множители и метод введения новой переменной. Уметь применять различные функционально – графические приемы возвратных уравнений. |
|
|
|
| 12 | Уравнения высших степеней. | 1 | УЗИ | Решение уравнений методом разложения на множители и методом введения новой переменной | Знать методы решения уравнений высших степеней: метод разложения на множители и метод введения новой переменной. Уметь применять различные функционально – графические приемы возвратных уравнений. | УС, СР |
|
|
| 13 | Уравнения высших степеней. | 1 | УПКЗУ | Решение уравнений методом разложения на множители и методом введения новой переменной | Знать методы решения уравнений высших степеней: метод разложения на множители и метод введения новой переменной. Уметь применять различные функционально – графические приемы возвратных уравнений. | УС, ФО |
|
|
| 14 | Контрольная работа №1 по теме «Многочлены» | 1 | КОЗ | Проверка знаний, умений и навыков учащихся по теме Многочлены» | Знать теоретический материал, изученный на предыдущих уроках. Уметь применять полученные знания, умения и навыки на практике | КР |
|
|
| 15 | Понятие корня n-ой степени из действительного числа. | 1 | УИНМ | Показатель корня; подкоренное число; корень нечетной степени из отрицательного числа | Знать определение корня n-ой степени, его свойства. Уметь выполнять преобразования выражений, содержащих радикалы, содержащие корни n-ой степени. | УС |
|
|
| 16 | Понятие корня n-ой степени из действительного числа. | 1 | УЗИ | Показатель корня; подкоренное число; корень нечетной степени из отрицательного числа | Знать определение корня n-ой степени, его свойства. Уметь выполнять преобразования выражений, содержащих радикалы, содержащие корни n-ой степени.
| УС, СР |
|
|
| 17 | Функции 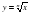 , их свойства и графики. , их свойства и графики. | 1 | УИНМ | Функции 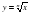 , их свойства и графики; область определения функции. , их свойства и графики; область определения функции. | Знать, как определять значение функции по значению аргумента при различных способах задания функции; строить график функции. Уметь применять свойства функций; исследовать функцию по схеме, при построении графиков использовать правила преобразования графиков.
| УС |
|
|
| 18 | Функции 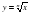 , их свойства и графики. , их свойства и графики. | 1 | УЗИ | Функции 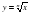 , их свойства и графики; область определения функции. , их свойства и графики; область определения функции. | Знать, как определять значение функции по значению аргумента при различных способах задания функции; строить график функции. Уметь применять свойства функций; исследовать функцию по схеме, при построении графиков использовать правила преобразования графиков.
| УС, ФО |
|
|
| 19 | Функции 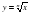 , их свойства и графики. , их свойства и графики. | 1 | УПЗУ | Функции 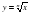 , их свойства и графики; область определения функции. , их свойства и графики; область определения функции. | Знать, как определять значение функции по значению аргумента при различных способах задания функции; строить график функции. Уметь применять свойства функций; исследовать функцию по схеме, при построении графиков использовать правила преобразования графиков.
| УС, СР |
|
|
| 20 | Свойства корня n-ой степени. | 1 | УИНМ | Теоремы о свойствах для неотрицательных значений переменных, содержащихся под знаком корней. | Знать свойства корня n-й степени, преобразовывать выражения, содержащие радикалы. Уметь применять свойства корня n-й степени; преобразовывать выражения, содержащие радикалы.
| УС |
|
|
| 21 | Свойства корня n-ой степени. | 1 | УЗИ | Теоремы о свойствах для неотрицательных значений переменных, содержащихся под знаком корней. | Знать свойства корня n-й степени, преобразовывать выражения, содержащие радикалы. Уметь применять свойства корня n-й степени; преобразовывать выражения, содержащие радикалы.
| УС, ФО |
|
|
| 22 | Свойства корня n-ой степени. | 1 | УПЗУ | Теоремы о свойствах для неотрицательных значений переменных, содержащихся под знаком корней. | Знать свойства корня n-й степени, преобразовывать выражения, содержащие радикалы. Уметь применять свойства корня n-й степени; преобразовывать выражения, содержащие радикалы.
| УС, СР |
|
|
| 23 | Преобразование выражений, содержащих радикалы. | 1 | УИНМ | Иррациональные выражения; вынесение множителя за знак радикала; внесение множителя под знак радикала | Знать, как выполнять арифметические действия, сочетая устные и письменные приемы; как находить значения корня натуральной степени по известным формулам и правилам преобразования буквенных выражений, включающих радикалы. Уметь выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени по известным формулам и правилам преобразования буквенных выражений, включающих радикалы
| УС |
|
|
| 24 | Преобразование выражений, содержащих радикалы. | 1 | УЗИ | Иррациональные выражения; вынесение множителя за знак радикала; внесение множителя под знак радикала | Знать, как выполнять арифметические действия, сочетая устные и письменные приемы; как находить значения корня натуральной степени по известным формулам и правилам преобразования буквенных выражений, включающих радикалы. Уметь выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени по известным формулам и правилам преобразования буквенных выражений
| УС, ФО |
|
|
| 25 | Преобразование выражений, содержащих радикалы.
| 1 | УПЗУ | Иррациональные выражения; вынесение множителя за знак радикала; внесение множителя под знак радикала | Знать, как выполнять арифметические действия, сочетая устные и письменные приемы; как находить значения корня натуральной степени по известным формулам и правилам преобразования буквенных выражений, включающих радикалы. Уметь выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени по известным формулам и правилам преобразования буквенных выражений, включающих радикалы | УС, СР |
|
|
| 26 | Преобразование выражений, содержащих радикалы. | 1 | УПКЗУ | УС, ФО |
|
|
| 27 | Контрольная работа № 2 по теме «Степени и корни»
| 1 | КОЗ | Показатель корня; подкоренное число; корень нечетной степени из отрицательного числа; иррациональные выражения; вынесение множителя за знак радикала; внесение множителя под знак радикала; функции 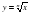 , их свойства и графики. , их свойства и графики. | Знать теоретический материал, изученный на предыдущих уроках. Уметь применять полученные знания, умения и навыки на практике | КР |
|
|
| 28 | Контрольная работа № 2 по теме «Степени и корни» | 1 | КОЗ | КР |
|
|
| 29 | Понятие степени с любым рациональным показателем.
| 1 | УИНМ |
Целочисленные показатели степени; степень с дробным показателем; свойства степеней. | Знать, как находить значения степени с рациональным показателем; проводить по известным формулам и правилам преобразования буквенных выражений. Уметь обобщать понятие о показателе степени, выполняя преобразование выражений, содержащих радикалы; обосновывать суждения, давать определения, приводить доказательства, примеры включающих степени. | УС |
|
|
| 30 | Понятие степени с любым рациональным показателем. | 1 | КУ | УС, ФО |
|
|
| 31 | Понятие степени с любым рациональным показателем. | 1 | УЗИ | Целочисленные показатели степени; степень с дробным показателем; свойства степеней. | Знать, как находить значения степени с рациональным показателем; проводить по известным формулам и правилам преобразования буквенных выражений. Уметь обобщать понятие о показателе степени, выполняя преобразование выражений, содержащих радикалы; обосновывать суждения, давать определения, приводить доказательства, примеры включающих степени. | УС, СР |
|
|
| 32
| Степенные функции, их свойства и графики | 1 | УИНМ | Степенные функции типа y = xr , их свойства и графики. Построение графиков. Исследование функций. Формула производной степенной функции | Знать понятие степенных функций при различных значениях показателя. Уметь строить графики степенных функций при различных значениях показателя; описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения | УС |
|
|
| 33 | Степенные функции, их свойства и графики | 1 | КУ | Степенные функции типа y = xr , их свойства и графики. Построение графиков. Исследование функций. Формула производной степенной функции | Знать понятие степенных функций при различных значениях показателя. Уметь строить графики степенных функций при различных значениях показателя; описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения | УС, ФО |
|
|
| 34 | Степенные функции, их свойства и графики | 1 | УЗИ | Степенные функции типа y = xr , их свойства и графики. Построение графиков. Исследование функций. Формула производной степенной функции | Знать понятие степенных функций при различных значениях показателя. Уметь строить графики степенных функций при различных значениях показателя; описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения | УС, ФО |
|
|
| 35 | Степенные функции, их свойства и графики | 1 | УЗИ | Степенные функции типа y = xr , их свойства и графики. Построение графиков. Исследование функций. Формула производной степенной функции | Знать понятие степенных функций при различных значениях показателя. Уметь строить графики степенных функций при различных значениях показателя; описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения
| УС, СР |
|
|
| 36 | Извлечение корней из комплексных чисел | 1 | УПЗУ | Комплексные числа, извлечение корней из комплексных чисел | Знать, как выполнять арифметические действия над комплексными числами в разных формах записи. Уметь привести примеры, подобрать аргументы, сформулировать выводы.
| УС |
|
|
| 37 | Извлечение корней из комплексных чисел | 1 | УПКЗУ | Комплексные числа, извлечение корней из комплексных чисел | Знать, как выполнять арифметические действия над комплексными числами в разных формах записи. Уметь привести примеры, подобрать аргументы, сформулировать выводы. | УС, ФО |
|
|
| 38 | Контрольная работа № 3 по теме «Степенные функции» | 1 | КОЗ | Целочисленные показатели степени; степень с дробным показателем; свойства степеней. Степенные функции типа y = xr , их свойства и графики. Построение графиков. Исследование функций. Формула производной степенной функции | Знать теоретический материал, изученный на предыдущих уроках. Уметь применять полученные знания, умения и навыки на практике | КР |
|
|
|
БЛОК 2. Метод координат в пространстве. Движения (18 ч)
|
| 39 | Прямоугольная система координат в пространстве. | 1 | УИНМ | Координатные плоскости; координаты точки (абсцисса, ордината, аппликата) | Знать: составляющие прямоугольной системы координат в пространстве. Уметь: строить точку по координатам и определять координаты точки. | ФО |
|
|
| 40 | Координаты вектора. | 1 | УИНМ | Единичный вектор; координатные вектора; коэффициенты разложения вектора по координатным векторам; правила нахождения по координатам данных векторов координаты их суммы и разности.
| Знать: определение координат вектора Уметь: выполнять действия над векторами
| ФО |
|
|
| 41 | Координаты вектора.
| 1 | УПЗУ | Единичный вектор; координатные вектора; коэффициенты разложения вектора по координатным векторам; правила нахождения по координатам данных векторов координаты их суммы и разности. | Знать: определение координат вектора Уметь: выполнять действия над векторами
| ФО |
|
|
| 42 | Связь между координатами векторов и координатами точек. | 1 | УИНМ | Радиус-вектор; начало вектора; конец вектора. | Знать: о связи между координатами векторов и координатами точек Уметь: применять формулы для решения задач | ФО |
|
|
| 43 | Простейшие задачи в координатах.
| 1 | УИНМ | Координаты середины отрезка; длина вектора по его координатам; расстояние между двумя точками.
| Знать: о трех простейших задачах в координатах Уметь: решать простейшие задачи в координатах |
|
|
|
| 44 | Простейшие задачи в координатах.
| 1 | УПЗУ | Координаты середины отрезка; длина вектора по его координатам; расстояние между двумя точками. | Знать: о трех простейших задачах в координатах Уметь: решать задачи, используя эти простейшие задачи в координатах
| ФО |
|
|
| 45 | Простейшие задачи в координатах.
| 1 | К КУ | Координаты середины отрезка; длина вектора по его координатам; расстояние между двумя точками. | Знать: о трех простейших задачах в координатах Уметь: решать задачи, используя эти простейшие задачи в координатах
| СР |
|
|
| 46 | Контрольная работа № 4 по теме: «Координаты точки и координаты вектора»
| 1 | КОЗ | Координатные плоскости; координаты точки (абсцисса, ордината, аппликата); единичный вектор; коэффициенты разложения вектора по координатным векторам; радиус-вектор; координаты середины отрезка; длина вектора по его координатам; расстояние между двумя точками. | Знать: составляющие прямоугольной системы координат в пространстве; определение координат вектора; о связи между координатами векторов и координатами точек; о 3 простейших задачах в координатах. Уметь: строить точку по координатам и определять координаты точки; выполнять действия над векторами; решать простейшие задачи в координатах.
| КР |
|
|
| 47 | Угол между векторами. Скалярное произведение векторов | 1 | КУ | Угол между векторами; перпендикулярные векторы. | Знать: об угле между векторами Уметь: вычислять угол между векторами в пространстве | ФО |
|
|
| 48 | Скалярное произведение векторов.
| 1 | УИНМ | Скалярное произведение векторов; скалярный квадрат; длина вектора | Знать: определение скалярного произведения векторов Уметь: находить скалярное произведение векторов | ФО |
|
|
| 49 | Скалярное произведение векторов. | 1 | УПЗУ | Скалярное произведение векторов; скалярный квадрат; длина вектора | Знать: определение скалярного произведения векторов Уметь: находить скалярное произведение векторов | ФО |
|
|
| 50 | Вычисление углов между прямыми и плоскостями.
| 1 | УИНМ | Ненулевой вектор; направляющий вектор; угол между прямыми и плоскостями. | Знать: формулу для вычисления углов между прямыми и плоскостями в пространстве. Уметь: применять формулу для вычисления углов между прямыми и плоскостями в пространстве к решению несложных задач. | ФО |
|
|
| 51 | Решение задач.
| 1 | УПЗУ | Угол между векторами; скалярное произведение векторов; скалярный квадрат; длина вектора; направляющий вектор; угол между прямыми и плоскостями. | Знать: формулу для вычисления углов между прямыми и плоскостями в пространстве Уметь: применять формулу к решению задач. | ФО
|
|
|
| 52 | Центральная симметрия. Осевая симметрия. | 1 | КУ | Движения; отображение плоскости на себя; отображение пространства на себя; центральная симметрия; осевая симметрия. | Знать: различные виды симметрии; определение центральной и осевой симметрий. Уметь: решать простейшие задачи. | ФО |
|
|
| 53 | Зеркальная симметрия. Параллельный перенос. | 1 | УИНМ | Зеркальная симметрия; параллельный перенос | Знать: определение зеркальной симметрии и параллельного переноса. Уметь: решать простейшие задачи. | ФО |
|
|
| 54 | Решение задач.
| 1 | КУ | Движения; отображение плоскости на себя; отображение пространства на себя; центральная симметрия; осевая симметрия; зеркальная симметрия; параллельный перенос. | Знать: виды движений и их свойства Уметь: решать простейшие задачи.
| ФО |
|
|
| 55 | Решение задач.
| 1 | УПЗУ | Движения; отображение плоскости на себя; отображение пространства на себя; центральная симметрия; осевая симметрия; зеркальная симметрия; параллельный перенос. | Знать: виды движений и их свойства Уметь: решать простейшие задачи.
| ФО, Т |
|
|
| 56 | Контрольная работа № 5 по теме: «Скалярное произведение векторов»
| 1 | КОЗ | Угол между векторами; скалярное произведение векторов; скалярный квадрат; длина вектора; направляющий вектор; угол между прямыми и плоскостями; движения; отображение плоскости на себя; отображение пространства на себя; центральная симметрия; осевая симметрия; зеркальная симметрия; параллельный перенос | Знать: определение угла между векторами, скалярное произведение векторов, центральная, осевая, зеркальная симметрии, параллельный перенос Уметь: вычислять угол между прямыми и плоскостями и решать несложные задачи на движение. | КР |
|
|
|
БЛОК 3. Показательная и логарифмическая функции (31 ч)
|
| 57 | Показательная функция, ее свойства и график. | 1 | КУ | Показательная функция. График показательной функции; свойства показательной функции | Знать определение показательной функции. Уметь строить график показательной функции; находить область определения показательной функции | УС, ФО |
|
|
| 58 | Показательная функция, ее свойства и график. | 1 | УЗИ | Показательная функция. График показательной функции; свойства показательной функции | Знать определение показательной функции. Уметь строить график показательной функции; находить область определения показательной функции | УС, СР |
|
|
| 59 | Показательная функция, ее свойства и график. | 1 | УЗИ | Показательная функция. График показательной функции; свойства показательной функции | Знать определение показательной функции. Уметь строить график показательной функции; находить область определения показательной функции
| УС, СР |
|
|
| 60 | Показательные уравнения. | 1 | УИНМ | Показательные уравнения. Свойства показательных уравнений. Методы решения показательных уравнений. | Знать определение показательного уравнения. Уметь решать показательные уравнения, применяя комбинацию нескольких алгоритмов; изображать на координатной плоскости множества решений простейших уравнений, и их систем. | УС |
|
|
| 61 | Показательные уравнения. | 1 | КУ | Показательные уравнения. Свойства показательных уравнений. Методы решения показательных уравнений. | Знать определение показательного уравнения. Уметь решать показательные уравнения, применяя комбинацию нескольких алгоритмов; изображать на координатной плоскости множества решений простейших уравнений, и их систем. | УС, ФО |
|
|
| 62 | Показательные уравнения. | 1 | УЗИ | Показательные уравнения. Свойства показательных уравнений. Методы решения показательных уравнений. | Знать определение показательного уравнения. Уметь решать показательные уравнения, применяя комбинацию нескольких алгоритмов; изображать на координатной плоскости множества решений простейших уравнений, и их систем. | УС, СР |
|
|
| 63 | Показательные неравенства. | 1 |
| Показательные неравенства. Свойства показательных неравенств. | Знать определение показательного неравенства Уметь решать показательные неравенства, применяя комбинацию нескольких алгоритмов; изображать на координатной плоскости множества решений простейших неравенств и их систем. | УС |
|
|
| 64 | Показательные неравенства. | 1 | УПЗУ | Показательные неравенства. Свойства показательных неравенств. | Знать определение показательного неравенства Уметь решать показательные неравенства, применяя комбинацию нескольких алгоритмов; изображать на координатной плоскости множества решений простейших неравенств и их систем. | УС, СР |
|
|
| 65 | Понятие логарифма. | 1 | УИНМ | Логарифм положительного числа. Логарифмирование. Десятичный логарифм. | Знать понятие логарифма и некоторые его свойства. Уметь выполнять преобразования логарифмических выражений и вычислять логарифмы чисел. Могут собрать материал для сообщения по заданной теме. | УС, ФО |
|
|
| 66 | Понятие логарифма. | 1 | УПЗУ | Логарифм положительного числа. Логарифмирование. Десятичный логарифм. | Знать понятие логарифма и некоторые его свойства. Уметь выполнять преобразования логарифмических выражений и вычислять логарифмы чисел. Могут собрать материал для сообщения по заданной теме.
| УС, ФО |
|
|
| 67 | Логарифмическая функция, ее свойства и график. | 1 | УИНМ | Логарифмическая функция, свойства функции и ее график. Логарифмическая кривая. | Знать определение логарифмической функции, ее свойства в зависимости от основания. Уметь определять значение функции по значению аргумента при различных способах задания функции; применять свойства логарифмической функции; владеть приёмами построения и исследования математических моделей.
| УС |
|
|
| 68 | Логарифмическая функция, ее свойства и график. | 1 | КУ | Логарифмическая функция, свойства функции и ее график. Логарифмическая кривая. | Знать определение логарифмической функции, ее свойства в зависимости от основания. Уметь определять значение функции по значению аргумента при различных способах задания функции; применять свойства логарифмической функции; владеть приёмами построения и исследования математических моделей. | УС, СР |
|
|
| 69 | Логарифмическая функция, ее свойства и график. | 1 | УПКЗУ | Логарифмическая функция, свойства функции и ее график. Логарифмическая кривая. | Знать определение логарифмической функции, ее свойства в зависимости от основания. Уметь определять значение функции по значению аргумента при различных способах задания функции; применять свойства логарифмической функции; владеть приёмами построения и исследования математических моделей. | УС, ФО |
|
|
| 70 | Контрольная работа № 6 по теме «Показательная и логарифмическая функции» | 1 | КОЗ | Степень с иррациональным показателем. Показательная функция. Свойства и график показательной функции. Экспонента. Показательные уравнения и неравенства. Логарифм. Логарифмирование. Десятичный логарифм. Логарифмическая функция, свойства функции и ее график.
| Знать теоретический материал, изученный на предыдущих уроках. Уметь применять полученные знания, умения и навыки на практике | КР |
|
|
| 71 | Контрольная работа № 6 по теме «Показательная и логарифмическая функции» | 1 | КОЗ | Степень с иррациональным показателем. Показательная функция. Свойства и график показательной функции. Экспонента. Показательные уравнения и неравенства. Логарифм. Логарифмирование. Десятичный логарифм. Логарифмическая функция, свойства функции и ее график.
| Знать теоретический материал, изученный на предыдущих уроках. Уметь применять полученные знания, умения и навыки на практике | КР |
|
|
| 72 | Свойства логарифмов. | 1 | УИНМ | Свойства логарифмов. Логарифмирование. Потенцирование. Свойства десятичного логарифма. Формула перехода к новому основанию логарифма. | Знать свойства логарифмов; формулу перехода к новому основанию и два частных случая формулы перехода к новому основанию логарифма. Уметь применять свойства логарифмов; формулу перехода к новому основанию. Уметь обосновывать суждения, давать определения, приводить доказательства, примеры.
| УС |
|
|
| 73 | Свойства логарифмов. | 1 | КУ | Свойства логарифмов. Логарифмирование. Потенцирование. Свойства десятичного логарифма. Формула перехода к новому основанию логарифма. | Знать свойства логарифмов; формулу перехода к новому основанию и два частных случая формулы перехода к новому основанию логарифма. Уметь применять свойства логарифмов; формулу перехода к новому основанию. Уметь обосновывать суждения, давать определения, приводить доказательства, примеры.
| УС, ФО |
|
|
| 74 | Свойства логарифмов. | 1 | УЗИ | Свойства логарифмов. Логарифмирование. Потенцирование. Свойства десятичного логарифма. Формула перехода к новому основанию логарифма. | Знать свойства логарифмов; формулу перехода к новому основанию и два частных случая формулы перехода к новому основанию логарифма. Уметь применять свойства логарифмов; формулу перехода к новому основанию. Уметь обосновывать суждения, давать определения, приводить доказательства, примеры.
| УС, ФО |
|
|
| 75 | Свойства логарифмов. | 1 | УПЗУ | Свойства логарифмов. Логарифмирование. Потенцирование. Свойства десятичного логарифма. Формула перехода к новому основанию логарифма. | Знать свойства логарифмов; формулу перехода к новому основанию и два частных случая формулы перехода к новому основанию логарифма. Уметь применять свойства логарифмов; формулу перехода к новому основанию. Уметь обосновывать суждения, давать определения, приводить доказательства, примеры. | СР |
|
|
| 76 | Логарифмические уравнения. | 1 | УИНМ | Логарифмические уравнения. Теорема о логарифмическом уравнении. Потенцирование. Методы решения логарифмических уравнений. | Знать понятие логарифмического уравнения; теорему о логарифмическом уравнении; методы решения логарифмических уравнений. Уметь решать простейшие логарифмические уравнения по определению. | УС |
|
|
| 77 | Логарифмические уравнения. | 1 | КУ | Логарифмические уравнения. Теорема о логарифмическом уравнении. Потенцирование. Методы решения логарифмических уравнений. | Знать понятие логарифмического уравнения; теорему о логарифмическом уравнении; методы решения логарифмических уравнений. Уметь решать простейшие логарифмические уравнения по определению. | УС, ФО |
|
|
| 78 | Логарифмические уравнения. | 1 | УЗИ | Логарифмические уравнения. Теорема о логарифмическом уравнении. Потенцирование. Методы решения логарифмических уравнений. | Знать понятие логарифмического уравнения; теорему о логарифмическом уравнении; методы решения логарифмических уравнений. Уметь решать простейшие логарифмические уравнения по определению.
| УС, ФО |
|
|
| 79 | Логарифмические уравнения. | 1 | УПЗУ | Логарифмические уравнения. Теорема о логарифмическом уравнении. Потенцирование. Методы решения логарифмических уравнений. | Знать понятие логарифмического уравнения; теорему о логарифмическом уравнении; методы решения логарифмических уравнений. Уметь решать простейшие логарифмические уравнения по определению. | УС, СР |
|
|
| 80 | Логарифмические неравенства. | 1 | УИНМ | Логарифмические неравенства. Теорема о логарифмическом неравенстве. Метод интервалов. | Знать алгоритм решения логарифмического неравенства в зависимости от основания. Уметь решать простейшие логарифмические неравенства, применяя метод замены переменных для сведении логарифмического неравенства к рациональному виду. | УС |
|
|
| 81 | Логарифмические неравенства. | 1 | КУ | Логарифмические неравенства. Теорема о логарифмическом неравенстве. Метод интервалов. | Знать алгоритм решения логарифмического неравенства в зависимости от основания. Уметь решать простейшие логарифмические неравенства, применяя метод замены переменных для сведении логарифмического неравенства к рациональному виду. | УС, ФО |
|
|
| 81 | Логарифмические неравенства. | 1 | УЗИ | Логарифмические неравенства. Теорема о логарифмическом неравенстве. Метод интервалов. | Знать алгоритм решения логарифмического неравенства в зависимости от основания. Уметь решать простейшие логарифмические неравенства, применяя метод замены переменных для сведении логарифмического неравенства к рациональному виду. | УС, СР |
|
|
| 83 | Дифференцирование показательной и логарифмической функций | 1 | УИНМ | Число е. График функции y = ex и ее свойства. Натуральные логарифмы. Функция y = lnx, ее свойства, график, дифференцирование. | Знать формулы для нахождения производной и первообразной показательной и логарифмической функций. Уметь вычислять производные и первообразные простейших показательных и логарифмических функций; решать практические задачи с помощью аппарата дифференциального и интегрального исчисления.
| УС |
|
|
| 84 | Дифференцирование показательной и логарифмической функций | 1 | КУ | Число е. График функции y = ex и ее свойства. Натуральные логарифмы. Функция y = lnx, ее свойства, график, дифференцирование. | Знать формулы для нахождения производной и первообразной показательной и логарифмической функций. Уметь вычислять производные и первообразные простейших показательных и логарифмических функций; решать практические задачи с помощью аппарата дифференциального и интегрального исчисления.
| УС, СР |
|
|
| 85 | Дифференцирование показательной и логарифмической функций | 1 | УПКЗУ | Число е. График функции y = ex и ее свойства. Натуральные логарифмы. Функция y = lnx, ее свойства, график, дифференцирование. | Знать формулы для нахождения производной и первообразной показательной и логарифмической функций. Уметь вычислять производные и первообразные простейших показательных и логарифмических функций; решать практические задачи с помощью аппарата дифференциального и интегрального исчисления. | УС, ФО |
|
|
| 86 | Контрольная работа № 7 по теме «Логарифмические у равнения и неравенства» | 1 | КОЗ | Свойства логарифмов. Логарифмирование. Потенцирование. Свойства десятичного логарифма. Формула перехода к новому основанию логарифма. Логарифмические уравнения и неравенства. Число е. График функции y = ex и ее свойства. Натуральные логарифмы. Функция y = lnx, ее свойства, график, дифференцирование | Знать теоретический материал, изученный на предыдущих уроках. Уметь применять полученные знания, умения и навыки на практике | КР |
|
|
| 87 | Контрольная работа № 7 по теме «Логарифмические у равнения и неравенства» | 1 | КОЗ | Свойства логарифмов. Логарифмирование. Потенцирование. Свойства десятичного логарифма. Формула перехода к новому основанию логарифма. Логарифмические уравнения и неравенства. Число е. График функции y = ex и ее свойства. Натуральные логарифмы. Функция y = lnx, ее свойства, график, дифференцирование
| Знать теоретический материал, изученный на предыдущих уроках. Уметь применять полученные знания, умения и навыки на практике | КР |
|
|
|
БЛОК 4. Цилиндр, конус и шар (20 ч)
|
| 88 | Понятие цилиндра.
| 1 | КУ | Цилиндрическая поверхность; боковая поверхность цилиндра; образующие цилиндра; основание, ось, высота, радиус, сечения цилиндра. | Знать: определение цилиндра. Уметь: строить чертеж цилиндра, секущие плоскости цилиндра | ФО |
|
|
| 89 | Площадь поверхности цилиндра.
| 1 | УИНМ | Цилиндр; развертка боковой поверхности цилиндра; площадь боковой поверхности цилиндра | Знать: формулы площади полной поверхности цилиндра Уметь: применять формулы площади полной поверхности цилиндра к решению задач на вычисление. | ФО |
|
|
| 90 | Площадь поверхности цилиндра. | 1 | УПЗУ | Цилиндр; развертка боковой поверхности цилиндра; площадь боковой поверхности цилиндра | Знать: формулы площади полной поверхности цилиндра Уметь: применять формулы площади полной поверхности цилиндра к решению задач на вычисление и доказательство. | ФО |
|
|
| 91 | Понятие конуса. | 1 | УИНМ | Коническая поверхность; образующие конической поверхности; конус; элементы конуса (высота, образующие, вершина, ось); сечение конуса. | Знать: определение конуса. Уметь: изображать конус. | ФО |
|
|
| 92 | Площадь поверхности конуса.
| 1 | КУ | Развертка конуса; площадь боковой поверхности конуса; площадь полной поверхности конуса. | Знать: формулы для вычисления площади полной поверхности конуса. Уметь: применять формулы площади полной поверхности конуса к решению задач на вычисление. | ФО |
|
|
| 93 | Усечённый конус. | 1 | УИНМ | Секущая плоскость; усеченный конус; элементы усеченного конуса (основания, высота, образующие, боковая поверхн.) | Знать: определение полного и усеченного конусов. Уметь: изображать усеченный конус. | ФО |
|
|
| 94 | Решение задач.
| 1 | УПЗУ | Конус, усеченный конус; цилиндр; площадь поверхности конуса; площадь поверхности цилиндра. | Знать: формулы для вычисления боковой поверхности усеченного конуса Уметь: применять формулы полной поверхности конуса к решению задач | СР |
|
|
| 95 | Сфера и шар. Уравнение сферы.
| 1 | УИНМ | Сфера; шар; элементы сферы и шара (центр, радиус, диаметр); уравнение сферы. | Знать: определение сферы и шара, уравнение сферы. Уметь: применять формулы для решения простейших задач на составление уравнения сферы | ФО |
|
|
| 96 | Взаимное расположение сферы и плоскости.
| 1 | КУ | Три случая взаимного расположения сферы и плоскости. | Знать: определение взаимного расположения сферы и плоскости. Уметь: применять формулы для решения задач. | ФО |
|
|
| 97 | Касательная плоскость к сфере. | 1 | УИНМ | Касательная плоскость к сфере; точка касания; свойство касательной плоскости.
| Знать: определение касательной плоскости к сфере Уметь: применять формулы для решения задач. | ФО |
|
|
| 98 | Площадь сферы.
| 1 | КУ | Многогранник, описанный около сферы (шара); сфера, вписанная в многогранник; площадь сферы. | Знать: определение сферы и шара, площади сферы. Уметь: применять формулы для решения задач. | ФО |
|
|
| 99 | Решение задач на цилиндр.
| 1 | УПЗУ | Цилиндр, элементы цилиндра (основание, ось, высота, радиус); боковая поверхность цилиндра; площадь боковой поверхности цилиндра. | Знать: определение цилиндра; формулы площади полной поверхности цилиндра Уметь: выполнять чертежи по условиям задач и решать простейшие задачи. | ФО |
|
|
| 100 | Решение задач на конус.
| 1 | УПЗУ | Конус, усеченный конус; элементы конуса (высота, образующие, вершина, ось); сечение конуса; площадь поверхности конуса. | Знать: определение конуса; формулы для вычисления полной поверхности конуса. Уметь: выполнять чертежи по условиям задач и решать простейшие задачи.
| ФО |
|
|
| 101 | Решение задач на шар. | 1 | УПЗУ | Сфера; шар; элементы сферы и шара (центр, радиус, диаметр); уравнение сферы; площадь сферы.. | Знать: определение сферы и шара, уравнение сферы. Уметь: выполнять чертежи по условиям задач и решать простейшие задачи.
| СР |
|
|
| 102 | Решение задач.
| 1 | УПЗУ | Конус, цилиндр, шар, сфера, площадь поверхности конуса, цилиндра; площадь сферы; уравнение сферы; касательная плоскость к сфере; точка касания; свойство касательной плоскости; три случая взаимного расположения сферы и плоскости.
| Знать: основные многогранники. Уметь: изображать основные многогранники, выполнять чертежи по условиям задач и решать простейшие задачи. | ФО |
|
|
| 103 | Решение задач.
| 1 | УПЗУ | Конус, цилиндр, шар, сфера, площадь поверхности конуса, цилиндра; площадь сферы; уравнение сферы; касательная плоскость к сфере; точка касания; свойство касательной плоскости; три случая взаимного расположения сферы и плоскости.
| Знать: основные многогранники. Уметь: изображать многогранники, выполнять чертежи по условиям задач и решать простейшие задачи. | ФО |
|
|
| 104 | Решение задач на вписанные и описанные многогранники.
| 1 | КУ | Многогранник описанный около сферы; сфера вписанная в многогранник; многогранник вписанный в сферу; сфера описанная около многогранника.
| Знать: определение вписанных и описанных многогранников, изображать многогранники, Уметь: выполнять чертежи по условиям задач и решать простейшие задачи. | ФО |
|
|
| 105 | Решение задач на вписанные и описанные многогранники.
| 1 | КУ | Многогранник описанный около сферы; сфера вписанная в многогранник; многогранник вписанный в сферу; сфера описанная около многогранника.
| Знать: определение вписанных и описанных многогранников, изображать многогранники, Уметь: выполнять чертежи по условиям задач и решать простейшие задачи.
| ФО |
|
|
| 106 | Решение задач на вписанные и описанные многогранники.
| 1 | УПЗУ | Многогранник описанный около сферы; сфера вписанная в многогранник; многогранник вписанный в сферу; сфера описанная около многогранника. | Знать: основные многогранники Уметь: изображать многогранники, выполнять чертежи по условиям задач и решать простейшие задачи. | СР |
|
|
| 107 | Контрольная работа № 8 по теме: «Цилиндр, конус и шар» | 1 | КОЗ | Конус, цилиндр, шар, сфера, площадь поверхности конуса, цилиндра; площадь сферы; уравнение сферы; касательная плоскость к сфере; точка касания; свойство касательной плоскости; три случая взаимного расположения сферы и плоскости; вписанные в сферу и описанные около сферы многогранники
| Знать: понятия: цилиндр, площадь поверхности цилиндра Уметь: изображать многогранники, выполнять чертежи по условиям задач и решать простейшие задачи. | КР |
|
|
|
БЛОК 5. Первообразная и интеграл (9 ч). Элементы теории вероятностей и математической статистики (9 ч)
|
| 108 | Первообразная и неопределенный интеграл | 1 | УИНМ | Задача о восстановлении закона движения по известной скорости. Интегрирование. Определение первообразной и ее общий вид. Таблица формул для нахождения первообразных. Правила отыскания первообразных. Неопределенный интеграл. Таблица неопределенных интегралов. Правила интегрирования. | Знать определение первообразной и неопределенного интеграла, понятие интегрирование; таблицы формул для нахождения первообразных и основных неопределенных интегралов; правила отыскания первообразных. Уметь находить первообразные известных функций. | УС |
|
|
| 109 | Первообразная и неопределенный интеграл | 1 | КУ | Задача о восстановлении закона движения по известной скорости. Интегрирование. Определение первообразной и ее общий вид. Таблица формул для нахождения первообразных. Правила отыскания первообразных. Неопределенный интеграл. Таблица неопределенных интегралов. Правила интегрирования. | Знать определение первообразной и неопределенного интеграла, понятие интегрирование; таблицы формул для нахождения первообразных и основных неопределенных интегралов; правила отыскания первообразных. Уметь находить первообразные известных функций. | УС, ФО |
|
|
| 110 | Первообразная и неопределенный интеграл | 1 | УЗИ | Задача о восстановлении закона движения по известной скорости. Интегрирование. Определение первообразной и ее общий вид. Таблица формул для нахождения первообразных. Правила отыскания первообразных. Неопределенный интеграл. Таблица неопределенных интегралов. Правила интегрирования. | Знать определение первообразной и неопределенного интеграла, понятие интегрирование; таблицы формул для нахождения первообразных и основных неопределенных интегралов; правила отыскания первообразных. Уметь находить первообразные известных функций. | УС, СР |
|
|
| 111 | Определенный интеграл. | 1 | УИНМ | Вычисление площади криволинейной трапеции. Предел последовательности. Вычисление массы стержня. Физическая масса. Перемещение точки. Определенный интеграл. Геометрический и физический смысл определенного интеграла. Формула Ньютона-Лейбница. | Знать понятия криволинейной трапеции, определенный интеграл; происхождение слова интеграл; геометрический и физический смысл определенного интеграла; формулы для вычисления площади криволинейной трапеции, физический массы, перемещения точки; формулу Ньютона-Лейбница. Уметь вычислять площади фигур с помощью определенного интеграла; применять формулу Ньютона – Лейбница. | УС |
|
|
| 112 | Определенный интеграл. | 1 | УЗИ | Вычисление площади криволинейной трапеции. Предел последовательности. Вычисление массы стержня. Физическая масса. Перемещение точки. Определенный интеграл. Геометрический и физический смысл определенного интеграла. Формула Ньютона-Лейбница. | Знать понятия криволинейной трапеции, определенный интеграл; происхождение слова интеграл; геометрический и физический смысл определенного интеграла; формулы для вычисления площади криволинейной трапеции, физический массы, перемещения точки; формулу Ньютона-Лейбница. Уметь вычислять площади фигур с помощью определенного интеграла; применять формулу Ньютона – Лейбница. | УС, ФО |
|
|
| 113 | Определенный интеграл. | 1 | УЗИ | Вычисление площади криволинейной трапеции. Предел последовательности. Вычисление массы стержня. Физическая масса. Перемещение точки. Определенный интеграл. Геометрический и физический смысл определенного интеграла. Формула Ньютона-Лейбница. | Знать понятия криволинейной трапеции, определенный интеграл; происхождение слова интеграл; геометрический и физический смысл определенного интеграла; формулы для вычисления площади криволинейной трапеции, физический массы, перемещения точки; формулу Ньютона-Лейбница. Уметь вычислять площади фигур с помощью определенного интеграла; применять формулу Ньютона – Лейбница. | УС, ФО |
|
|
| 114 | Определенный интеграл. | 1 | УПЗУ | Вычисление площади криволинейной трапеции. Предел последовательности. Вычисление массы стержня. Физическая масса. Перемещение точки. Определенный интеграл. Геометрический и физический смысл определенного интеграла. Формула Ньютона-Лейбница. | Знать понятия криволинейной трапеции, определенный интеграл; происхождение слова интеграл; геометрический и физический смысл определенного интеграла; формулы для вычисления площади криволинейной трапеции, физический массы, перемещения точки; формулу Ньютона-Лейбница. Уметь вычислять площади фигур с помощью определенного интеграла; применять формулу Ньютона – Лейбница. | УС, СР |
|
|
| 115 | Определенный интеграл. | 1 | УПКЗУ | Вычисление площади криволинейной трапеции. Предел последовательности. Вычисление массы стержня. Физическая масса. Перемещение точки. Определенный интеграл. Геометрический и физический смысл определенного интеграла. Формула Ньютона-Лейбница. | Знать понятия криволинейной трапеции, определенный интеграл; происхождение слова интеграл; геометрический и физический смысл определенного интеграла; формулы для вычисления площади криволинейной трапеции, физический массы, перемещения точки; формулу Ньютона-Лейбница. Уметь вычислять площади фигур с помощью определенного интеграла; применять формулу Ньютона – Лейбница. | УС, ФО |
|
|
| 116 | Контрольная работа № 9 по теме «Первообразная и интеграл» | 1 | КОЗ | Вычисление площади криволинейной трапеции. Предел последовательности. Вычисление массы стержня. Физическая масса. Перемещение точки. Определенный интеграл. Геометрический и физический смысл определенного интеграла. Формула Ньютона-Лейбница. | Знать теоретический материал, изученный на предыдущих уроках. Уметь применять полученные знания, умения и навыки на практике. | КР |
|
|
| 117 | Вероятность и геометрия | 1 | УИНМ | Классическая вероятностная схема. Классическое определение вероятности. Правило для нахождения геометрических вероятностей. Геометрическая модель. | Знать классическую вероятностную схему для равновозможных испытаниях; правило геометрических вероятностей. Уметь по условию текстовой задачи на нахождение вероятности строить геометрическую модель и переходить к корректно поставленной математической задаче. | УС |
|
|
| 118 | Вероятность и геометрия | 1 | КУ | Классическая вероятностная схема. Классическое определение вероятности. Правило для нахождения геометрических вероятностей. Геометрическая модель. | Знать классическую вероятностную схему для равновозможных испытаниях; правило геометрических вероятностей. Уметь по условию текстовой задачи на нахождение вероятности строить геометрическую модель и переходить к корректно поставленной математической задаче. | УС, ФО |
|
|
| 119 | Независимые повторения испытаний с двумя исходами | 1 | УИНМ | Схема Бернулли. Теорема Бернулли. Биномиальное распределение. Многоугольник распределения. | Знать вероятностную схему Бернулли, теорему Бернулли, понятие многогранник распределения. Уметь решать вероятностные задачи, используя вероятностную схему Бернулли, теорему Бернулли, понятие многогранник распределения. | УС |
|
|
| 122 | Независимые повторения испытаний с двумя исходами
| 1 | КУ | Схема Бернулли. Теорема Бернулли. Биномиальное распределение. Многоугольник распределения. | Знать вероятностную схему Бернулли, теорему Бернулли, понятие многогранник распределения. Уметь решать вероятностные задачи, используя вероятностную схему Бернулли, теорему Бернулли, понятие многогранник распределения. | УС, СР |
|
|
| 121 | Независимые повторения испытаний с двумя исходами
| 1 | УЗИ | УС, ФО |
|
|
| 122 | Статистические методы обработки информации
| 1 | УИНМ | Обработка информации. Упорядочивание и группирование данных. Таблицы и графики распределения данных. Паспорт данных. Числовые характеристики. | Знать понятия: общий ряд данных, выборка, варианта, кратность варианты, таблица распределения, частота варианты, график распределения частот; способы представления информации. Уметь определять понятия, приводить доказательства; находить частоту события, используя собственные наблюдения и готовые статистические данные, понимать статистические утверждения, встречающиеся в повседневной жизни. использовать компьютерные технологии для создания базы данных. | УС |
|
|
| 123 | Статистические методы обработки информации | 1 | КУ | УС, СР |
|
|
| 124 | Гауссова кривая. Закон больших чисел
| 1 | УИНМ | Статистическая устойчивость. Гауссова кривая. Кривая нормального распределения. Частота «успеха». Закон больших чисел. | Знать график, какой функции называется гауссовой кривой; алгоритм использования кривой нормального распределения и функции площади под гауссовой кривой в приближенных вычислениях, закон больших чисел. Уметь решать вероятностные задачи, используя знания о гауссовой кривой; алгоритм использования кривой нормального распределения и функции площади под гауссовой кривой в приближенных вычислениях, закон больших чисел. . | УС |
|
|
| 125 | Гауссова кривая. Закон больших чисел | 1 | КУ | УС, ФО |
|
|
|
БЛОК 6. Объёмы тел (19 ч)
|
| 126 | Понятие объёма.
| 1 | КУ | Единицы измерения объема; свойства объемов. | Знать: понятие объема, единицы измерения объемов, свойства объемов. Уметь: воспроизводить правила и примеры. | ФО |
|
|
| 127 | Объём прямоугольного параллелепипеда. | 1 | КУ | Теорема об объеме прямоугольного параллелепипеда; следствия из этой теоремы. | Знать: формулы для вычисления объема прямоугольного параллелепипеда. Уметь: применять изученные формулы к решению различных задач на доказательство и вычисление. | ФО |
|
|
| 128 | Объём прямоугольного параллелепипеда. | 1 | КУ | Теорема об объеме прямоугольного параллелепипеда; следствия из этой теоремы. | Знать: формулы для вычисления объема прямоугольного параллелепипеда. Уметь: применять изученные формулы к решению различных задач на доказательство и вычисление. | СР |
|
|
| 129 | Объём прямой призмы. | 1 | УИНМ | Прямая призма; объём прямой призмы. | Знать: формулы для вычисления объема прямой призмы Уметь: применять формулы при решении простейших задач.
| ФО |
|
|
| 130 | Объём прямой призмы. | 1 | КУ | Прямая призма; объём прямой призмы. | Знать: формулы для вычисления объема прямой призмы Уметь: применять формулы при решении простейших задач. | ФО |
|
|
| 131 | Объём цилиндра. | 1 | УИНМ | Призма вписанная в цилиндр; призма описанная около цилиндра; объем цилиндра. | Знать: формулы для вычисления объема цилиндра Уметь: доказывать теорему об объеме цилиндра. | ФО |
|
|
| 132 | Объём наклонной призмы.
| 1 | УИНМ | Определенный интеграл; объем наклонной призмы. | Знать: определение наклонной призмы; формулу для нахождения объема наклонной призмы. Уметь: применять формулы для решения задач. | ФО |
|
|
| 133 | Объём наклонной призмы. | 1 | УПЗУ | Определенный интеграл; объем наклонной призмы. | Знать: определение наклонной призмы; формулу для нахождения объема наклонной призмы. Уметь: применять формулы для решения задач. | ФО |
|
|
| 134 | Объём пирамиды. | 1 | УИНМ | Пирамида; объем пирамиды. | Знать: формулы для нахождения объема пирамиды. Уметь: доказывать теорему об объеме пирамиды | ФО |
|
|
| 135 | Объём усечённой пирамиды | 1 | КУ | Усеченная пирамида; объем усеченной пирамиды. | Знать: формулу для нахождения объема усеченной пирамиды Уметь: доказывать следствие из теоремы о нахождении объема пирамиды | ФО |
|
|
| 136 | Объём конуса. | 1 | УИНМ | Конус; объем конуса. | Знать: формулу для нахождения объема конуса. Уметь: доказывать теорему об объеме конуса. |
|
|
|
| 137 | Решение задач. | 1 | УПЗУ | Единицы измерения объема; свойства объемов; объем прямоугольного параллелепипеда; объём прямой призмы; объем пирамиды; объем конуса. | Знать: формулы для нахождения объемов прямоугольного параллелепипеда, призмы, пирамиды, конуса, цилиндра. Уметь: находить объемы тел при решении задач. | ФО |
|
|
| 138 | Контрольная работа № 10 по теме: «Объёмы тел» | 1 | КОЗ | Единицы измерения объема; свойства объемов; объем прямоугольного параллелепипеда; объём прямой призмы; объем пирамиды; объем конуса. | Знать: формулы для нахождения объемов прямоугольного параллелепипеда, призмы, пирамиды, конуса, цилиндра. Уметь: решать задачи на нахож. объемов тел. | КР |
|
|
| 139 | Объём шара. | 1 | КУ | Шар; объем шара. | Знать: формулы вычисления объема шара Уметь: применять формулы для решения задач. | ФО |
|
|
| 140 | Объём шарового сегмента, шарового слоя и шарового сектора. | 1 | УИНМ | Шаровой сегмент, шаровой слой, шаровой сектор и их объемы. | Знать: формулы вычисления объема шарового сегмента, слоя и сектора. Уметь: применять формулы для решения задач. | МД |
|
|
| 141 | Площадь сферы. | 1 | УИНМ | Сфера; площадь сферы | Знать: формулу площади сферы Уметь: применять формулы для решения задач. | ФО |
|
|
| 142 | Решение задач.
| 1 | УПЗУ | Объем шара, объем шарового сегмента, шарового слоя и шарового сектора.
| Уметь: решать задачи на нахождение объемов в комбинации тел; развернуто обосновывать суждения. | ФО |
|
|
| 143 | Решение задач | 1 | УПЗУ | Объем шара, объем шарового сегмента, шарового слоя и шарового сектора. | Уметь: решать задачи на нахождение объемов в комбинации тел; развернуто обосновывать суждения |
|
|
|
| 144 | Контрольная работа № 11 по теме: «Объём шара и площадь сферы» | 1 | КОЗ | Объем шара, объем шарового сегмента, шарового слоя и шарового сектора.
| Знать: формулы вычисления объема шара, шарового сегмента, слоя и сектора; площадь сферы. Уметь: свободно пользоваться понятием «объем пространственной фигуры» при решении задач на объем шара, шарового сегмента, шарового слоя и шарового сектора; вычислять объемы тел с помощью определенного интеграла. |
|
|
|
|
БЛОК 7. Уравнения и неравенства. Системы уравнений и неравенств. (33 ч)
|
| 145 | Равносильность уравнений. | 1 | УИНМ | Равносильные уравнения. Область определения уравнения. Утверждение о равносильности уравнений. Этапы решения уравнений: технический, анализ решения, проверка. Теоремы о равносильности уравнений. | Знать определение равносильных уравнений; утверждения и теоремы о равносильности уравнений. Уметь применять изученные теоремы, утверждения на практике. | УС |
|
|
| 146 | Равносильность уравнений. | 1 | КУ | Равносильные уравнения. Область определения уравнения. Утверждение о равносильности уравнений. Этапы решения уравнений: технический, анализ решения, проверка. Теоремы о равносильности уравнений. | Знать определение равносильных уравнений; утверждения и теоремы о равносильности уравнений. Уметь применять изученные теоремы, утверждения на практике. | УС, ФО |
|
|
| 147 | Равносильность уравнений. | 1 | УЗИ | Равносильные уравнения. Область определения уравнения. Утверждение о равносильности уравнений. Этапы решения уравнений: технический, анализ решения, проверка. Теоремы о равносильности уравнений. | Знать определение равносильных уравнений; утверждения и теоремы о равносильности уравнений. Уметь применять изученные теоремы, утверждения на практике. | УС, ФО |
|
|
| 148 | Равносильность уравнений. | 1 | УПЗУ | Равносильные уравнения. Область определения уравнения. Утверждение о равносильности уравнений. Этапы решения уравнений: технический, анализ решения, проверка. Теоремы о равносильности уравнений. | Знать определение равносильных уравнений; утверждения и теоремы о равносильности уравнений. Уметь применять изученные теоремы, утверждения на практике. | УС, СР |
|
|
| 149 | Общие методы решения уравнений
| 1 | УИНМ | Общие методы решения уравнений: замена уравнения h(f(x)) = h(g(x)) уравнением f(x) = g(x), разложение на множители, введение новой переменной, функционально-графический. | Знать основные методы решения алгебраических уравнений: замена уравнения h(f(x)) = h(g(x)) уравнением f(x) = g(x), разложение на множители, метод введения новой переменной, функционально-графический. Уметь применять изученные методы решения уравнений на практике. | УС |
|
|
| 150 | Общие методы решения уравнений
| 1 | КУ | УС, ФО |
|
|
| 151 | Общие методы решения уравнений | 1 | УЗИ | УС, СР |
|
|
| 152 | Равносильность неравенств | 1 | УИНМ | Решение неравенств с одной переменной. Равносильные неравенства. Следствия неравенства. Теоремы о равносильности неравенств с одной переменной. Метод интервалов. | Знать основные способы равносильных переходов. Уметь производить равносильные переходы с целью упрощения уравнения; доказывать равносильность неравенств на основе теорем равносильности; предвидеть возможную потерю или приобретение корня и находить пути возможного избегания ошибок. | УС |
|
|
| 153 | Равносильность неравенств | 1 | КУ | Решение неравенств с одной переменной. Равносильные неравенства. Следствия неравенства. Теоремы о равносильности неравенств с одной переменной. Метод интервалов. | Знать основные способы равносильных переходов. Уметь производить равносильные переходы с целью упрощения уравнения; доказывать равносильность неравенств на основе теорем равносильности; предвидеть возможную потерю или приобретение корня и находить пути возможного избегания ошибок. | УС, ФО |
|
|
| 154 | Равносильность неравенств | 1 | УЗИ | Решение неравенств с одной переменной. Равносильные неравенства. Следствия неравенства. Теоремы о равносильности неравенств с одной переменной. Метод интервалов. | Знать основные способы равносильных переходов. Уметь производить равносильные переходы с целью упрощения уравнения; доказывать равносильность неравенств на основе теорем равносильности; предвидеть возможную потерю или приобретение корня и находить пути возможного избегания ошибок. | УС, СР |
|
|
| 155 | Уравнения и неравенства с модулями. | 1 | УИНМ | Геометрический и графические методы решения уравнений и неравенств с модулями. Раскрытие модуля по определению. | Знать, как решать уравнения и неравенства с модулем, раскрывая модуль по определению, графически и используя свойства функций входящих в выражение. Уметь использовать различные приемы решения уравнений и неравенств с модулем | УС |
|
|
| 156 | Уравнения и неравенства с модулями. | 1 | КУ | Геометрический и графические методы решения уравнений и неравенств с модулями. Раскрытие модуля по определению. | Знать, как решать уравнения и неравенства с модулем, раскрывая модуль по определению, графически и используя свойства функций входящих в выражение. Уметь использовать различные приемы решения уравнений и неравенств с модулем | УС, СР |
|
|
| 157 | Уравнения и неравенства с модулями. | 1 | УПКЗУ | Геометрический и графические методы решения уравнений и неравенств с модулями. Раскрытие модуля по определению. | Знать, как решать уравнения и неравенства с модулем, раскрывая модуль по определению, графически и используя свойства функций входящих в выражение. Уметь использовать различные приемы решения уравнений и неравенств с модулем | УС, ФО |
|
|
| 158 | Контрольная работа № 12 по теме «Общие методы решения уравнений. Равносильность уравнений и неравенств» | 1 | КОЗ | Равносильные уравнения и неравенства. Теоремы о равносильности уравнений и неравенств. Метод интервалов. Геометрический и графические методы решения уравнений и неравенств с модулями. Раскрытие модуля по определению. | Знать теоретический материал, изученный на предыдущих уроках. Уметь применять полученные знания, умения и навыки на практике. | КР |
|
|
| 159 | Контрольная работа № 12 по теме «Общие методы решения уравнений. Равносильность уравнений и неравенств» | 1 | КОЗ | Равносильные уравнения и неравенства. Теоремы о равносильности уравнений и неравенств. Метод интервалов. Геометрический и графические методы решения уравнений и неравенств с модулями. Раскрытие модуля по определению. | Знать теоретический материал, изученный на предыдущих уроках. Уметь применять полученные знания, умения и навыки на практике. | КР |
|
|
| 160 | Уравнения и неравенства со знаком радикала
| 1 | УИНМ | Иррациональные уравнения и неравенства. Метод возведения обеих частей уравнения в одну и туже степень. Способы проверки корней уравнения. Метод введения новой переменной. Совокупность систем неравенств. | Знать основной метод решения иррациональных уравнений и неравенств – метод возведения обеих частей уравнения в одну и туже степень, а также некоторые специфические приемы (введение новой переменной). Уметь использовать метод возведения обеих частей уравнения в одну и туже степень, а также некоторые специфические приемы (введение новой переменной). | УС |
|
|
| 161 | Уравнения и неравенства со знаком радикала | 1 | КУ | УС, ФО |
|
|
| 162 | Уравнения и неравенства со знаком радикала | 1 | УЗИ | УС, СР |
|
|
| 163 | Доказательство неравенств | 1 | УИНМ | Неравенство Коши. Синтетический метод доказательств неравенств. Доказательство неравенств методом от противного. Доказательство неравенств методом математической индукции. Функционально-графические методы доказательств неравенств. | Знать, что доказать неравенства можно с помощью определения, от противного, методом математической индукции, функционально – графическим методом, а также синтетическим методом. Уметь использовать для доказательства неравенства методы: с помощью определения, от противного, метода математической индукции, функционально – графического метода, а также синтетический метод. | УС |
|
|
| 164 | Доказательство неравенств | 1 | КУ | Неравенство Коши. Синтетический метод доказательств неравенств. Доказательство неравенств методом от противного. Доказательство неравенств методом математической индукции. Функционально-графические методы доказательств неравенств. | Знать, что доказать неравенства можно с помощью определения, от противного, методом математической индукции, функционально – графическим методом, а также синтетическим методом. Уметь использовать для доказательства неравенства методы: с помощью определения, от противного, метода математической индукции, функционально – графического метода, а также синтетический метод. | УС, ФО |
|
|
| 165 | Доказательство неравенств | 1 | УЗИ | Неравенство Коши. Синтетический метод доказательств неравенств. Доказательство неравенств методом от противного. Доказательство неравенств методом математической индукции. Функционально-графические методы доказательств неравенств. | Знать, что доказать неравенства можно с помощью определения, от противного, методом математической индукции, функционально – графическим методом, а также синтетическим методом. Уметь использовать для доказательства неравенства методы: с помощью определения, от противного, метода математической индукции, функционально – графического метода, а также синтетический метод. | УС, СР |
|
|
| 166 | Уравнения и неравенства с двумя переменными. | 1 | УИНМ | Диофантово уравнение. Целочисленные решения уравнения с двумя переменными. Графический способ решения неравенств с двумя переменными. Системы неравенств с двумя переменными. | Знать и понимать решения уравнений и неравенств с двумя переменными Уметь изображать на плоскости множество решений уравнений и неравенств с двумя переменными; обосновывать суждения, давать определения, приводить доказательства, примеры. | УС |
|
|
| 167 | Уравнения и неравенства с двумя переменными. | 1 | КУ | Диофантово уравнение. Целочисленные решения уравнения с двумя переменными. Графический способ решения неравенств с двумя переменными. Системы неравенств с двумя переменными. | Знать и понимать решения уравнений и неравенств с двумя переменными Уметь изображать на плоскости множество решений уравнений и неравенств с двумя переменными; обосновывать суждения, давать определения, приводить доказательства, примеры . | УС, СР |
|
|
| 168 | Системы уравнений | 1 | УИНМ | Иррациональные системы уравнений. Тригонометрические системы уравнений.. Равносильные системы уравнений. Этапы решения задачи с помощью систем уравнений: составление математической модели; работа с составленной моделью; ответ на вопрос задачи.
| Знать, как решать графически и аналитически системы, составленные из двух и более уравнений. Уметь свободно применять различные способы при решении систем уравнений; самостоятельно искать, и отбирать необходимую для решения учебных задач информацию. | УС |
|
|
| 169 | Системы уравнений | 1 | КУ | Иррациональные системы уравнений. Тригонометрические системы уравнений.. Равносильные системы уравнений. Этапы решения задачи с помощью систем уравнений: составление математической модели; работа с составленной моделью; ответ на вопрос задачи. | Знать, как решать графически и аналитически системы, составленные из двух и более уравнений. Уметь свободно применять различные способы при решении систем уравнений; самостоятельно искать, и отбирать необходимую для решения учебных задач информацию. | УС, ФО |
|
|
| 170 | Системы уравнений | 1 | УЗИ | Иррациональные системы уравнений. Тригонометрические системы уравнений.. Равносильные системы уравнений. Этапы решения задачи с помощью систем уравнений: составление математической модели; работа с составленной моделью; ответ на вопрос задачи. | Знать, как решать графически и аналитически системы, составленные из двух и более уравнений. Уметь свободно применять различные способы при решении систем уравнений; самостоятельно искать, и отбирать необходимую для решения учебных задач информацию. | УС, СР |
|
|
| 171 | Системы уравнений | 1 | УПКЗУ | Иррациональные системы уравнений. Тригонометрические системы уравнений.. Равносильные системы уравнений. Этапы решения задачи с помощью систем уравнений: составление математической модели; работа с составленной моделью; ответ на вопрос задачи. | Знать, как решать графически и аналитически системы, составленные из двух и более уравнений. Уметь свободно применять различные способы при решении систем уравнений; самостоятельно искать, и отбирать необходимую для решения учебных задач информацию. | УС, ФО |
|
|
| 172 | Контрольная работа № 14 по теме «Уравнения и неравенства со знаком радикала. Системы уравнений» | 1 | КОЗ | Иррациональные уравнения и неравенства. Неравенство Коши. Синтетический метод доказательств неравенств. Доказательство неравенств методом от противного. Доказательство неравенств методом математической индукции. Диофантово уравнение. Целочисленные решения уравнения с двумя переменными. Равносильные системы уравнений. Этапы решения задачи с помощью систем уравнений. | Знать теоретический материал, изученный на предыдущих уроках. Уметь применять полученные знания, умения и навыки на практике. | КР |
|
|
| 173 | Контрольная работа № 14 по теме «Уравнения и неравенства со знаком радикала. Системы уравнений» | 1 | КОЗ | Иррациональные уравнения и неравенства. Неравенство Коши. Синтетический метод доказательств неравенств. Доказательство неравенств методом от противного. Доказательство неравенств методом математической индукции. Диофантово уравнение. Целочисленные решения уравнения с двумя переменными. Равносильные системы уравнений. Этапы решения задачи с помощью систем уравнений. | Знать теоретический материал, изученный на предыдущих уроках. Уметь применять полученные знания, умения и навыки на практике. | КР |
|
|
| 174 | Задачи с параметрами | 1 | УИНМ | Уравнение с параметром. Неравенства с параметром. | Знать определение уравнения с параметром Уметь решать уравнения и неравенства с параметром. | УС
|
|
|
| 175 | Задачи с параметрами
| 1 | КУ | УС, ФО |
|
|
| 176 | Задачи с параметрами
| 1 | УЗИ | УС, СР |
|
|
| 177 | Задачи с параметрами
| 1 | УПЗУ | УС, ФО |
|
|
|
БЛОК 8. Обобщающее повторение (26 ч)
|
| 178 | Повторение. Треугольники. | 1 | КУ | Признаки равенства треугольников. Медианы, биссектрисы и медианы треугольника. | Знать: основные определения и теоремы по теме «Треугольники». Уметь: решать задачи по теме |
|
|
|
| 179 | Повторение. Четырёхугольники. | 1 | УПЗУ | Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции; равнобедренная и прямоугольная трапеции. | Знать: основные определения и теоремы по теме «Четырёхугольники». Уметь: решать задачи по теме | СР |
|
|
| 180 | Повторение. Преобразование выражений, содержащих радикалы и степени с дробными показателями. | 1 | УОСЗ | Иррациональные выражения; вынесение множителя за знак радикала; внесение множителя под знак радикала | Знать, как выполнять арифметические действия, сочетая устные и письменные приемы; как находить значения корня натуральной степени по известным формулам и правилам преобразования буквенных выражений, включающих радикалы. Уметь выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени по известным формулам и правилам преобразования буквенных выражений, включающих радикалы | УС, ФО |
|
|
| 181 | Повторение. Преобразования тригонометрических выражений. | 1 | УОСЗ | Тригонометрические выражения | Уметь преобразовывать тригонометрические выражения | УС, СР |
|
|
| 182 | Повторение. Преобразования выражений, содержащих степени и логарифмы. | 1 | УОСЗ | Выражения, содержащие степени и логарифмы. | Уметь преобразовывать выражения, содержащие степени и логарифмы. | УС, ФО |
|
|
| 183 | Повторение. Рациональные функции. | 1 | УОСЗ | Рациональные функции, их свойства и графики | Уметь определять значение функции по значению аргумента при различных способах задания функции; применять свойства рациональных функций | УС, ФО |
|
|
| 184 | Повторение. Окружность.
| 1 | УПЗУ | Описанная окружность. Вписанная окружность. | Знать основные определения и теоремы по теме «Окружность». Уметь решать задачи по данной теме. | ФО |
|
|
| 185 | Повторение. Метод координат. Векторы. | 1 | УПЗУ | Координаты вектора. Простейшие задачи в координатах. Уравнение окружности и прямой. | Знать основные определения и теоремы по теме «Метод координат. Векторы». Уметь решать задачи по данной теме. | ФО |
|
|
| 186 | Повторение. Аксиомы стереометрии и их следствия.
| 1 | УПЗУ | Аксиомы стереометрии и их следствия.
| Знать: аксиомы стереометрии и следствия из них. Уметь: решать задачи по данной теме. | ФО |
|
|
| 187 | Повторение. Тригонометрические функции. | 1 | УОСЗ | Тригонометрические функции числового аргумента | Знать знаки тригонометрических функций в зависимости от расположения точки, изображающей число на числовой окружности. Уметь строить графики тригонометрических функций, решать простейшие тригонометрические уравнения и неравенства | УС, ФО |
|
|
| 188 | Повторение. Степенная, показательная и логарифмическая функции. | 1 | УОСЗ | Показательная функция. Свойства и график показательной функции. Экспонента. Логарифм. Логарифмическая функция, свойства функции и ее график. | Знать определение логарифмической и показательной функций, их свойства в зависимости от основания. Уметь определять значение функции по значению аргумента при различных способах задания функции; применять свойства логарифмической и показательной функций. | УС, СР |
|
|
| 189 | Повторение. Рациональные уравнения и неравенства. | 1 | УОСЗ | Рациональные уравнения и неравенства. | Уметь решать рациональные уравнения и неравенства | УС, ФО |
|
|
| 190 | Повторение. Иррациональные уравнения и неравенства. | 1 | УОСЗ | Иррациональные уравнения и неравенства. Метод возведения обеих частей уравнения в одну и туже степень. Способы проверки корней уравнения. Метод введения новой переменной. Совокупность систем неравенств. | Знать основной метод решения иррациональных уравнений и неравенств – метод возведения обеих частей уравнения в одну и туже степень, а также некоторые специфические приемы (введение новой переменной). Уметь использовать метод возведения обеих частей уравнения в одну и туже степень, а также некоторые специфические приемы (введение новой переменной). | УС, ФО |
|
|
| 191 | Повторение. Взаимное расположение прямой и плоскости.
| 1 | УПЗУ | Параллельность прямой и плоскости; перпендикулярность прямой и плоскости. | Знать: взаимное расположение прямой и плоскости Уметь: решать задачи по данной теме | ФО |
|
|
| 192 | Повторение. Взаимное расположение плоскостей.
| 1 | УПЗУ | Параллельные плоскости; свойства параллельных плоскостей; перпендикулярность плоскостей. | Знать: взаимное расположение плоскостей. Уметь: решать задачи по данной теме | ФО |
|
|
| 193 | Повторение. Перпендикулярность прямых, прямой и плоскости, плоскостей.
| 1 | УПЗУ | Перпендикулярные прямые в пространстве, признак перпендикулярности прямой и плоскости, теорема о трёх перпендикулярах, двугранный угол, линейный угол двугранного угла, расстояние от точки до плоскости, прямоугольный параллелепипед. | Уметь: находить наклонную или ее проекцию, используя соотношения в прямоугольном треугольнике; находить угол между диагональю прямоугольного параллелепипеда и одной из его граней; доказывать перпендикулярность прямой и плоскости, используя признак перпендикулярности, теорему о трех перпендикулярах | ФО |
|
|
| 194 | Повторение. Тригонометрические уравнения и неравенства. | 1 | УОСЗ | Тригонометрические уравнения и неравенства. Методы решения тригонометрических уравнений. | Уметь: решать тригонометрические уравнения различными способами. | УС, СР |
|
|
| 195 | Повторение. Показательные уравнения и неравенства. | 1 | УПКЗУ | Степень с иррациональным показателем. Показательная функция. Свойства и график показательной функции. Экспонента. Показательные уравнения и неравенства | Знать определение показательного уравнения и неравенства. Уметь решать показательные уравнения и неравенства | УС, ФО |
|
|
| 196 | Итоговая контрольная работа по математике | 1 | КОЗ | Проверка знаний, умений и навыков за курс математики 11 класса | Уметь решать задачи по темам, изученным в курсе математики 11 класса | КР |
|
|
| 197 | Итоговая контрольная работа по математике | 1 | КОЗ | Проверка знаний, умений и навыков за курс математики 11 класса | Уметь решать задачи по темам, изученным в курсе математики 11 класса | КР |
|
|
| 198 | Повторение. Решение задач.
| 1 | УОСЗ |
| Уметь: решать задачи различных видов | СР |
|
|
| 199 | Повторение. Цилиндр, конус, шар.
| 1 | УПЗУ | Конус, цилиндр, шар, сфера, площадь поверхности конуса, цилиндра; площадь сферы; уравнение сферы; касательная плоскость к сфере; точка касания; свойство касательной плоскости; три случая взаимного расположения сферы и плоскости. | Знать: понятия: цилиндр, конус, шар. Уметь: изображать многогранники, выполнять чертежи по условиям задач и решать простейшие задачи. | ФО |
|
|
| 200 | Повторение. Системы иррациональных уравнений. | 1 | УОСЗ | Системы иррациональных уравнений. | Уметь решать системы иррациональных уравнений. | УС, ФО |
|
|
| 201 | Повторение. Системы тригонометрических уравнений. | 1 | УОСЗ | Системы тригонометрических уравнений. | Уметь решать системы тригонометрических уравнений. | УС, СР |
|
|
| 202 | Повторение. Объёмы тел. | 1 | УПЗУ | Единицы измерения объема; свойства объемов; объем прямоугольного параллелепипеда; объём прямой призмы; объем пирамиды; объем конуса. | Знать: формулы для нахождения объемов прямоугольного параллелепипеда, призмы, пирамиды, конуса, цилиндра. Уметь: решать задачи на нахождение объемов тел. | СР |
|
|
| 203 | Повторение. Логарифмические уравнения и неравенства. | 1 | УОСЗ | Логарифмические уравнения и неравенства.
| Уметь решать логарифмические уравнения и неравенства | УС, ФО |
|
|
| 204 | Итоговый урок | 1 | УОСЗ |
|
| УС, ФО |
|
|
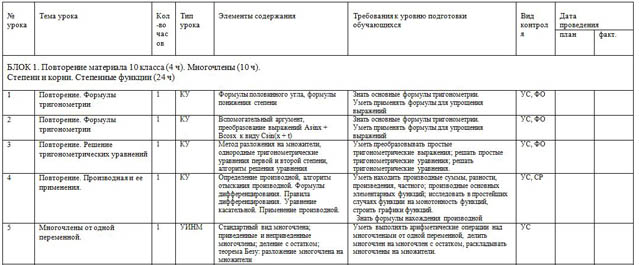

 Получите свидетельство
Получите свидетельство Вход
Вход


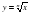 , их свойства и графики. Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы. Понятие степени с любым рациональным показателем. Степенные функции, их свойства и графики.
, их свойства и графики. Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы. Понятие степени с любым рациональным показателем. Степенные функции, их свойства и графики. -1), тригонометрических функций. Простейшие правила нахождения первообразных.
-1), тригонометрических функций. Простейшие правила нахождения первообразных. 








 Рабочая программа по математике (11 класс) (0.11 MB)
Рабочая программа по математике (11 класс) (0.11 MB)
 0
0 570
570 89
89 Нравится
0
Нравится
0


