Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №33 с углубленным изучение отдельных предметов»
| РАССМОТРЕНО
на заседании МО учителей математики
Протокол от«__» ________2011 г. № _____
| СОГЛАСОВАНО
заместитель директора МОУ «СОШ №33» ________Ансимова Т.Г. (подпись)
| РАССМОТРЕНО
на заседании педагогического совета
Протокол от «__» ______2011 г. № _____
| УТВЕРЖДАЮ
Директор МОУ «СОШ №33»
___________Бредихин А.Н. (подпись)
|
РАБОЧАЯ ПРОГРАММА
Провоторовой Елены Викторовны
учителя математики
по учебному курсу
« Алгебра и начала математического анализа»
10в, 10г класса (профильный уровень)
Старый Оскол
2011
Пояснительная записка
Данная рабочая программа ориентирована на учащихся 10в и 10г классов и реализуется на основе следующих документов:
1. Программы общеобразовательных учреждений. Алгебра и начала математического анализа. 10-11 классы,- М. Просвещение, 2009, составитель Т.А. Бурмистрова.
2. Стандарта среднего (полного) общего образования по математике (профильный уровень).
3. Инструктивно-методического письма «О преподавании математики в 2011-2012 учебном году в общеобразовательных учреждениях Белгородской области»
Программа соответствует учебнику «Алгебра и начала математического анализа» для 10 класса образовательных учреждений, - М. Просвещение, 2009, С. М. Никольский, М.К. Потапов, Н.Н. Решетников и др., дидактический материал «Алгебра и начала математического анализа» для 10 класса, - М. Просвещение, 2009, М.К. Потапов, А.В. Шевкин.
Основной задачей курса является подготовка обучающихся на уровне требований, предъявляемых Обязательным минимумом содержания образования по математике.
Изучение математики на профильном уровне среднего (полного) общего образования направлено на достижение следующих целей:
-формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
-овладение языком математики в устной и письменной форме, математическими знаниями и умениями, необходимыми для изучения школьных естественнонаучных дисциплин, продолжения образования и освоения избранной специальности на современном уровне;
-развитие логического мышления, алгоритмической культуры, пространственного воображения, математического мышления и интуиции, творческих способностей, необходимых для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
-воспитание средствами математики культуры личности через знакомство с историей развития математики, эволюцией математических идей;
- понимания значимости математики для научно-технического прогресса.
Согласно федеральному базисному учебному плану на изучение математики в профильном уровне в 10 классе отводится не менее 204 часов из расчета 6 ч в неделю, при этом разделение часов на изучение алгебры и геометрии следующее:
4 часа в неделю алгебры и 2 часа в неделю геометрии в течение всего учебного года, итого 136 часов алгебры и 68 часов геометрии. В связи с продлением учебного года с 34 недель до 35 недель общее количество часов по алгебре составило 140 часов. 4 часа добавила в итоговое повторение в конце года. Считаю, что такое распределение часов наиболее эффективно.
Текущий контроль знаний, умений и навыков проводится в виде 8 контрольных и 15 самостоятельных работ, 5 тестов, 3 зачётов.
Курс строится на индуктивной основе с привлечением элементов дедуктивных рассуждений. Теоретический материал курса излагается на наглядно-интуитивном уровне, математические методы и законы формулируются в виде правил.
Система уроков условна, но всё же выделяются следующие виды: урок-лекция, урок-практикум, урок-исследование, комбинированный урок, урок решения задач, урок-тест, урок - самостоятельная работа, урок - контрольная работа. Формы организации учебного процесса: индивидуальные, групповые, индивидуально-групповые, фронтальные, практикумы.
Требования к уровню подготовки учащихся
В результате изучения математики на профильном уровне в старшей школе ученик должен
Знать/понимать1
значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
вероятностных характер различных процессов и закономерностей окружающего мира.
Числовые и буквенные выражения
Уметь:
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
применять понятия, связанные с делимостью целых чисел, при решении математических задач;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, при необходимости используя справочные материалы и простейшие вычислительные устройства.
Функции и графики
Уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
Начала математического анализа
Уметь
находить сумму бесконечно убывающей геометрический прогрессии;
Уравнения и неравенства
Уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
доказывать несложные неравенства;
решать текстовые задачи с помощью составления уравнений, и неравенств, интерпретируя результат с учетом ограничений условия задачи;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем;
находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
Элементы комбинаторики, статистики и теории вероятностей
Уметь:
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
вычислять, в простейших случаях, вероятности событий на основе подсчета числа исходов.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для
КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ (УЧЕБНО – ТЕМАТИЧЕСКИЙ ПЛАН)
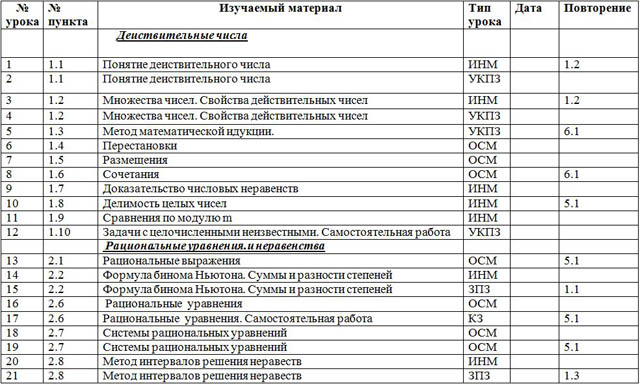
| № урока | № пункта | Изучаемый материал | Тип урока | Дата | Повторение |
|
|
| Деиствительные числа |
|
|
|
| 1 | 1.1 | Понятие деиствительного числа | ИНМ |
| 1.2 |
| 2 | 1.1 | Понятие деиствительного числа | УКПЗ |
|
|
| 3 | 1.2 | Множества чисел. Свойства действительных чисел | ИНМ |
| 1.2 |
| 4 | 1.2 | Множества чисел. Свойства действительных чисел | УКПЗ |
|
|
| 5 | 1.3 | Метод математической идукции. | УКПЗ |
| 6.1 |
| 6 | 1.4 | Перестановки | ОСМ |
|
|
| 7 | 1.5 | Размещения | ОСМ |
|
|
| 8 | 1.6 | Сочетания | ОСМ |
| 6.1 |
| 9 | 1.7 | Доказательство числовых неравенств | ИНМ |
|
|
| 10 | 1.8 | Делимость целых чисел | ИНМ |
| 5.1 |
| 11 | 1.9 | Сравнения по модулю m | ИНМ |
|
|
| 12 | 1.10 | Задачи с целочисленными неизвестными. Самостоятельная работа | УКПЗ |
|
|
|
|
| Рациональные уравнения.и неравенства |
|
|
|
| 13 | 2.1 | Рациональные выражения | ОСМ |
| 5.1 |
| 14 | 2.2 | Формула бинома Ньютона. Суммы и разности степеней | ИНМ |
|
|
| 15 | 2.2 | Формула бинома Ньютона. Суммы и разности степеней | ЗПЗ |
| 1.1 |
| 16 | 2.6 | Рациональные уравнения | ОСМ |
|
|
| 17 | 2.6 | Рациональные уравнения. Самостоятельная работа | КЗ |
| 5.1 |
| 18 | 2.7 | Системы рациональных уравнений | ОСМ |
|
|
| 19 | 2.7 | Системы рациональных уравнений | ОСМ |
| 5.1 |
| 20 | 2.8 | Метод интервалов решения неравеств | ИНМ |
|
|
| 21 | 2.8 | Метод интервалов решения неравеств | ЗПЗ |
| 1.3 |
| 22 | 2.8 | Метод интервалов решения неравеств. Тест | ПР |
|
|
| 23 | 2.9 | Рациональные неравенства | ИНМ |
|
|
| 24 | 2.9 | Рациональные неравенства | ЗПЗ |
| 1.3 |
| 25 | 2.9 | Рациональные неравенства. Самостоятельная работа | ПР |
|
|
| 26 | 2.10 | Нестрогие неравенства | ИНМ |
| 2.1 |
| 27 | 2.10 | Нестрогие неравенства | ЗПЗ |
|
|
| 28 | 2.10 | Нестрогие неравенства | ПР |
| 2.1 |
| 29 | 2.11 | Системы рациональных неравенств. Зачет | КЗ |
|
|
| 30 |
| Контрольная работа N 1 «Рациональные уравнения и неравенства» | КЗ |
|
|
|
|
| Корень степени n |
|
|
|
| 31 | 3.1 | Понятие функции и ее графика | ОСМ |
| 3.1 |
| 32 | 3.2 | Функция у = хn | ИНМ |
|
|
| 33 | 3.2 | Функция у = хn | ЗПЗ |
|
|
| 34 | 3.3 | Понятие корня степени n | ОСМ |
| 6.1 |
| 35 | 3.4 | Корни четной и нечетной степени | ИНМ |
|
|
| 36 | 3.4 | Корни четной и нечетной степени | УЗ |
|
|
| 37 | 3.5 | Арифметический корень | ИНМ |
| 6.2 |
| 38 | 3.5 | Арифметический корень | УКПЗ |
|
|
| 39 | 3.6 | Свойства корня степени n | ИНМ |
|
|
| 40 | 3.6 | Свойства корня степени n | УКПЗ |
| 6.3 |
| 41 | 3.7 | Функция y=nx, x≥0. Тест | ИНМ |
|
|
| 42 |
| Контрольная работа №2 «Корень степени n» | КЗ |
|
|
| |
| Степень положительного числа |
|
|
|
| 43 | 4.1 | Степень с рациональным показателем | ИНМ |
| 1.1 |
| 44 | 4.2 | Свойства степени с рациональным показателем | УКПЗ |
|
|
| 45 | 4.2 | Свойства степени с рациональным показателем. Самостоятельная работа | УЗ |
|
|
| 46 | 4.3 | Понятие предела последовательности | ИНМ |
| 1.2 |
| 47 | 4.3 | Понятие предела последовательности | ЗПЗ |
|
|
| 48 | 4.4 | Свойства пределов | ИНМ |
|
|
| 49 | 4.4 | Свойства пределов | ЗПЗ |
| 1.3 |
| 50 | 4.5 | Бесконечно убывающая геометрическая прогрессия | ИНМ |
|
|
| 51 | 4.6 | Число е | ИНМ |
|
|
| 52 | 4.7 | Понятие степени с иррациональным показателем | ИНМ |
| 2.1 |
| 53 | 4.8 | Показательная функция | ИНМ |
|
|
| 54 | 4.8 | Показательная функция. Зачет | УКПЗ |
|
|
| 55 |
| Контрольная работа №3 «Степень положительного числа» | КЗ |
|
|
|
|
| Логарифмы |
|
|
|
| 56 | 5.1 | Понятие логарифма | ИНМ |
| 2.2 |
| 57 | 5.1 | Понятие логарифма | УЗ |
|
|
| 58 | 5.2 | Свойства логарифмов | ИНМ |
|
|
| 59 | 5.2 | Свойства логарифмов | УЗ |
| 2.3 |
| 60 | 5.2 | Свойства логарифмов. Самостоятельная работа | ОСМ |
|
|
| 61 | 5.3 | Логарифмическая функция | ИНМ |
|
|
|
|
| Показательные и логарифмические уравнения и неравенства |
|
|
|
| 62 | 6.1 | Простейшие показательные уравнения | ИНМ |
| 3.1 |
| 63 | 6.2 | Простейшие логарифмические уравнения | УЗ |
|
|
| 64 | 6.3 | Уравнения , сводящиеся к простейшим заменой переменного | ИНМ |
|
|
| 65 | 6.3 | Уравнения , сводящиеся к простейшим заменой переменного. Самостоятельная работа | УЗ |
|
|
| 66 | 6.4 | Простейшие показательные неравенства | ИНМ |
| 5.1 |
| 67 | 6.4 | Простейшие показательные неравенства | УЗ |
|
|
| 68 | 6.5 | Простейшие логарифмические неравенства | ИНМ |
|
|
| 69 | 6.5 | Простейшие логарифмические неравенства | УЗ |
| 5.3 |
| 70 | 6.6 | Неравенства, сводящиеся к простейшим заменой неизвестного | ИНМ |
|
|
| 71 | 6.6 | Неравенства, сводящиеся к простейшим заменой неизвестного. Самостоятельная работа | УКПЗ |
|
|
| 72 |
| Контрольная работа N4 «Показательные и логарифмические уравнения и неравенства» | КЗ |
|
|
|
|
| Синус и косинус угла |
|
|
|
| 73 | 7.1 | Понятие угла | ИНМ |
| 6.1 |
| 74 | 7.2 | Радианная мера угла | ИНМ |
|
|
| 75 | 7.3 | Определение синуса и косинуса угла | ОСМ |
|
|
| 76 | 7.4 | Основные формулы для синуса и косинуса угла | ИНМ |
| 6.2 |
| 77 | 7.4 | Основные формулы для синуса и косинуса угла. Самостоятельная работа | УКПЗ |
|
|
| 78 | 7.5 | Арксинус | ИНМ |
|
|
| 79 | 7.6 | Арккосинус | ИНМ |
| 6.3 |
|
|
| § 8. Тангенс и котангенс угла |
|
|
|
| 80 | 8.1 | Определение тангенса и котангенса угла | ОСМ |
| 1.1 |
| 81 | 8.2 | Основные формулы для tg a и ctg a | ИНМ |
|
|
| 82 | 8.2 | Основные формулы для tg a и ctg a. Самостоятельная работа | УКПЗ |
|
|
| 83 | 8.3 | Арктангенс | ИНМ |
| 1.2 |
| 84 | 8.4 | Арккотангенс. Тест | ИНМ |
|
|
| 85 |
| Контрольная работа N 5 «Синус, косинус, тангенс, котангенс» | КЗ |
|
|
|
|
| Формулы сложения |
|
|
|
| 86 | 9.1 | Косинус разности и косинус суммы двух углов | ИНМ |
| 1.3 |
| 87 | 9.1 | Косинус разности и косинус суммы двух углов | УКПЗ |
|
|
| 88 | 9.2 | Формулы для дополнительных углов | ИНМ |
|
|
| 89 | 9.3 | Синус суммы и синус разности двух углов | ИНМ |
| 2.1 |
| 90 | 9.3 | Синус суммы и синус разности двух углов. Самостоятельная работа | УЗ |
|
|
| 91 | 9.4 | Сумма и разность синусов косинусов | ИНМ |
| 2.2 |
| 92 | 9.4 | Сумма и разность синусов косинусов | ПР |
|
|
| 93 | 9.5 | Формулы двойных и половинных углов | ИНМ |
| 2.3 |
| 94 | 9.5 | Формулы двойных и половинных углов | ПР |
|
|
| 95 | 9.6 | Произведение синусов и косинусов. Самостоятельная работа | УКПЗ |
|
|
| 96 | 9.7 | Формулы для тангенсов | УКПЗ |
| 3.1 |
|
|
| Тригонометрические функции числового аргумента |
|
|
|
| 97 | 10.1 | Функция y=sinx | ИНМ |
|
|
| 98 | 10.1 | Функция y=sinx | ЗПЗ |
| 5.1 |
| 99 | 10.2 | Функция y=cosx | ИНМ |
|
|
| 100 | 10.2 | Функция y=cosx | УЗ |
|
|
| 101 | 10.3 | Функция y=tgx | ИНМ |
| 5.1 |
| 102 | 10.3 | Функция y=tgx | ПР |
|
|
| 103 | 10.4 | Функция y=ctgx | ИНМ |
|
|
| 104 | 10.4 | Функция y=ctgx. Зачет | УКПЗ |
|
|
| 105 |
| Контрольная работа N 6 «Тригонометрические формулы» | КЗ |
|
|
|
|
| Тригонометрические уравнения и неравенства |
|
|
|
| 106 | 11.1 | Простейшие тригонометрические уравнения. | ИНМ |
| 5.2 |
| 107 | 11.1 | Простейшие тригонометрические уравнения. | ПР |
|
|
| 108 | 11.2 | Уравнения, сводящиеся к простейшим заменой неизвестного. | ИНМ |
|
|
| 109 | 11.2 | Уравнения, сводящиеся к простейшим заменой неизвестного. | УКПЗ |
| 5.2 |
| 110 | 11.3 | Применение основных тригонометрических формул для решения уравнений | УКПЗ |
|
|
| 111 | 11.3 | Применение основных тригонометрических формул для решения уравнений. Самостоятельная работа | ОСМ |
|
|
| 112 | 11.4 | Однородные уравнения | ИНМ |
| 5.3 |
| 113 | 11.5 | Простейшие неравенства для синуса и косинуса. | ИНМ |
|
|
| 114 | 11.6 | Простейшие неравенства для тангенса, котангенса. | ИНМ |
|
|
| 115 | 11.7 | Неравенства, сводящиеся к простейшим заменой неизвестного.Тест | ПР |
|
|
| 116 | 11.8 | Введение вспомогательного угла | ИНМ |
| 6.1 |
| 117 |
| Контрольная работа N 7 «Тригонометрические уравнения и неравенства» | КЗ |
|
|
|
|
| Вероятность события |
|
|
|
| 118 | 12.1 | Понятие вероятности события | ИНМ |
|
|
| 119 | 12.1 | Понятие вероятности события | ЗПЗ |
| 6.2 |
| 120 | 12.1 | Понятие вероятности события | УКПЗ |
|
|
| 121 | 12.2 | Свойства вероятностей | ИНМ |
|
|
| 122 | 12.2 | Свойства вероятностей | УЗ |
| 6.3 |
| 123 | 12.2 | Свойства вероятностей. Самостоятельная работа | УКПЗ |
|
|
|
|
| Частота. Условная вероятность |
|
|
|
| 124 | 13.1 | Относительная частота события | ИНМ |
|
|
| 125 | 13.2 | Условная вероятность. Независимые события | ИНМ |
| 1.1 |
|
|
| Повторение |
|
|
|
| 126 | 2.6, 2.7 | Рациональные уравнения и неравенства | ПМ |
| 2.3 |
| 127 | 2.6, 2.7 | Рациональные уравнения и неравенства | ПР |
| 2.3 |
| 128 | 2.6, 2.7 | Рациональные уравнения и неравенства. Самостоятельная работа | УЗ |
| 2.3 |
| 129 | 3.5, 3.6 | Корень степени n | ОСМ |
| 1.3 |
| 130 | 4.2, 4.7 | Cтепень положительного числа | ОСМ |
| 1.3 |
| 131 | 5.2 | Логарифмы. Тест | ОСМ |
| 1.3 |
| 132 | 6.1-6.6 | Показательные и логарифмические уравнения и неравенства | ПМ |
| 2.3 |
| 133 | 6.1-6.6 | Показательные и логарифмические уравнения и неравенства | ПР |
| 2.3 |
| 134 | 6.1-6.6 | Показательные и логарифмические уравнения и неравенства. Самостоятельная работа | УКПЗ |
| 2.3 |
| 135 | 9.1-9.7 | Формулы тригонометрии | ОСМ |
| 5.1 |
| 136 | 11.1-11.8 | Решение тригонометрических уравнений | ОСМ |
| 5.1 |
| 137 | 11.1-11.8 | Решение тригонометрических уравнений | ПР |
| 5.2 |
| 138 | 11.1-11.8 | Решение тригонометрических уравнений. Самостоятельная работа | УКПЗ |
| 5.2 |
| 139 |
| Итоговая контрольная работа | КЗ |
|
|
| 140 |
| Обобщающее повторение | ОСМ |
|
|
Условные обозначения:
| № п/п | Сокращённое обозначение | Учебное занятие |
| 1 | ИНМ | Изучение нового материала |
| 2 | ЗПЗ | Закрепление первичных знаний |
| 3 | УКПЗ | Урок комплексного применения знаний |
| 4 | КЗ | Контроль знаний |
| 5 | УЗ | Урок закрепления |
| 6 | ОСМ | Урок обобщения и систематизации знаний |
| 8 | ППМ | Повторение пройденного материала |
| 9 | ПР | Практикум |
| 10 | ПМ | Повторение материала по теме |
Содержание программы и учебного курса
Целые и действительные числа (12 часов).
Делимость целых чисел. Деление с остатком. Сравнения. Решение задач с целочисленными неизвестными.
Понятие действительного числа. Свойства действительных чисел. Множества чисел и операции над множествами чисел. Доказательство неравенств. Неравенство о среднем арифметическом и среднем геометрическом двух чисел.
Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач.
Рациональные уравнения и неравенства (18 часов).
Рациональные выражения. Формула бинома Ньютона, свойства биноминальных коэффициентов, треугольник Паскаля, формулы разности и суммы степеней.
Многочлены от одной переменной. Деление многочленов. Деление многочленов с остатком. Рациональные корни многочленов с целыми коэффициентами. Решение целых алгебраических уравнений. Схема Горнера. Теорема Безу. Число корней многочлена.
Рациональные уравнения и неравенства, системы рациональных неравенств.
Корень степени n (12 часов)
Понятие функции, ее области определения и множества значений. Функция y = xn, где n N, ее свойства и график. Понятие корня степени n1 и его свойства, понятие арифметического корня.
N, ее свойства и график. Понятие корня степени n1 и его свойства, понятие арифметического корня.
Степень положительного числа (13 часов)
Понятие степени с рациональным показателем, свойства степени с рациональным показателем. Понятие о пределе последовательности. Теоремы о пределах последовательностей. Существование предела монотонной и ограниченной. Ряды, бесконечная геометрическая прогрессия и ее сумма. Число e. Понятие степени с иррациональным показателем. Преобразование выражений, содержащих возведение в степень. Показательная функция, ее свойства и график.
Логарифмы (6 часов).
Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени, переход к новому основанию. Десятичный и натуральный логарифмы. Преобразование выражений, содержащих логарифмы.
Логарифмическая функция, ее свойства и график.
Простейшие показательные и логарифмические уравнения и неравенства методы их решения (11 часов).
Показательные и логарифмические уравнения и неравенства и методы их решения.
Синус и косинус угла и числа (7часов).
Радианная мера угла. Синус, косинус, тангенс и котангенс произвольного угла и действительного числа. Основное тригонометрическое тождество для синуса и косинуса. Понятия арксинуса, арккосинуса.
Тангенс и котангенс угла и числа (6 часов).
Тангенс и котангенс угла и числа. Основные тригонометрические тождества для тангенса и котангенса. Понятие арктангенса и арккотангенса.
Формулы сложения (11 часов).
Синус, косинус и тангенс суммы и разности двух аргументов. Формулы приведения. Синус и косинус двойного аргумента. Формулы половинного аргумента. Преобразование суммы тригонометрических функций в произведения и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразование тригонометрических выражений.
Тригонометрические функции числового аргумента (9 часов).
Тригонометрические функции, их свойства и графики, периодичность, основной период.
Тригонометрические уравнения и неравенства (12 часов).
Решение простейших тригонометрических уравнений и неравеств. Основные способы решения уравнений. Решение тригонометрических неравеств.
Вероятность события(6 часа).Частота. Условная вероятность (2 часа)
Табличное и графическое представление данных. Числовые характеристики рядов данных.
Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события.
Повторение курса алгебры и математического анализа за 10 класс (19 часов).
Средства контроля
Для проведения контрольных и самостоятельных работ, тестов, зачетов используется дидактический материал «Алгебра и начала математического анализа» для 10 класса, - М. Просвещение, 2009, М.К. Потапов, А.В. Шевкин, тематические тесты «Алгебра и начала математического анализа» для 10 класса, - М. Просвещение, 2009, Ю.В. Шепелева
Формы контроля: наблюдение, беседа, фронтальный опрос, опрос в парах, практикум, тесты, зачеты, самостоятельные и контрольные работы.
| Виды контроля | Количество часов |
| в год | 1 четверть | 2четверть | 3четверть | 4четверть |
| Контрольные работы |
|
|
|
|
|
| Самостоятельные работы |
|
|
|
|
|
| Тесты |
|
|
|
|
|
| Зачеты |
|
|
|
|
|
Учебно-методические средства обучения
Основная литература
Учебник «Алгебра и начала математического анализа» для 10 класса образовательных учреждений, - М. Просвещение, 2009, С. М. Никольский, М.К. Потапов, Н.Н. Решетников и др.
Дидактический материал «Алгебра и начала математического анализа» для 10 класса, - М. Просвещение, 2009, М.К. Потапов, А.В. Шевкин.
3.Методические рекомендации
4. Тематические тесты «Алгебра и начала математического анализа» для 10 класса, - М. Просвещение, 2009, Ю.В. Шепелева
Дополнительная литература
Журнал «Математика в школе».
Газета «1 сентября».
Дидактические материалы по алгебре и началам анализа 10-11 кл. Б. Г. Зив, П. И. Алтынов. Москва «Просвещение» 2001г.
«Алгебраический тренажёр» А. Г. Мерзляк и др. Москва «Илекса» 2007г.
«Готовимся к экзаменам по математике» П. Ф. Севрюков и др. Москва «Илекса» 2008г.
«Задачник по математике» Р. Б. Райхмист. Москва «Московский лицей» 2006г.
7. Белошистая А.В Математика: Тематическое планирование уроков подготовки к экзамену: Анализ тем и заданий, Тематическое планирование уроков подготовки к ЕГЭ, Подробный план каждого урока и др. - М: Экзамен, 2007г.(Серия ЕГЭ 2007)
8. Некрасов В.Б., Гущин Д.Д., Жигулев Л.А. Математика: Учебно-справочное пособие. Серия «Готовимся к ЕГЭ – 2008» - М.Просвещение, 2008
9. Единый государственный экзамен: Контрольно-измерительные материалы по математике: 2008-2009 (Серия единый государственный экзамен)– М.Просвещение, 2009
10. Денищева Л.О., Глазков Ю.А. Краснянская К.А. и др. Единый государственный экзамен: Математика: Методика подготовки. (Серия единый государственный экзамен) – М.Просвещение, 2009
11. Денищева Л.О., Михеева Т.Ф., Карюхина Н.В. Учимся решать уравнения и неравенства. 10-11 кл.- изд. Интеллект-Центр, 2007
12. Иванов М.А., Математика без репетитора: 800 задач с ответами и решениями для абитуриентов.- М.: Вентана-Графф, 2002.
13. Клово А.Г., Калашников В.Ю. и др. Пособие для подготовки к Единому государственному экзамену по математике, М. Центр тестирования МО РФ: 2010
14. Лысенко Ф.Ф., Калашников В.Ю., Неймарк А.Б., Давыдов Б.Е. Математика. Подготовка к ЕГЭ, подготовка к вступительным экзаменам.- Ростов-на-дону: Сфинск. 2004г, 2005г
15. Математика. Контрольно-измерительные материалы единого государственного экзамена в 2010 г. М.: Центр тестирования Минобразования России, 2010
16. Рязановский А.Р., Мирошин В.В. Готовимся к ЕГЭ. Математика. Решение задач повышенной сложности. - изд. Интеллект-Центр, 2007
17. Тематические тесты. Математика. ЕГЭ -2010г. / под ред. Ф.Ф.Лысенко – изд. Легион, Ростов-на-Дону, 2007г., 256с (пособие для самостоятельной подготовки учащихся)
18. Учебно-тренировочные материалы для подготовки учащихся. ЕГЭ-2010. Математика. изд. Интеллект-Центр, 2007
19. Учебно-тренировачные материалы для подготовки к ЕГЭ. Математика / Денищева Л.О., Глазков Ю.А., Краснянская К.А. и др. – М.: «Интеллект-Центр», 2010
повторения)
20. Журнал «Математика для школьников» (подписной индекс 80866)
1 Помимо указанных в данном разделе знаний, в требования к уровню подготовки включаются и знания, необходимые для применения перечисленных ниже умений.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Рабочая программа по учебному курсу «Алгебра и начала математического анализа» (10 классы) (0.29 MB)
Рабочая программа по учебному курсу «Алгебра и начала математического анализа» (10 классы) (0.29 MB)
 1
1 434
434 31
31 Нравится
0
Нравится
0


