Пояснительная записка
Рабочая программа по алгебре для 7 класса разработана в соответствии с Федеральными государственными образовательными стандартами основного общего образования 2-го поколения, Фундаментального ядра содержания общего образования и Требований к результатам основного общего образования, представленных в Федеральном государственном стандарте общего образования второго поколения; а также на основе авторской программы А.Г. Мордковича.
При составлении программы были использованы:
Ч.1. Учебник для учащихся общеобразовательных учреждений/ А.Г.Мордкович.-13-е изд., испр.- М.: Мнемозина,2009.-160с.
Ч.2.Задачник для учащихся общеобразовательных учреждений/А.Г.Мордкович.-13-е изд., испр.- М.:Мнемозина,2009.-164с
Программы: Математика.5-6 классы. Алгебра.7-9 классы. Алгебра и начала математического анализа. 10-11 классы/ авт.- сост. И.И.Зубарева, А.Г.Мордкович.- 2 изд., испр. и доп.- М.: Мнемозина, 2009.-63с.
Предметные знания и умения, приобретённые при изучении алгебры в 7 классе являются фундаментом обучения в старших классах. В то же время этот предмет является основой развития у учащихся познавательных действий, в первую очередь логических, включая и знаково-символические, а также таких, как планирование (цепочки действий по задачам), систематизация и структурирование знаний, преобразование информации, моделирование, дифференциация существенных и несущественных условий, аксиоматика, формирование элементов системного мышления, выработка вычислительных навыков. Особое значение имеет алгебра для формирования общего приема решения задач как универсального учебного действия. Таким образом, алгебра является эффективным средством развития личности школьника
Изучение алгебры в 7 классе направлено на достижение цели: формирование культурного человека, умеющего мыслить, понимающего идеологию математического моделирования реальных процессов, владеющего математическим языком не как языком общения, а как языком, организующим деятельность, умеющего самостоятельно добывать информацию и пользоваться ею на практике, владеющего литературной речью и умеющего в случае необходимости построить ее по законам математической речи.
Задачи:
содействовать овладению системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуально развивать формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
формировать представления об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитывать отношение к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса; волевых качеств; коммуникабельности; ответственности.
Общая характеристика учебного предмета.
В курсе алгебры можно выделить следующие основные содержательные линии: арифметика, алгебра, функции, вероятность и статистика. Содержание каждого из этих разделов разворачивается в содержательно- методическую линию, пронизывающую все основные содержательные линии. При этом первая линия - «Логика и множества» - служит цели овладения учащимися некоторыми элементами универсального математического языка, вторая - «Математика в историческом развитии» - способствует созданию общекультурного, гуманитарного фона изучения курса. Содержание линии «Алгебра» способствует формированию у учащихся математического аппарата для решения задач из разделов математики, смежных предметов и окружающей реальности. Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого раздела способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.
Курс имеет следующую структуру:
Математический язык. Математическая модель, Линейная функция, Системы двух линейных уравнений с двумя переменными, Степень с натуральным показателем и её свойства, Одночлены. Операции над одночленами, Многочлены. Арифметические операции над многочленами, Разложение многочленов на множители, Функция у = х2
Итоговое повторение.
Место предмета в учебном плане.
В соответствии с образовательной программой школы на 2015-2016 учебный год на изучение алгебры в 7 классе отводится 3 часа в неделю, всего – 102 часа + 3 часа резервных, что соответствует примерной программе по предмету «Алгебра» основного общего образования и Федеральному базисному учебному плану для образовательных учреждений РФ. Планируется в I четверти - 45 часа, во II - 35, в III - 50, в IV -45. Программа рассчитана на один год
Ценностные ориентиры содержания учебного предмета.
Сознательное овладение учащимися системой алгебраических знаний и умений необходимо в повседневной жизни для изучения смежных дисциплин и продолжения образования. Практическая значимость школьного курса алгебры обусловлена тем, что её объектом являются количественные отношения действительного мира. Математическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С её помощью моделируются и изучаются явления и процессы, происходящие в природе. Алгебра является одним из опорных предметов основной школы: она обеспечивает изучение предметов естественно - научного цикла.
Развитие логического мышления учащихся при обучении алгебры способствует усвоению предметов гуманитарного цикла. Требуя от учащихся умственных и волевых усилий, концентрации внимания, активности развитого воображения, алгебра развивает нравственные черты личности ( настойчивость, целеустремлённость, творческую активность, самостоятельность, дисциплину и критичность мышления) и умение аргументировано отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения.
Образовательные технологий и приемы, основные формы организации образовательного процесса для достижения образовательных результатов
Основная форма организации образовательного процесса – классно-урочная система.
В программе используются педагогические технологии:
технология коммуникативного обучения – направлена на формирование коммуникативной компетентности учащихся, которая является базовой, необходимой для адаптации к современным условиям межкультурной коммуникации.
технология разноуровневого (дифференцированного) обучения – предполагает осуществление познавательной деятельности учащихся с учётом их индивидуальных способностей, возможностей и интересов, поощряя их реализовывать свой творческий потенциал. Создание и использование диагностических тестов является неотъемлемой частью данной технологии.
технология индивидуализации обучения – помогает реализовывать личностно-ориентированный подход, учитывая индивидуальные особенности и потребности учащихся.
технология тестирования – используется для контроля уровня знаний на определённом этапе обучения. Осуществление контроля с использованием технологии тестирования соответствует требованиям всех международных экзаменов по математике. Кроме того, данная технология позволяет преподавателю выявить и систематизировать аспекты, требующие дополнительной проработки.
технология обучения в сотрудничестве – реализует идею взаимного обучения, осуществляя как индивидуальную, так и коллективную ответственность за решение учебных задач.
Комплексное использование в учебном процессе всех вышеназванных технологий стимулируют личностную, интеллектуальную активность, развивают познавательные процессы, способствуют формированию компетенций, которыми должен обладать учащийся основной школы.
При изучении курса используются формы обучения: фронтальная, индивидуальная, групповая.
Методы обучения: объяснительно-иллюстративные, проблемные (проблемные задачи, познавательные задачи и т.д.); частично-поисковые, методы организации и осуществления учебно-познавательной деятельности; методы стимулирования и мотивации учебно-познавательной деятельности; методы контроля и самоконтроля эффективности учебно-познавательной деятельности, методы изучения новых знаний, методы закрепления знаний, метод целесообразных задач, методы контроля, демонстрация, иллюстрация, схема, показ материала, график.
Результаты образования, способы и формы оценки достижения этих результатов:
В результате изучения курса алгебры, обучающиеся должны знать:
математический язык;
свойства степени с натуральным показателем;
определение одночлена и многочлена, операции над одночленами и многочленами;
формулы сокращенного умножения;
способы разложения на множители;
линейную функцию, её свойства и график;
квадратичную функцию и её график;
способы решения системы двух линейных уравнений с двумя переменными;
должны уметь:
составлять математическую модель при решении задач;
выполнять действия над степенями с натуральными показателями, показателем, не равным нулю, используя свойства степеней;
выполнять арифметические операции над одночленами и многочленами, раскладывать многочлены на множители, используя метод вынесения общего множителя за скобки, метод группировки, формулы сокращенного умножения;
строить графики линейной и квадратичной функций;
решать системы двух линейных уравнений с двумя переменными;
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения
обладать базовыми компетенциями: использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: для построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин; для выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; интерпретация графиков реальных зависимостей между величинами; для совершенствования навыков по использованию справочного материала и простейших вычислительных устройств.
Виды и формы контроля: фронтальная устная проверка, индивидуальный устный опрос, письменный контроль (контрольные и практические работы, тестирование, письменный зачет, тесты).
Содержание учебного предмета.
Математический язык. Математическая модель (13 ч)
Числовые и алгебраические выражения. Переменная. Допустимое значение переменной. Недопустимое значение переменной. Первые представления о математическом языке и о математической модели. Линейные уравнения с одной переменной. Линейные уравнения как математические модели реальных ситуаций. Координатная прямая, виды промежутков на ней.
Линейная функция (11 ч)
Координатная плоскость. Алгоритм отыскания координат точки. Алгоритм построения точки М (а; b) в прямоугольной системе координат.
Линейное уравнение с двумя переменными. Решение уравнения ах + by + с = 0. График уравнения. Алгоритм построения графика уравнения ах + by + с = 0.
Линейная функция. Независимая переменная (аргумент). Зависимая переменная. График линейной функции. Наибольшее и наименьшее значения линейной функции на заданном промежутке. Возрастание и убывание линейной функции.
Линейная функция у = kx и ее график.
Взаимное расположение графиков линейных функций.
Системы двух линейных уравнений с двумя переменными (13 ч)
Система уравнений. Решение системы уравнений. Графический метод решения системы уравнений. Метод подстановки. Метод алгебраического сложения.
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи).
Степень с натуральным показателем и её свойства (7 ч)
Степень. Основание степени. Показатель степени. Свойства степени с натуральным показателем. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем.
Одночлены. Операции над одночленами (8 ч)
Одночлен. Коэффициент одночлена. Стандартный вид одночлена. Подобные одночлены.
Сложение одночленов. Умножение одночленов. Возведение одночлена в натуральную степень. Деление одночлена на одночлен.
Многочлены. Арифметические операции над многочленами (15 ч)
Многочлен. Члены многочлена. Двучлен. Трехчлен. Приведение подобных членов многочлена. Стандартный вид многочлена.
Сложение и вычитание многочленов. Умножение многочлена на одночлен. Умножение многочлена на многочлен.
Квадрат суммы и квадрат разности. Разность квадратов. Разность кубов и сумма кубов.
Деление многочлена на одночлен.
Разложение многочленов на множители (18 ч)
Вынесение общего множителя за скобки. Способ группировки. Разложение многочлена на множители с помощью формул сокращенного умножения, комбинации различных приемов. Метод выделения полного квадрата.
Понятие алгебраической дроби. Сокращение алгебраической дроби.
Тождество. Тождественно равные выражения. Тождественные преобразования.
Функция у = х2 (8 ч)
Функция у = х2, ее свойства и график. Функция у = - х2, ее свойства и график.
Графическое решение уравнений. Кусочная функция. Чтение графика функции. Область определения функции. Первое представление о непрерывных функциях. Точка разрыва. Разъяснение смысла записи у = f(x). Функциональная символика.
Итоговое повторение (9 ч)
В разделе «Математический язык. Математическая модель» рассматривается понятие значения алгебраического выражения, допустимых значений переменных в алгебраическом выражении, даётся представление о математическом языке и терминологии, о математической модели, рассматривается решение текстовых задач с помощью уравнений.
В разделе «Линейная функция» вводится понятие уравнения с двумя переменными, их решении и графике уравнения, рассматривается линейная функция и её график, а также взаимное расположение графиков линейных функций.
В разделе «Системы двух линейных уравнений с двумя переменными» рассматриваются основные методы решения систем двух линейных уравнений с двумя переменными, а также решение текстовых задач с помощью систем уравнений.
В разделе «Степень с натуральным показателем и её свойства» рассматривается применение свойств степени в преобразованиях выражений, в вычислениях.
В разделе «Одночлены. Операции над одночленами» рассматриваются операции сложения и вычитания одночленов, умножения и возведения одночленов в степень.
В разделе «Многочлены. Арифметические операции над многочленами» рассматривается сумма и разность многочленов, произведение многочлена и одночлена, произведение многочленов, изучаются формулы сокращённого умножения и их применение в преобразованиях.
разделе «Разложение многочленов на множители» рассматриваются способы разложения многочленов на множители и применение разложения многочленов на множители.
В разделе «Функция у = х2 Место для формулы.« изучается функция у = , её свойства и график, рассматриваются кусочные функции.
В разделе «Итоговое повторение» » предусматривается повторение курса алгебры 7 класса.
| №п\п | Изучаемый материал | Кол-во часов |
|
| Глава 1.Математический язык. Математическая модель. | 16 |
| 1 | Числовые и алгебраические выражения. | 3 |
| 2 | Что такое математический язык. | 2 |
| 3 | Что такое математическая модель. | 3 |
| 4 | Входная контрольная работа | 1 |
| 5 | Линейное уравнение с одной переменной. | 2 |
| 6 | Координатная прямая. | 2 |
|
| Глава 2. Линейная функция. | 11 |
| 7 | Координатная плоскость. | 2 |
| 8 | Линейное уравнение с двумя переменными и его график. | 3 |
| 9 | Линейная функция и её график. | 3 |
| 10 | Линейная функция у=кх. | 1 |
| 11 | Взаимное расположение графиков линейных функций. | 1 |
| 12 | Контрольная работа №2.Линейная функция. | 1 |
|
| Глава3.Системы двух линейных уравнений с двумя переменными. | 13 |
| 13 | Основные понятия. | 2 |
| 14 | Метод подстановки. | 3 |
| 15 | Метод алгебраического сложения. | 3 |
| 16 | Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций. | 4 |
| 17 | Контрольная работа №3.Системы линейных уравнений с двумя переменными. | 1 |
|
| Глава 4.Степень с натуральным показателем и её свойства. | 7 |
| 18 | Что такое степень с натуральным показателем. | 1 |
| 19 | Таблица основных степеней. | 1 |
| 20 | Свойства степени с натуральным показателем. | 2 |
| 21 | Контрольная работа за 1 полугодие. | 1 |
| 22 | Умножение и деление степеней с одинаковым показателем. | 1 |
| 23 | Степень с нулевым показателем. | 1 |
|
| Глава 5.Одночлены. Операции с одночленами. | 8 |
| 24 | Понятие одночлена. Стандартный вид одночлена. | 1 |
| 25 | Сложение и вычитание одночленов. | 2 |
| 26 | Умножение одночленов. Возведение одночленов в натуральную степень. | 2 |
| 27 | Деление одночлена на одночлен. | 2 |
| 28 | Контрольная работа№5.Одночлены.Операции над одночленами. | 1 |
|
| Глава 6. Многочлены. Операции над многочленами. | 14 |
| 29 | Основные понятия. | 1 |
| 30 | Сложение и вычитание многочленов. | 2 |
| 31 | Умножение многочлена на одночлен. | 2 |
| 32 | Умножение многочлена на многочлен. | 3 |
| 33 | Формулы сокращенного умножения. | 5 |
| 34 | Деление многочлена на одночлен. | 1 |
| 35 | Контрольная работа №6.Многочлены. Операции над многочленами. | 1 |
|
| Глава 7 Разложение многочленов на множители. | 19 |
| 36 | Что такое разложение многочленов на множители и зачем оно нужно. | 1 |
| 37 | Вынесение общего множителя за скобки. | 2 |
| 38 | Способ группировки. | 2 |
| 39 | Разложение многочленов на множители с помощью формул сокращенного умножения. | 5 |
| 40 | Пробный РЭ. | 2 |
| 41 | Разложение многочленов на множители с помощью комбинации различных приёмов. | 3 |
| 42 | Сокращение алгебраических дробей. | 3 |
| 43 | Тождества. | 1 |
|
| Глава8. Функция у=х2. | 11 |
| 44 | Функция у=х2 и её график. | 3 |
| 45 | Графическое решение уравнений. | 2 |
| 46 | Что означает в математике запись у=f(х). | 3 |
|
| Глава9. Итоговое повторение. | 8 |
| 47 | Региональный экзамен. | 2 |
Итого: 105 ч + 2 ч РЭ.
Личностные, метапредметные и предметные результаты освоения учебного предмета.
В направлении личностного развития:
Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
Формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
Формирование качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
Формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
Развитие интереса к математическому творчеству и математических способностей;
В метапредметном направлении:
Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
Развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
В предметном направлении:
Овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, для изучения смежных дисциплин, применения в повседневной жизни;
Создание фундамента математического развития, формирования механизмов мышления, характерных для математической деятельности.
решать системы двух линейных уравнений с двумя переменными;
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения.
обладать базовыми компетенциями: использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: для построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин; для выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; интерпретация графиков реальных зависимостей между величинами; для совершенствования навыков по использованию справочного материала и простейших вычислительных устройств.
График проведения контрольных работ.
1. Контрольный срез №1 (Входная контрольная работа). 15.09.
2.Контрольная работа № 1: Математический язык. Математическая модель.3.10
3.Контрольная работа №2: Линейная функция 24.10
4. Контрольная работа №3: Системы линейных уравнений с двумя переменными.5.12
5. Контрольный срез №2 (Контрольная работа за 1 полугодие по математике).15.12.
6.Контрольная работа№5: Одночлены. Операции над одночленами.21.01
7.Контрольная работа №6: Многочлены. Операции над многочленами.25.02
8. Пробный РЭ по математике. 15.03.
9. Контрольная работа №8: Разложение многочленов на множители. 15.04.
10. Контрольная работа №9: Функция y=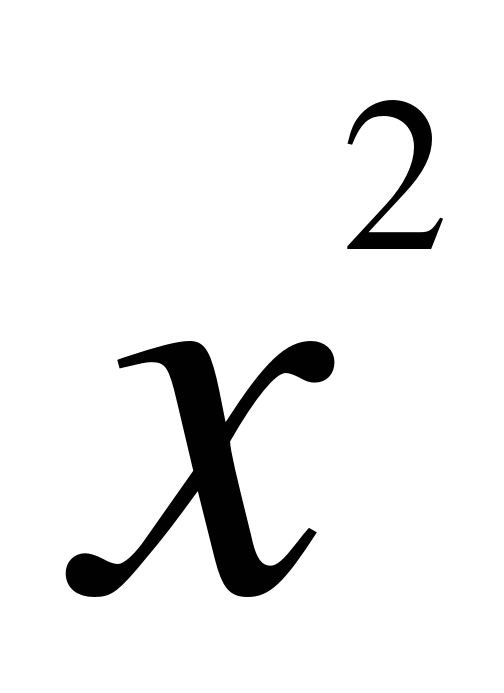
. 13.05.
11.Региональный экзамен по математике. 24.05.
Календарно-тематическое планирование с определением основных видов учебной деятельности обучающихся (приложение 1)
Описание материально-технического обеспечения образовательного процесса.
Магнитная доска, чертёжные инструменты, раздаточные карточки, таблицы, проектор, экран.
Список литературы.
Литература использованная при составлении программы:
Программа общеобразовательных учреждений. «Математика.5-6 классы. Алгебра.7-9 классы. Алгебра и начала математического анализа. 10-11 классы» / авт.- сост.И.И.Зубарева, А.Г.Мордкович.- 2 изд.,испр. и доп.- М.: Мнемозина, 2009.-63с.
Учебник: Алгебра. 7 класс. В 2 ч.
Ч.1. Учебник для учащихся общеобразовательных учреждений/ А.Г.Мордкович.-13-е изд., испр.- М.: Мнемозина,2009.-160с.
Ч.2.Задачник для учащихся общеобразовательных учреждений/А.Г.Мордкович.-13-е изд.,испр.- М.:Мнемозина,2009.-164с
Л.А. Александрова. Алгебра. 7класс. Контрольные работыдля учащихся общеобразовательных учреждений / . Под ред. А.Г. Мордковича.- М.: Мнемозина, 2009. 39 с.
Список литературы для учителя:
Программа общеобразовательных учреждений. «Математика.5-6 классы. Алгебра.7-9 классы. Алгебра и начала математического анализа. 10-11 классы» / авт.- сост.И.И.Зубарева, А.Г.Мордкович.- 2 изд.,испр. и доп.- М.: Мнемозина, 2009.-63с.
Учебник: Алгебра. 7 класс. В 2 ч.
Ч.1. Учебник для учащихся общеобразовательных учреждений/ А.Г.Мордкович.-13-е изд., испр.- М.: Мнемозина,2009.-160с.
Ч.2.Задачник для учащихся общеобразовательных учреждений/А.Г.Мордкович.-13-е изд.,испр.- М.:Мнемозина,2009.-164с
Л.А. Александрова. Алгебра. 7класс. Контрольные работы для учащихся общеобразовательных учреждений / . Под ред. А.Г. Мордковича.- М.: Мнемозина, 2009. 39 с.
Л.А. Александрова. Алгебра. 7класс. Самостоятельные работы для учащихся общеобразовательных учреждений / под ред. А.Г. Мордковича.- М.: Мнемозина, 2008.- 104 с.
Е.Е. Тульчинская. Алгебра – 7. Блицопрос. Пособие для учащихся.М.: Мнемозина, 2008.- 128 с.
А.Г. Мордкович, Е.Е. Тульчинская. Алгебра, 7 – 9. Тесты.
П.И. Алтынов. Дидактические материалы. Алгебра. Устные упражнения и диктанты. 7 -9 класс. Учебно-методическое пособие.
А.Г. Мордкович. Алгебра. 7 класс: Методическое пособие для учителя.М.: Мнемозина, 2008.-64 с.
Рурукин А. Н. Поурочные разработки по алгебре: 7 класс.- М.: ВАКО, 2010.-256 с.
Список литературы для учащихся:
Учебник: Алгебра. 7 класс. В 2 ч.
Ч.1. Учебник для учащихся общеобразовательных учреждений/ А.Г.Мордкович.-13-е изд., испр.- М.: Мнемозина,2009.-160с.
Ч.2.Задачник для учащихся общеобразовательных учреждений/А.Г.Мордкович.-13-е изд.,испр.- М.:Мнемозина,2009.-164с.
Л.А. Александрова. Алгебра. 7класс. Самостоятельные работы для учащихся общеобразовательных учреждений / под ред. А.Г. Мордковича.- М.: Мнемозина, 2008.- 104 с.
Приложение 2.
Критерии и нормы оценки знаний, умений и навыков обучающихся
1. Оценка письменных контрольных работ обучающихся.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Получите свидетельство
Вход
Рабочая программа по алгебре (для 7 класса) (0.15 MB)
0
543
32
Нравится
0
