Муниципальное автономное общеобразовательное учреждение
«Средняя общеобразовательная школа №33 с углубленным изучением отдельных предметов»
| РАССМОТРЕНА на заседании МО учителей математики, физики, информатики и ИКТ Протокол от_________ 2014 г. № _______ | СОГЛАСОВАНА заместитель директора по УВР МАОУ «СОШ № 33 с
углубленным изучением отдельных предметов» ________ (Н.В. Литке) (подпись) « » _________2014 г. | РАССМОТРЕНА на заседании педагогического совета. Протокол от _____________2014 г. № _______ | УТВЕРЖДЕНА приказом МАОУ «СОШ №33 с углубленным изучением отдельных предметов» от ____________ 2014г.
№ _______ |
РАБОЧАЯ ПРОГРАММА
по учебному предмету
«Алгебра»
7-9 класс (базовый уровень)
Разработчик:
Провоторова Елена Викторовна,
учитель математики
г. Старый Оскол
2014г.
Пояснительная записка
Рабочая программа по учебному предмету «Алгебра» для 7-9 классов разработана на основе авторской программы «Программа по алгебре», опубликованной в сборнике « Программы общеобразовательных учреждений. Алгебра. 7-9 классы. / Т.А. Бурмистрова. – М.: Просвещение, 2010
Цель программы: развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и др.), усвоение аппарата уравнений как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников.
Задачи программы:
формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов; овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно-научных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, алгоритмической культуры, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.
Так как авторская программа рассчитана на 34 учебные недели, а в учебном плане МАОУ «СОШ № 33 с углубленным изучением отдельных предметов» в 7, 8 классах 35 учебных недель, то в программу внесены изменения: добавлено 3 часа в раздел «Повторение» в 7 классе в конце года, а в 8 классе - в начале учебного года.
Для реализации Рабочей программы используется учебно-методический комплект, включающий:
7 класс
1. Алгебра. Учебник для 7 класса общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. - М.: Просвещение, 2010.
2.Алгебра. Дидактические материалы. 7 класс/ Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова. – М.: Просвещение, 2010.
8 класс
1. Алгебра. Учебник для 8 класса общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешкова, C. Б. Суворова. - М.: Просвещение, 2010.
2. Алгебра. Дидактические материалы. 8 класс / В.И. Жохов, Ю. Н. Макарычев, Н.Г. Миндюк. –М.: - Просвещение, 2012
9 класс
1. Алгебра. Учебник для 9 класса общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешкова, C. Б. Суворова. - М.: Просвещение, 2010.
2. Алгебра. Дидактические материалы. 9 класс / Ю. Н. Макарычев, Н.Г. Миндю, Л.Б. Крайнева. –М.: - Просвещение, 2012.
Рабочая программа рассчитана:
7 класс
Всего 123 часа. Текущий контроль знаний, умений и навыков проводится в виде 11 контрольных работ и 3 самотоятельных работ, 2 тестов, 1 итоговый тест.
8 класс
Всего 105 часов. Текущий контроль знаний, умений и навыков проводится в виде 11 контрольных работ и 3 самотоятельных работ, 2 тестов, 1 итоговый тест.
9 класс
Всего 102 часа. Текущий контроль знаний, умений и навыков проводится в виде 9 контрольных работ и 5 самотоятельных работ, 2 тестов.
Виды текущего контроля: устные (устный ответ на поставленный вопрос, развернутый ответ по заданной теме, устное сообщение по избранной теме, зачет по теме ); письменные (письменное выполнение тренировочных упражнений, выполнение самостоятельной работы, письменной проверочной работы, контрольной работы, тестов.); выполнение заданий с использованием ИКТ (компьютерное тестирование, on-line тестирование с использованием Интернет-ресурсов или электронных учебников, выполнение интерактивных заданий).
Форма организации учебного процесса - урок: урок-лекция, урок-исследование, урок-игра, комбинированный урок, урок решения задач, урок-контрольная работа. Формы контроля, используемые на уроках: индивидуальный, групповой, фронтальный. Методы контроля: устный опрос, контрольная работа, тестирование, самостоятельная работа.
Требования к уровню подготовки учащихся
7класс
В результате изучения курса алгебры учащиеся должны знать/уметь
Выражения, тождества, уравнения
правила сложения, умножения, деления отрицательных чисел с разными знаками; способы сравнения числовых и буквенных выражений; формулировки свойств действий над числами; определение тождества и тождественные преобразования выражений ; определения уравнения, корни уравнения, равносильные уравнения; определение линейного уравнения с одной переменной; алгоритм решения задач с помощью составления уравнений; определение среднего арифметического, размаха и моды упорядоченного ряда чисел; определение медианы как статистической характеристики; складывать, вычитать, умножать и делить десятичные и обыкновенные дроби; находить значение выражения при заданных значениях переменных; сравнивать выражения; читать и записывать неравенства и двойные неравенства; применять свойства действий над числами для преобразования выражений; приводить подобные слагаемые, раскрывать скобки, упрощать выражения, используя тождественные преобразования; расширять и обобщать знания о выражениях и их преобразованиях, предвидеть возможные последствия своих действий; находить корни уравнения (или доказывать, что их нет); решать линейные уравнения с одной переменной; решать уравнения вида ох = b и ох = 0; решать задачи с помощью линейных уравнений с одной переменной; находить среднее арифметической, размах и моду упорядоченного ряда чисел; находить медиану упорядоченного ряда чисел.
Функции
определение функции; определение графика; понятие прямой пропорциональности, коэффициента пропорциональности, углового коэффициента, устанавливать функциональную зависимость; находить значение функции по формуле, находить область определения функции;
находить значение аргумента, используя формулу; по графику находить значение функции или аргумента; по данным таблицы строить график зависимости величин; читать графики функции, строить графики функций; находить коэффициент пропорциональности, строить график функции у = kх; строить график прямой пропорциональности; определять знак углового коэффициента по графику; находить значение функции при заданном значении аргумента, находить значение аргумента при заданном значении функции; строить график линейной функции; по графику находить значения k и b; расширять и обобщать значения о построении графика линейной функции, исследовать взаимное расположение графиков линейных функций;
строить графики функций у = kх и у = kх + b.
Степень с натуральным показателем
понятия: степень, основание степени, показатель степени; правила умножения и деления степеней с одинаковыми основаниями; правила возведения в степень произведения; понятия: одночлен, коэффициент одночлена, стандартный вид одночлена; алгоритм умножения одночленов и возведение одночлена в натуральную степень; понятия: парабола, ветви параболы, ось симметрии параболы, вершина параболы; возводить числа в степень; заполнять и оформлять таблицы, отвечать на вопросы с помощью таблиц; применять свойства степеней для упрощения числовых и алгебраических выражений; умножать и делить степени с одинаковыми основаниями; возводить степень в степень; применять правила возведения в степень произведения; находить значение одночлена при указанных значениях переменных;
применять правила умножения одночленов, возведения одночлена в степень для упрощения выражений; строить параболу; описывать геометрические свойства кубической параболы;
находить значение функции у = х2 на заданном отрезке; находить точки пересечения параболы с графиком линейной функции.
Многочлены
правила умножения одночлена на многочлен; разложение многочлена на множители с помощью вынесения общего множителя за скобки; правило умножения многочлена на многочлен; способ группировки для разложения многочлена на множители; находить значение многочлена и определять степень многочлена; приводить подобные слагаемые; складывать и вычитать многочлены; представлять выражение в виде суммы или разности многочленов; умножать одночлен на многочлен, решать уравнения и задачи с помощью уравнений; раскладывать многочлен на множители способом вынесения общего множителя за скобки; умножать многочлен на многочлен, применять правило умножения многочленов; доказывать тождества и делимость выражений на число; раскладывать многочлен на множители способом группировки; применять способ группировки при разложении многочлена на множители; раскладывать на множители квадратный трёхчлен способом группировки.
Формулы сокращенного умножения
формулу квадрата суммы и квадрата разности двух выражений; формулу куба суммы и квадрата разности двух выражений; формулу разности квадратов двух выражений; формулу суммы и разности кубов двух выражений; определение целого выражения; способы разложения многочлена на множители. применять формулы квадрата суммы и квадрата разности; применять формулы для разложения трехчлена на множители; преобразовывать выражения в квадрат суммы; применять формулу умножения разности двух выражений на их сумму; раскладывать разность квадратов на множители; применять формулы сокращенного умножения; умножать, складывать, возводить в степень многочлены; применять различные способы для разложения многочлена на множители; преобразовывать целые выражения различными способами.
Системы линейных уравнений
определение линейного уравнения с двумя переменными и их решения; определение графика уравнения и графика линейного уравнения с двумя переменными; алгоритм решения системы линейных уравнений методом подстановки; алгоритм решения системы линейных уравнений методом алгебраического сложения; находить пары решений уравнения с двумя переменными; выражать одну переменную через другую; строить графики линейного уравнения с двумя переменными; находить решение системы с двумя переменными; графически решать системы линейных уравнений и выяснять, сколько решений имеет система уравнений; решать системы двух линейных уравнений методом подстановки; решать системы двух линейных уравнений методом алгебраического сложения; решать текстовые задачи с помощью систем линейных уравнений; решать текстовые задачи с помощью систем линейных уравнений на движение по дороге и воде; решать текстовые задачи с помощью систем линейных уравнений на части, на числовые величины и на проценты.
8 класс
Рациональные дроби
Знать основное свойство дроби, рациональные, целые, дробные выражения; правильно употреблять термины «выражение», «тождественное преобразование», понимать формулировку заданий: упростить выражение, разложить на множители, привести к общему знаменателю, сократить дробь. Знать и понимать формулировку заданий: упростить выражение, разложить на множители, привести к общему знаменателю, сократить дробь, свойства обратной пропорциональности. Уметь осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления, выполнять действия сложения и вычитания с алгебраическими дробями, сокращать дробь, выполнять разложение многочлена на множители применением формул сокращенного умножения, выполнять преобразование рациональных выражений. Уметь осуществлять в рациональных выражениях числовые подстановки и выполнять соответствующие вычисления, выполнять действия умножения и деления с алгебраическими дробями, возводить дробь в степень, выполнять преобразование рациональных выражений; правильно употреблять функциональную терминологию (значение функции, аргумент, график функции), строить график обратной пропорциональности, находить значения функции y=k/x по графику, по формуле.
Квадратные корни
Понятие об иррациональном числе. Общие сведения о действительных числах. Квадратный корень, приближённое значение квадратного корня. Свойства квадратных корней; преобразования выражений, содержащих квадратные корни. Функция и её график. Знать определения квадратного корня, арифметического квадратного корня, какие числа называются рациональными, иррациональными, как обозначается множество рациональных чисел; свойства арифметического квадратного корня. Уметь выполнять преобразование числовых выражений, содержащих квадратные корни; решать уравнения вида x2=а; находить приближенные значения квадратного корня; находить квадратный корень из произведения, дроби, степени, строить график функции и находить значения этой функции по графику или по формуле; выносить множитель из-под знака корня, вносить множитель под знак корня; выполнять преобразование выражений, содержащих квадратные корни.
Квадратные уравнения
Квадратное уравнение. Формулы корней квадратного уравнения. Теорема Виета. Решение рациональных уравнений. Решение задач, приводящих к квадратным и рациональным уравнениям. Знать, что такое квадратное уравнение, неполное квадратное уравнение, приведенное квадратное уравнение; формулы дискриминанта и корней квадратного уравнения, терему Виета и обратную ей; какие уравнения называются дробно-рациональными, какие бывают способы решения уравнений, понимать, что уравнение – это математический аппарат решения разнообразных задач математики, смежных областей знаний, практики. Уметь решать квадратные уравнения выделением квадрата двучлена, решать квадратные уравнения по формуле, решать неполные квадратные уравнения, решать квадратные уравнения с помощью теоремы, обратной теореме Виета, использовать теорему Виета для нахождения коэффициентов и свободного члена квадратного уравнения; решать текстовые задачи с помощью квадратных уравнений; решать дробно-рациональные уравнения, решать уравнения графическим способом, решать текстовые задачи с помощью дробно-рациональных уравнений.
Неравенства
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Применение свойств неравенств к оценке значения выражения. Линейное неравенство с одной переменной. Система линейных неравенств с одной переменной. Знать определение числового неравенства с одной переменной, что называется решением неравенства с одной переменной, что значит решить неравенство, свойства числовых неравенств, понимать формулировку задачи «решить неравенство». Уметь записывать и читать числовые промежутки, изображать их на числовой прямой, решать линейные неравенства с одной переменной, решать системы неравенств с одной переменной; применять свойства неравенства при решении неравенств и их систем.
Степень с целым показателем
Степень с целым показателем и её свойства. Стандартный вид числа. Запись приближенных значений. Действия над приближенными значениями. Знать определение степени с целым и целым отрицательным показателем; свойства степени с целым показателями. Уметь выполнять действия со степенями с натуральным и целым показателями; записывать числа в стандартном виде, записывать приближенные значения чисел, выполнять действия над приближенными значениями.
Элементы статистики и теории вероятностей
Сбор и группировка статистических данных. Наглядное представление статистической информации
9 класс
Квадратичная функция
Функция. Возрастание и убывание функции. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Решение задач путем выделения квадрата двучлена из квадратного трехчлена. Функция y=ax2 + bx + с, её свойства, график. Простейшие преобразования графиков функций. Решение неравенств второй степени с одной переменной. [Решение рациональных неравенств методом интервалов.] Знать основные свойства функций, уметь находить промежутки знакопостоянства, возрастания, убывания функций; определение и свойства четной и нечетной функций; определение корня n- й степени, при каких значениях а имеет смысл выражение ; что степень с основанием, равным 0 определяется только для положительного дробного показателя и знать, что степени с дробным показателем не зависят от способа записи r в виде дроби; свойства степеней с рациональным показателем, уметь выполнять простейшие преобразования выражений, содержащих степени с дробным показателем; свойства степенной функции с натуральным показателем. Уметь: находить область определения и область значений функции, читать график функции; решать квадратные уравнения, определять знаки корней; выполнять разложение квадратного трехчлена на множители; строить график функции у=ах2 , выполнять простейшие преобразования графиков функций; строить график квадратичной функции, выполнять простейшие преобразования графиков функций; строить график квадратичной функции» находить по графику нули функции, промежутки, где функция принимает положительные и отрицательные значения; построить график функции y=ax2 и применять её свойства. Уметь построить график функции y=ax2 + bx + с и применять её свойства; находить токи пересечения графика Квадратичной функции с осями координат; разложить квадратный трёхчлен на множители; решать квадратное уравнение; решать квадратное неравенство алгебраическим способом; решать квадратное неравенство с помощью графика квадратичной функции; решать квадратное неравенство методом интервалов; находить множество значений квадратичной функции; решать неравенство ах2 +вх+с.≥0 на основе свойств квадратичной функции; четная и нечетная функции. Функция y=xn, Определение корня n-й степени; строить график функции у=хn; решать уравнения хn=а при: а) четных и б)нечетных значениях n; выполнять простейшие преобразования и вычисления выражений, содержащих корни, применяя изученные свойства арифметического корня n-й степени; выполнять преобразования выражений, содержащих степени с дробным показателем
Уравнения и неравенства с одной переменной
Целое уравнение и его корни. Решение уравнений третьей и четвертой степени с одним неизвестным с помощью разложения на множители и введения вспомогательной переменной. Решение систем, содержащих одно уравнение (неравенство) первой, а другое второй степени. Решение задач методом составления систем. Знать методы решения уравнений: разложением на множители; введением новой переменной; графическим способом. Уметь: решать целые уравнения методом введения новой переменной; решать системы 2 уравнений с 2 переменными графическим способом; решать уравнения с 2 переменными способом подстановки и сложения; решать задачи «на работу», «на движение» и другие составлением систем уравнений.
Уравнения и неравенства с двумя переменными
Уравнение с двумя переменными и его график. Уравнение окружности. Решение систем двух уравнений второй степени с двумя переменными. Знать методы решения уравнений: разложением на множители; введением новой переменной; графическим способом. Уметь: решать целые уравнения методом введения новой переменной; решать системы 2 уравнений с 2 переменными графическим способом; решать уравнения с 2 переменными способом подстановки и сложения; решать задачи «на работу», «на движение» и другие составлением систем уравнений.
Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы n первых членов прогрессии. Знать формулу n–го члена арифметической прогрессии, свойства членов арифметической прогрессии, способы задания арифметической прогрессии; какая последовательность является геометрической, уметь выявлять, является ли последовательность геометрической, если да, то находить q. Уметь: применять формулу суммы n –первых членов арифметической прогрессии при решении задач; вычислять любой член геометрической прогрессии по формуле, знать свойства членов геометрической прогрессии; применять формулу при решении стандартных задач; применять формулу S= при решении практических задач; находить разность арифметической прогрессии; находить сумму n первых членов арифметической прогрессии; находить любой член геометрической прогрессии; находить сумму n первых членов геометрической прогрессии; решать задачи.
Элементы статистики и теории вероятностей
Комбинаторные задачи. Перестановки, размещения, сочетания. Перестановки. Размещения. Сочетания Вероятность случайного события. Знать формулы числа перестановок, размещений, сочетаний и уметь пользоваться ими. Уметь пользоваться формулой комбинаторики при вычислении вероятностей
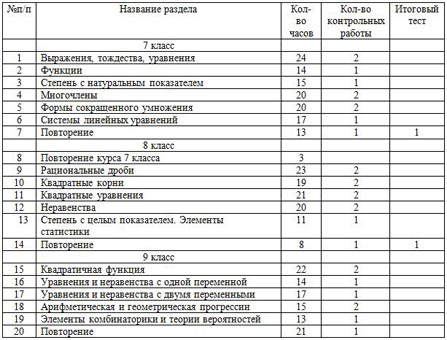
- Учебно-тематический план
| №п/п | Название раздела | Кол-во часов | Кол-во контрольных работы | Итоговый тест |
|
| 7 класс |
|
|
|
| 1 | Выражения, тождества, уравнения | 24 | 2 |
|
| 2 | Функции | 14 | 1 |
|
| 3 | Степень с натуральным показателем | 15 | 1 |
|
| 4 | Многочлены | 20 | 2 |
|
| 5 | Формы сокращенного умножения | 20 | 2 |
|
| 6 | Системы линейных уравнений | 17 | 1 |
|
| 7 | Повторение | 13 | 1 | 1 |
|
| 8 класс |
|
|
|
| 8 | Повторение курса 7 класса | 3 |
|
|
| 9 | Рациональные дроби | 23 | 2 |
|
| 10 | Квадратные корни | 19 | 2 |
|
| 11 | Квадратные уравнения | 21 | 2 |
|
| 12 | Неравенства | 20 | 2 |
|
| 13 | Степень с целым показателем. Элементы статистики | 11 | 1 |
|
| 14 | Повторение | 8 | 1 | 1 |
|
| 9 класс |
|
|
|
| 15 | Квадратичная функция | 22 | 2 |
|
| 16 | Уравнения и неравенства с одной переменной | 14 | 1 |
|
| 17 | Уравнения и неравенства с двумя переменными | 17 | 1 |
|
| 18 | Арифметическая и геометрическая прогрессии | 15 | 2 |
|
| 19 | Элементы комбинаторики и теории вероятностей | 13 | 1 |
|
| 20 | Повторение | 21 | 1 |
|
Формы и средства контроля
Для проведения контрольных и самостоятельных работ используются:
Дидактические материалы. Алгебра. 7 класс/ Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова. – М.: Просвещение, 2010.
Дидактические материалы. Алгебра. 8 класс / В.И. Жохов, Ю. Н. Макарычев, Н.Г. Миндюк. –М.: - Просвещение, 2012
Дидактические материалы. Алгебра. 9 класс / Ю. Н. Макарычев, Н.Г. Миндю, Л.Б. Крайнева. –М.: - Просвещение, 2012
Для проведения тестов - «Алгебра. 7-9 классы. Тематические тесты. Промежуточная аттестация», учебно-методическое пособие под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова. - Ростов-на-Дону: Легион-М, 2011
| № п/п | Виды проверочных работ |
Запланировано |
|
| 7 кл. | 8 кл. | 9 кл. |
| 1 | Контрольные работы | 11 | 11 | 9 |
| 2 | Тесты | 2 | 2 | 2 |
| 3 | Самостоятельные работы | 3 | 3 | 5 |
| 4 | Итоговый тест | 1 | 1 |
|
Критерии оценок по алгебре
Оценка устных ответов учащихся
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником,
изложил материал грамотным языком в определенной логической последовательности, точно
используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами,
применять их в новой ситуации при выполнении практического задания;
и устойчивость используемых при отработке умений и навыков;
при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по
замечанию учителя.
Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;
допущены один - два недочета при освещении основного содержания ответа, исправленные по замечанию учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.
Отметка «3» ставится в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, по показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»);
имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
Оценка письменных работ учащихся
Отметка «5» ставится, если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок; •S в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Отметка «1» ставится, если:
Оценка теста
«5» - 85% -100%
«4» - 51% - 84%
«3» - 35% - 50%
«2» - 0% - 34%
Перечень учебно-методических средств обучения
Основная литература
Изучение алгебры в 7-9 классах: пособие для учителей/ Ю.Н. Макарычев, Н.Г. Миндюк, С. Б. Суворова, И.С. Шлыкова. – М. Просвещение, 2009.
Алгебра. Учебник для 7 класса общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. - М.: Просвещение, 2010.
Алгебра. Дидактические материалы. 7 класс/ Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова. – М.: Просвещение, 2010.
Алгебра. Дидактические материалы. 8 класс / В.И. Жохов, Ю. Н. Макарычев, Н.Г. Миндюк. –М.: - Просвещение, 2012
Алгебра. Учебник для 9 класса общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешкова, C. Б. Суворова. - М.: Просвещение, 2010.
Алгебра. Учебник для 8 класса общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешкова, C. Б. Суворова. - М.: Просвещение, 2010.
Алгебра. Дидактические материалы. 9 класс / Ю. Н. Макарычев, Н.Г. Миндюк, Л.Б. Крайнева. –М.: - Просвещение, 2012
Дополнительная литература
Алгебра.: Поурочные планы по учебнику Ю.Н. Макарычева и др./ Л.А. Тапилина, Т.Л. Афанасьева. – Волгоград: Учитель, 2005.
Алгебра: 7-9 класс. Тематические тесты. Промежуточная аттестация/ Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова.- Ростов-на-Дону: Легион-М, 2011.
Самостоятельные и контрольные работы по алгебре и геометрии для 7-9 классов./Ершова А.П., Голобородько В.В., Ершова А.С. – М.: ИЛЕКСА, - 2009.
Оборудование и приборы
| № п/п | Наименование объектов и средств материально-технического обеспечения | Дидактическое описание | Количество |
| По плану | Фактически |
| 1. | Библиотечный фонд (книгопечатная продукция) |
| Стандарт основного общего образования по математике | Стандарт по математике, примерные программы, авторские программы входят в состав обязательного программно-методического обеспечения кабинета математики.
| 1 | 1 |
| Примерная программа основного общего образования по математике | 1 | 1 |
| Авторские программы по курсам математики | 1 | 1 |
| Учебник по алгебре для 7-9 классов | Комплекты учебников, рекомендованные (допущенные) к использованию в учебном процессе. | 100% | 100% |
| Дидактические материалы по алгебре для 7-9 классов | Входят в УМК, рекомендованные (допущенные к использованию в учебном процессе). | 100% | 100% |
| Научная, научно-популярная, историческая литература | Необходимы для подготовки докладов, сообщений, рефератов, творческих работ и должны содержаться в фондах библиотеки образовательного учреждения. | 7 | 7 |
| Справочные пособия (энциклопедии, словари, сборники основных формул и т.п.) | 7 | 7 |
| Методические пособия для учителя |
| 2 | 2 |
| 2. | Печатные пособия |
| Таблицы по алгебре | Служат для обеспечения наглядности при изучении материала, обобщения и повторения. Могут быть использованы при подготовке иллюстративного материала к докладу или реферату. | 11 | 11 |
| Портреты выдающихся деятелей математики | В демонстрационном варианте представлены портреты математиков, вклад которых в развитие математики представлен в стандарте. | 1 | 1 |
| 3. | информационно-коммуникативные средства |
| 3.1 | Мультимедийные обучающие программы и электронные учебные издания по основным разделам курса математики | Могут быть ориентированы на систему дистанционного обучения, либо носить проблемно-тематический характер и обеспечивать дополнительные условия для изучения отдельных тем и разделов стандарта. В любом случае они должны предоставлять техническую возможность построения системы текущего и итогового контроля уровня подготовки учащихся (в том числе, в форме тестового контроля). | 2 | 2 |
| 4. | Технические средства обучения1 |
| Мультимедийный компьютер |
| 1 | 1 |
| Мультимедиапроектор |
| 1 | 1 |
| Средства телекоммуникации | Включают: электронная почта, локальная сеть, выход в Интернет. | 1 | 1 |
| 5. | УЧЕБНО-ПРАКТИЧЕСКОЕ И УЧЕБНО-ЛАБОРАТОРНОЕ ОБОРУДОВАНИЕ |
| Комплект инструментов классных: линейка, транспортир, угольник (300, 600), угольник (450, 450), циркуль | Комплект предназначен для работы у доски. | 1 | 1 |

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по алгебре 7-9 классы (54.21 КB)
Рабочая программа по алгебре 7-9 классы (54.21 КB)
 0
0 4798
4798 1048
1048 Нравится
0
Нравится
0




