Муниципальное бюджетное образовательное учреждение
«Средняя общеобразовательная школа 15»
«Рассмотрено» «Согласовано» «Утверждаю»
на заседании методического заместитель директора по УР Директор МБОУ
«СОШ№15»
объединения учителей
математики и информатики
«_____»_________2013г «_____»__________2013г приказ № 595
Протокол №1 от « 01» 09. 2013г.
Руководитель МО
Рабочая программа
по алгебре
(базовый уровень)
для 10 класса
(к учебнику под редакцией А.Г.Мордкович)
Составитель: учитель математики
МБОУ «СОШ №15» г.Нижневартовска
Шарипова Н.Р.
2013 -2014 учебный год
Оглавление
1.Пояснительная записка 2
2.Учебно – тематический план 6
3.Содержание программы 9
4.Требования к уровню освоения содержания 12
5.Система диагностики. 15
6.Учебно-методическое обеспечение 18
7.МТБ дисциплины 19
8.Список литературы 20
Приложение 21
1.Пояснительная записка
Данная рабочая программа по математике для 10-11 классов (базовый уровень) реализуется на основе следующих документов:
1.Закона « Об образовании» Российской Федерации, Федерального компонента Государственного образовательного стандарта среднего (полного) общего образования по математике (алгебра и начала анализа), Устава МБОУ « СОШ №15», основной образовательной программой школы.
2. Примерной программы основного общего образования по алгебре и началам анализа, авторской программы по алгебре и началам анализа (автор А.Г.Мордкович).
Целью изучения курса алгебры и начал анализа в 10-11 классе является систематическое изучение функций как важнейшего математического объекта средствами алгебры и математического анализа, раскрытие политехнического и прикладного значения общих методов математики, связанных с исследованием функций, подготовка необходимого аппарата для изучения геометрии и физики.
Курс характеризуется содержательным раскрытием понятий, утверждений и методов, относящихся к началам анализа, выявлением их практической значимости. При изучении вопросов анализа широко используются наглядные соображения. Уровень строгости изложения определяется с учетом общеобразовательной направленности изучения начал анализа и согласуется с уровнем строгости приложений изучаемого материала в смежных дисциплинах. Характерной особенностью курса являются систематизация и обобщение знаний учащихся, закрепление и развитие умений и навыков, полученных в курсе алгебры, что осуществляется как при изучении нового материала, так и при проведении обобщающего повторения.
Учащиеся систематически изучают тригонометрические функции и их свойства, тождественные преобразования тригонометрических выражений и их применение к решению соответствующих уравнений и неравенств, знакомятся с основными понятиями, утверждениями, аппаратом математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие прикладные задачи.
Задачами среднего (полного) общего образования являются развитие интереса к познанию и творческих способностей обучающегося, формирование навыков самостоятельной учебной деятельности на основе дифференциации обучения. В дополнение к обязательным предметам вводятся предметы по выбору самих обучающихся в целях реализации интересов, способностей и возможностей личности.
Цель курса:
Изучение математики в старшей школе на базовом уровне направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
В рамках указанных содержательных линий решаются следующие задачи:
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
изучение свойств пространственных тел, формирование умения применять полученные знания для решения практических задач;
совершенствование интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления;
знакомство с основными идеями и методами математического анализа.
Общая характеристика учебного предмета.
создание условий для умения логически обосновывать суждения, выдвигать гипотезы и понимать необходимость их проверки;
создание условий для умения ясно, точно и грамотно выражать свои мысли в устной и письменной речи;
формирование умения использовать различные языки математики: словесный, символический, графический;
формирование умения свободно переходить с языка на язык для иллюстрации, интерпретации, аргументации и доказательства;
создание условий для плодотворного участия в работе в группе; умения самостоятельно и мотивированно организовывать свою деятельность;
формирование умения использовать приобретенные знания и умения в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных.
Огромная роль отводится использованию ИКТ - как основным современным средствам обучения, которые применяются в следующих видах:
- в использовании обучающих компьютерных программ, по которым учащиеся работают самостоятельно;
- в контроле и самоконтроле:
- в моделировании, обобщении изучаемого теоретического материала;
- в проектной, исследовательской деятельности.
Освоение содержания программы возможно с использованием внеурочных форм организации учебной деятельности:
учебная мастерская
творческая лаборатория
экскурсия;
интеллектуально-познавательная игра
интеллектуально-тематический вечер
викторина
конференции
встречи со специалистами ВУЗа
лекторий, семинар и т.п.
Для реализации рабочей программы предусмотрено использование дифференцированного подхода, через задания разного уровня сложности, обозначенные в учебнике специальными значками.
Методами обучения предмету являются: объяснительно-иллюстративный и репродуктивный, и частично-поисковый. На уроках используются элементы следующих технологий: личностно ориентированное обучение, обучение с применением компетентностно-ориентированных заданий, ИКТ.
Связь с остальными дисциплинами.
Наиболее тесные связи существуют между курсами математики и физики.
Огромное для физики имеют такие математические темы, как "Производная",
"Применения производной", "Интеграл и его применения".
С помощью методов математического анализа в значительной степени упрощаются решения многих физических задач.
Применение математической теории к решению прикладных задач - еще одно направление формирования мировоззрения учащихся о месте и роли математики в общественной практике людей. Через решение прикладных задач реализуется политехнический принцип обучения математике. Целенаправленное использование прикладных задач способствует ориентации учащихся на различные профессии, осуществлению связи обучения математике с жизнью.
Основные содержательные линии.
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», Вводится линия «Начала математического анализа». В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах
Сроки реализации 2012-2014 уч.г.
- 2.Учебно – тематический план
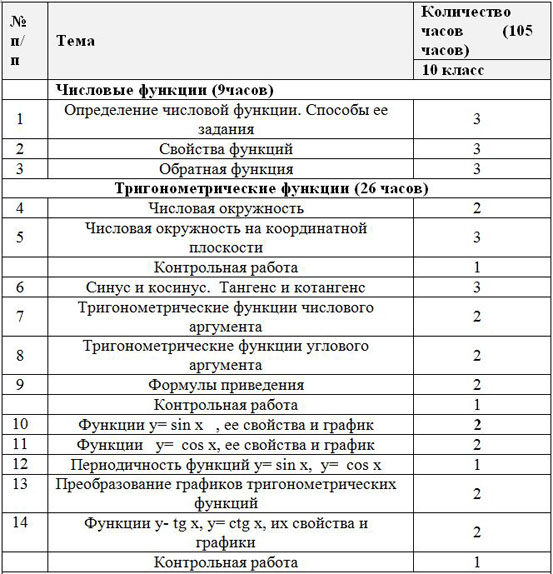
| № п/п | Тема | Количество часов (105 часов) |
| 10 класс |
|
| Числовые функции (9часов) |
| 1 | Определение числовой функции. Способы ее задания | 3 |
| 2 | Свойства функций | 3 |
| 3 | Обратная функция | 3 |
| Тригонометрические функции (26 часов) |
| 4 | Числовая окружность | 2 |
| 5 | Числовая окружность на координатной плоскости | 3 |
|
| Контрольная работа | 1 |
| 6 | Синус и косинус. Тангенс и котангенс | 3 |
| 7 | Тригонометрические функции числового аргумента | 2 |
| 8 | Тригонометрические функции углового аргумента | 2 |
| 9 | Формулы приведения | 2 |
|
| Контрольная работа | 1 |
| 10 | Функции у= sin x , ее свойства и график | 2 |
| 11 | Функции у= cos x, ее свойства и график | 2 |
| 12 | Периодичность функций у= sin x, у= cos x | 1 |
| 13 | Преобразование графиков тригонометрических функций | 2 |
| 14 | Функции у- tg x, у= ctg x, их свойства и графики | 2 |
|
| Контрольная работа | 1 |
| Тригонометрические уравнения (10) |
| 15 | Арккосинус и решение уравнений cos x=а | 2 |
| 16 | Арксинус и решение уравнений sin x=а | 2 |
| 17 | Арктангенс арккотангенс. Решение уравнений tg x=а, ctg x=а | 1 |
| 18 | Тригонометрические уравнения | 4 |
|
| Контрольная работа | 1 |
| Преобразование тригонометрических выражений( 15часов) |
| 19 | Синус и косинус суммы и разности аргументов | 4 |
| 20 | Тангенс суммы и разности аргументов | 2 |
| 21 | Формулы двойного угла | 3 |
| 22 | Преобразование суммы тригонометрических функций в произведение | 3 |
|
| Контрольная работа | 1 2 |
| 23 | Преобразование произведений тригонометрических функций в сумму |
| Производная(30часов) |
| 24 | Числовые последовательности и их свойства Предел числовой последовательности | 2 |
| 24 | 2 |
| 25 | Сумма бесконечной геометрической прогрессии | 2 |
| 26 | Предел функции | 3 |
| 27 | Определение производной | 3 |
| 28 | Вычисление производных | 3 |
|
| Контрольная работа | 1 |
| 29 | Уравнение касательной к графику функции | 2 |
| 30 | Применение производной для исследования функции | 2 |
| 31 | Построение графиков | 3 |
|
| Контрольная работа | 1 |
| 32 | Применение производной для отыскания наибольших и наименьших значений непрерывной функции на промежутке | 3 |
|
| Задачи на отыскание наибольшего и наименьшего значений величин | 3 |
|
| Контрольная работа | 2 |
|
| Обобщающее повторение | 15 |
| Итого 105 час |
| 11 класс Степени и корни. Степенные функции (18 часов) |
| 33 | Понятие корня п-й степени из действительного числа. | 2 |
| 34 | Функция у=√х , их свойства и график | 3 |
| 35 | Свойства корня п-й степени | 3 |
| 36 | Преобразование выражений содержащих радикалы | 3 |
|
| Контрольная работа | 1 |
| 37 | Обобщение понятия о показателе степени | 3 |
| 38 | Степенные функции, их свойства и графики | 3 |
| Показательная и логарифмическая функции(29 часов) |
| 39 | Показательная функция, ее свойства и график | 3 |
| 40 | Показательные уравнения Показательные неравенства | 4 |
|
| Контрольная работа | 1 |
| 41 | Понятие логарифма | 2 |
| 42
| Логарифмическая функция, ее свойства и график | 3 3 |
| 43 | Свойства логарифмов |
| 44 | Логарифмические уравнения | 3 |
|
| Контрольная работа | 1 |
| 45 | Логарифмические неравенства | 3 |
| 46 | Переход к новому основанию логарифма | 2 |
| 47 | Дифференцирование показательной и логарифмической функций | 3 |
|
| Контрольная работа | 1 |
| Первообразная и интеграл(8часов) |
| 48 | Первообразная и неопределенный интеграл | 3 |
| 49 | Определенный интеграл | 4 |
|
| Контрольная работа | 1 |
| Элементы математической статистик, комбинаторики и теории вероятностей (15часов) |
| 50 | Статистическая обработка данных | 3 |
| 51 | Простейшие вероятностные задачи | 3 |
| 52 | Сочетания и размещения | 3 |
| 53 | Формула бинома Ньютона | 2 |
| 54 | Случайные события и их вероятности | 3 |
|
| Контрольная работа | 1 |
| Уравнения и неравенства. Системы уравнений и неравенств (20 часов) |
| 55 | Равносильность уравнений | 2 |
| 56 | Общие методы решения уравнений | 3 |
| 57 | Решение неравенств с одной переменной | 4 |
| 58 | Уравнения и неравенства с двумя переменными | 2 |
| 59 | Системы уравнений | 4 |
| 60 | Задачи с параметрами | 3 |
|
| Контрольная работа | 2 |
|
| Обобщающее повторение | 15 |
|
| ИТОГО | 105( часов) |
3.Содержание программы
10 класс (105 часов)
Числовые функции (9 ч)
Определение функции, способы ее задания, свойства функций. Обратная функция.
Тригонометрические функции (26 ч)
Числовая окружность. Длина дуги единичной окружности. Числовая окружность на координатной плоскости. Синус и косинус. Тангенс и котангенс. Тригонометрические функции числового аргумента. Тригонометрические функции углового аргумента. Формулы приведения. Функция у = sin х, ее свойства и график. Функция у = cos х, ее свойства и график. Периодичность функций у = sin х, у = cos х. Построение графика функций у = mf(x) и у = f(kx) по известному графику функции у = f(x). Функции у = tg х л у = ctg х, их свойства и графики.
Тригонометрические уравнения (10 ч)
Первые представления о решении тригонометрических уравнений. Арккосинус. Решение уравнения cos t = а. Арксинус. Решение уравнения sin t = а. Арктангенс и арккотангенс. Решение уравнений tg х = a, ctg х = а.
Простейшие тригонометрические уравнения. Два метода решения тригонометрических уравнений: введение новой переменной и разложение на множители. Однородные тригонометрические уравнения.
Преобразование тригонометрических выражений (15 ч)
Синус и косинус суммы и разности аргументов. Формулы двойного аргумента. Формулы понижения степени. Преобразование сумм тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в суммы.
Производная (31 ч)
Определение числовой последовательности и способы ее задания. Свойства числовых последовательностей.
Определение предела последовательности. Свойства сходящихся последовательностей. Вычисление пределов последовательностей. Сумма бесконечной геометрической прогрессии.
Предел функции на бесконечности. Предел функции в точке. Приращение аргумента. Приращение функции.
Задачи, приводящие к понятию производной. Определение производной. Алгоритм отыскания производной. Формулы дифференцирования. Правила дифференцирования. Дифференцирование функции у = f(kx + т.).
Уравнение касательной к графику функции. Алгоритм составления уравнения касательной к графику функции у = f(x).
Применение производной для исследования функций на монотонность и экстремумы. Построение графиков функций. Применение производной для отыскания наибольших и наименьших значений величин.
Обобщающее повторение (14ч)
11 класс (105 ч)
Степени и корни. Степенные функции (18 ч)
Понятие корня л-й степени из действительного числа. Функции у = yfx, их свойства и графики. Свойства корня л-й степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики.
Показательная и логарифмическая функции (29 ч)
Показательная функция, ее свойства и график. Показательные уравнения. Показательные неравенства.
Понятие логарифма. Функция у = logax, ее свойства и график. Свойства логарифмов. Логарифмические уравнения. Логарифмические неравенства. Переход к новому основанию логарифма. Дифференцирование показательной и логарифмической функций.
Первообразная и интеграл (8 ч)
Первообразная. Правила отыскания первообразных. Таблица основных неопределенных интегралов.
Задачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла. Формула Ньютона — Лейбница. Вычисление площадей плоских фигур с помощью определенного интеграла.
Элементы математической статистики, комбинаторики и теории вероятностей (15 ч)
Статистическая обработка данных. Простейшие вероятностные задачи. Сочетания и размещения. Формула бинома Ньютона. Случайные события и их вероятности.
Уравнения и неравенства. Системы уравнений и неравенств (20 ч)
Равносильность уравнений. Общие методы решения уравнений: замена уравнения h(f(x)) = ft(g(x)) уравнением f(x) = g(x), разложение на множители, введение новой переменной, функционально-графический метод.
Решение неравенств с одной переменной. Равносильность неравенств, системы и совокупности неравенств, иррациональные неравенства, неравенства с модулями.
Системы уравнений. Уравнения и неравенства с параметрами.
Обобщающее повторение (15 часов)
- 4.Требования к уровню освоения содержания
Результаты обучения представлены в «Требованиях к уровню подготовки», задающих систему итоговых результатов обучения, которые должны быть достигнуты всеми учащимися, оканчивающими 10-11 классы, и достижение которых является обязательным условием положительной аттестации ученика за курс 10-11 классов. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни».
В результате изучения курса математики 10-11 классов обучающиеся должны:
Знать
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира.
Алгебра
Уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Начала математического анализа
уметь
вычислять производные и первообразные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
составлять уравнения и неравенства по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Элементы комбинаторики, статистики и теории вероятностей
уметь
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни, для анализа информации статистического характера: анализа реальных числовых данных, представленных в виде диаграмм, графиков;
- 5.Система диагностики.
Основными методами проверки знаний и умений учащихся по математике являются устный опрос и письменные работы. К письменным формам контроля относятся: математические диктанты, самостоятельные, проверочные (обучающего и контролирующего характера) и контрольные работы, тест.
Письменный контроль
Письменная проверка позволяет за короткое время проверить знания большого числа учащихся одновременно. Используется письменный контроль знаний учащихся в целях диагностики умения применять знания в учебной практике и осуществляется в виде диктантов, контрольных, проверочных и самостоятельных работ, тестов, рефератов.
1. Диктант
Диктант используется как форма опроса для контроля за усвоением проходимого материала, его обобщения и систематизации и выявления готовности учащихся к восприятию нового.
Диктант обычно проводится в самом начале урока, состоит из двух вариантов. Текст вопросов простой, легко воспринимаемый на слух, требующий краткого ответа, несложных вычислений. Пауза между следующими друг за другом вопросами должна быть достаточной для записи ответов учащимися.
2. Зачет
Зачет проводится для определения достижения конечных результатов обучения по определенной теме каждым учащимся. Перед началом изучения материала учащиеся знакомятся с перечнем вопросов и обязательных задач по теме, а также дополнительными вопросами и задачами. Иногда целесообразны закрытые зачеты, когда учащиеся получают вопросы и задания непосредственно во время проведения зачета. Его достоинство заключается в том, что он предполагает комплексную проверку всех знаний и умений учащихся.
Необходимость такого тематического контроля обусловлена тем, что для каждого ученика характерен определенный темп овладения учебным материалом. А потому обычные контрольные работы, в которых трудно учесть должным образом индивидуальные особенности учащихся, могут оказаться недостаточными для того, чтобы судить, достигнуты ли планируемые результаты обучения.
Зачет - это одна из основных форм контроля в старших классах.
Тематические зачеты должны быть дифференцированными, чтобы ученик мог самостоятельно выбрать уровень зачета. Учитель решает, основываясь на результатах прошлых или промежуточных контрольных мероприятий, какие знания и умения целесообразно проверять у какого ученика: всем даются индивидуальные задания. Ученик может решать задачи, потом делать лабораторную работу, а затем беседовать с учителем.
3. Самостоятельная работа
Традиционная форма контроля знаний, которая по своему назначению делится на обучающую самостоятельную работу и контролирующую. Самостоятельная работа творческого характера позволит не только проверить определенные знания, умения, но и развивать творческие способности учащихся.
Самостоятельная работа является необходимым этапом любой темы. Как правило, она проводится после коллективного решения или обсуждения задач новой темы и обязательно предшествует контрольной работе по этой теме. Работа выполняется без помощи учителя.
4. Контрольная работа
Контрольные работы проводятся с целью определения конечного результата в обучении по данной теме или разделу, контролировать знания одного и того же материала неоднократно. Целесообразно проводить контрольные работы различного вида.
С помощью промежуточной контрольной работы учитель проверяет усвоение учащимися материала в период изучения темы.
Итоговая контрольная работа проводится с целью проверки знаний и умений учащихся по отдельной теме, курсу.
Домашняя контрольная работа дается 1-2 раза в учебном году. Она призвана систематизировать знания, позволяет повторить и закрепить материал. При ее выполнении учащиеся не ограничены временем, могут использовать любые учебные пособия, проконсультироваться у учителя, родителей, одноклассников. Каждому ученику дается свой вариант работы, в который включаются творческие задания для формирования разносторонней развитой личности.
5. Практическая работа
Для закрепления теоретических знаний и отработки навыков и умений, способности применять знания при решении конкретных задач используется практическая работа, которая связана не только с заданием на компьютере, но и, например, может включать задания построения схемы, таблицы, написания программы и т. д.
6. Тест
Тест представляет собой кратковременное технически сравнительно просто составленное испытание, проводимое в равных для всех испытуемых условиях и имеющее вид такого задания, решение которого поддается качественному учету и служит показателем степени развития к данному моменту известной функции у данного испытуемого.
Система контролирующих материалов, позволяющих оценить уровень и качество ЗУН обучающихся на входном, текущем и итоговом этапах изучения предмета включает в себя сборники тестовых и текстовых заданий:
для 10 класса:
Алгебра и начала анализа. 10 кл.: Самостоятельные работы: Учеб. пособие для общеобразоват. учреждений / Л.А. Александрова; под ред. А.Г. Мордковича. – М.: Мнемозина, 2005. – 135 с.
Алгебра и начала анализа. 10 – 11 кл.: Контрольные работы для общеобразоват. учреждений: учеб. пособие / А.Г. Мордковича, Е.Е. Тульчинская. – 5-е изд. – М.: Мнемозина, 2007. – 62 с.
Алгебра и начала математического анализа. 10 класс. Контрольные работы для учащихся общеобразовательных учреждений (базовый уровень) / В.И. Глизбург; под ред. А.Г. Мордковича. – М.: Мнемозина, 2009. – 39 с.
Алгебра и начала анализа. 10 – 11 кл.: Тематические тесты и зачеты для общеобразоват. учреждений / Л.О. Денищева, Т.А Корешкова; под ред. А.Г. Мордковича. – 2-е изд., испр. и доп. – М.: Мнемозина, 2005. – 102 с.
Дидактические материалы по геометрии для 10 класса. / Б.Г. Зив – 10 изд. – М.: Просвещение, 2009г.
Геометрия. 10 класс. Рабочая тетрадь. Пособие для учащихся общеобразовательных учреждений. Базовый и профильный уровни. / Ю.А. Глазков, И.И. Юдина, В.Ф. Бутузов – 4 изд. – М.: Просвещение, 2010г.
для 11 класса:
Алгебра и начала анализа. 11 кл.: Самостоятельные работы: Учеб. пособие для общеобразоват. учреждений / Л.А. Александрова; под ред. А.Г. Мордковича. – 4-е изд., испр. и доп. – М.: Мнемозина, 2009. – 100 с.
Алгебра и начала анализа. 10 – 11 кл.: Контрольные работы для общеобразоват. учреждений: учеб. пособие / А.Г. Мордковича, Е.Е. Тульчинская. – 5-е изд. – М.: Мнемозина, 2007. – 62 с.
Алгебра и начала математического анализа. 11 класс. Контрольные работы для учащихся общеобразовательных учреждений (базовый уровень) / В.И. Глизбург; под ред. А.Г. Мордковича. – М.: Мнемозина, 2009. – 32 с.
Алгебра и начала анализа. 10 – 11 кл.: Тематические тесты и зачеты для общеобразоват. учреждений / Л.О. Денищева, Т.А Корешкова; под ред. А.Г. Мордковича. – 2-е изд., испр. и доп. – М.: Мнемозина, 2005. – 102 с.
Дидактические материалы по геометрии для 11 класса. / Б.Г. Зив – 9 изд. – М.: Просвещение, 2008г.
Геометрия. 11 класс. Рабочая тетрадь. Пособие для учащихся общеобразовательных учреждений. Базовый и профильный уровни. / Ю.А. Глазков, И.И. Юдина, В.Ф. Бутузов – 5 изд. – М.: Просвещение, 2010г.
6.Учебно-методическое обеспечение
| Наименование предмета | Основная литература (учебники) | Учебные и справочные пособия: | Учебно-методическая литература: | Медиаресурсы |
| Алгебра и начала анализа | 1. Математика. 10 класс: учеб. для общеобразоват. учреждений (базовый уровень) / [А.Г. Мордкович, И.М. Смирнова, и др.]; под ред. А.Г. Мордковича, И.М. Смирновой. – М.: Мнемозина, 2009. 2. Математика. 11 класс: учеб. для общеобразоват. учреждений (базовый уровень) / [А.Г. Мордкович, И.М. Смирнова, и др.]; под ред. А.Г. Мордковича, И.М. Смирновой. – М.: Мнемозина, 2009. | 1. Программы. Математика. 5 – 6 классы. Алгебра 7 – 9 классы. Алгебра и начала математического анализа. 10 – 11 классы / авт.-сост. И.И. Зубарева, А.Г. Мордкович. – 2-е изд., испр. и доп. – М.: Мнемозина, 2009. | 1. Алгебра и начала математического анализа. 10-11 классы (базовый уровень): методическое пособие для учителя / А.Г. Мордкович, П.В. Семенов. – М.: Мнемозина, 2010. | 1. Учебное пособие «Уроки алгебры Кирилла и Мефодия 10-11 классы» 2. Учебное пособие «1С: Математический конструктор 2.0» 3. Учебное пособие «Открытая математика. Алгебра» 4. Учебное пособие «Открытая математика. Функции и графики» |
7.МТБ дисциплины
(ИКТ оборудование)
Системный блок.
Монитор.
Мультимедиапроектор.
МФУ.
Документ-камера.
WEB-камера.
Доска антибликовая магнитная.
Интерактивное копиустройство.
Сплитер.
Колонки
Комплект учебных мультимедиа – продуктов к учебникам и задачникам А.Г.Мордковича «Алгебра.10-11классов»
- 8.Список литературы
Федеральный компонент государственного стандарта основного общего образования по математике / Сборник нормативных документов. Математика / сост. Э.Д. Днепров, А.Г. Аркадьев. – 2-е изд. стереотип. – М.: Дрофа, 2008. – 128 с.
Примерная программа основного общего образования по математике, рекомендованная Министерством образования и науки РФ / Сборник нормативных документов. Математика / сост. Э.Д. Днепров, А.Г. Аркадьев. – 2-е изд. стереотип. – М.: Дрофа, 2008. – 128 с.
Государственный образовательный стандарт общего образования / Официальные документы в образовании. – 2004. №24-25.
Закон Российской Федерации «Об образовании» / Образование в документах и комментариях. – М.: АСТ «Астрель» Профиздат. – 2005. 64 с.
Методические рекомендации по разработке и утверждению рабочих программ учебных дисциплин базисного учебного плана образовательного учреждения / – Издательство: Учебно-методический центр, г. Серпухов, 2008. – 10 с.
Приложение
Нормы оценки по основным формам контроля
Оценка письменных работ
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Оценка устных ответов учащихся
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
Oтвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
2

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по алгебре (10 класс) (0.19 MB)
Рабочая программа по алгебре (10 класс) (0.19 MB)
 0
0 749
749 71
71 Нравится
0
Нравится
0






