Конкурсное задание очного тура
муниципального этапа
«УЧИТЕЛЬ ГОДА-2016»
Открытый урок по алгебре и
началам математического анализа в 10-Б классе
МБОУ «Черноморская средняя школа №2
Черноморский район Республика Крым
по теме: «Показательная функция и ее свойства»
Рыбакова Рита Николаевна,
учитель математики МБОУ
«Черноморская средняя
школа №1»
Черноморский район
Республика Крым
Черноморское, 2015 учебный
Урок по алгебре и началам математического анализа
в 10 классе
УМК учебник “Алгебра и начала математического анализа 10 класс” С.М. Никольский, М.К. Потапов и др. Учебник для общеобразовательных организаций: базовый и углубленный уровни / -- М. : Просвещение, 2014.-431 с.:
Изучаемая тема: «Степень положительного числа» (§ 4).
Тема урока: «Показательная функция».
Место урока в изучаемой теме: первый.
Тип урока: комбинированный с применением компьютера и проектора .
Компьютерные технологии создают большие возможности активизации учебной деятельности. Широкое применение ИКТ при изучении большинства предметов дает возможность реализовать принцип “учение с увлечением”, и тогда любой предмет будет иметь равные шансы стать любимым детьми.
Технология: компьютерная, интерактивная использование элементов проектной деятельности.
Формы организации деятельности учащихся: фронтальная, групповая.
Метод: комбинированный (словесно-наглядно-практический).
Цели урока:
Предметные: изучение и первичное осознание нового учебного материала, сформировать у учащихся представление о показательной функции, ее свойствах и графиках, установить зависимость показательной функции от основания с помощью практической работы, познакомить учащихся с решением простейших неравенств использованием свойств показательной функции.
Личностные: формировать умение определять способы действий в рамках предложенных условий и требований, корректировать свои действия в связи с изменяющейся ситуацией.
Метапредметные: формировать умение видеть математическую задачу в контексте проблемной ситуации, в окружающей жизни.
Планируемые результаты: учащийся получит представление о показательной функции, ее видах, свойствах и графике, научится устанавливать зависимость и решать различные задания в зависимости от основания показательной функции
Основные понятия: Показательная функция, основные свойства, график показательной функции.
Задачи урока:
научить строить простейшие графики показательной функции и решать показательные уравнения графически,
научить применять свойства показательной функции,
осуществить контроль знаний,
использовать различные приемы и методы для поддержания работоспособности учащихся.
Материал для урока подобран таким образом, что предполагает работу учащихся различных категорий - от слабых учеников до сильных.
Личностные УУД: формировать учебную мотивацию, адекватную самооценку, необходимость приобретения новых знаний;
Познавательные УУД: формировать навыки построения графиков показательной функции, определения основных свойств функции, применения этих свойств в различных типах примеров.
Регулятивные УУД: понимать учебную задачу урока, осуществлять решение учебной задачи под руководством учителя, определять цель учебного задания, контролировать свои действия в процессе его выполнения, обнаруживать и исправлять ошибки, отвечать на итоговые вопросы и достижения;
Коммуникативные УУД: воспитывать любовь к математике, коллективизм, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность мышления.
Оборудование и материалы к уроку:
Доска, мультимедиапроектор,презентация, авторский «Электронный тренажер», раздаточный материал: вопросы для повторения и по новой теме, таблицы свойств, листы формата А4 с заранее начерченными координатными плоскостями, задачник.
Ход урока:
Ян Амос Каменский сказал: «Считай несчастным тот день или тот час, в котором, ты не усвоил ничего, ничего не прибавил к своему образованию».
Чешский педагог и гуманист
Сегодня каждый из вас унесёт с собой, что-то новое, неизвестное, интересное, познавательное. Мы с вами поговорим о применении отдельных вопросов математики, порешаем интересные задачи, узнаем интересные эпизоды из жизни великих математиков, и постараемся определить самого эрудированного математика.
Организационный
– создать положительную мотивацию к изучению материала
-- Создает эмоциональный настрой: Ребята,
Наш девиз сегодня на уроке: «Учение с увлечением»
Актуализация знаний («ориентирование»)
– повторить необходимые теоретические сведения
Задает вопросы:
Определение степени с рациональным и иррациональным показателем.
Свойства степени.
Таблица степеней.
Таблица квадратов.
Преобразования графиков функций.
Свойства функций.
Малая схема исследования функций и построение графика.
Графический способ решения уравнений.
Учащиеся отвечают на вопросы, отмечают то, что недостаточно усвоено, что необходимо еще повторить
УУД
Регулятивные: контроль, коррекция
Познавательные: поиск и выделение необходимой информации, структурирование знания
Коммуникативные: аргументирование своего мнения, умение корректно поправлять товарища
А для начала повторим преобразования графиков функций:
«Кто из вас уверен, что знает все преобразования и безошибочно их узнает? (вызываю учащихся, двоеборье)
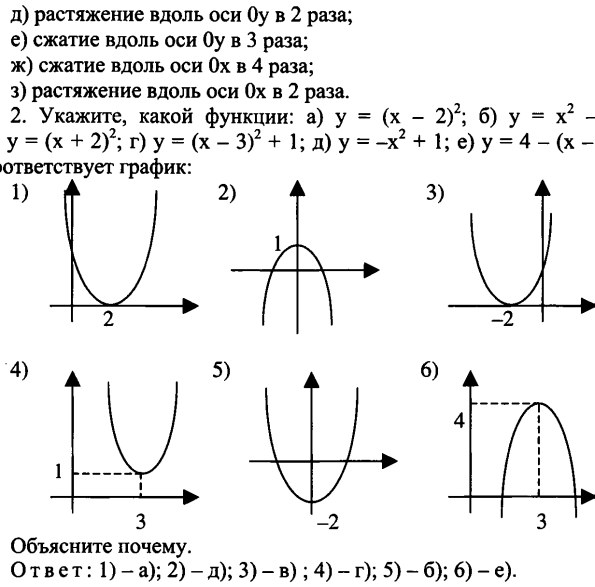
Звучит магнитная запись (приложение 1).
“22 ноября 2003 года в 10 часов 20 минут по московскому времени с космодрома “Плесецк” стартовал космический корабль “Русь–2”. Цель экспедиции: установить причины отсутствия связи с космической станцией “Русь–1”, работающей на планете Кармен. После стыковки космонавты обнаружили погибший экипаж станции. Капитан корабля, летчик-космонавт Игнатьев решил исследовать биосферу планеты. Исследования показали, что в верхнем слое грунта наблюдается необычайно быстрый рост числа колоний живых организмов (бактерий), что поставило под угрозу жизнь экипажа и грозит катастрофой планете. Как нормализовать ситуацию и предотвратить катастрофу?”
Итак, первая экспедиция погибла от неизвестных бактерий.
Ученые установили, что рост числа бактерий происходил по такой зависимости:
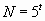, где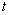 
– время размножения, 
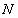– число колоний бактерий (приложение 2,сл №1).
Подсчитайте, как изменится число колоний бактерий за 2 секунды? (увеличится до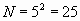 
). За 3 секунды? (увеличится до 
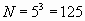) (слайд №2). Т.е. каждому моменту времени соответствует свое определенное число бактерий.
Я предлагаю вам исследовать эту зависимость. А к проблеме экспедиции мы вернемся в конце урока.
Зависимость между двумя переменными такого типа была замечена не только в процессе роста числа микроорганизмов, но и, например, в спорте – зависимость длины прыжка спортсмена с трамплина от начальной скорости полета, в медицине – способность почек выводить из крови радиоактивные изотопы, в предвыборных кампаниях. В рамках предвыборной кампании каждый кандидат выбирает себе в помощники двух доверенных лиц (слайд №3). Каждый из доверенных лиц в течение следующего дня, проводя агитационную работу, привлекает в команду этого кандидата еще по одному человеку. На следующий день агитационная работа проводится уже командой в 4 человека. Что произойдет с командой кандидата, если эту работу продолжить по той же схеме? Если эту работу продолжить, то команда кандидата будет очень быстро расти.
Для данного вида зависимостей ученые составили следующую математическую модель: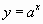 
(слайд №4).
Что представляет из себя правая часть формулы? (Степень).
Чему равно основание степени? (Основание равно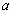 
).
А что такое х? (показатель степени)
Поэтому эту функцию назвали.… Как вы думаете, как? (Показательной функцией) А почему?
Именно потому, что аргумент находится в показателе степени, она носит название показательной функции.
Попробуйте сформулировать тему урока. (“Показательная функция”)
Эта функция обладает одним замечательным свойством: скорость роста пропорциональна значению самой функции. Она как костер, который, чем больше разгорается, тем больше в него надо подкладывать дров.
Изучением этой функции мы и займемся сегодня на уроке.
Что значит “Изучить функцию”? (Дать определение, сформулировать свойства и построить график)
Следовательно, целями урока являются…(сформулировать определение, рассмотреть свойства и построить график показательной функции). А поможет нам в достижении целей – составление опорного конспекта (см. приложение 3), который лежит перед вами на столах (слайд №5).
Запишите тему урока в опорном конспекте.
Планирование работы («план»)
– составить план работы
– перечень свойств, которые будут исследоваться;
Организует поисковую работу учащихся (по составлению плана действий), побуждает учащихся к высказыванию своего мнения.
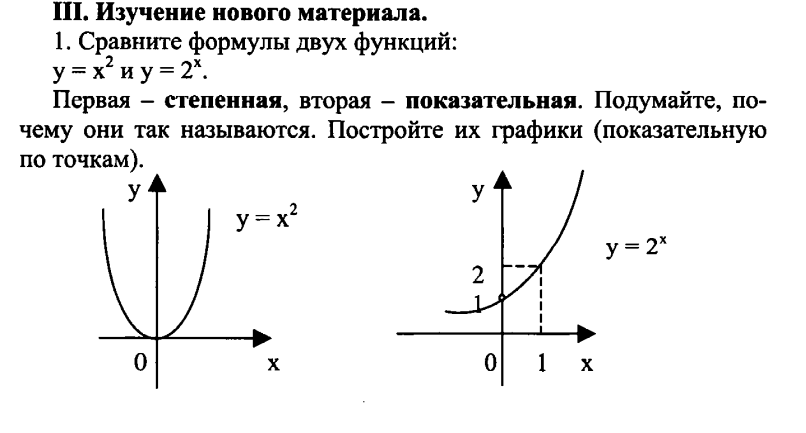
Практическая работа: В одной системе координат построить график показательной функции, если а=1/2.
На основании наблюдений сделать вывод о расположении графиков функций при а=2 и при а=1/2.
Если дана точка А (х;у), то в какую точку она переходит и назовите ее координаты.
Сделать выводы о свойствах функций в зависимости от оснований и заполнить таблицу:
| Свойства |
|
|
Область определения или существования |
|
|
Область значений функции, или область изменения |
|
|
Значения у для х=0 |
|
|
Значения у для х0 |
|
|
Значения у для х |
|
|
Промежутки монотонности |
|
|
Четность, нечетность |
|
|
Непрерывность |
|
|
Наибольшее и наименьшее значение функции |
|
|
Презентация Дарии Смолкотиной и Анастасии Наконечной, учащейся 11-М класса МБОУ «ЧСШ № 1»и д/з: Творческое задание + п.4.8, № 4.55(б,д,з); №4.57; № 4.60 (а,в,д,ж,и)
Проблема поставлена, вы понимаете, что далеко не все применения рассмотрены в презентации, и вы можете найти и предложить еще, а кто знает, может кому-то пригодится в жизни, в будущей профессии.
Повторяем план исследования свойств функции (приложение):
Электронный тренажер (рефлексия) -0 контроль полученных знаний.
Подведение итогов урока, выставление оценок
Некоторые наиболее часто встречающиеся виды функций, прежде всего показательные, открывают доступ ко многим исследованиям.
Л. Эйлер
Получите свидетельство
Вход
Конспект урока алгебры и начала математического анализа "Показательная функция" (0.44 MB)
0
1127
123
Нравится
0
