Применение производной к исследованию функции

Подготовка выпускников

к ЕГЭ

по математике

Загадка

1

2

ЕГЭ

3

4

5

Инструкция к применению

Цель:

Подготовиться к тестированию предметно и психологически

Правильная организация своей деятельности

1

Ориентировка в тексте

Часть В

5-6 простых, понятных, лёгких

2-3 понятных, но нужно что-то вспомнить

Часть С

1 можно решить без особого напряжения

Правильная организация своей деятельности

2

Ориентировка во времени

1 час - уйдёт на 7-8 заданий 1-ой части (что не успели, следует оставить).

2 час - на задания с 9 по 14 (этого достаточно на «4»)

3 час - посвятить 2-му разделу (1-2 задания)

4 час - вернуться к несделанному

цитата

«Знай, куда идёшь,

знай, зачем идёшь.

Если не знаешь, остановись и подумай.

Иногда полезнее вернуться».

Правильная организация своей деятельности

3

Выбор заданий

Исследование функции с помощью производной

В 14

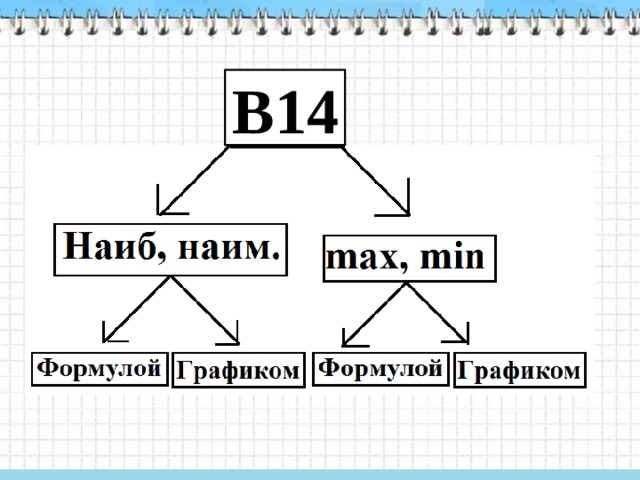
В14

Почему не выбрали?

Слабые места:

Советы:

Незнание формул производной

Избегать этих заданий

Ошибки в арифметических действиях

Отработать навыки решения до автоматизма

Неуверенное владение алгоритмом вычисления

Найти производную:

2x cos x – sin x

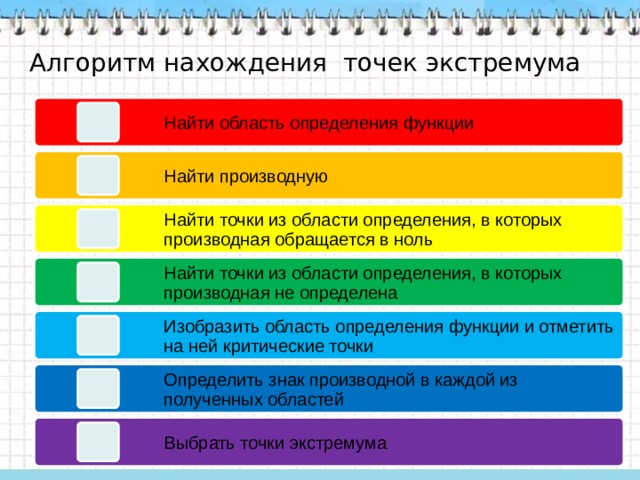
Алгоритм нахождения точек экстремума

Найти область определения функции

Найти производную

Найти точки из области определения, в которых производная обращается в ноль

Найти точки из области определения, в которых производная не определена

Изобразить область определения функции и отметить на ней критические точки

Определить знак производной в каждой из полученных областей

Выбрать точки экстремума

Примеры

Пусть теперь функция f имеет на отрезке [а; b] конечное число критических точек.

Наибольшее и наименьшее значения функция f может принимать в критических точках функции или в точках а и b.

Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.

наибольшее

значение

наименьшее

значение

c

a

b

наибольшее

значение

наибольшее

значение

http://www.terver.ru/maththeoryAlgebra.php

наименьшее

значение

наименьшее

значение

c

n

a

b

12

Этапы

Найдите наименьшее значение функции

1. Найти f / (x)

y = x 3 – 27x на отрезке [0; 4]

2. Найти критические точки, взять те, которые принадлежат данному отрезку.

3. Вычислить значения функции в критических точках и на концах отрезка.

4. Из вычисленных значений выбрать наименьшее или наибольшее

1) y / = 3x 2 – 27

-3

3

2) y / = 3x 2 – 27 = 3(x 2 – 9) = 3(x – 3)(x + 3)

[0; 4]

x = 3

[0; 4]

x = –3

3) y(0) = 0

y(4) = 4 3 – 27 4 = – 44

y(3) = 3 3 – 27 3 = –54

-

4

5

В 14

х

3

х

1

0

Этапы

Найдите наименьшее значение функции

1. Найти f / (x)

y = x 3 – 27x на отрезке [0; 4]

2. Найти критические точки, взять те, которые принадлежат данному отрезку.

3. Вычислить значения функции в критических точках

и на концах отрезка.

4. Из вычисленных значений выбрать наименьшее и наибольшее

1) y / = 3x 2 – 27

-3

3

2) y / = 3x 2 – 27 = 3(x 2 – 9) = 3(x – 3)(x + 3)

+

y \

+

–

4

0

y

x

-3

3

min

Наименьшее значение функция будет принимать в точке минимума.

Можно сэкономить на вычислениях значений функции в концах отрезка.

3)

y(3) = 3 3 – 27 3 = –54

-

4

5

В 14

х

3

х

1

0

Этот способ будет удобно

вспомнить, когда вычисления значений функции в концах отрезка будет сложным.

2.

Найдите наибольшее значение функции y = x 3 – 3x + 4

на отрезке [– 2; 0]

Значения функции в концах отрезка.

1) y(0) = 4

y(-2) = (-2) 3 – 3 (-2) +4 = 2

-1

1

2) y / = 3x 2 – 3 = 3(x 2 – 1) = 3(x – 1)(x + 1)

Найдем критические точки, которые принадлежат заданному отрезку.

[-2; 0]

x = 1

[-2; 0]

x = –1

Значения функции в критических точках, которые принадлежат заданному отрезку.

y(-1) = (-1) 3 – 3 (-1) + 4 = 6

6

Выбрать наибольшее из полученных значений.

В 14

х

3

х

1

0

min

min

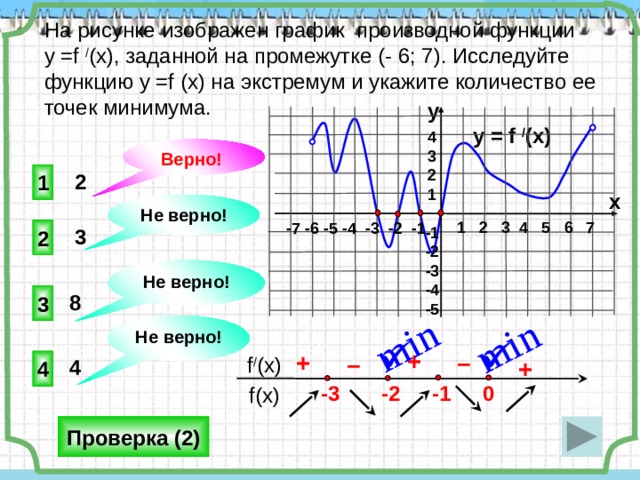
На рисунке изображен график производной функции

у =f / (x), заданной на промежутке (- 6; 7). Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума.

y

y = f / (x)

4

3

2

1

Верно!

1

2

x

Не верно!

1 2 3 4 5 6 7

-7 -6 -5 -4 -3 -2 -1

-1

-2

-3

-4

-5

2

3

Не верно!

8

3

Не верно!

+

–

+

–

f / (x)

+

4

4

-1

0

-3

-2

f(x)

Проверка (2)

max

max

max

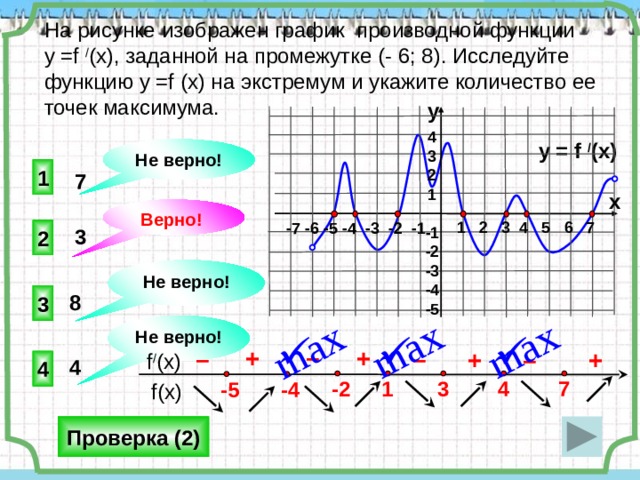
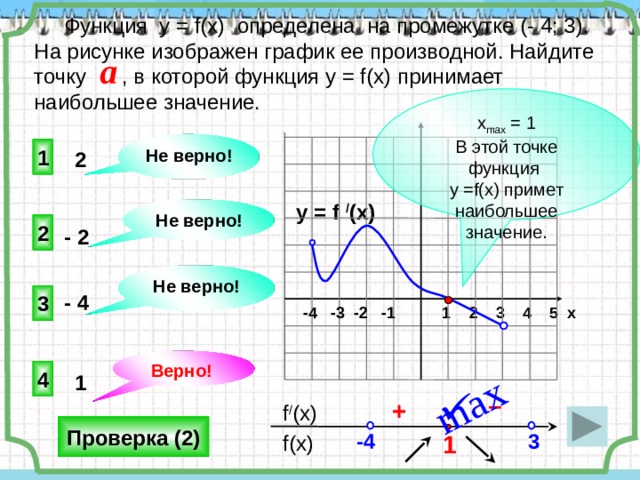
На рисунке изображен график производной функции

у =f / (x), заданной на промежутке (- 6; 8). Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек максимума.

y

4

3

2

1

y = f / (x)

Не верно!

1

7

x

Верно!

1 2 3 4 5 6 7

-7 -6 -5 -4 -3 -2 -1

-1

-2

-3

-4

-5

2

3

Не верно!

8

3

Не верно!

–

+

+

–

–

+

+

–

f / (x)

4

4

7

4

-2

1

3

-4

-5

f(x)

Проверка (2)

max

Функция у = f(x) определена на промежутке (- 4; 3). На рисунке изображен график ее производной. Найдите точку , в которой функция у = f(x) принимает наибольшее значение.

a

х max = 1

В этой точке функция

у =f(x) примет наибольшее значение.

Не верно!

1

2

y = f / (x)

Не верно!

2

- 2

Не верно!

- 4

3

-4 -3 -2 -1

1 2 3 4 5 х

Верно!

4

1

–

+

f / (x)

Проверка (2)

3

-4

1

f(x)

Правильная организация своей деятельности

4

Ориентировка в оформлении задания

-

4

3

х

В 14

3

х

1

0

9

-

,

5

В 14

х

3

х

1

0

2

4

0

х

В 14

3

х

1

0

-

,

5

4

7

В 14

х

3

х

1

0

Правильная организация своей деятельности

5

Полезные советы

Физминутка

Здравый смысл ответов

Гимнастика для глаз (моргание, зажмуривание, «по углам»)

Вращение головой

«Пальчики»

5

Инструкция к применению

1

Ориентировка в тексте

2

Ориентировка во времени

3

Цель:

Подготовиться к тестированию предметно и психологически

Выбор заданий

4

Ориентировка в оформлении задания

5

Полезные советы

Знания хорошие

по данной теме

Что-то осталось

непонятным

Плохо знаю

данную тему

Спасибо за урок!