Авторская программа элективного курса по математике «Решение задач повышенной сложности» 11 класс
Автор: Серебренникова Ирина Валентиновна
Пояснительная записка.
Целью данного курса математики является подготовка учащихся средней (полной) школы к Единому Государственному Экзамену, к продолжению образования, повышение уровня их математической культуры.
Преподавание строится как углубленное изучение вопросов, предусмотренных программой основного курса. Углубление реализуется на базе обучения методам и приемам решения математических задач, уровень которых не выходит за рамки основного курса, но уровень их трудности - повышенный, требующий применения учащимися знаний в нестандартной ситуации. Решение таких задач способствует:
- отработке теоретических знаний;
- развитию практических навыков решения задач;
- успешной подготовке к сдаче ЕГЭ;
- подготовке к продолжению образования в вузах.
Данная программа рассчитана на 34 часа, из них 6 часов отводится на теорию, 28 часов –
на практику. Предполагается 1 контрольная работа в конце прохождения курса.
Содержание рабочей программы.
1.Функции
Определение функции. Графики элементарных функций. Свойства функций. Чтение графиков функций. Преобразования графиков. Графическое решение уравнений, неравенств и их систем.
2. Иррациональные уравнения и неравенства.
Преобразования иррациональных выражений, освобождение от иррациональности. Равносильность уравнений и уравнения следствия. Решение иррациональных уравнений и неравенств. Решение систем иррациональных уравнений.
3. Производная.
Геометрический и механический смысл производной. Исследование функций на монотонность и экстремумы. Построение графиков функций. Решение задач на нахождение наибольшего и наименьшего значений функции.
4. Тригонометрия.
Преобразование тригонометрических выражений. Построение графиков тригонометрических функций. Графическое решение уравнений неравенств. Основные методы решения тригонометрических уравнений, отбор корней, запись решений. Решений тригонометрических неравенств.
5. Показательная и логарифмическая функции.
Определение, свойства и график показательной функции. Определение, свойства и график логарифмической функции. Преобразования показательных и логарифмических выражений. Основные методы решения показательных и логарифмических уравнений. Решения показательных и логарифмических неравенств, их систем. Сравнение чисел.
6. Геометрия.
Решение треугольников. Координаты и векторы в пространстве. Применение векторов к решению задач. Площади поверхностей. Объемы тел.
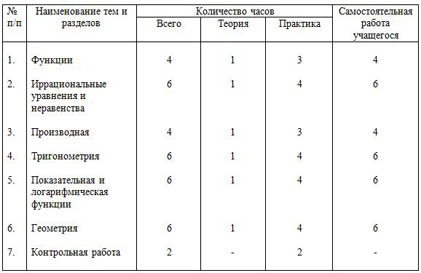
Учебно-тематический план.
| № п/п | Наименование тем и разделов | Количество часов | Самостоятельная работа учащегося |
| Всего | Теория | Практика |
|
1.
2.
3.
4.
5.
6.
7. |
Функции
Иррациональные уравнения и неравенства
Производная
Тригонометрия
Показательная и логарифмическая функции
Геометрия
Контрольная работа
|
4
6
4
6
6
6
2 |
1
1
1
1
1
1
-
|
3
4
3
4
4
4
2
|
4
6
4
6
6
6
-
|
Литература.
1. Сборник «100х4 задач» для поступающих в ВУЗы / В.К.Егерев; А.Г.Мордкович - М: Linka – Press, 1993
2. Сборник конкурсных задач для поступающих во ВТУЗы / М.И.Сканави Киев: Каннон, 1997
3. Задачи повышенной сложности начала анализа. Пособие для 10-11 классов / Б.М.Ивлев; А.М.Абрамов и др. – М: Просвещение, 1990
4. Факультативные занятия по геометрии для 7-11 классов / Л.М.Лоповок – Киев: Радянська школа, 1990
5. Практикум. Уравнения. Неравенства. Системы. 8-11 кл. / А.В.Бобровская, О.И.Чикунова ОГУП «Шадринский Дом Печати», 2013
6. Практикум. Стереометрия 10-11 кл. / А.В.Бобровская, О.И.Чикунова ОГУП «Шадринский Дом Печати», 2013
7. Учебно-тренировочные материалы для подготовки к единому государственному экзамену. Математика. М: Интеллект – центр, 2004
8. Алгебраический тренажер / А.Г.Мерзляк, В.Б.Полонский, М.С.Якир Киев: А.С.К., 1997
9. http://www.fipi.ru/ Открытый банк заданий
Контрольно – измерительный материал
Вариант 1.
1. Вычислите: 9 · log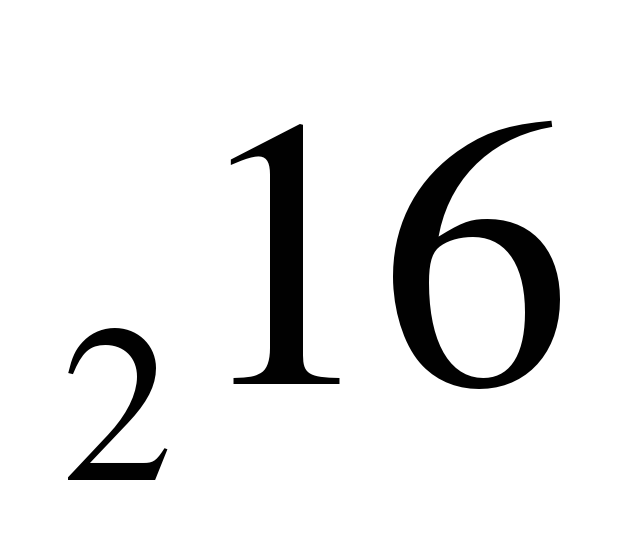 + 3
+ 3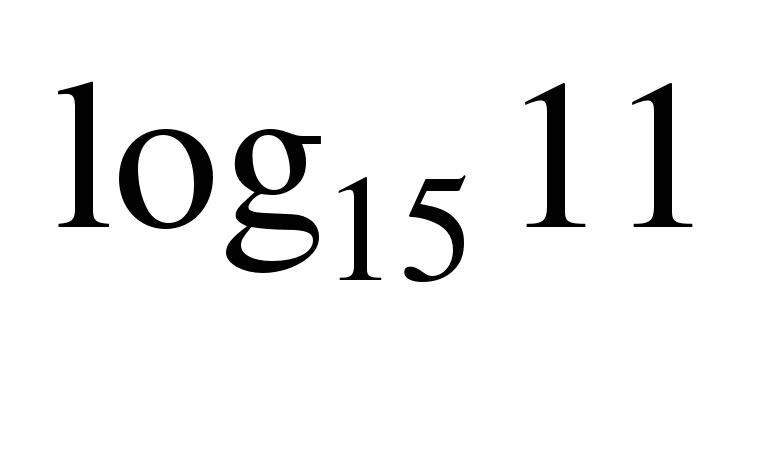 · 5
· 5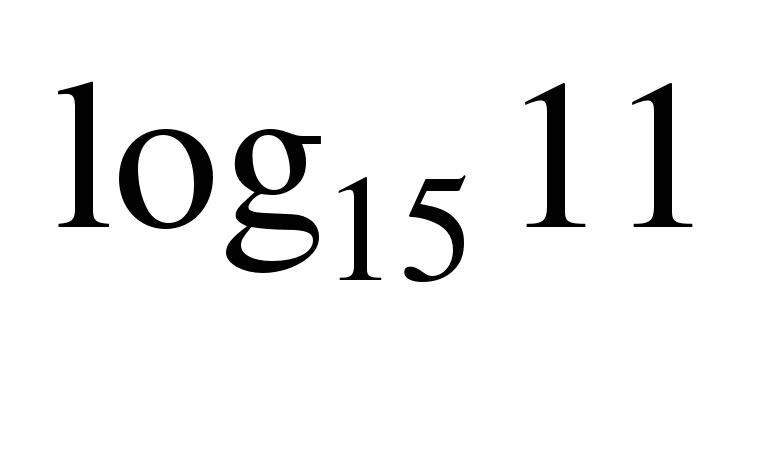 .
.
2. Найти наибольшее значение функции y = 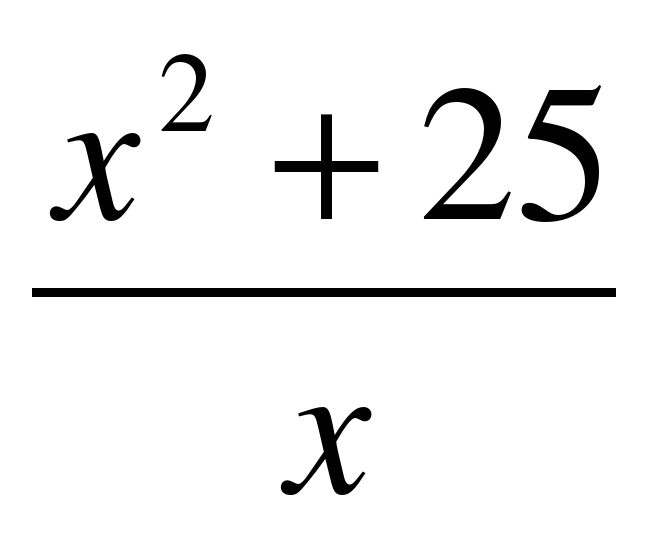 на отрезке [-12;-1].
на отрезке [-12;-1].
3. Найти число целых решений системы 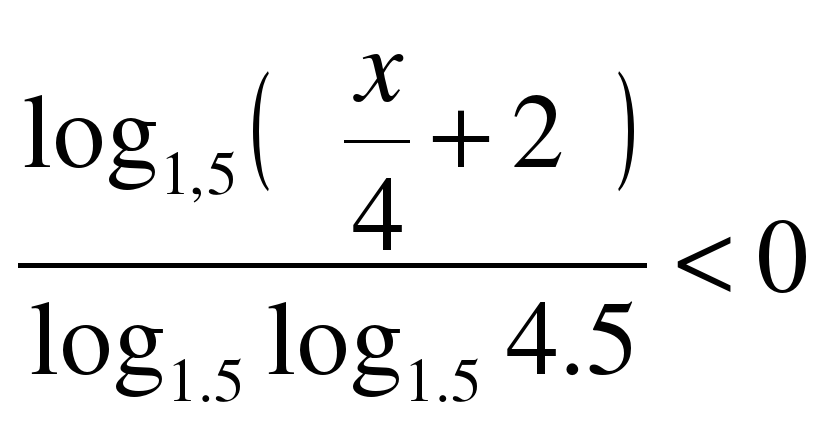 .
.
4. Найти число корней уравнения 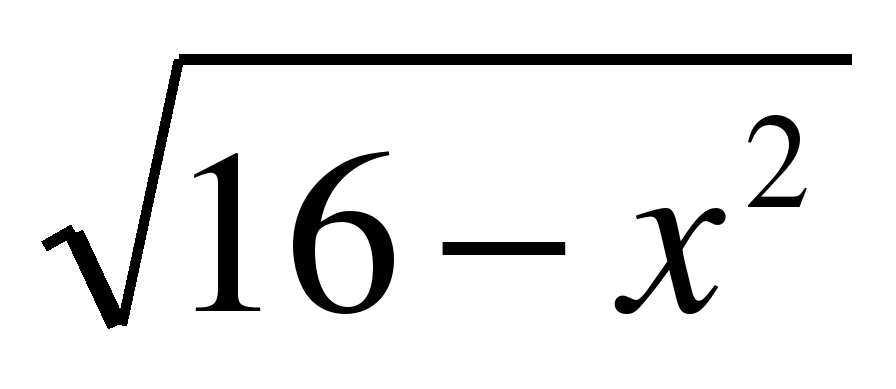 · sinx = 0.
· sinx = 0.
5. Укажите число корней уравнения tg2x · sin4x + cos4x – cos8x = 0 на промежутке [0;2П].
6. Найти все значения параметра а, при которых уравнение аx +  = 2а + 3 имеет единственный корень.
= 2а + 3 имеет единственный корень.
Вариант 2.
1. Вычислите: 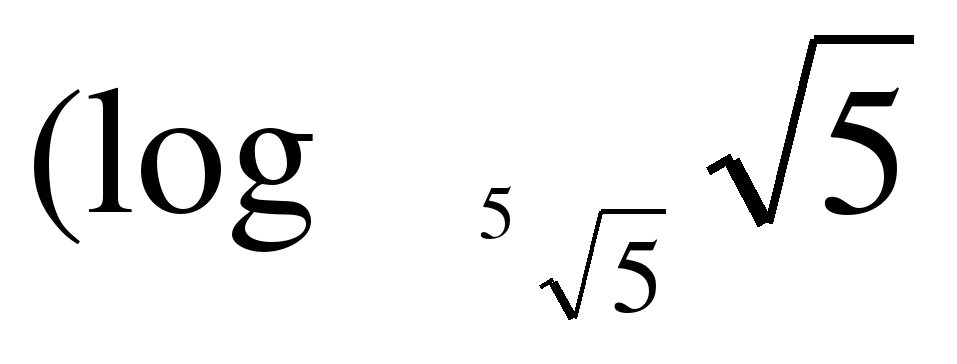 +
+ 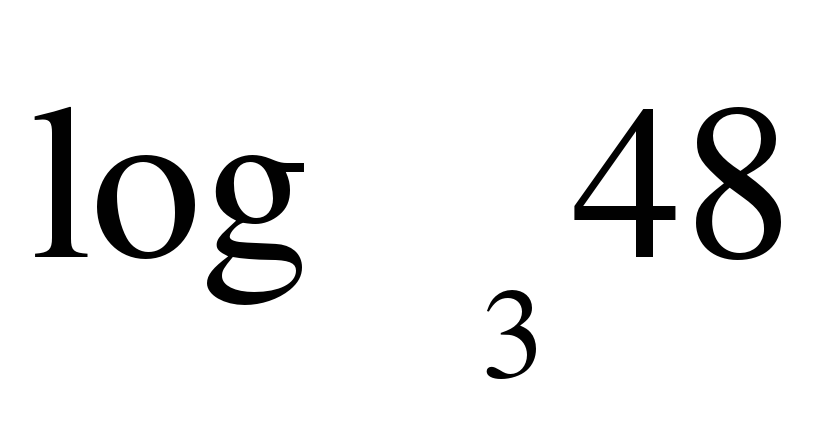 -
- 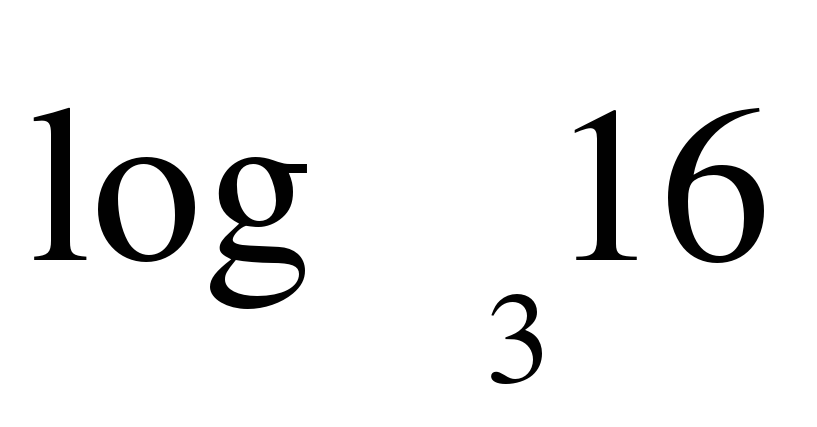 ) · 15
) · 15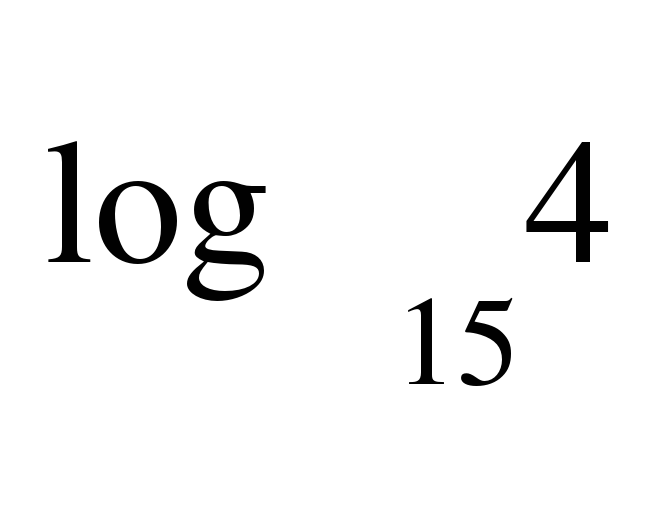 .
.
2. Найти наименьшее значение функции y=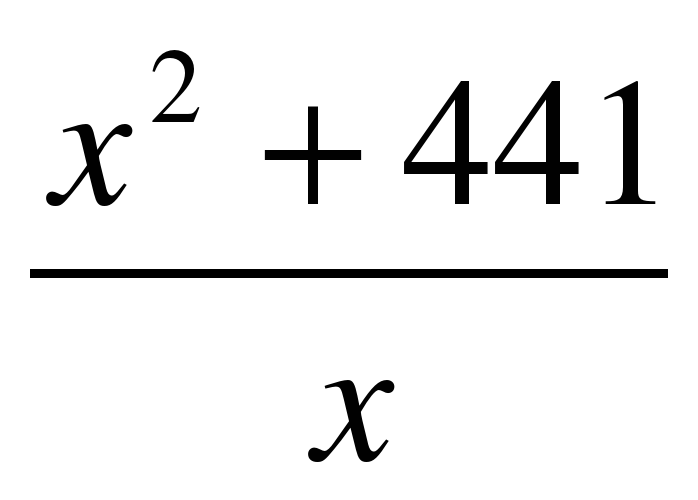 на отрезке [2;32].
на отрезке [2;32].
3. Найти число целых решений неравенства 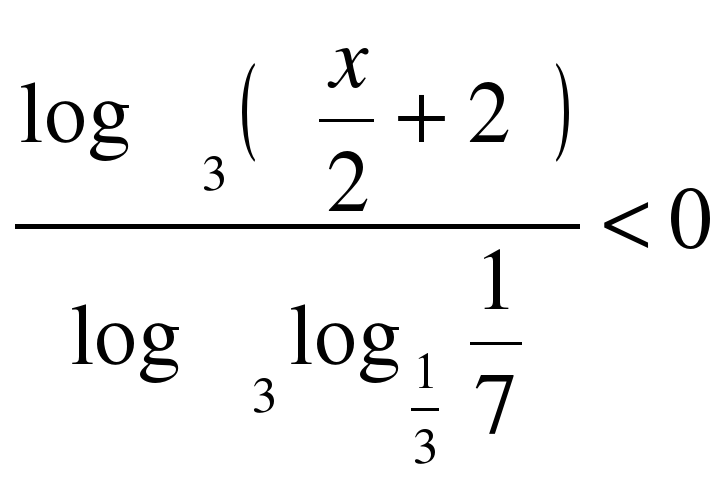 .
.
4. Найти число корней уравнения 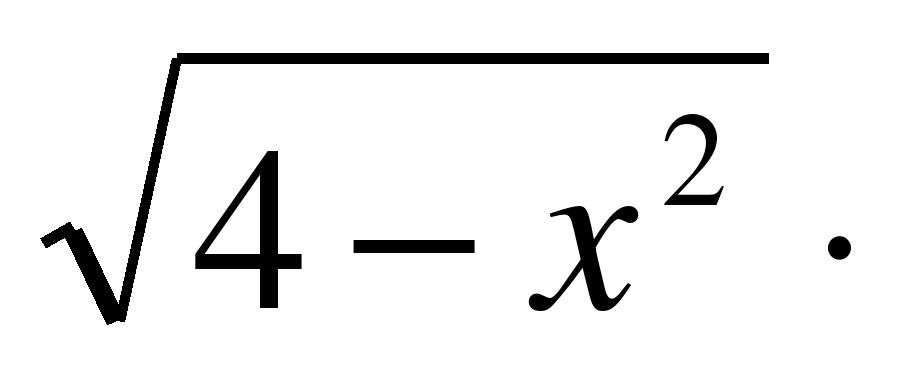 cosx = 0.
cosx = 0.
5. Укажите число корней уравнения tg4x · sin8x + cos8x – cos16x = 0 на промежутке [0;2П].
6. Найти все значения параметра а, при которых уравнение аx + 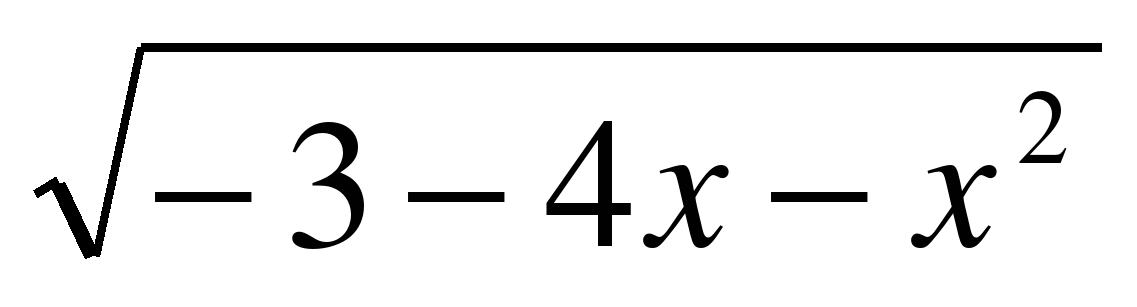 = 3а + 1 имеет единственный корень.
= 3а + 1 имеет единственный корень.
Тезисы.
Программа элективного курса составлена для учащихся 11 классов основной школы с целью систематизации знаний по ключевым темам алгебры и начал анализа и геометрии, что позволяет учащимся более качественно подготовиться к сдаче единого государственного экзамена по математике. Программа включает в себя разнообразие методов решения задач по основным темам курса алгебры и геометрии, в том числе задач, которые требуют применения традиционных знаний в измененной и нестандартной ситуациии.

 Получите свидетельство
Получите свидетельство Вход
Вход



 .
.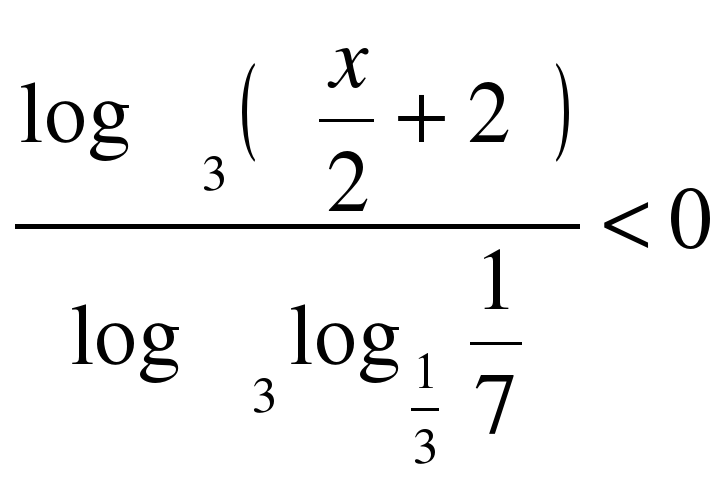 .
.








 Авторская программа элективного курса по математике «Решение задач повышенной сложности» (66 КB)
Авторская программа элективного курса по математике «Решение задач повышенной сложности» (66 КB)
 0
0 505
505 70
70 Нравится
0
Нравится
0



