Первый признак равенства треугольников.

Вспомним!

В

С

А

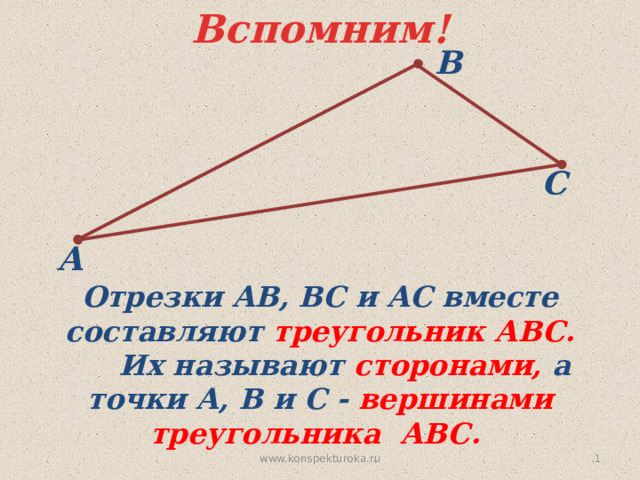
Отрезки АВ, ВС и АС вместе составляют треугольник АВС.

Их называют сторонами, а точки А, В и С - вершинами треугольника АВС.

www.konspekturoka.ru

7 класс геометрия

Урок № 11

Понятие треугольника и его элементы.

Равные треугольники

www.konspekturoka.ru

С

Вспомним!

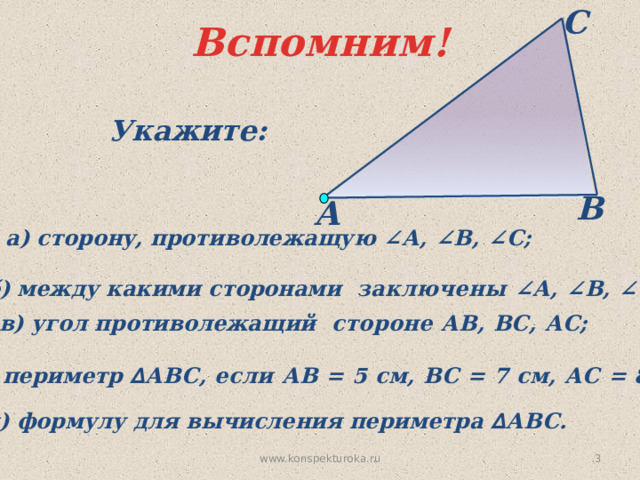
Укажите:

В

А

а) сторону, противолежащую ∠А, ∠В, ∠С;

б) между какими сторонами заключены ∠А, ∠В, ∠С;

в) угол противолежащий стороне АВ, ВС, АС;

г) периметр ∆ АВС, если АВ = 5 см, ВС = 7 см, АС = 8 см;

д) формулу для вычисления периметра ∆ АВС.

www.konspekturoka.ru

Вспомним!

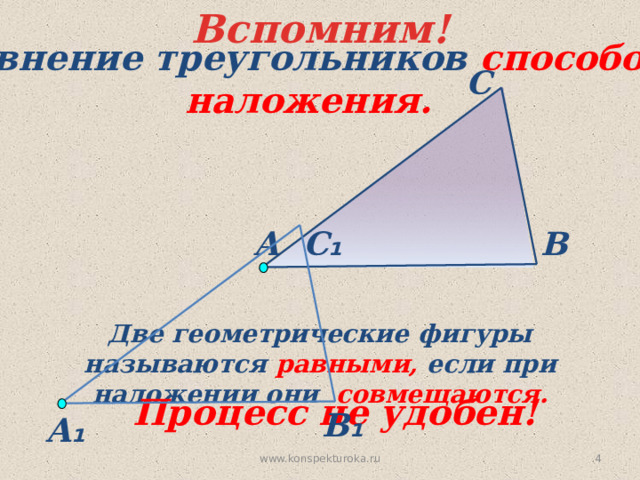
Сравнение треугольников способом

наложения.

С

С ₁

А

В

Две геометрические фигуры называются равными, если при наложении они совмещаются.

Процесс не удобен!

В ₁

А ₁

3

www.konspekturoka.ru

Вспомним!

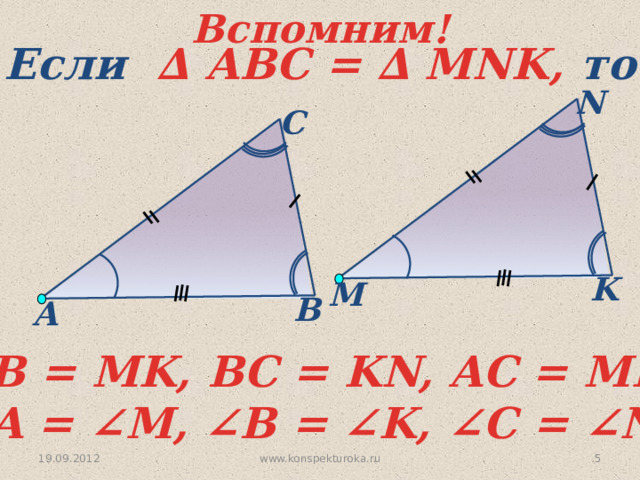
Если ∆ АВС = ∆ MNK, то

N

С

K

M

В

А

АВ = MK, BС = KN, AC = MN

∠ A = ∠M, ∠B = ∠K, ∠C = ∠N.

www.konspekturoka.ru

4

19.09.2012

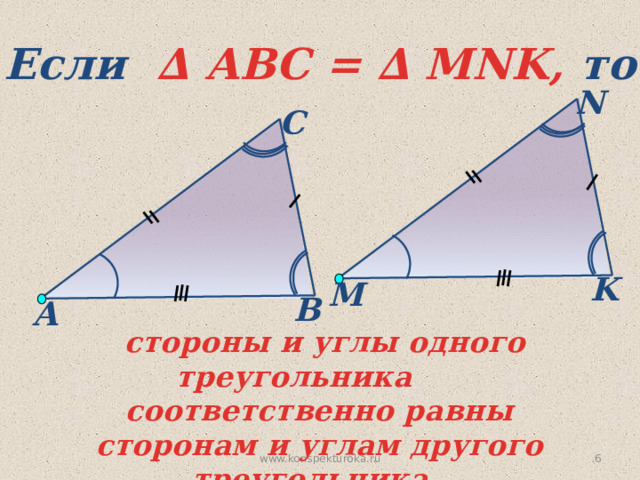
Если ∆ АВС = ∆ MNK, то

N

С

K

M

В

А

стороны и углы одного треугольника соответственно равны сторонам и углам другого треугольника.

5

www.konspekturoka.ru

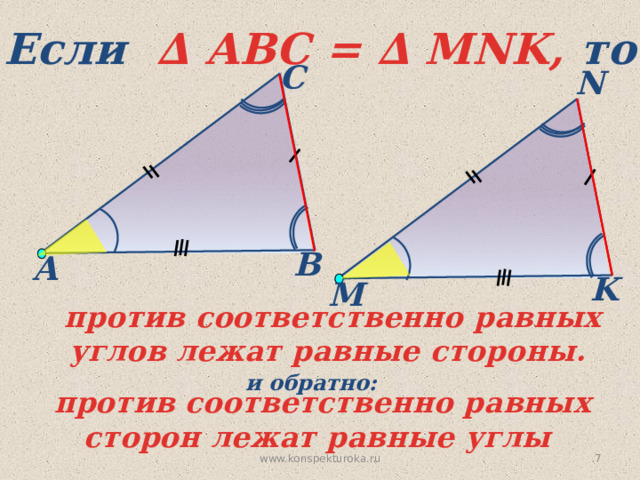
Если ∆ АВС = ∆ MNK, то

С

N

В

А

K

M

против соответственно равных углов лежат равные стороны.

и обратно:

против соответственно равных сторон лежат равные углы

6

www.konspekturoka.ru

С

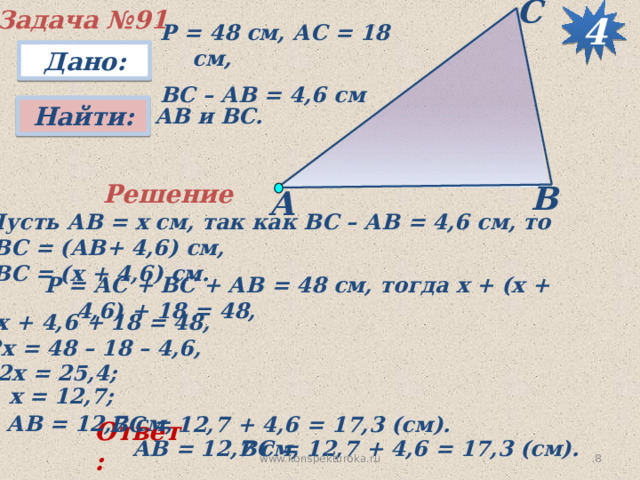
Задача №91

4

Р = 48 см, АС = 18 см,

ВС – АВ = 4,6 см

Дано:

Найти:

АВ и ВС.

В

Решение

А

Пусть АВ = х см, так как ВС – АВ = 4,6 см, то

ВС = (АВ+ 4,6) см,

ВС = (х + 4,6) см.

Р = АС + ВС + АВ = 48 см, тогда х + (х + 4,6) + 18 = 48,

2х + 4,6 + 18 = 48,

2х = 48 – 18 – 4,6,

2х = 25,4;

х = 12,7;

АВ = 12,7 см,

ВС = 12,7 + 4,6 = 17,3 (см).

Ответ:

ВС = 12,7 + 4,6 = 17,3 (см).

АВ = 12,7 см,

7

www.konspekturoka.ru

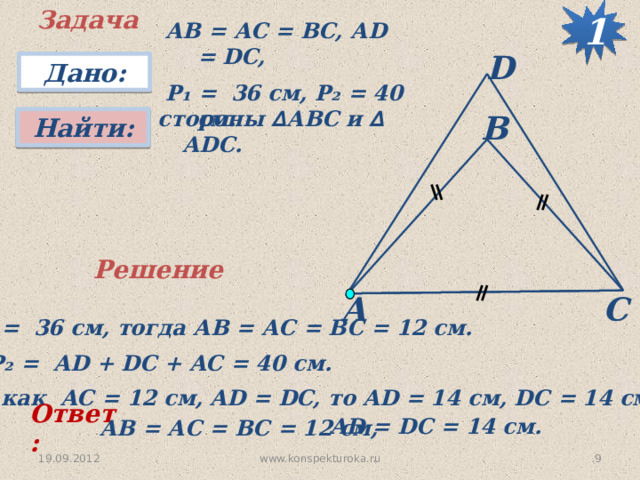
Задача

1

АВ = АС = ВС, АD = DC,

P ₁ = 36 см, P₂ = 40 см.

D

Дано:

стороны ∆ АВС и ∆ АDС.

В

Найти:

Решение

А

С

P ₁ = 36 см, тогда АВ = АС = ВС = 12 см.

P ₂ = AD + DC + AC = 40 см.

Так как AC = 12 см, AD = DC, то AD = 14 см, DC = 14 см.

Ответ:

AD = DC = 14 см.

АВ = АС = ВС = 12 см,

8

www.konspekturoka.ru

19.09.2012

2

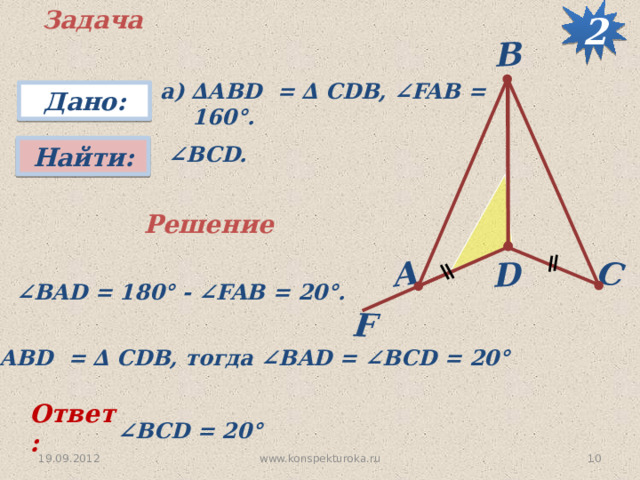
Задача

F

D

C

А

B

а) ∆АВD = ∆ CDB, ∠FAB = 160°.

Дано:

∠ BCD.

Найти:

Решение

∠ BAD = 180 ° - ∠FAB = 20 °.

∆ АВD = ∆ CDB, тогда ∠BAD = ∠BCD = 20 °

Ответ:

∠ BCD = 20 °

10

www.konspekturoka.ru

19.09.2012

3

F

D

C

А

B

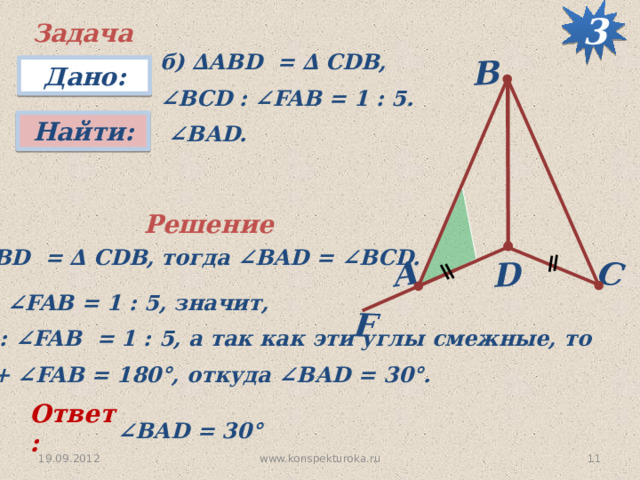
Задача

б) ∆АВD = ∆ CDB,

∠ BCD : ∠FAB = 1 : 5.

Дано:

Найти:

∠ BАD.

Решение

∆ АВD = ∆ CDB, тогда ∠BAD = ∠BCD.

∠ BCD : ∠FAB = 1 : 5, значит,

∠ BАD : ∠FAB = 1 : 5, а так как эти углы смежные, то

∠ BАD + ∠FAB = 180 °, откуда ∠BАD = 30 °.

Ответ:

∠ BАD = 30 °

19.09.2012

11

www.konspekturoka.ru

Ответить на вопросы:

• Какую фигуру называют треугольником?
• Что такое периметр треугольника?
• Какие треугольники называются равными?

Спасибо за внимание!

19.09.2012

www.konspekturoka.ru