Единицы измерения угловых величин

Цели и задачи: 

1) Дать понятие радианного измерения угловых величин, научить обучающихся переводить углы из градусной меры угла в радианную и обратно, отработать навык вычисления значений тригонометрических функций с помощью микрокалькулятора и отработать приобретённые знания при решение задач на нахождение неизвестных элементов прямоугольного треугольника;.

2) Развивать мыслительную деятельность, математическую речь, потребность к самообразованию, творческой деятельности студентов, умения решать задачи по заданному алгоритму

3) Воспитывать  познавательную активность через организацию совместных действий, ведущих к активизации учебного процесса; чувство ответственности через стимулирование студентов к самооценке образовательной деятельности; грамотность речи, аккуратность.

 Продолжительность занятия: 2часа

Материально-техническое обеспечение занятия: Проектор, компьютер, микрокалькуляторы, презентация к занятию, бейджики

Методическое и дидактическое обеспечение занятия: _Ведомость результатов, оценочный лист, карточки-задания для работы в группах, карточки для тестового контроля, опорные конспекты для повторения изученного, алгоритмы основных случаев решения прямоугольных треугольников, индивидуальные карточки с домашним заданием

Тип занятия: Комбинированный урок

Учитель сообщает тему занятия. Мы начинаем изучение нового раздела математики – Тригонометрии.

Задает вопросы:

В каких единицах измеряются углы?

Какие для этого есть приспособления?

В каком разделе математики вы изучали тригонометрию в школе?

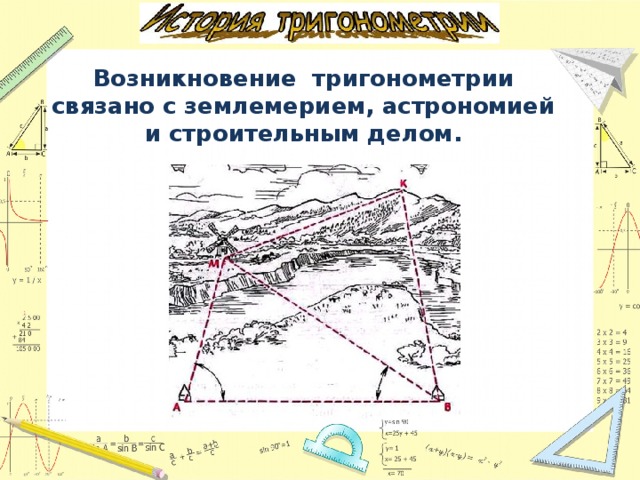
С чем было связано изучение тригонометрии в школе?

Как вы находили значение тригонометрических функций в школе?

Существуют ли другие единицы измерения углов?

Существуют ли другие способы измерения углов?

Студенты отвечают на вопросы преподавателя:

Угловые величины измеряются в градусах

Углы измеряются с помощью транспортира

Тригонометрию изучали в разделе «Геометрия»

Тригонометрические функции острого угла прямоугольного треугольника изучали для решения задач на нахождение неизвестных элементов треугольника.

Значение тригонометрических функций находили по таблицам Брадиса

Формулируют цели занятия:

Узнать о других единицах измерения угловых величин,

Научиться с ними работать,

Научиться вычислять значения тригонометрических функций углов в различных единицах измерения на калькуляторе,

Повторить решение задач на нахождение неизвестных элементов прямоугольного треугольника

Эпиграф к занятию: «Стоит только показать, что какая-либо вещь невозможна, как найдется математик, который ее сделает»  У. У. Сойер.

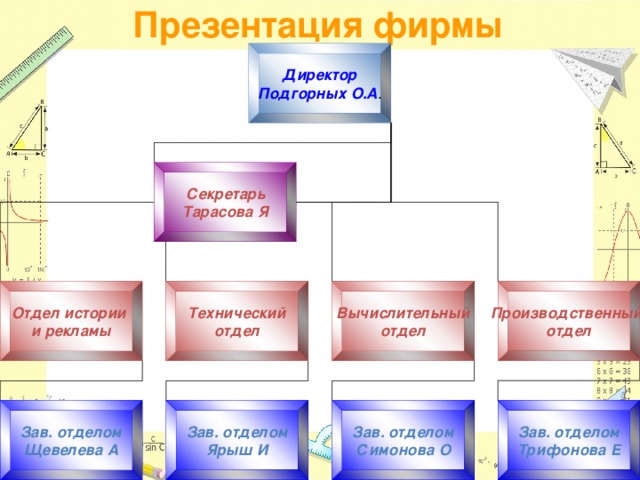
Каждый отдел представляет презентацию своей работы.

Объявляет презентацию первого отдела: «Отдела истории и рекламы»

Зав. Отделом рассказывает о работе отдела и представляет задачи, которые они решали.

План презентации:

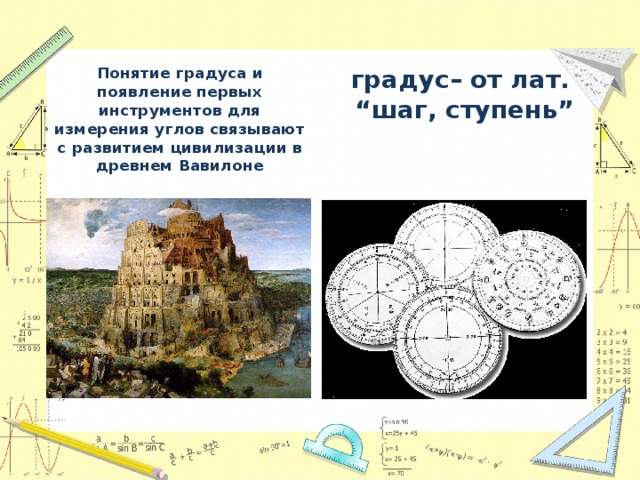
1. История измерений;

2. Единицы измерения угловых величин;

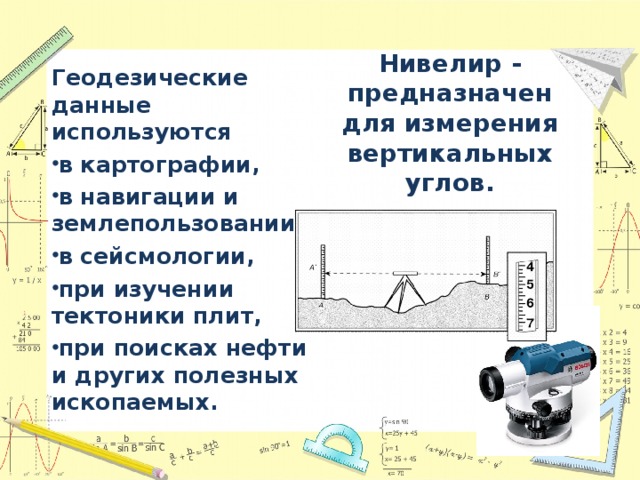
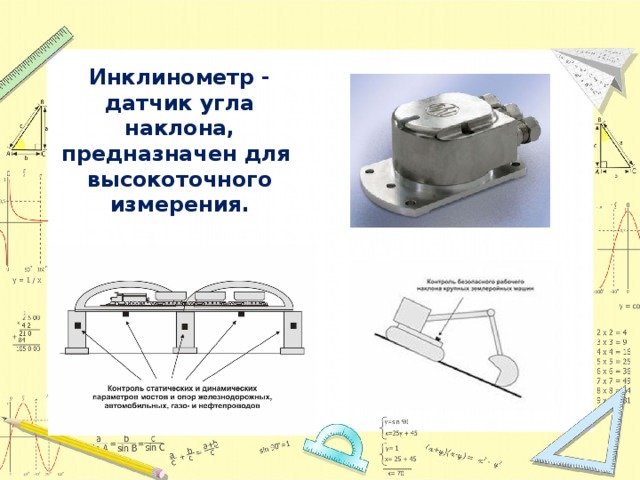
3. Современные приборы для измерения угловых величин (реклама);

4. История тригонометрии.

Чтобы дать оценку работы отдела, предлагается тестирование всех студентов. (у каждого на столе карточки 1, 2, 3. Выбирают на заданный вопрос номер ответа и поднимают его, зав. Отделом фиксирует правильные ответы в оценочном листе)

Секретарь собирает данные тестирования, выставляет оценки за первый этап урока и считает успеваемость и качество усвоения материала

Объявляет презентацию «Технического отдела»

Заведующий отделом рассказывает о работе своего отдела и предлагает план презентации:

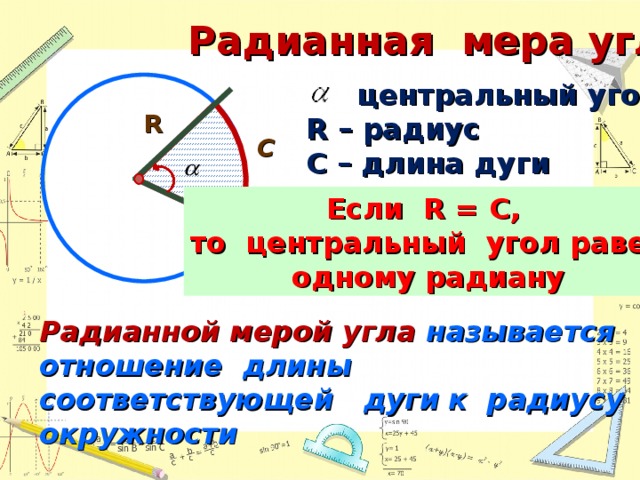
1. Понятие радиана;

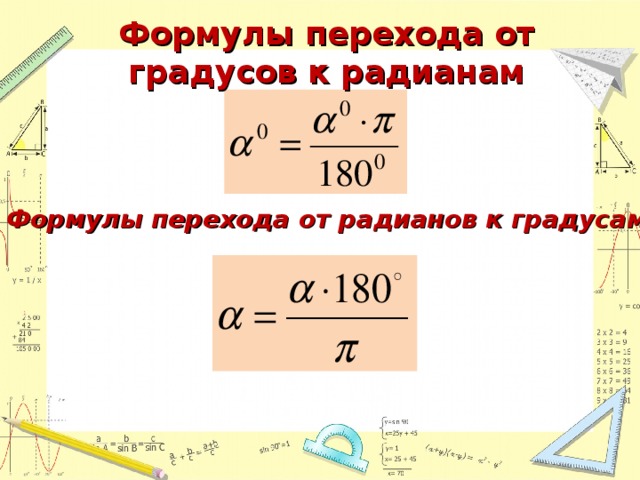
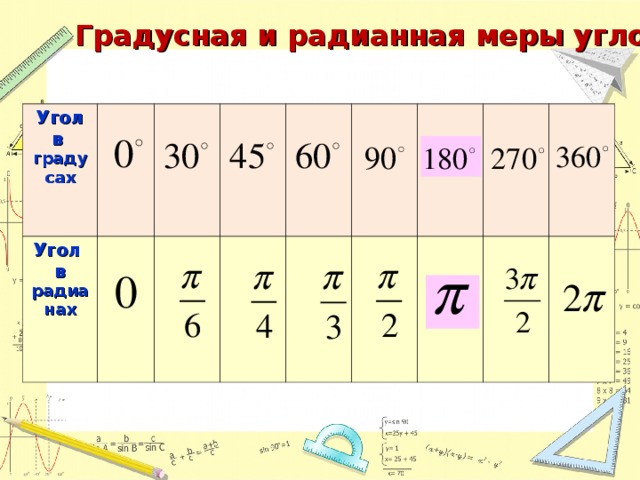
2. Формула перехода от градусов к радианам;

На закрепление работы предлагаю заполнить таблицу (у каждого на столе) По слайду осуществляют самопроверку и оценивают свой результат. Зав. отделом фиксируют результаты группы и передает секретарю.

Секретарь собирает данные тестирования, выставляет оценки за второй этап урока и считает успеваемость и качество усвоения материала.

Объявляет презентацию «Вычислительного отдела»

Заведующий отделом рассказывает о работе своего отдела и предлагает план презентации:

1. Микрокалькулятор и его возможности;

2. Вычисление значений тригонометрических функций углов в градусах на микрокалькуляторе;

3. Вычисление значений тригонометрических функций углов в радианах на микрокалькуляторе;

4. Вычисление углов по заданному значению тригонометрической функции

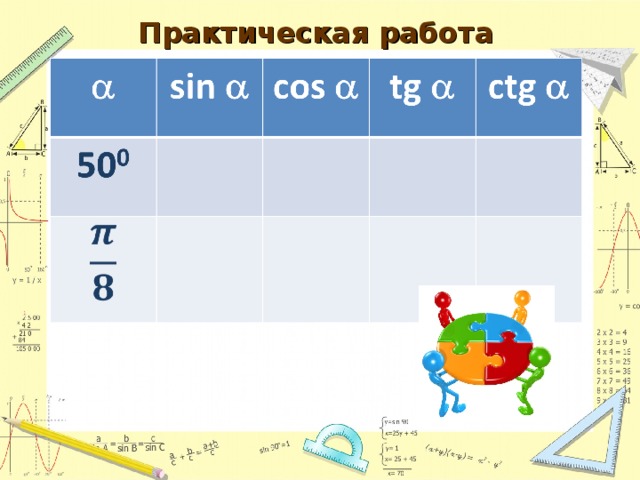
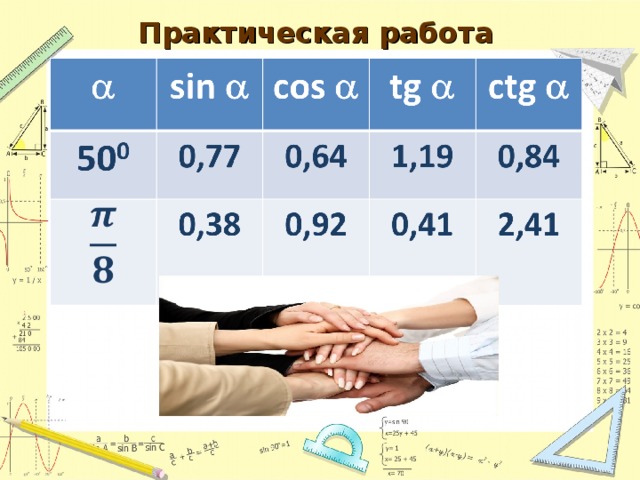
На закрепление предлагается работа в группах по вычислению значений тригонометрических функций с помощью калькулятора. (результаты заносятся в таблицу)  Проверка осуществляется по слайду с ответами и вся группа получает общую оценку.

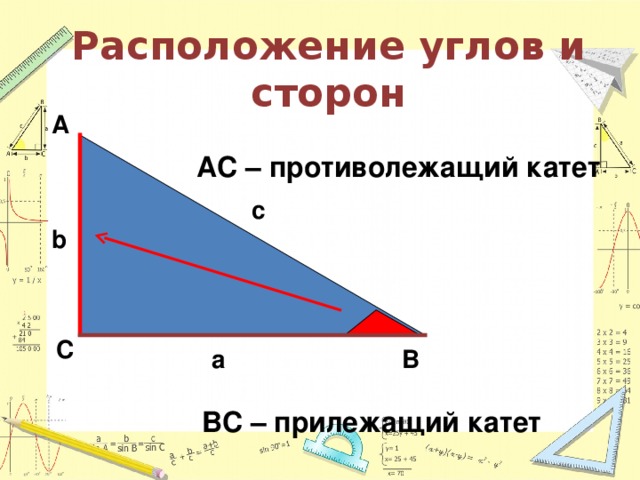
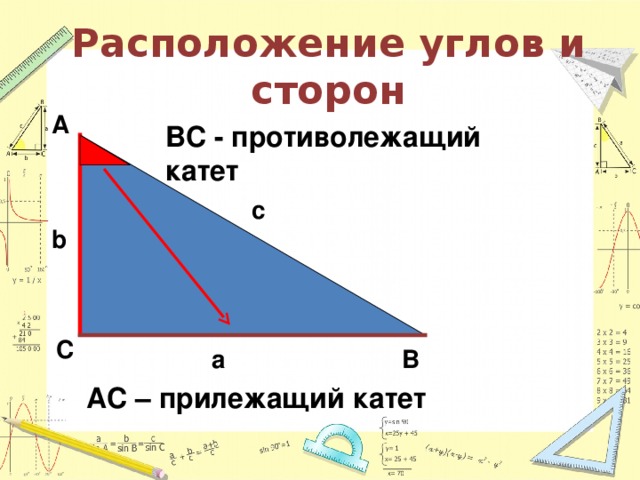
Тригонометрия – это наука о взаимосвязи углов и сторон треугольника. В основе множество задач геометрии используются задачи на решение прямоугольных треугольников

Под контролем преподавателя изображают прямоугольный треугольник и отрабатывают понятия: гипотенуза, катеты, противолежащий катет, прилежащий катет

Объявляет презентацию «Производственного отдела

Заведующий отделом рассказывает о работе своего отдела и предлагает план презентации:

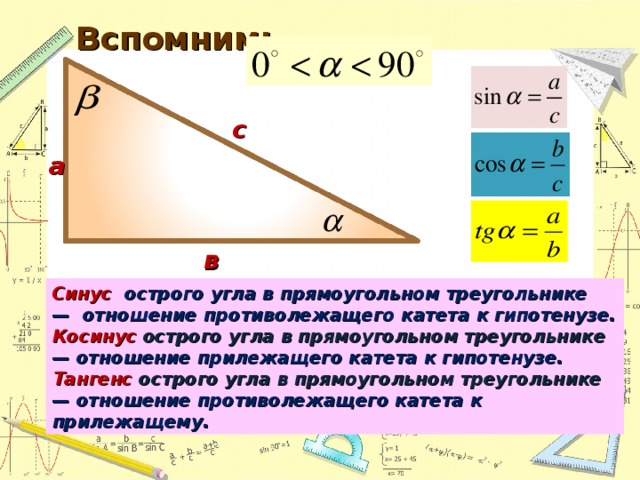
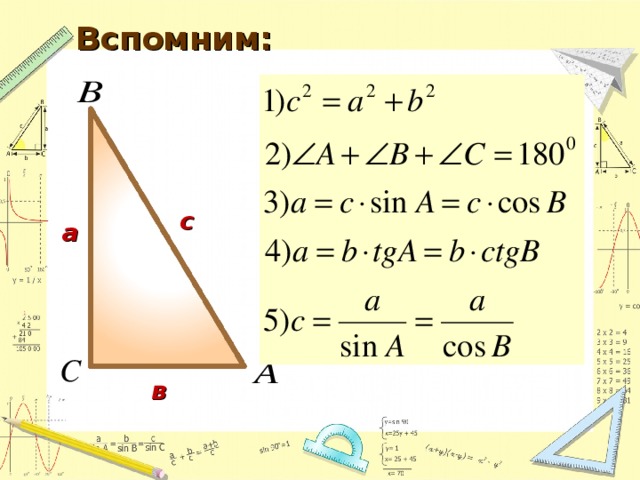
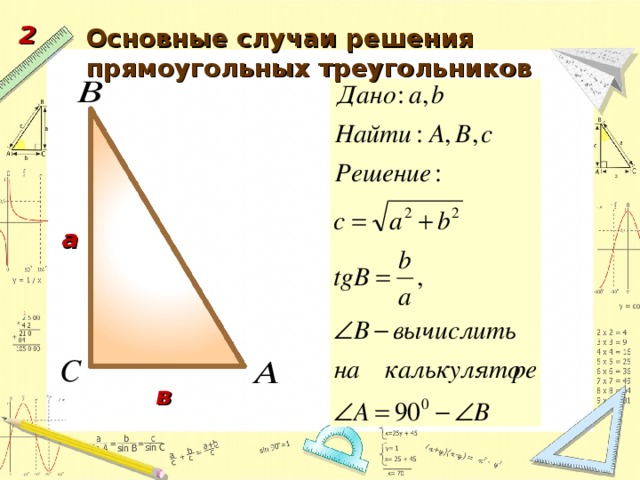
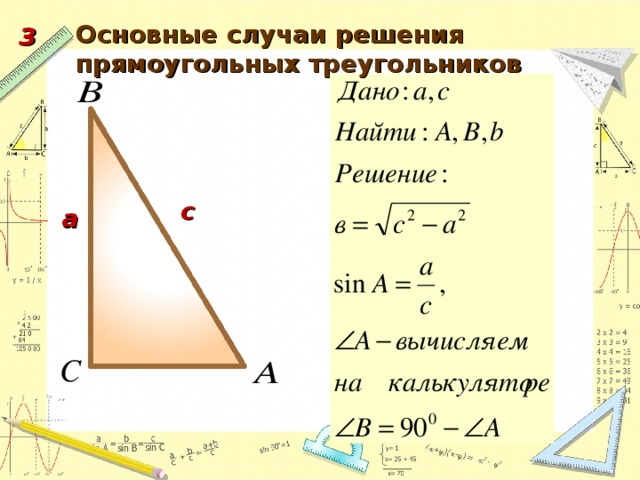
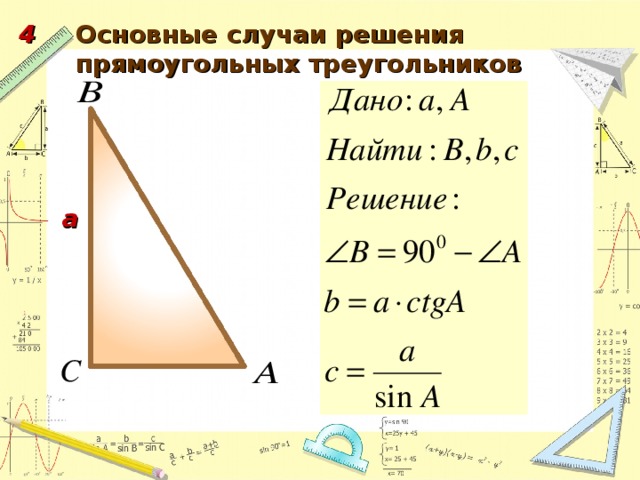
1. Повторить основные понятия тригонометрических функций острого угла прямоугольного треугольника, основные теоремы, известные из курса основной школы.

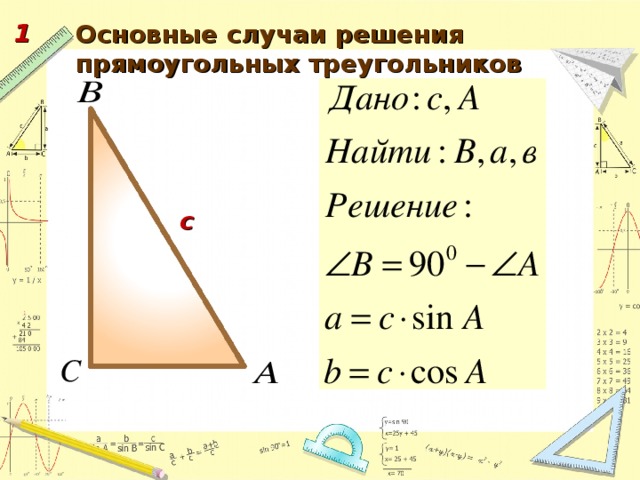
2. Систематизировать задачи по решению прямоугольных треугольников и решить задачи по каждому случаю.

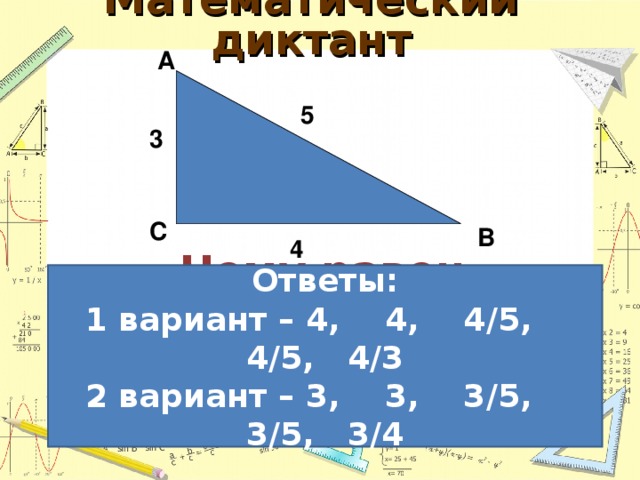
Для подведения итогов презентации предлагает математический диктант на 2 варианта

Обмениваются работами и проводят взаимопроверку по эталону ответов, предложенных на слайде. Выставляют друг другу оценку по критериям, предложенным преподавателем.

Зав. Отделами дают оценку своей работы и работы каждого члена команды. Студенты анализируют свою работу, реализацию целей, поставленных в начале занятия. Акцентируют внимание на своих ошибках и путях их исправления.

Домашнее задание: Выдаются индивидуальные карточки-задания с домашней работой. Типовой расчет на решение прямоугольных треугольников.

Секретарь дает оценку студентам на занятии, отмечает активных и неактивных студентов. Оценивает презентацию каждого отдела по проценту усвоения материала и качества усвоения.

Подводит итог занятия. Объявляет оценки.

Единицы измерения угловых величин

Стоит только показать, что какая-либо вещь невозможна, как найдется математик, который ее сделает.

У. У. Сойер

Презентация фирмы

Директор Подгорных О.А .

Секретарь Тарасова Я

Отдел истории и рекламы

Технический отдел

Вычислительный отдел

Производственный отдел

Зав. отделом Щевелева А

Зав. отделом Ярыш И

Зав. отделом Симонова О

Зав. отделом Трифонова Е

ПРЕЗЕНТАЦИЯ ОТДЕЛА ИСТОРИИ И РЕКЛАМЫ

Заведующий отделом: Щевелева Анастасия

Историческая справка

Транспортир –

происходит от французского слова, что означает “переносить”.

Диоптр – прибор позволяющий измерять углы на местности и решать множество прикладных задач.

Герон Александрийский ( I в. до н.э)

Астролябия - угломерный прибор, служивший до начала XVIII в. для определения положений светил на небе .

В 1731 году английский оптик Джон Хэдли усовершенствовал астролябию

Октант – прибор, позволяющий решить проблему измерения широты на движущемся судне

Секстант это наиболее совершенный прибор для измерения угловых координат небесных тел того времени. Его изобретение приписывается Исааку Ньютону. Секстант позволял измерять как широту, так и долготу точки наблюдения, причем с довольно высокой точностью.

Теодолит – инструмент, который совместил в себе сразу два прибора – горизонтальный и вертикальный угломер и зрительную трубу. Он стал первым геодезическим инструментом измерения углов с градуированным полем зрения.

Понятие градуса и появление первых инструментов для измерения углов связывают с развитием цивилизации в древнем Вавилоне

градус– от лат. “шаг, ступень”

Артиллеристы придумали совсем иную меру углов. Мера эта - "тысячная", или, как ее называют иначе, "деление угломера". Чтобы получить тысячную, окружность делят на 6000 частей.

В морской навигации в качестве основной единицы измерения принято использовать румб. Морской румб определяется центральным углом, соответствующим дуге, равной 1/32 части окружности.

Радиан

За единицу принимается острый угол под которым видна из центра окружности дуга, равная радиусу окружности.

Центезимальная система: наиболее часто эта система измерения углов употребляется в ГЕОДЕЗИЧЕСКИХ измерениях.

За единицу принимается 1/100 часть прямого угла. Единица измерения называется ГРАДОМ.

1g = 0,01570796 радиан, 1g = 0,900° или 1° = 1,111g.

Часовая система: угол, полученный поворотом луча на 1/24 часть одного полного оборота.

Единица измерения называется ЧАСОМ.

Научно-технический прогресс наложил отпечаток и на совершенствование измерительной техники самого высокого уровня, однако принципы их работы и назначение изменились мало за прошедшие десятилетия и даже столетия.

Нивелир - предназначен для измерения вертикальных углов.

Геодезические данные используются

• в картографии,
• в навигации и землепользовании,
• в сейсмологии,
• при изучении тектоники плит,
• при поисках нефти и других полезных ископаемых.

Теодолит. Его функционал дополнен возможностью измерения и горизонтальных, и вертикальных углов.

Дальномер

Идеальный инструмент для любой стройплощадки

Тахеометр

С помощью современных тахеометров можно измерять расстояние до объектов, что значительно упрощает съемки и расчеты, они оборудованы системой GPS и встроенным компьютером для обработки и хранения данных

Авиагоризонт - гироскопический прибор для измерения углов крена и тоннажа летательного аппарата.

Автоколлиматор – прибор, предназначенный:

- для точных угловых измерений;

- для установки параллельности и перпендикулярности поверхностей.

Гониометр - прибор для измерения углов между плоскими полированными гранями твердых прозрачных и непрозрачных тел.

Сейчас в практике лесохозяйственных работ вообще, а также непосредственно при отмежевании участков главного пользования или рубок ухода, достаточно широко используются гониометры.

Делительная оптическая головка - прибор, предназначенный:

- для измерения центральных углов деталей;

- для выполнения разметочных и делительных работ.

Дифферентометр - прибор для измерения в метрах или градусах дифферента судна.

Измерительный проектор - прибор, предназначенный для измерения и контроля линейных и угловых размеров изделий, принцип действия которого основан на нормированном увеличении изображений этих изделий на экране, что позволяет проводить измерения с помощью

- специального устройства на измерительном столе;

- чертежа, накладываемого на экран.

Инклинометр - датчик угла наклона, предназначен для высокоточного измерения.

Кренометр - прибор для измерения угла крена судна. Кренометр устанавливается в ходовой рубке.

Пеленгатор - устройство для определения углового направления (пеленга) на объект.

Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников.

Возникновение тригонометрии связано с землемерием, астрономией и строительным делом.

Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2в. до н.э.) и Клавдием Птолемеем (2в.н.э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.

Гиппарх

Птолемей

В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли.

Отрезок АВ он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов оно было заменено латинским синус (sinus – изгиб, кривизна).

Слово косинус намного моложе. Косинус – это сокращение латинского выражения, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”; cosa = sin( 90° - a)).

Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов.

в XIV веке благодаря трудам немецкого математика, астронома Регимонтана (1467г.); плоская и сферическая тригонометрия стала самостоятельной дисциплиной в Европе.

Название «тангенс», происходящее от латинского (касаться), появилось в 1583 г. и переводится как «касающийся» (линия тангенсов – касательная к единичной окружности).

Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иоганна Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

Николай Коперник

Тихо Браге

Иоганн Кеплер

Франсуа Виет

Астрономов интересовали соотношения между сторонами и углами сферических треугольников. И надо заметить, что математики древности удачно справлялись с поставленными задачами.

Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т.д.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком в XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук.

Тест по истории измерений

1. Первый прибор, который позволял измерять углы на местности и решать множество прикладных задач:

1) Астролябия

2) Диоптр

3) Секстант

2. Создатель астролябии, с помощью которой стало возможным определение времени и продолжительности дня и ночи, астрологических предсказаний, осуществление некоторых математических вычислений.

1) Евдокс

2) Ньютон

3) Хэдли

3. Какая система счисления позволила в Вавилоне делить окружность на 360 частей, называемую мерой измерения угла в градусах?

1) Десятеричная

2) Шестидесятеричная

3) Двенадцатеричная

4. За какую единицу принимается острый угол под которым видна из центра окружности дуга, равная радиусу окружности.

1) Градус

2) Град

3) Радиан

5. Благодаря какому ученому тригонометрия приобрела современный вид: аналитической теории тригонометрических функций?

1) Кеплер

2) Виет

3) Эйлер

ПРЕЗЕНТАЦИЯ ТЕХНИЧЕСКОГО ОТДЕЛА

Заведующий отделом: Ярыш Ирина

Радианная мера угла

центральный угол

R – радиус

С – длина дуги

R

С

Если R = C ,

то центральный угол равен

одному радиану

Радианной мерой угла называется отношение длины соответствующей дуги к радиусу окружности

Формулы перехода от градусов к радианам

Формулы перехода от радианов к градусам

Градусная и радианная меры углов

Угол

в градусах

Угол

в

радианах

ПРЕЗЕНТАЦИЯ ВЫЧИСЛИТЕЛЬНОГО ОТДЕЛА

Заведующий отделом: Симонова Олеся

Вычисления на микрокалькуляторе

1 регистр

2 регистр

2ndF

sin

Переход на 2 регистр

Вычисление sin угла

sin -1

cos

Вычисление cos угла

Вычисление угла по sin

tan

cos -1

Вычисление tg угла

Вычисление угла по cos

Переход от градусной меры угла к радианной

DRG

tan -1

Вычисление угла по tg

1/x

Вычисление обратной функции

П

Число П

Практическая работа

Практическая работа

Расположение углов и сторон

А

АС – противолежащий катет

c

b

С

В

a

ВС – прилежащий катет

Расположение углов и сторон

А

ВС - противолежащий катет

c

b

С

В

a

АС – прилежащий катет

ПРЕЗЕНТАЦИЯ ПРОИЗВОДСТВЕННОГО ОТДЕЛА

Заведующий отделом: Трифонова Евгения

Вспомним:

с

а

в

Синус острого угла в прямоугольном треугольнике — отношение противолежащего катета к гипотенузе.

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе.

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему.

Вспомним:

с

а

в

58

1

Основные случаи решения прямоугольных треугольников

с

59

2

Основные случаи решения прямоугольных треугольников

а

в

60

Основные случаи решения прямоугольных треугольников

3

с

а

61

4

Основные случаи решения прямоугольных треугольников

а

62

Математический диктант

А

5

3

С

В

4

Найдите tg угла (1в) A (2в) B

Чему равен прилежащий катет для угла (1в) В (2в) А

Найдите cos угла (1в) B (2в) A

Найдите sin угла (1в) А (2в) В

Ответы:

1 вариант – 4, 4, 4 /5, 4/5, 4/3

2 вариант – 3, 3, 3 /5, 3/5, 3/4

Чему равен противолежащий катет для угла (1в) А (2в) В

63