Логарифмы и их свойства

Тема урока: «Логарифмы и их свойства».

Разработала: преподаватель математики Сарычева С.В.

Цель урока:

- дать представление о логарифмах и свойствах логарифма, рассмотреть решение примеров на применение свойств логарифмов;

- развивать логическое мышление, внимание, познавательный интерес коммуникативных навыков;

- формировать интерес к предмету, развивать математическую речь обучающихся.

Тип урока: изучение нового материала.

Форма работы: фронтальная, индивидуальная.

Оборудование:

Ход урока.

1. Организационный момент. (5 минуты)

Проверить готовность группы и кабинета к учебному занятию и отметить отсутствующих на уроке.

На предыдущем уроке мы закончили изучение темы, связанной с решением показательных уравнений и неравенств и сегодня переходим к изучению новой важной темы. Но в начале давайте дадим толчок нашим мыслительным процессам и для этого я предлагаю вам разгадать два ребуса:

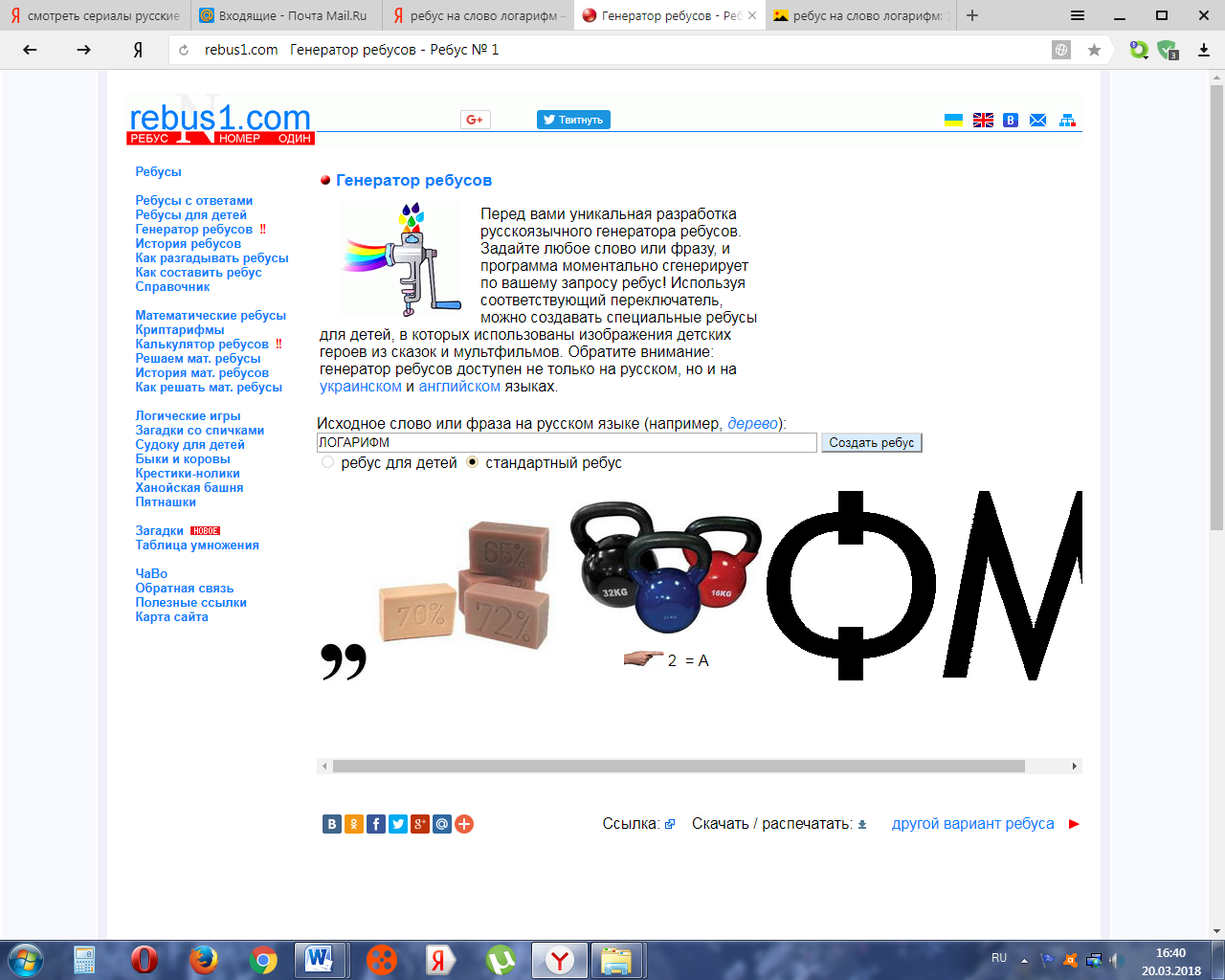(Логарифм)

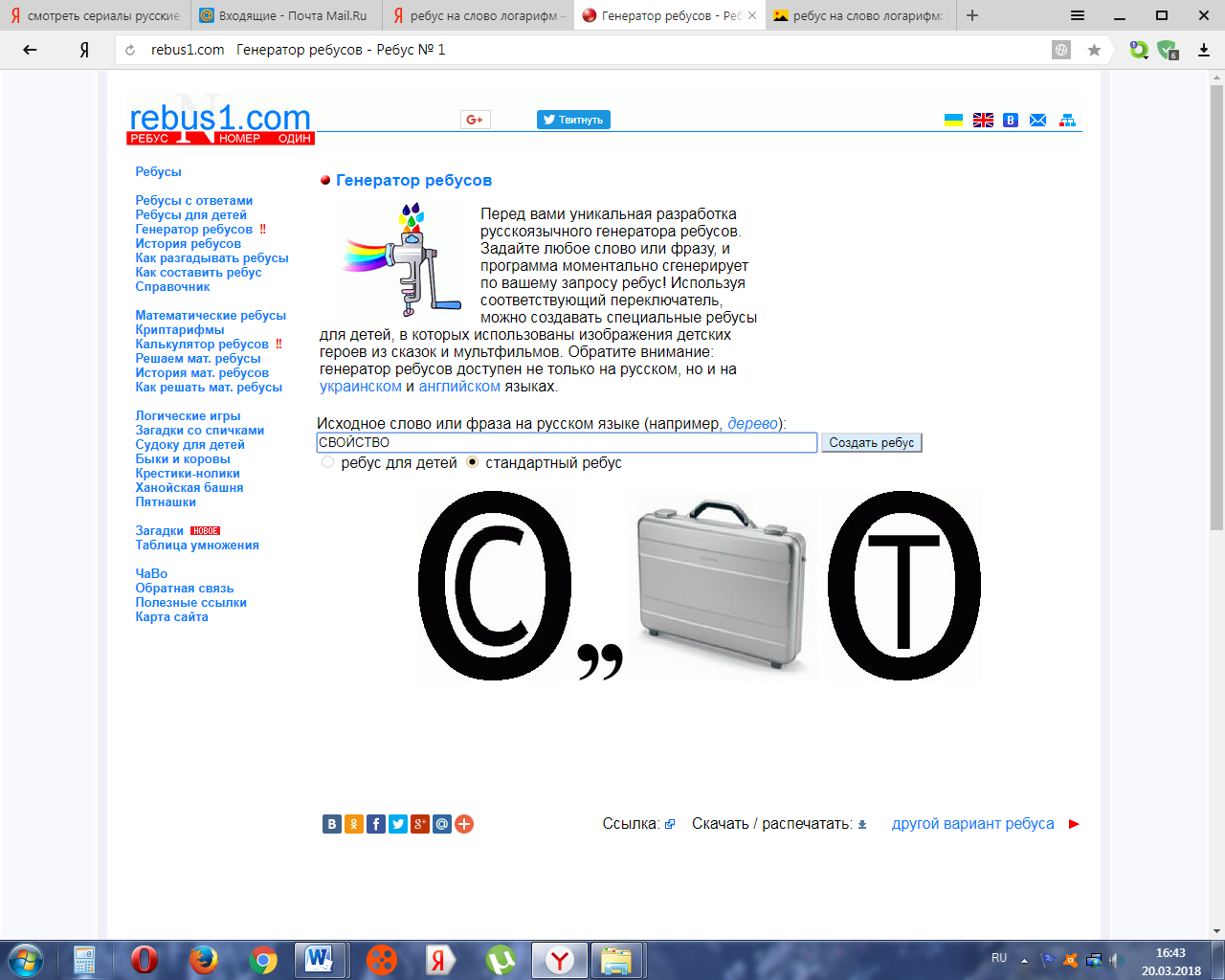(Свойство)

1. Объяснение нового материала. (15 минут)

Итак, записываем тему урока: «Логарифмы и их свойства».

Изучение логарифмов и логарифмической функции вам потребуется в первую очередь для сдачи экзамена по математике, а также эти знания имеют прикладное значение в областях естествознания, таких как: физика, химия, биология, география, астрономия, а также в экономике банковского дела и производствах. И вы в этом убедитесь, если после окончания техникума решите получать высшее образование.

Термин логарифм был предложен шотландским математиком любителем Джоном Непером в 1614 году. Принцип, лежащий в основе любой системы логарифмов, известен очень давно и может быть прослежен вглубь истории вплоть до древневавилонской математики (около 2000 до н.э.). Близкое к современному понимание логарифмирования - как операции, обратной возведению в степень -впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. Но первую логарифмическую линейку, которую еще ваши дедушки и бабушки применяли в школе для вычисления логарифмов изобрели уже 1620 годы Эдмунд Уингейт и Уильям Отред. До появления карманных калькуляторов это был незаменимый инструмент инженера.

А сейчас, давайте вернемся от истории к теме нашего урока и рассмотрим решение двух показательных уравнений: 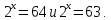Первое уравнение решается легко, так 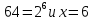и это единственный корень уравнения. Второе уравнение также имеет единственное решение, но оно в отличии от первого будет являться иррациональным числом. (Кто помнит какие числа называются иррациональными?) Вот для обозначения такого корня ввели новое понятие и обозначение - логарифм, то есть .

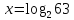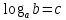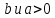Итак, , где и 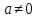, такое что .

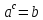a – основание логарифма, b – логарифмируемое выражение. Вычислить логарифм – это значит найти показатель степени. В которую надо возвести основание. Чтобы получить логарифмируемое выражение.

Примеры.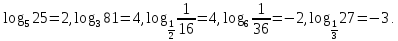

Назовите в приведенных примерах основание логарифма и логарифмируемое выражение.

Познакомимся с основным логарифмическим тождеством и со свойствами логарифмов.

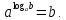
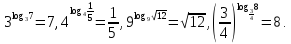
Вычислите: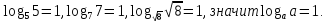

Вычислите: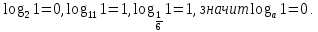

Вычислите: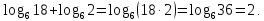

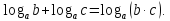
Вычислите: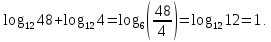

.

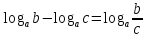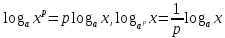
Вычислите: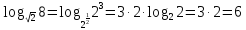

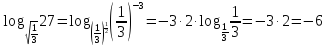
1. Закрепление изученного материала. (15 минут)

Работа по учебнику, устно № 479, № 488.

Работа у доски № 489(а, б), № 490(а, б), № 495(а, б), №497(а).

1. Проверка изученного материала. (5 минут)

На слайде презентации даны задания по вариантам. Время выполнения 3 минуты. После решения идет обмен тетрадями и взаимопроверка с выставлением оценок. Правильные ответы представлены на слайде.

Задания 1 варианта.

Вычислите: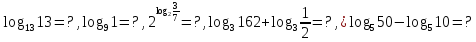

Задания 2 варианта.

Вычислите: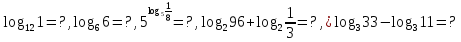

Правильные ответы.

1 вариант: 1,0,3/7,4,1.

2 вариант: 0,1,1/8,5,1.

1. Разбор домашнего задания. (3 минуты)

№489, №490, №495(в, г), №497(г).

1. Рефлексия. (2 минуты)

Ответьте, пожалуйста, на вопросы:

- что мы изучали на уроке?

- что значит вычислить логарифм?

- в каком веке впервые появилось понятие логарифма?

Посмотрите на слайд и поднимите сначала руки те, кто доволен своей работой на уроке, потом те, кто считает, что работал на уроке неплохо, и теперь те, кому на уроке было трудно.

Тема урока:

«Логарифмы

и их свойства».

1614 год

Джон Валлис,

1616 -1703 гг.

английский математик

Иоганн Бернулли,

1667 -1748 гг.

швейцарский математик

Леонард Эйлер,

1707 -1783 гг.

швейцарский математик

1620 год

Эдмунд Уингейт и Уильям Отред

Проверочная работа

1 вариант

2 вариант

Правильные ответы

2 вариант

1 вариант