Простейшие задачи в координатах

Вам уже знакомо понятие вектора. Вы знаете, что называют его длиной. Также вам известен частный случай расположения векторов относительно друг друга. А именно коллинеарные векторы, среди которых выделяют сонаправленные и противоположно направленные.

Равными называют сонаправленные векторы, длины которых равны. А вот противоположно направленные векторы, длины которых равны, называют противоположными.

Так же вы уже знакомы с правилами построения вектора суммы двух и нескольких векторов, к ним относят правило треугольника, параллелограмма и многоугольника.

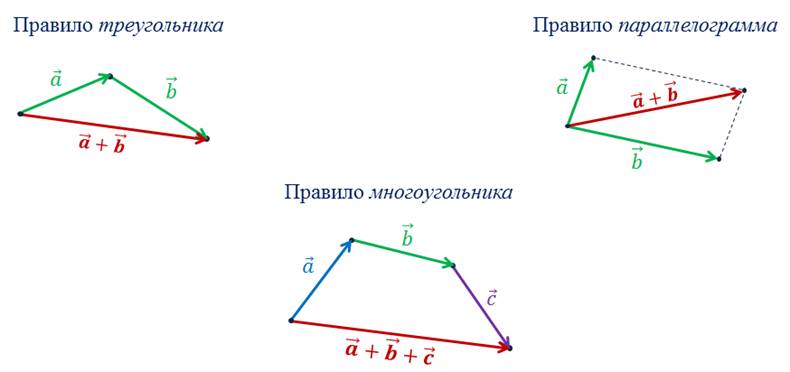
Ещё, вы уже умеете строить вектор разности двух векторов и вектор произведения вектора на число.

Также вам знакомо правило выражения вектора через коллинеарный ему и правило разложения вектора по двум неколлинеарным векторам.

- единичные векторы

, координаты вектора,

Последнее, которое помогло нам ввести понятие координат вектора. После чего мы сформулировали правила нахождения координат вектора суммы, разности и произведения вектора на число, которые позволяют определять координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.

И, наконец, введя понятие радиус-вектора, мы доказали, что координаты точки равны соответствующим координатам её радиус-вектора. Это утверждение позволило выразить координаты произвольного вектора как разность соответствующих координат его конца и начала.

Все ваши знания о векторах позволят применять методы алгебры при изучении геометрических фигур и их свойств. Похожие приёмы мы использовали при определении координат вершины параллелограмма по известным координатам трёх оставшихся вершин.

Такой подход к изучению свойств геометрических фигур называется методом координат.

И на этом уроке мы рассмотрим три вспомогательных задачи, которые и будем использовать при решении геометрических задач методом координат.

Первой решим задачу на определение координат середины отрезка.

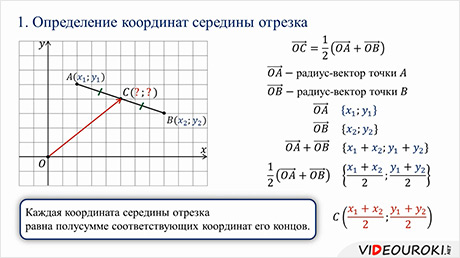
1.     Определение координат середины отрезка

Пусть точка   и точка — некоторые точки координатной плоскости. Точка С — середина отрезка AB. И нам необходимо определить её координаты.

Воспользуемся ранее доказанным утверждением и на основании того, что C — середина AB, запишем, что вектор   равен полусумме векторов   и .

Векторы   и  являются радиус-векторами точек А и B соответственно. Значит, координаты вектора , а координаты вектора .

Вектор их суммы будет иметь координаты .

Координаты вектора их полусуммы равны  .

Эти значения и будут координатами вектора , который в свою очередь является радиус-вектором точки C.

А это значит, что координаты точки C равны соответствующим координатам её радиус-вектора .

Таким образом, мы получили, что каждая координата середины отрезка равна полусумме соответствующих координат его концов.

Найти координаты точки , являющейся серединой отрезка .

Решение.

Задача. Даны точки  и . Найти координаты точек  и , если  — середина , а  —середина .

Решение.

 =

 2. Вычисление длины вектора по его координатам

От начала координат отложим вектор  равный вектору . Проведём перпендикуляры АА₁ и АА₂ к осям.

Если точка А имеет координаты , то и её радиус-вектор  имеет соответственно такие же координаты. При этом координаты вектора  также равны икс и игрек, ведь векторы  и  равны.

Итак, можно сказать, что длина отрезка , а длина отрезка .

Длину отрезка ОА можем выразить из прямоугольного треугольника

,

Получаем, что длина вектора , причём от какой бы точки он не был отложен.

Вычислить длины векторов , ,  и . , , , .

А теперь решим задачу.

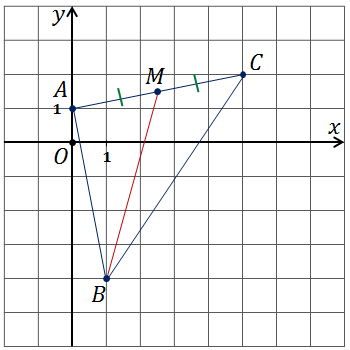
Задача. Найти длину медианы , треугольника , если , , .

Решение.

Ответ: .

Запишем ответ.

Далее решим последнюю вспомогательную задачу.

3. Определение расстояния между двумя точками

Пусть точка , а точка .

Выразим расстояние d между этими точками через их координаты.

Для начала рассмотрим вектор .

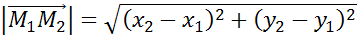
Тогда длина этого вектора равна корню квадратному из суммы квадратов его координат.

Но с другой стороны, длина , которая равна расстоянию d между данными точками.

Отсюда получаем, что расстояние между двумя точками находят как корень квадратный из суммы квадратов разностей соответствующих координат данных точек. Можно сказать также, что данная формула служит для нахождения длины отрезка по координатам его концов.

Найти расстояние между точками  и .

1. ,

2. ,

3. ,

Выполним задание.

Задача. На оси  и на оси  найти точки равноудалённые от точек  и .

Решение.

Ответ: , .

Подведём итоги нашего урока.

Сегодня мы познакомились с методом координат решения геометрических задач.

При этом рассмотрели три вспомогательные задачи: определение координат середины отрезка, вычисление длины вектора по его координатам и определение расстояния между точками.

Этими формулами мы будем пользоваться в дальнейшем при решении задач.