Перемещение при прямолинейном равномерном движении

Мы уже знаем, что для определения положение тела в любой момент времени, необходимо знать вектор перемещения, так как именно он связан с изменением координат движущегося тела. Проекции вектора перемещения тела на координатные оси просто равны изменениям его координат.

— Но как найти вектор перемещения? Что для этого нужно знать?

Ответ на этот вопрос зависит от того, какое движение совершает тело.

Рассмотрим сначала самый простой вид движения — равномерное прямолинейное движение (сокращённо РПД).

Из седьмого класса вы знаете, что движение, при котором за любые равные промежутки времени тело проходит одинаковые пути, называется равномерным.

— А что означают слова «за любые равные промежутки времени»?

Ответим на этот вопрос, проведя следующий опыт. Возьмём вертикальную трубку, заполненную вязкой жидкостью, например, густым сахарным сиропом, и проследим за падением маленького металлического шарика в ней. Будем отмечать положение шарика через равные промежутки времени, например, через каждые 5 секунд.

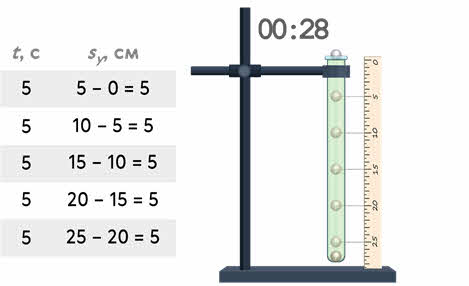
Не трудно заметить, что за равные промежутки времени, шарик совершает одинаковые перемещения.

Уменьшим промежутки времени, например, в два раза.

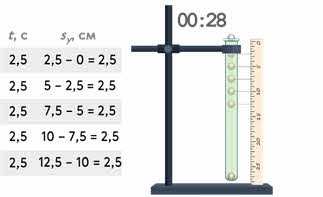
Как видим, во столько же раз уменьшаются и перемещения шарика, но по-прежнему за равные промежутки времени они будут равны.

Таким образом, равномерное прямолинейное движение — это такое движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Конечно же в реальной жизни очень трудно создать такие условия, чтобы тело двигалось равномерно в течение длительного промежутка времени. Поэтому равномерное движение является моделью реального движения тел.

Вы знаете, что в случае прямолинейного движения тела в одном направлении перемещение тела непрерывно возрастает. Чтобы найти перемещение за некоторый промежуток времени, надо знать, как быстро оно возрастает. Быстроту этого возрастания характеризует скорость.

Скорость равномерного прямолинейного движения — это векторная физическая величина, равная отношению перемещения к промежутку времени, за который оно совершено.

Скорость равномерного прямолинейного движения постоянна. Иными словами, с течением времени не изменяется ни её модуль, ни её направление.

Единицей скорости в СИ является метр в секунду. Скорость показывает, какое перемещение тело совершает в единицу времени.

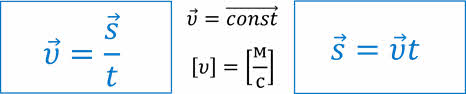
Так как векторная величина имеет не только числовое значение, но и направление, то по формулам, записанным в векторном виде, вычисления вести нельзя. Поэтому при вычислениях пользуются формулами, в которые входят не векторы, а их проекции на оси координат:

На прошлых уроках мы с вами говорили о том, что основной задачей механики является определение координаты тела в любой момент времени. Получим формулу для вычисления координаты тела для равномерного прямолинейного движения. Для этого рассмотрим равномерное движение лодки по прямолинейному участку реки.

Для описания движения лодки воспользуемся одной координатной осью, например Ox, выбрав в качестве начала отсчёта дерево на берегу реки. Лодку будем рассматривать как материальную точку.

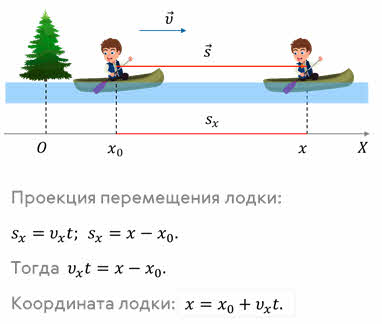
Полученное уравнение называется кинематическим законом движения или уравнением движения.

Из него следует, что для определения координаты движущегося тела в любой момент времени, необходимо знать его начальную координату и проекцию скорости движения на ось.

Необходимо помнить, что в формуле υ_х — это проекция вектора скорости. А она, как всякая проекция вектора, может быть больше или меньше нуля. Если направление движения совпадает с направлением оси Ох, то проекция скорости положительна. Если же направление вектора скорости противоположно направлению оси, то его проекция на эту ось отрицательна. Координата начального положения тела тоже может быть больше или меньше нуля, так как в момент начала наблюдения тело может находиться и по одну, и по другую стороны от начала отсчёта.

Для большей наглядности, движение можно описывать с помощью графиков. Рассмотрим, как строятся такие графики на конкретном примере. Саша и Маша идут навстречу друг к другу. Они движутся равномерно и прямолинейно. Модуль скорости Саши равен двум метрам в секунду, а Маши — одному метру в секунду.

Выберем координатную ось Ox, направив её в сторону движения Саши. Будем считать, что в момент начала наблюдения координата Саши равнялась 2 метрам, а Маши — 8 метрам. Построим графики зависимости проекции скорости движения Саши и Маши от времени. Для этого сначала найдём проекции их скоростей на координатную ось. При этом учтём, что направление вектора скорости Саши совпадает с направлением оси Ox, а Маши — нет. Так как скорости движения детей не меняются со временем, то графиками зависимости проекций их скоростей от времени будут прямые линии, параллельные оси времени.

По графику скорости можно определить перемещение тела за данный промежуток времени: при прямолинейном равномерном движении тела проекция вектора его перемещения численно равна площади прямоугольника, заключённого между графиком скорости, осью времени и перпендикулярами к этой оси, восставленными из точек, соответствующих моментам начала и конца наблюдения.

Теперь построим график проекции перемещения. Согласно формуле, проекция перемещения линейно зависит от времени, то есть графиком проекции перемещения является прямая линия. А направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.

По графику зависимости проекции перемещения тела от времени можно определить проекцию скорости тела, которая будет равна тангенсу угла наклона графика к оси времени.

Теперь разберёмся с график пути. Мы знаем, что при равномерном прямолинейном движении путь равен модулю перемещения. Поэтому график пути совпадает с графиком проекции перемещения, если проекция скорости положительна. И является «зеркальным отражением» от оси времени графика проекции перемещения, если проекция скорости отрицательна.

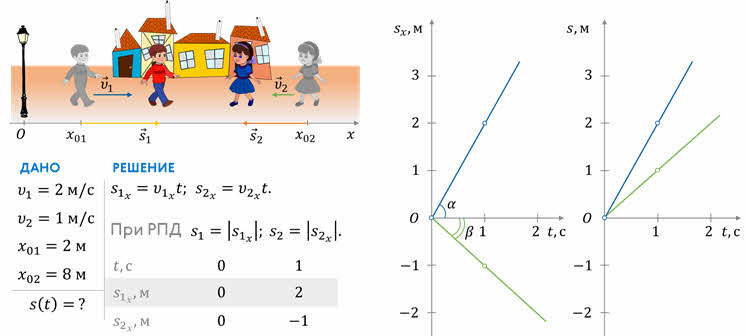
Ну и наконец рассмотрим график зависимости координаты тела от времени. Его также называют графиком движения. Для того, чтобы построить такой график, необходимо знать уравнение движения тела. Составим такие уравнения для Саши и Маши:

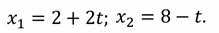
Из уравнений видно, что координаты Саши и Маши, при их равномерном прямолинейном движении, линейно зависят от времени. Построим графики координат, помня о том, что для построения прямой достаточно найти координаты двух любых её точек.

Для прямолинейного движения тела графики движения дают полное решение задачи механики, так как они позволяют найти координату тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному моменту.

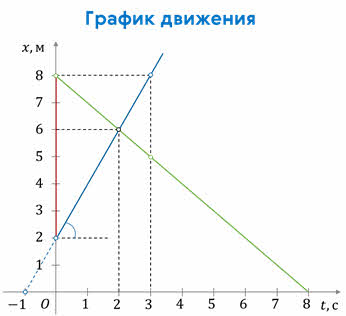
Так, например, продолжив график Саши в сторону, противоположную направлению его движения, увидим, что за секунду до начала наблюдения Саша находился в точке начала отсчёта координаты (конечно это будет справедливо только в том случае, если Саша двигался с такой же скоростью и до начала наблюдения).

По виду графиков движения можно судить и о скорости тел: чем круче график (то есть чем больше его угол наклона к оси времени), тем больше скорость движения.

Из графиков движения можно определить и перемещение тела за любой промежуток времени. Видно, например, что Саша, за первые 3 секунды движения совершил перемещение в положительном направлении оси Ох, по модулю равное 6 метрам.

А по точке пересечения графиков можно определить момент и координату встречи Саши и Маши, опустив перпендикуляры на соответствующие координатные оси.

Закрепление материала.

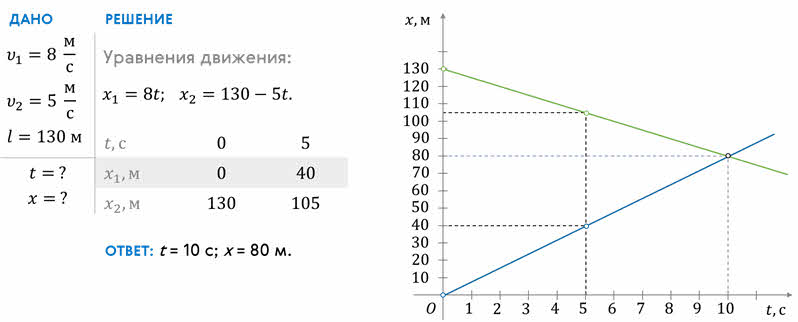
Две лодки плывут навстречу друг другу равномерно и прямолинейно. Скорость первой лодки 8 м/с, второй — 5 м/с. Определите время и координату их места встречи, если в начальный момент времени расстояние между лодками равно 130 метрам.