Определение координаты движущегося тела

На прошлом уроке мы с вами говорили о пути и перемещении тела. Давайте вспомним, что путь — это скалярная величина, равная длине траектории, которую описывает тело за некоторый промежуток времени.

А перемещением называется направленный отрезок прямой, соединяющий начальное и конечное положения тела.

Так как перемещение — это векторная величина, то есть имеет модуль и направление, то складывать и вычитать перемещения необходимо по правилам сложения и вычитания векторов. Однако при решении большинства задач, используется понятие не вектора, а проекции вектора на ось координат.

— А что такое проекция вектора и каковы её свойства?

На это вопрос мы с вами и попытаемся сегодня ответить. Начнём с простого — с понятия проекция точки на ось. Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.

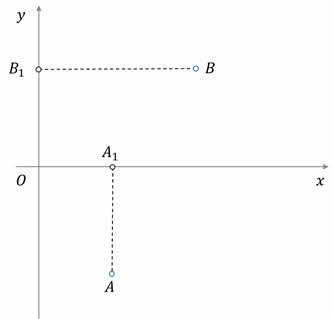
На представленном рисунке точка А₁ — это проекция точки А на ось Ox, а точка B₁ — проекция точки B на ось Oy.

Теперь разберёмся с проекцией вектора на ось. Согласно определению, проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора на эту ось, взятая со знаком «плюс» или «минус».

Знак «плюс» берут, если угол между вектором и осью острый, а «минус» — если угол тупой.

Обозначать проекцию вектора будем той же буквой, что и вектор, но с индексом внизу (например, a_x — это проекция вектора a на ось Ox).

— А если вектор перпендикулярен оси?

Тогда проекция этого вектора равна нулю.

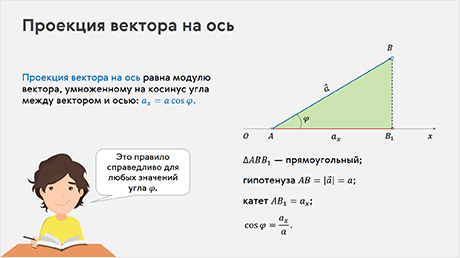
Проекцию вектора можно выразить через его модуль и угол между вектором и осью. Итак, пусть у нас есть вектор a направленный под некоторым острым углом к координатной оси Ox. Укажем проекцию этого вектора на ось.

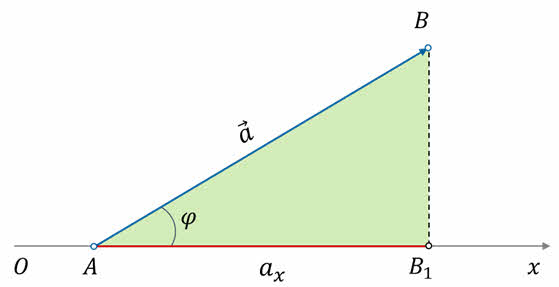
У нас с вами получился прямоугольный треугольник, гипотенуза которого равна длине вектора a, а катет AB₁ — это проекция вектора a на ось Ox.

Тогда, на основании определения косинуса острого угла, мы можем записать, что проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью:

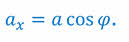
Это правило справедливо при любых значениях угла φ. Например, для углов, больше 90^о, косинус угла φ отрицательный. Тогда по формуле получается, что проекция вектора на ось также отрицательна, как и должно быть по определению проекции.

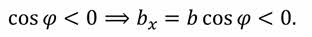
— А можно ли найти модуль и направление вектора по его проекциям на координатные оси?

Чтобы ответить на этот вопрос рассмотрим вектор, лежащий в плоскости xOy. Вектор, лежащий в заданной плоскости, определяется двумя проекциями на оси координат.

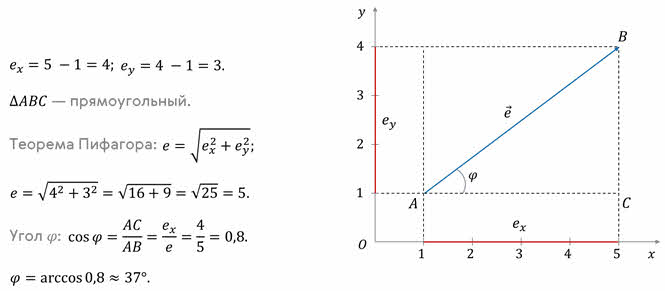
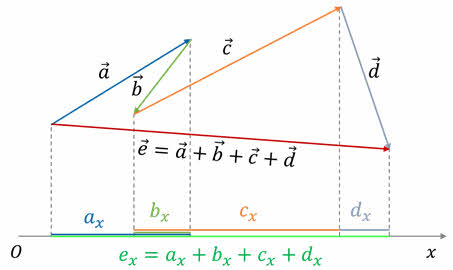
Обратим внимание на важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.

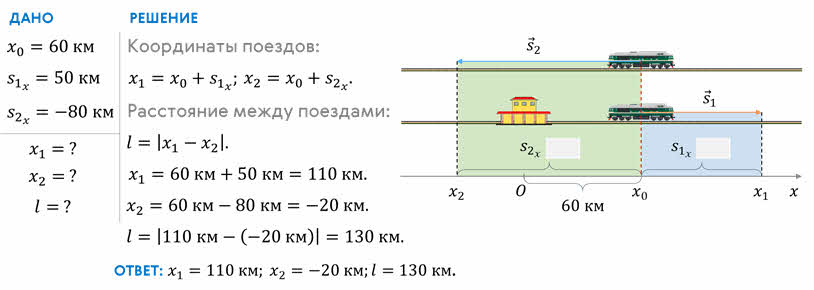
Но вернёмся к нашему прошлому уроку. На нём мы с вами говорили о том, что положение тела, которое совершило некоторое перемещение, можно найти графически. Для этого достаточно отложить вектор перемещения от начального положения этого тела. Однако в большинстве случаев необходимо уметь вычислять положение тела, то есть уметь определять его координаты. Давайте на примере решения задачи посмотрим, как можно определить координату движущегося тела, зная координату его начального положения и вектор перемещения.

Итак, два поезда идут по параллельным путям в противоположных направлениях и встречаются в шестидесяти километрах к востоку от железнодорожного вокзала. Продолжив движение через некоторое время t первый поезд удалился от места встречи на 50 километров в восточном направлении, а второй — на 80 километров в западном. Определите координаты каждого поезда относительно вокзала и расстояние между ними через промежуток времени t.