На уроках алгебры,
мы с вами уже знакомились с графиками некоторых функций. Давайте вспомним, как
выглядит, например, график линейной функции, график квадратичной функции,
график обратной пропорциональности, график функции  .
.
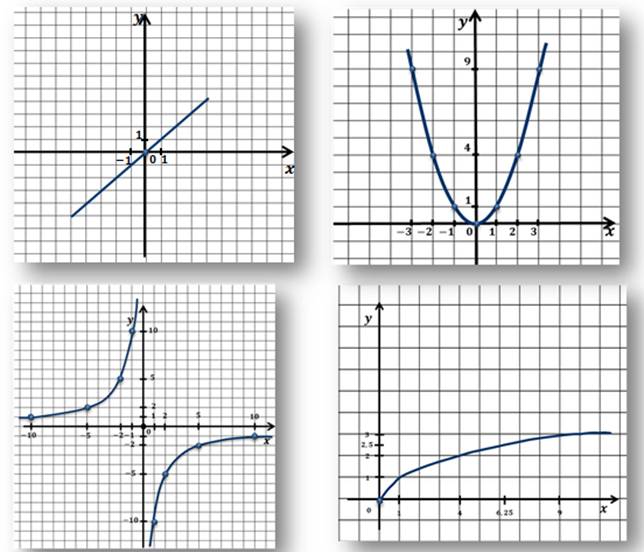
Давайте рассмотрим отдельно график линейной функции y= x. Если мы возьмем произвольные точки на этом графике, например, М1 и М2, то координаты этих точек будут удовлетворять следующему условию: x=y.

Это же условие будет выполняться для любой точки, лежащей на этой прямой. Но если мы возьмем любую точку вне этого графика, то координаты этой точки не будут удовлетворять условию: x=y. В таких случаях говорят, что уравнение y=x является уравнением прямой M1M2.
Теперь давайте попробуем ввести понятие уравнения для произвольной линии.

Пусть в декартовой системе координат дана произвольная линия l. Уравнение с двумя переменными x и y называется уравнением линии l, если этому уравнению удовлетворяют координаты любой точки линии l и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
Например, уравнением параболы, которая изображена на рисунке будет уравнение y=x2.

Для того, чтобы в этом убедится, давайте возьмем две точки: одну на параболе, вторую – вне параболы. Подставив координаты обеих точек в уравнение y=x2, мы увидим, что координаты точки, лежащей на параболе, удовлетворяют нашему уравнению, а координаты точки, которая не лежит на параболе – не удовлетворяют. Очевидно, что координаты всех точек, которые лежат на параболе, будут удовлетворять этому уравнению.
Давайте решим задачу.
Задача. Записать уравнение, которое задает линию:
Решение.








Ответ:  .
.
Рассмотрим еще один пример.
Задача. Записать уравнение, которое задает линию:

Решение.
По рисунку видно, что эта линия будет являться
графиком функции
 . По графику видно,
что он проходит например, через точку с
координатами (5;-2). Поскольку координаты этой точки должны удовлетворять
искомому уравнению, то подставим их в уравнение. Получим, что данную линию
задает уравнение
. По графику видно,
что он проходит например, через точку с
координатами (5;-2). Поскольку координаты этой точки должны удовлетворять
искомому уравнению, то подставим их в уравнение. Получим, что данную линию
задает уравнение


Ответ:  .
.
Задача. Построить
линию, которую задает уравнение  .
.
Решение.

Такие задания мы делали в курсе алгебры. Построим таблицу значений. Поскольку, это линейная функция, то достаточно взять две точки.
|
|
-1 |
0 |
|
|
-2 |
3 |


Задача. Построить
линию, которую задает уравнение  .
.
Решение.
|
|
-3 |
-2 |
1 |
6 |
13 |
|
|
0 |
1 |
2 |
3 |
4 |





Отметим получившиеся точки на координатной плоскости, соединим их плавной линией и получим кривую

Давайте подведем итоги нашего урока. Сегодня на уроке мы познакомились с таким понятием как уравнение линии. Уравнение с двумя переменными x и y называется уравнением линии l, если этому уравнению удовлетворяют координаты любой точки линии l и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

 Получите свидетельство
Получите свидетельство Вход
Вход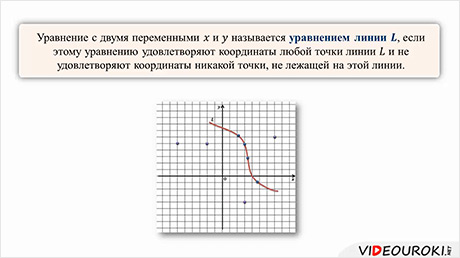







 0
0 6110
6110

