Прежде всего, давайте вспомним, формулу расстояния между двумя точками и еще, повторим, что уравнение с двумя переменными x и y называется уравнением линии l, если этому уравнению удовлетворяют координаты любой точки линии l и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
Сегодня на уроке мы попробуем по геометрическим свойствам линии найти ее уравнение.
В качестве линии
рассмотрим окружность радиуса 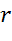 с
центром в точке
с
центром в точке 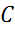 .
.
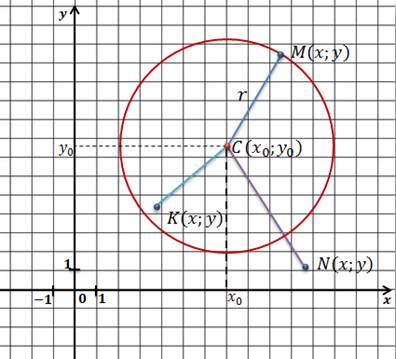
Пусть центр
окружности имеет координаты  . Возьмем на
окружности произвольную точку
. Возьмем на
окружности произвольную точку  . Запишем формулу
расстояния между точками C и M.
Мы знаем, что длина отрезка, который соединяет любую точку на окружности с
центром окружности – это радиус. Поэтому можно записать, что MC
равно r. Возведем MC в квадрат
и получим уравнение MC2 = r2.
Заменим MC2 квадрат на выражение
. Запишем формулу
расстояния между точками C и M.
Мы знаем, что длина отрезка, который соединяет любую точку на окружности с
центром окружности – это радиус. Поэтому можно записать, что MC
равно r. Возведем MC в квадрат
и получим уравнение MC2 = r2.
Заменим MC2 квадрат на выражение  и получим, что если
точка лежит на окружности с радиусом r и центром в
точке C, то координаты этой точки удовлетворяют
уравнению
и получим, что если
точка лежит на окружности с радиусом r и центром в
точке C, то координаты этой точки удовлетворяют
уравнению 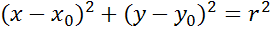 . Если точка не
лежит на окружности, то расстояние от этой точки до центра окружности не равно
радиусу, поэтому координаты таких точек не будут удовлетворять полученному
уравнению. Поэтому можно сказать, что в прямоугольной системе координат уравнение
окружности радиуса r с центром в точке C с координатами
. Если точка не
лежит на окружности, то расстояние от этой точки до центра окружности не равно
радиусу, поэтому координаты таких точек не будут удовлетворять полученному
уравнению. Поэтому можно сказать, что в прямоугольной системе координат уравнение
окружности радиуса r с центром в точке C с координатами  имеет вид:
имеет вид: 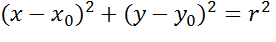 .
.
Задача. Записать
уравнение окружности с радиусом 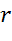 и центром в начале
координат.
и центром в начале
координат.
Решение.
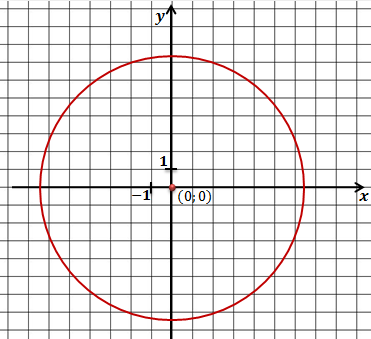
Начало координат имеет координаты (0;0). Подставим их в уравнение окружности и получим, что уравнение окружности с радиусом r и центром в начале координат имеет вид
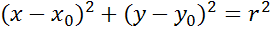
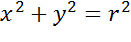 .
.
Задача. Начертить
окружность, заданную уравнением 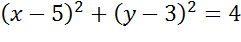 .
.
Решение.
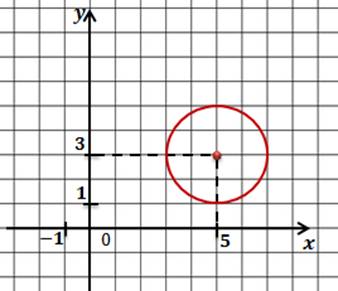
Запишем общее уравнение окружности и проанализируем исходное уравнение. Прежде всего, определимся с координатами центра окружности. Это будут числа 5 и 3. Теперь давайте определим величину радиуса окружности.
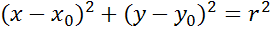
Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 4. Получим 2.
Значит наша формула задает окружность с центром в точке с координатами пять три и радиусом равным двум.
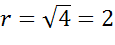
Задача. Начертить
окружность, заданную уравнением 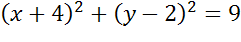 .
.
Решение.
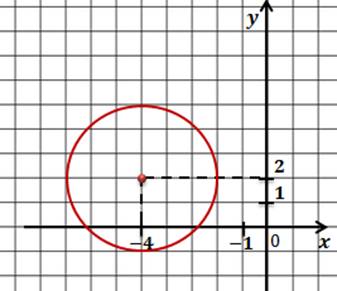
Запишем общее уравнение окружности и проанализируем исходное уравнение. Прежде всего определимся с координатами центра окружности.
Это будут числа -4 и 2. Теперь давайте определим величину радиуса окружности.
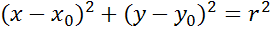
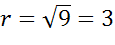
Задача. Начертить
окружность, заданную уравнением 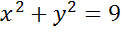 .
.
Решение. Уравнениями такого типа описываются окружности с центром в начале координат. Теперь давайте определим величину радиуса окружности. Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 9.
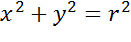
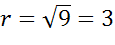
Значит наша формула задает окружность с центром в точке с координатами (0;0) и радиусом равным 3.
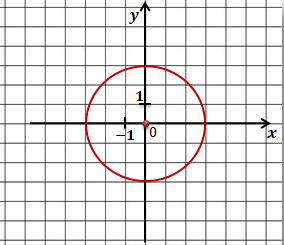
Теперь давайте попробуем решить задачу обратную данным.
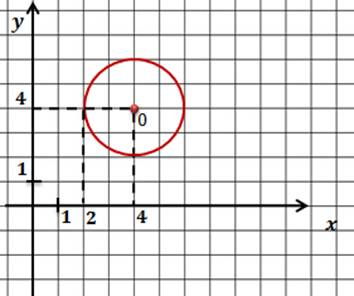
Задача. Составить уравнение окружности, которая показана на рисунке.
Как и в предыдущих задачах мы начнем с определения координат центра окружности. Сделать это нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр окружности имеет координаты (0;0).
Нетрудно заметить, что радиус окружности равен 4.
Запишем уравнение окружности и подставим найденные значения.
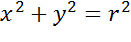
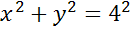
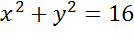
Ответ: 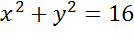 .
.
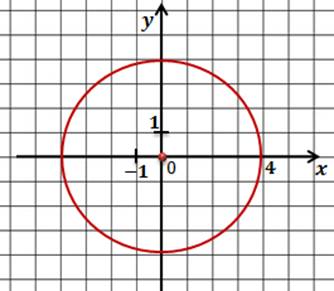
Решим еще одну задачу.
Задача. Составить уравнение окружности, которая показана на рисунке.
Решение.
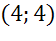 – центр окружности
– центр окружности
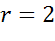 – радиус окружности
– радиус окружности
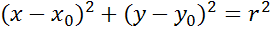
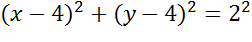
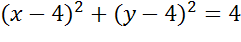
Ответ: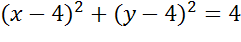 .
.
Задача. Составить уравнение окружности, которая показана на рисунке.
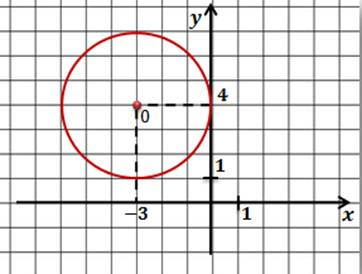
Решение.
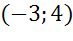 – центр окружности
– центр окружности
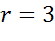 – радиус окружности
– радиус окружности
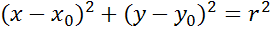
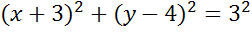
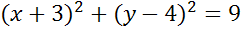
Ответ: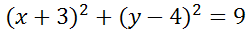 .
.
Решая задачи, мы с вами выполняли один и тоже порядок действий. Давайте еще раз повторим этот порядок.
Для того, что бы составить уравнение окружности и построить ее надо:
1. Найти координаты центра окружности.
2. Найти длину радиуса этой окружности.
3. Записать уравнение окружности.
4. Подставить полученные значения в уравнение окружности.
5. Построить окружность, если это требуется для решения задачи.
Рассмотрим еще одну задачу.
Написать уравнение окружности с диаметром эм эн, если точка эн имеет координаты два три, точка эм имеет координаты шесть три.
Задача. Написать
уравнение окружности с диаметром 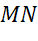 , если
, если 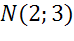 ,
, 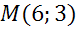 .
.
Решение.
Найдем координаты центра окружности. Центр окружности является серединой диаметра. Воспользуемся формулами для нахождения координат середины отрезка.
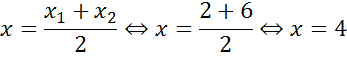
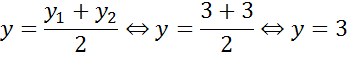
Получим, что центр
окружности имеет координаты 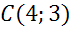 .
.
Теперь определим радиус окружности. Для этого найдем расстояние от центра окружности до концов диаметра.
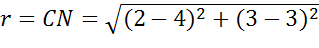
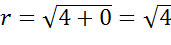
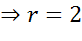
Запишем общее уравнение окружности и подставим в него найденные значения. Тогда получим, что уравнение данной окружности имеет вид:
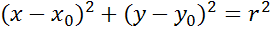
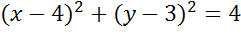
Ответ: 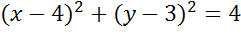 .
.
Подведем итоги урока.
На сегодняшнем уроке мы познакомились с формулой, которая задает окружность с центром в точке С (x0; y0) и радиусом r.
Также мы познакомились с формулой, которая задает окружность с центром в начале координат и радиусом r.
Мы рассмотрели задачи на составление уравнения окружности по рисунку и на построение окружности по заданному уравнению.

 Получите свидетельство
Получите свидетельство Вход
Вход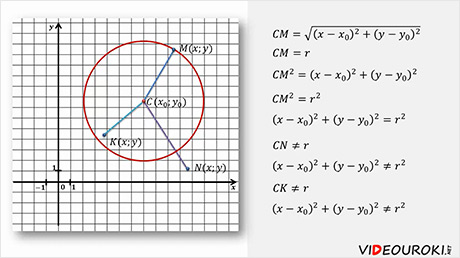



 0
0 21999
21999

