Прежде чем приступить к изучению нового материала, давайте повторим формулу для нахождения координат середины отрезка
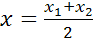 ,
,  , формулу для
определения расстояния между двумя точками
, формулу для
определения расстояния между двумя точками 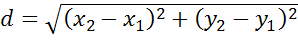 , вспомним, что
называется уравнением линии l, запишем уравнение
окружности с радиусом r и центром в точке C (x0;y0).
Вспомним уравнение окружности радиуса r и центром в
начале координат
, вспомним, что
называется уравнением линии l, запишем уравнение
окружности с радиусом r и центром в точке C (x0;y0).
Вспомним уравнение окружности радиуса r и центром в
начале координат 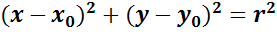 .
.
Сегодня на уроке мы выведем уравнение произвольной прямой l.
В координатной плоскости прямая может располагаться либо вертикально (параллельно оси Oy), горизонтально (параллельно оси Ox) либо быть наклонной к обеим осям.
Первым давайте рассмотрим случай, когда прямая параллельна оси Oy.
Возьмем на оси Ox, например, точку с координатой 3 и проведем через эту точку прямую, параллельную оси Oy. Абсцисса любой точки этой прямой равна 3. То есть координаты любой точки этой прямой удовлетворяют уравнению x=3, а координаты любой точки, которая не лежит на данной прямой не удовлетворяют данному уравнению. Значит, уравнение x=3 является уравнением прямой параллельной оси Oy и проходящей через точку с координатами (3;0).
Можно сказать, что
произвольная прямая параллельная оси Oy задается уравнением  . Уравнение
. Уравнение  является уравнением оси
является уравнением оси
 .
.
Задача. Записать уравнения прямых, показанных на рисунке:
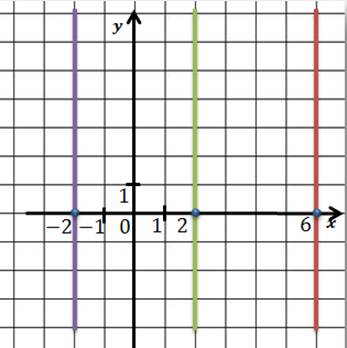
Решение.
Для того, чтобы записать уравнение каждой прямой, запишем общее уравнение прямых параллельных оси Oy.




Рассмотрим теперь случай когда прямая параллельна оси Ox.

Возьмем на оси Oy, например, точку 5 и проведем через нее прямую параллельную оси Ox. Любая точка этой прямой удовлетворяет уравнению y=5, любая точка, которая не лежит на этой прямой не удовлетворяет этому уравнению, значит, эту прямую задает уравнение y=5.
Можно сказать, что
произвольная прямая параллельная оси Ox задается уравнением  .Ось Ox
задается уравнением
.Ось Ox
задается уравнением  .
.
Задача. Записать уравнения прямых, показанных на рисунке:

Решение.
Запишем общее уравнение прямых параллельных оси Ox.
 .
.



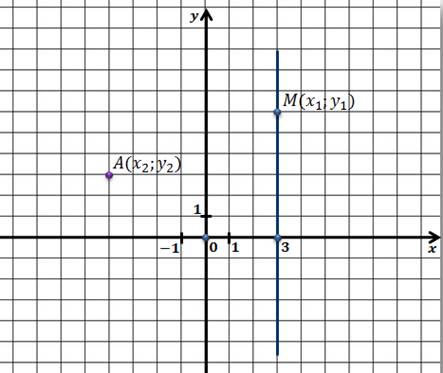
Теперь рассмотрим случай, когда прямая наклонная к обеим осям.
Отметим на координатной плоскости точки с координатами (x1; y1) и (x2; y2) так, чтобы указанная прямая l была серединным перпендикуляром к отрезку AB.

Теперь возьмем произвольную точку M (x;y). Если точка M лежит на прямой l, то, очевидно, что длины отрезков AM и BM будут равны. Найдем эти отрезки и приравняем их.


Получим уравнение:


Если точка M не лежит на прямой, то, очевидно, что отрезки AM и BM не будут равны и координаты точки M не будут удовлетворять этому уравнению.
Значит, в прямоугольной системе координат уравнение прямой l имеет вид:
 .
.
Раскроем скобки и выполним
элементарные преобразования.Введем замену.  ;
; 
Получим уравнение  .
.
Так как в самом
начале мы говорили, что точки A и B – различные точки, то хотя бы одна из разностей  ,
,  не равна нулю, то есть
хотя бы один из коэффициентов a и b
не равен нулю. То есть можно сказать, что уравнение прямой в прямоугольной
системе координат является уравнением первой степени и имеет вид:
не равна нулю, то есть
хотя бы один из коэффициентов a и b
не равен нулю. То есть можно сказать, что уравнение прямой в прямоугольной
системе координат является уравнением первой степени и имеет вид:  .
.
Задача. Написать
уравнение прямой, проходящей через точки  и
и  .
.
Решение.








Ответ: 
Предположим, что в этом уравнении коэффициент
 .
.



Тогда получим
уравнение  .
.
Число k называется угловым коэффициентом прямой.
Отметим, что две параллельные прямые, не параллельные оси Oy имеют одинаковые угловые коэффициенты и если две прямые имеют одинаковые угловые коэффициенты, то эти прямые параллельны.
Задача. Записать
угловой коэффициент прямой, проходящей через точки  и
и  .
.
Решение.
 d
d





Ответ: 
Задача. Среди
предложенных уравнений прямых выберите те, которые задают прямые, параллельные
прямой 
а)  б)
б)  в)
в)  г)
г)  .
.
Решение. Мы говорили, что две параллельные прямые имеют одинаковые угловые коэффициенты, поэтому искомыми уравнениями будут только уравнения

а) 
б) 
в) 
г) 
Ответ: б)  г)
г)  .
.
Задача. Укажите пары параллельных прямых
а)  и
и  б)
б)  и
и 
в)  и
и  .
.
Решение.
а) 

б) 

в) 

Ответ: б)  и
и  .
.
Задача. Даны
координаты вершин трапеции 
 . Написать
уравнения прямых, содержащих диагонали
. Написать
уравнения прямых, содержащих диагонали  .
.
Решение.
Запишем общее уравнение прямой  .
.






Аналогично найдем, что уравнение прямой, которая содержит диагональ BD имеет вид y=1.







Ответ:  .
.
Давайте подведем итоги урока.
Уравнение прямой
имеет вид:  . Еще один вид уравнения
прямой –
. Еще один вид уравнения
прямой –  –
угловой коэффициент прямой.
–
угловой коэффициент прямой.
Уравнение прямой,
параллельной оси Ox имеет вид  . Уравнение прямой,
параллельной оси Oy имеет вид
. Уравнение прямой,
параллельной оси Oy имеет вид  .
.
Две параллельные прямые, не параллельные оси о игрек имеют одинаковые угловые коэффициенты и если две прямые имеют одинаковые угловые коэффициенты, то эти прямые параллельны.

 Получите свидетельство
Получите свидетельство Вход
Вход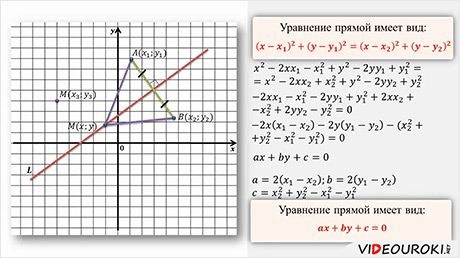



 0
0 23143
23143

