Практическая работа
Тема: «Вычисление пределов функции»
Цель: сформировать умение находить пределы функций, использовать замечательные пределы для нахождения пределов.
Теоретические сведения к практической работе.
Число А называют пределом функции f(x) при ![]() (и пишут
(и пишут ![]() ), если для любого
), если для любого ![]() найдется число
найдется число ![]() зависящее от , такое, что для всех
зависящее от , такое, что для всех ![]() , удовлетворяющих условию
, удовлетворяющих условию ![]() , выполняется неравенство
, выполняется неравенство ![]()
Теоремы о пределах:
1. ![]() (c=const).
(c=const).
2. Если ![]() то:
то:
![]()
![]()
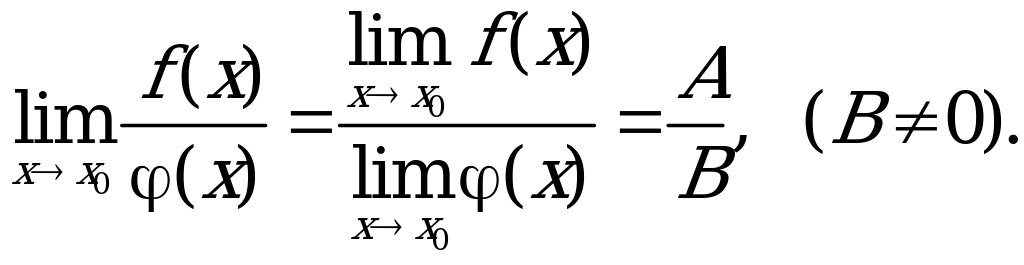
Первый замечательный предел: ![]()
Второй замечательный предел (число е = 2,718…):
![]() или
или ![]()
Замечательные пределы:
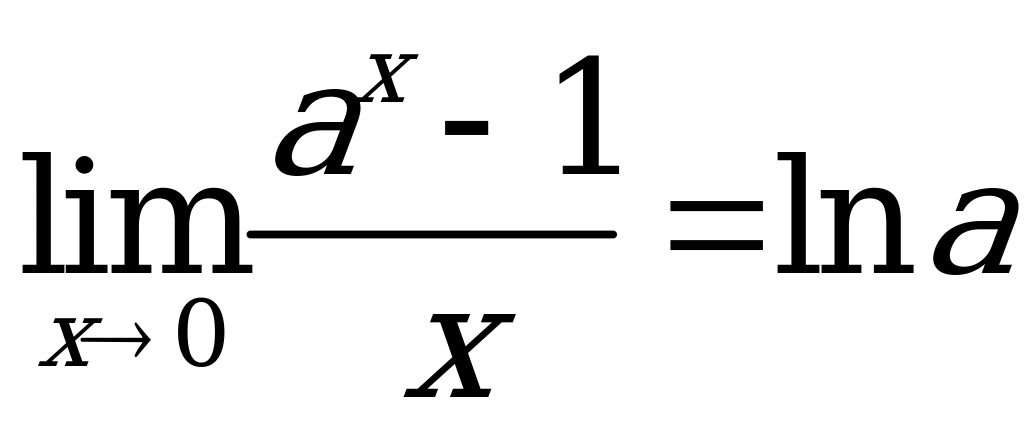
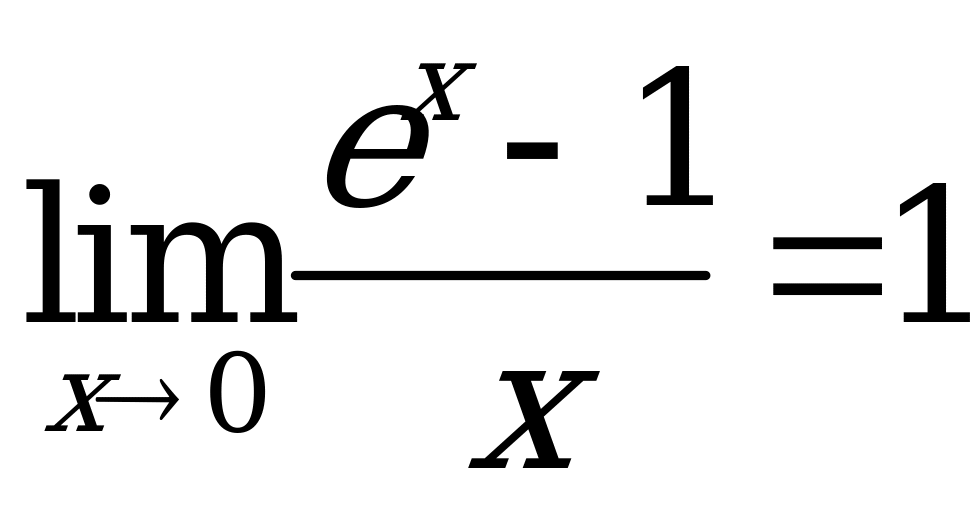
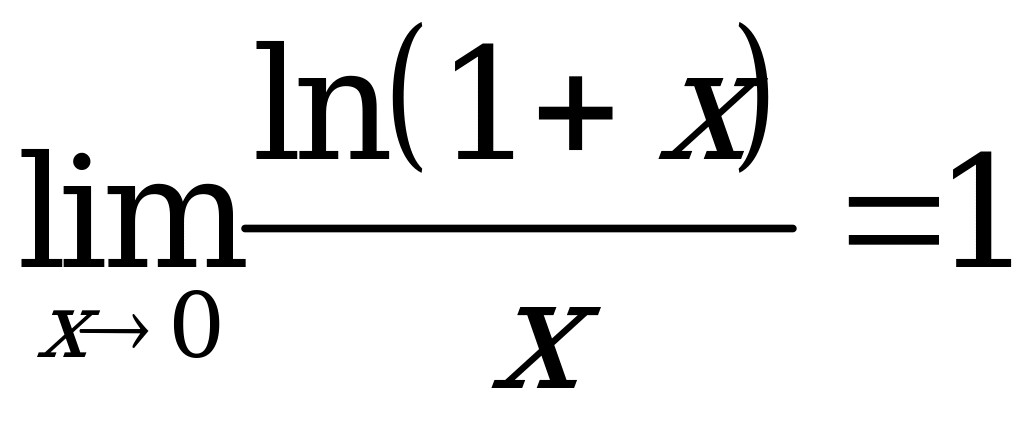
![]()
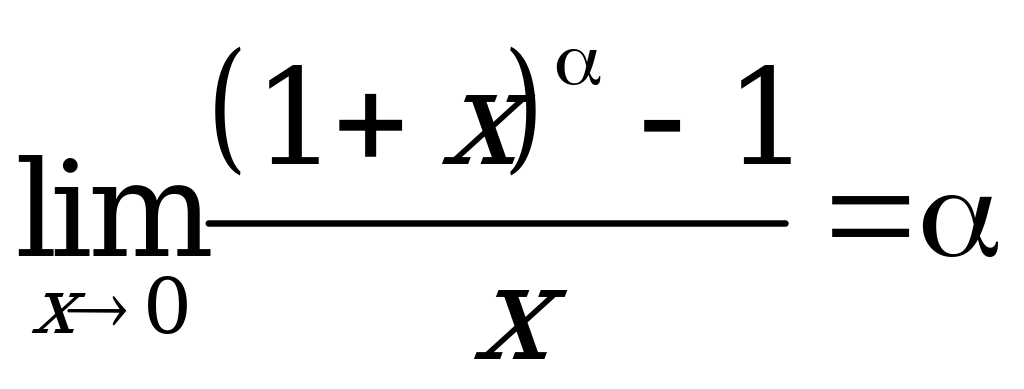
Примеры решения:
![]()
Когда дан любой предел, сначала просто пытаемся подставить число в функцию
1)Пределы с неопределенностью вида ![]() и метод их решения
и метод их решения
1) деление на х в старшей степени:
Пример 1:
![]()
![]()
Сначала мы смотрим на числитель и находим ![]() в старшей степени:
в старшей степени:
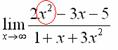
Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим ![]() в старшей степени:
в старшей степени:
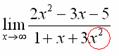
Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность ![]() необходимо разделить числитель и знаменатель на
необходимо разделить числитель и знаменатель на ![]() в старшей степени.
в старшей степени.
![]() Разделим числитель и знаменатель на
Разделим числитель и знаменатель на ![]()

П ![]() ример 2:
ример 2:
Найти предел
Снова в числителе и знаменателе находим ![]() в старшей степени:
в старшей степени:
![]()
Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Разделим числитель и знаменатель на ![]()
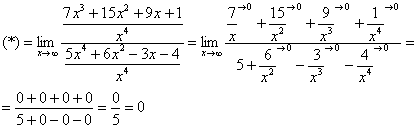
П ![]() ример 3
ример 3
Найти предел
Разделим числитель и знаменатель на ![]()
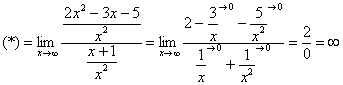
при раскрытии неопределенности вида ![]() у нас может получиться конечное число, ноль или бесконечность.
у нас может получиться конечное число, ноль или бесконечность.
2. Пределы с неопределенностью вида ![]() и метод их решения
и метод их решения
1) разложение числителя и знаменателя на множители.
Пример 4
![]()
Разложим числитель и знаменатель на множители
Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:
![]()
Сначала находим дискриминант:
![]()
И квадратный корень из него: ![]() Далее находим корни:
Далее находим корни: ![]()
![]() Таким образом:
Таким образом: ![]()
Всё. Числитель на множители разложен.
Знаменатель. Знаменатель ![]() уже является простейшим множителем, и упростить его никак нельзя.
уже является простейшим множителем, и упростить его никак нельзя.
![]() можно сократить на
можно сократить на ![]() :
:
![]() Теперь и подставляем -1 в выражение, которое осталось под знаком предела:
Теперь и подставляем -1 в выражение, которое осталось под знаком предела: ![]()
![]()
2) умножение числителя и знаменателя на сопряженное выражение.
П ![]() ример 5
ример 5
Найти предел
Умножаем числитель и знаменатель на сопряженное выражение: ![]()
Применяем вверху формулу ![]() :
: 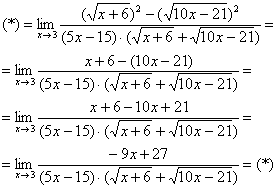 Неопределенность
Неопределенность ![]() не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:
не пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:
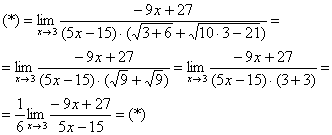
Число, как уже отмечалось ранее, лучше вынести за значок предела.
Теперь осталось разложить числитель и знаменатель на множители и сократить «виновников» неопределённости, ну а предел константы – равен самой константе:
![]()
Решение данного примера в чистовом варианте выглядит так:
![]()
Умножим числитель и знаменатель на сопряженное выражение.
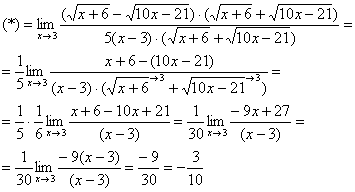
![]()
3) использование 1-го замечательного предела
П ![]() ример 6
ример 6
Найти предел
Выражение под знаком предела похоже на первый замечательный предел, но это не совсем он, под синусом находится ![]() , а в знаменателе
, а в знаменателе ![]() .В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом 7х, значит, в знаменателе тоже нужно получить 7х».
.В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом 7х, значит, в знаменателе тоже нужно получить 7х».
А делается это очень просто:
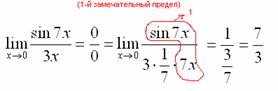
Пример 7
Найти предел

Пример 8
Найти предел

Пример 9
Найти предел

Пример 10
Найти предел
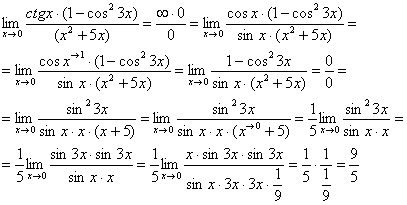

 Получите свидетельство
Получите свидетельство Вход
Вход











 Вычисление пределов функции (297.9 KB)
Вычисление пределов функции (297.9 KB)
 0
0 182
182 0
0 Нравится
0
Нравится
0








