Методические указания по выполнению практических работ по математике

Содержание

Пояснительная записка  4

Раздел 1. Уравнения, неравенства, системы уравнений и неравенств           

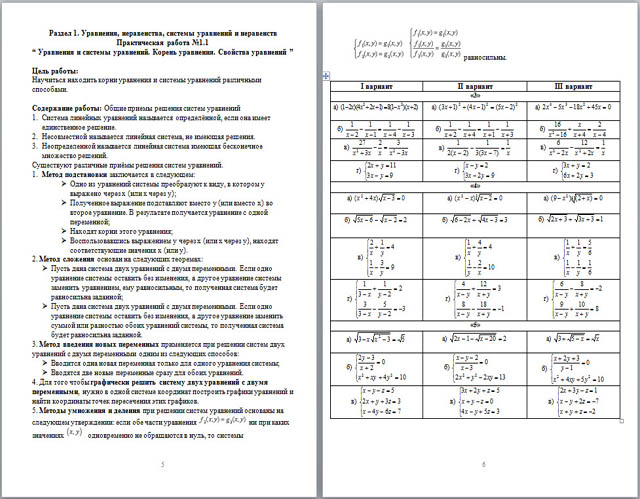
1.1 Уравнения и системы уравнений. Корень уравнения. Свойства уравнений  5

1.2 Неравенство и системы неравенств. Решение неравенство. Свойства неравенств  7

1.3 Определители ІІ и ІІІ порядков. Решение систем двух (трех) уравнений по формуле Крамера 10

Раздел 2.Функции, их свойства и графики         

2.1 Числовая функция. Способы задания функции. График функции. Свойства функции  12

2.2 Предел функции в точке. Основные свойства предела  14

Раздел 3. Показательная, логарифмическая и степенная функции     

3.1 Логарифмы. Решение простейших и сводящихся к ним логарифмических уравнений и неравенств  17

3.2 Решение простейших и сводящихся к ним показательных уравнений и неравенств  20

Раздел 4. Тригонометрические функции 

4.1 Решение тригонометрических уравнений  22

4.2 Решение тригонометрических неравенств  28

4.3 Тождественные преобразования тригонометрических выражений  30

Раздел 5. Векторы и координаты  

5.1 Понятие вектора. Действия с векторами  32

5.2 Уравнения прямой. Уравнения прямой, проходящий через одну точку, через две точки. Угол между прямыми  37

Раздел 6. Производная и ее приложения 

6.1 Производные суммы, произведения и частного двух функций. Правило дифференцирования сложной функции  41

6.2 Производные тригонометрических функций, обратных тригонометрических функций  43

6.3 Производные степенной, показательной, логарифмической функций  45

6.4 Применение производной к построению графиков функции  47

Раздел 7. Первообразная функция и интеграл    

7.1 Первообразная. Неопределенный интеграл и его свойства  51

7.2 Определенный интеграл. Основные свойства и вычисление определенного интеграла  54

Пояснительная записка

Методические указания предназначены для проведения практических работ по дисциплине "Математика" учащихся первого курса (для всех специальностей колледжа).

Содержание практических работ позволяет освоить:

методы и способы решения систем уравнений;

методы и способы решения систем неравенств;

исследование графиков функции;

практические приемы вычисления пределов;

виды и методы решения простейших логарифмических уравнений и неравенств;

виды и методы решения простейших показательных уравнений и неравенств;

виды и методы решения тригонометрических уравнений и неравенств;

различные способы задания прямой;

практические приемы нахождения частных производных функций многих переменных;

исследование функции с помощью производной;

практические приемы вычисления с помощью методов интегрального исчисления;

В методических указаниях к выполнению практических работ содержится инструкция с четким алгоритмом хода работы. Каждая практическая работа включает краткий теоретический материал, примеры задач и разноуровневый набор заданий. Выполнение практической работы помогает сконцентрировать внимание на главных проблемах изучаемого материала, способствуют развитию зрительной памяти, развивают навыки самостоятельной работы с материалом и закрепляют полученные знания.

Методические указания могут быть использованы для самостоятельной работы студентов.

Ход выполнения практической работы

Практические работы необходимо выполнять в специальных тетрадях с указанием номера, темы, целей работы.

Познакомиться с теоретическим материалом

Сделать краткий конспект теоретического материала в рабочих тетрадях (основные понятия, определения, формулы, примеры)

В тетрадях для практических работ выполнить задания по варианту.

Сдать преподавателю тетради для практических работ.

Критерии оценивания практических работ

Оценка «5» ставится, если верно и рационально решено 90%-100% предлагаемых заданий, допустим 1 недочет, неискажающий сути решения.

Оценка «4» ставится при  безошибочном решении 80% предлагаемых заданий.

Оценка «3» ставится, если выполнено 70% предлагаемых заданий, допустим 1 недочет.

Оценка «2» - решено мене 50% предлагаемых заданий.

Раздел 4. Тригонометрические функции

Практическая работа №4.3

“Тождественные преобразования тригонометрических выражений”

В тождественных преобразованиях тригонометрических выражений могут быть использованы следующие алгебраические приемы: добавление и вычитание одинаковых слагаемых; вынесение общего множителя за скобки; умножение и деление на одну и ту же величину; применение формул сокращенного умножения; выделение полного квадрата; разложение квадратного трехчлена на множители; введение новых переменных с целью упрощения преобразований.

При преобразованиях тригонометрических выражений, содержащих дроби,  можно использовать свойства пропорции, сокращение дробей или приведение дробей к общему знаменателю. Кроме того, можно пользоваться выделением целой части дроби, умножением числителя и знаменателя дроби на одинаковую величину, а так же по возможности учитывать однородность числителя или знаменателя. При необходимости можно представлять дробь в виде суммы или разности нескольких более простых дробей.

Кроме того, применяя все необходимые методы преобразования тригонометрических выражений, необходимо постоянно учитывать облась допустимых значений преобразуемых выражений.

Пример 1.Вычислить А = (sin(2x – π)cos(3π – x)+sin(2x – 9π/2)cos(x+ π/2))²+(cos(x–π/2)cos(2x–7π/2) + sin (3π/2 – x) · sin (2x – 5π/2))²

Решение.

Из формул приведения следует:

sin (2x – π) = -sin 2x; cos (3π – x) = -cos x;

sin (2x – 9π/2) = -cos 2x; cos (x + π/2) = -sin x;

cos (x – π/2) = sin x; cos (2x – 7π/2) = -sin 2x;

sin (3π/2 – x) = -cos x; sin (2x – 5π/2) = -cos 2x.

Откуда в силу формул сложения аргументов и основного тригонометрического тождества получаем

А = (sin2xcosx + cos2xsinx)² +(-sinxsin2x + cosxcos2x)² = sin² (2x + x) + cos² (x+2x) = sin² 3x + cos² 3x = 1

Ответ: 1.

Основными приемами доказательства тригонометрических  тождеств являются:

а) сведение левой части тождества к правой путем соответствующих преобразований;

б) сведение правой части тождества к левой;

в) сведение правой и левой частей тождества к одному и тому же виду;

г) сведение к нулю разности левой и правой частей доказываемого тождества.

Пример 4.

Проверить, что cos 3x = -4cos x · cos (x + π/3) · cos (x + 2π/3).

Решение.

Преобразуя правую часть этого тождества по соответствующим тригонометрическим формулам, имеем

-4cosxcos(x + π/3)cos(x + 2π/3) = -2cosx(cos((x + π/3) + (x + 2π/3)) + cos ((x + π/3) – (x + 2π/3))) = -2cos x · (cos (2x + π) + cos π/3) = 2cos xcos 2x - cos x = (cos3x + cos x) – cos x = cos 3x.

Правая часть тождества сведена к левой.

Весь материал - смотрите документ.