Согласовано:________________
зам. директора по УР Л.В.Зуенок
«____» _____________2015г.
Утверждено:____________
Директор школы Л.В. Щеблыкина
приказ по школе № 381
от «28» августа 2015г.
Муниципальное бюджетное общеобразовательное учреждение
«Ваховская общеобразовательная средняя школа»
Нижневартовский район
Рабочая программа и календарно-тематическое планирование
по алгебре и началам математического анализа
для учащихся 10 класса
(базовый уровень)
Разработала:
учитель математики
Ахунова З.Н.
Рассмотрено на заседании МО
Протокол №_____ от _________ 2015г
Руководитель МО _________ В.В.Шулятьев
Ваховск
2015г
II. Пояснительная записка
Рабочая программа к учебному курсу «Алгебра и начала математического анализа » 10 класс составлена на основе:
Закона РФ «Об образовании в РФ» от 29.12.2012 № 273-ФЗ;
федерального компонента государственного образовательного стандарта (приказ Министерства образования Российской Федерации № 1089 от 05.03.2004 "Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования");
федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на текущий учебный год;
учебного плана на 2015-2016 учебный год;
Примерной и авторской программы основного общего образования по математике. Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа 10-11 классы / авт.- сост. И.И. Зубарева, А.Г. Мордкович – 2-е изд., испр. и доп. – М.: Мнемозина, 2014. – 63 с.).
Учебно – методический комплект для изучения курса алгебры и начал математического анализа в 10-м классе на базовом и углубленном уровнях соответствует требованиям ФГОС среднего общего образования. В данном курсе особенный стиль изложения, здесь реализуются развивающие концепции математического моделирования и математического языка. Этот комплект – естественное продолжение курса алгебры основной школы.
Изложение материала в учебнике дается подробно и обстоятельно. Во многих случаях весь материал невозможно раскрыть на уроке, поэтому некоторые темы даются ученикам для домашнего чтения и самостоятельного изучения. Эти темы обсуждаются на следующем уроке в классе – в форме беседы.
Если сравнить этот учебник с учебником для общеобразовательной школы (Алгебра и начала математического анализа. В 2-х ч. Ч.1. Учебник (базовый уровень) – М.: Мнемозина, 2013), то главы 3,4 , 5, 7 настоящего учебника во многом текстуально совпадают с главами 1-4 упомянутого учебника. Остальные четыре главы данного учебника являются новыми. Главы 1 и 2 носят характер повторения и расширения известного из курса алгебры основной школы материала о действительных числах и числовых функциях, глава 6 посвящена комплексным числам, а глава 8 – элементам теории вероятностей.
Данный учебно-методический комплект полностью соответствует требованиям подготовки учащихся к ЕГЭ по математике. Для составления данной рабочей программы воспользовалась авторской программой А. Г. Мордковича для общеобразовательных учреждений (базовый и углубленный уровни) к учебнику «Алгебра и начала математического анализа» /I вариант-4 часа в неделю / М. Мнемозина, 2014 гг. Так как, согласно действующему в школе учебному плану, в 10 классе базового уровня предполагается обучение в объеме 105 часов (3 часа в неделю), то количество уроков по некоторым разделам меньше, чем в авторской программе. Глава 6 имеет ознакомительный характер, поэтому к изучению этой темы не отведено часов. Более подробная расстановка часов указана в учебно – тематическом плане.
Изучение математики на базовом уровне среднего (полного) общего образования
направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
На основании требований Государственного образовательного стандарта 2004 г. в содержании календарно-тематического планирования предполагается реализовать актуальные в настоящее время компетентностный, личностно - ориентированный, деятельностный подходы, которые определяют задачи обучения:
приобретение математических знаний и умений;
овладение обобщенными способами мыслительной, творческой деятельностей;
освоение компетенций (учебно-познавательной, коммуникативной, рефлексивной, личностного саморазвития, ценностно-ориентационной) и профессионально-трудового выбора.
С учетом уровневой специфики класса выстроена система учебных занятий (уроков), спроектированы цели, задачи, ожидаемые результаты обучения (планируемые результаты), что представлено в схематической форме ниже.
Основой целью является обновление требований к уровню подготовки выпускников в системе естественно математического образования, отражающее важнейшую особенность педагогической концепции государственного стандарта – переход от суммы «предметных результатов» (то есть образовательных результатов, достигаемых в рамках отдельных учебных предметов) к межпредметным и интегративным результатам. Такие результаты представляют собой обобщенные способы деятельности, которые отражают специфику не отдельных предметов, а ступеней общего образования. В государственном стандарте они зафиксированы как общие учебные умения, навыки и способы человеческой деятельности, что предполагает повышенное внимание к развитию межпредметных связей курса алгебры и начал анализа.
Стандарт ориентирован на воспитание школьника – гражданина и патриота России, развитие духовно-нравственного мира учащегося, его национального самосознания. Эти положения нашли отражение в содержании уроков. В процессе обучения должно быть сформировано умение формулировать свои мировоззренческие взгляды и на этой основе – воспитание гражданственности и патриотизма.
Особенности организации учебного процесса
Важную роль в учебном процессе играют формы организации обучения или виды обучения, в качестве которых выступают устойчивые способы организации педагогического процесса.
Основной формой организации учебно-воспитательной работы с учащимися является урок (урок ознакомления с новым материалом, урок закрепления изученного, урок применения знаний и умений, урок обобщения и систематизации знаний, урок проверки и коррекции знаний и умений, комбинированный урок). Применение разнообразных, нестандартных форм обучения должно в первую очередь соответствовать интеллектуальному уровню развития обучающихся и их психологическим особенностям.
К нестандартным формам обучения математики в школе относятся: лекции, семинары, консультации, экскурсии, конференции, практикумы, деловые игры, дидактические игры, уроки-зачеты, работа в группах.
Не менее важны и формы контроля знаний, умений, навыков (текущий контроль, диагностический, рубежный, итоговый). Формы такого контроля также различны. Это могут быть и контрольные работы, и самостоятельные домашние работы, и защита рефератов и проектов, индивидуальное собеседование, диагностические работы, а также комплексное собеседование и защита темы.
Для развития у учащихся интереса к изучаемому предмету и, как следствие, повышения качества знаний используется современные инновационные технологии такие, как:
Технология уровневой дифференциации обучения
Технология проблемно-развивающего обучения
Здоровье-сберегающие технологии
Технологии сотрудничества
Содержание и объем курса
Согласно действующему в школе учебному плану календарно-тематический план предусматривает следующий вариант организации процесса обучения: в 10 классе базового уровня предполагается обучение в объеме 105 часов (3 часа в неделю).
На проведение текущих контрольных работ отведено 10 часов, в том числе и на проведение промежуточной итоговой контрольной работы. 2-х часовая контрольная работа, предложенная в авторском планировании в качестве итоговой контрольной работы, заменена Тестовой итоговой контрольной работой за курс 10 класса, которая проводится как промежуточная.
Формы и средства контроля:
Для проведения контрольных работ используется материалы из сборника Александрова Л. А., под ред. А.Г.Мордковича. Алгебра и начала анализа. 10 класс. Контрольные работы - М.: Мнемозина 2010 г.
Контрольные работы
|
№ |
Темы контрольных работ | Дата проведения |
| 1 | Входной срез. | 09.09.15 |
| 2 | Действительные числа. | 30.09.15 |
| 3 | Числовые функции. | 21.10.15 |
| 4 | Определение тригонометрических функций. | 25.11.15 |
| 5 | Тригонометрические функции (за 1 полугодие). | 21.12.15 |
| 6 | Тригонометрические уравнения (двухчасовая). | 20.01.16 20.01.16 |
| 7 | Преобразование тригонометрических выражений (двухчасовая). | 02.03.16 02.03.16 |
| 8 | Правила и формулы отыскания производных (двухчасовая). | 13.04.16 13.04.16 |
| 9 | Применение производной к исследованию функций (двухчасовая). | 04.05.16 04.05.16 |
| 10 | Итоговая контрольная работа (двухчасовая). | 25.05.16 25.05.16 |
III. Требования к уровню подготовки десятиклассников
В результате изучения математики на базовом уровне ученик должен
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира;
Алгебра
уметь:
– выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
– проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
– вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
– для практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
уметь:
– определять значение функции по значению аргумента при различных способах задания функции;
– строить графики изученных функций;
– описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
– решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
Начала математического анализа
уметь:
– вычислять производные и первообразные элементарных функций, используя справочные материалы;
– исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
– вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
– для решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Уравнения и неравенства
уметь:
– решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
– составлять уравнения и неравенства по условию задачи;
– использовать для приближенного решения уравнений и неравенств графический метод;
– изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
– для построения и исследования простейших математических моделей;
Элементы комбинаторики, статистики и теории вероятностей
уметь:
– решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
– вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
– для анализа реальных числовых данных, представленных в виде диаграмм, графиков;
– анализа информации статистического характера;
владеть компетенциями:
– учебно-познавательной, ценностно-ориентационной, рефлексивной, коммуникативной, информационной
IV. Учебно – тематический план
| Наименование раздела | Количество часов в авторской программе (I вар. – 4 часа в неделю) | Количество часов в рабочей программе (баз. ур. - 3 часа в неделю) |
| Повторение курса алгебры 9 класса. | 4 | 4 |
| Действительные числа. | 12 | 10 |
| Числовые функции. | 9 | 9 |
| Тригонометрические функции. | 24 | 21 |
| Тригонометрические уравнения. | 10 | 9 |
| Преобразование тригонометрических выражений. | 21 | 18 |
| Комплексные числа. | 9 | - |
| Производная. | 29 | 24 |
| Комбинаторика и вероятность. | 7 | 3 |
| Обобщающее повторение. | 11 | 7 |
| ИТОГО | 136 | 105 |
V. Содержание курса
Повторение курса алгебры 9 класса. (4ч)
Преобразование рациональных выражений. Числовые функции. Решение рациональных неравенств и их систем.
Действительные числа. (10ч)
Натуральные и целые числа. Делимость натуральных чисел. Признаки делимости. Простые и составные числа. Деление с остатком. НОД НОК нескольких натуральных чисел. Рациональные и иррациональные числа. Действительные числа и числовая прямая. Числовые промежутки. Модуль действительного числа. Построение графиков функций, содержащих модуль.
Числовые функции. (9ч)
Определение и способы задания числовой функции. Область определения и область значений функции. Свойства функций. Исследование функций. Чтение графика. Определение и задание обратной функции. Построение графиков прямой и обратной функции.
Тригонометрические функции. (21ч)
Числовая окружность. Длина дуги числовой окружности. Числовая окружность на координатной плоскости. Определение синуса и косинуса на единичной окружности. Определение тангенса и котангенса. Тригонометрические функции числового аргумента. Упрощение тригонометрических выражений. Тригонометрические функции углового аргумента. Решение прямоугольных треугольников. Формулы приведения. Функция y=sin x, её свойства и график. Функция y=cos x, её свойства и график. Периодичность функций y=sin x, y=cos x. Построение графика функций y=mf(x) и y=f(kx) по известному графику функции y=f(x). Функции y=tg x и y=ctg x, их свойства и графики.
Тригонометрические уравнения. (9ч)
Определение и вычисление арккосинуса. Решение уравнения cos t=a. Определение и вычисление
арксинуса. Решение уравнения sin t=a. Арктангенс и арккотангенс. Решение уравнений tg x=a, ctg x=a. Простейшие тригонометрические уравнения. Различные методы решения уравнений.
Однородные тригонометрические уравнения.
Преобразование тригонометрических выражений. (18ч)
Синус и косинус суммы и разности аргументов. Тангенс суммы и разности аргументов.
Формулы двойного аргумента. Преобразование сумм тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в суммы.
Производная. (24ч)
Числовые последовательности и их свойства. Предел последовательности. Сумма бесконечной геометрической прогрессии. Предел функции на бесконечности. Предел функции в точке. Приращение аргумента. Приращение функции. Определение производной. Производная и график функции. Производная и касательная. Формулы для вычисления производных. Производная сложной функции. Применение производной для исследования функций на монотонность и экстремумы.
График функции, график производной. Применение производной для исследования функций. Построение графиков функций. Задачи с параметром. Графическое решение.
Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на отрезке.
Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке. Текстовые и геометрические задачи на отыскание наибольших и наименьших значений величин.
Комбинаторика и вероятность. (3ч)
Правило умножения. Комбинаторные задачи. Перестановка и факториалы. Выбор нескольких элементов. Формула Бинома-Ньютона. Биноминальные коэффициенты. Треугольник Паскаля. Случайные события.
Обобщающее повторение. (7ч)
Решение тригонометрических уравнений методом введения новой переменной. Решение однородных тригонометрических уравнений. Решение тригонометрических уравнений с применением преобразования выражения.
Применение производной для исследования функции. Итоговая контрольная работа. Решение задач по всему курсу.
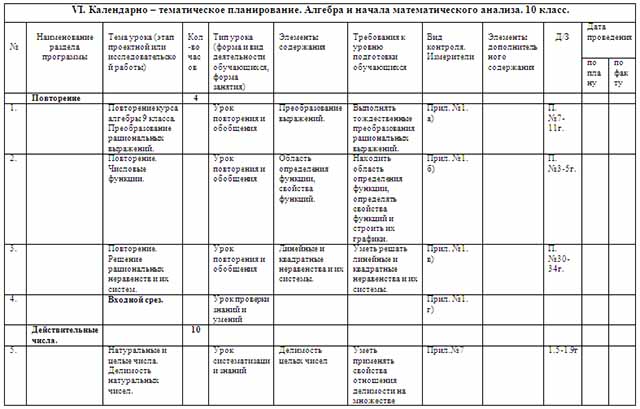
| VI. Календарно – тематическое планирование. Алгебра и начала математического анализа. 10 класс. |
|
№ |
Наименование раздела программы |
Тема урока (этап проектной или исследовательской работы) |
Кол-во часов |
Тип урока (форма и вид деятельности обучающихся, форма занятия) |
Элементы содержания |
Требования к уровню подготовки обучающихся |
Вид контроля. Измерители |
Элементы дополнительного содержания |
Д/З | Дата проведения |
| по плану | по факту |
|
| Повторение |
| 4 |
|
|
|
|
|
|
|
|
| 1. |
| Повторение курса алгебры 9 класса. Преобразование рациональных выражений. |
| Урок повторения и обобщения | Преобразование выражений. | Выполнять тождественные преобразования рациональных выражений. | Прил. №1. а) |
| П. №7-11г. |
|
|
| 2. |
| Повторение. Числовые функции. |
| Урок повторения и обобщения | Область определения функции, свойства функций. | Находить область определения функции, определять свойства функций и строить их графики. | Прил. №1. б) |
| П. №3-5г. |
|
|
| 3. |
| Повторение. Решение рациональных неравенств и их систем. |
| Урок повторения и обобщения | Линейные и квадратные неравенства и их системы. | Уметь решать линейные и квадратные неравенства и их системы. | Прил. №1. в) |
| П. №30-34г. |
|
|
| 4. |
| Входной срез. |
| Урок проверки знаний и умений |
|
| Прил. №1. г) |
|
|
|
|
|
| Действительные числа. |
| 10 |
|
|
|
|
|
|
|
|
| 5. |
| Натуральные и целые числа. Делимость натуральных чисел. |
| Урок систематизации знаний | Делимость целых чисел | Уметь применять свойства отношения делимости на множестве натуральных чисел. | Прил.№7 |
| 1.5-1.9г |
|
|
| 6. |
| Работа над ошибками. Признаки делимости. Простые и составные числа. |
| Урок систематизации знаний |
| Знать признаки делимости целых чисел, свойства простых чисел. | Прил.№7 |
| 1.34-1.39г 1.29 1.30г |
|
|
| 7. |
| Деление с остатком. НОД НОК нескольких натуральных чисел. |
| Урок систематизации знаний | Деление с остатком сравнения. | Знать и уметь применять свойства делимости. | Прил.№7 взаимоконтроль |
| 1.44-1.49г |
|
|
| 8. |
| Рациональные и иррациональные числа. |
| Урок систематизации знаний | Решение задач с целочисленными неизвестными. Понятие об иррациональном числе. Иррациональные числа. Десятичные приближения иррациональных чисел. | Уметь решать задачи с целочисленными неизвестными. Уметь доказывать иррациональность числа, находить иррациональные числа на отрезке. | Прил.№7 Самостоятельная работа 10'
|
| 2.2, 2.7, 2.10, 2.13, 2.16 |
|
|
| 9. |
| Действительные числа и числовая прямая. Числовые промежутки. |
| Урок систематизации знаний | Сравнения. Неравенство о среднем арифметическом двух чисел. | Зная свойства числовых неравенств уметь решать неравенства, определять промежутки знакопостоянства функции, решать уравнения с целой частью числа. | Прил. №7 |
| 4.3-4.4г 4.14-4.15г 4.25 ▪4.26г ▪4.27г |
|
|
| 10. |
| Модуль действительного числа. |
| Урок систематизации знаний | Модуль числа. | Зная свойства модуля, уметь решать уравнения и неравенства с модулем. | Прил.№7 Самостоятельная работа 10' |
| 5.1-5.11г 5.13-5.15г |
|
|
| 11. |
| Построение графиков функций, содержащих модуль. |
| Урок систематизации знаний. |
| Уметь строить графики функции, содержащие знак модуля. | Самостоятельная работа. |
| ▪5.25 5.22-5.24г
|
|
|
| 12. |
| Решение задач по теме «Действительные числа» |
| Урок обобщения знаний. |
|
|
|
| 5.27 |
|
|
| 13. |
| Контрольная работа №1 по теме «Действительные числа» |
| Урок проверки знаний и умений учащихся. |
|
| Контрольная работа |
|
|
|
|
| 14. |
| Метод математической индукции. |
| Урок ознакомления с новым материалом. | Метод математической индукции. | Иметь представление о методе математической индукции. |
| Метод математической индукции. | 6.2-6.6г 6.12-6.15г
|
|
|
|
| Глава 2. Числовые функции. |
|
9 |
|
|
|
|
|
|
|
|
| 15. |
| Работа над ошибками. Определение числовой функции и способы ее задания. |
| комбинированный | Числовая функция | Уметь строить кусочно-заданную функцию, функцию дробной части числа, функцию целой части числа | фронтальный |
| № 7.1г № 7.4 г №7.7
|
|
|
| 16. |
| Способы задания числовой функции. |
| проблемный | Способы задания функций | математический диктант |
| № 7.12-7.15г |
|
|
| 17. |
| Свойства функций. Область определения и область значения функции |
| поисковый | Область определения и множество значений функции | Уметь находить область определения и область значения функции | взаимообмен |
| №8.2-8.4г №8.9-8.12г |
|
|
| 18. |
| Монотонность и ограниченность функции. Четность функции |
| Комбинированный | Свойства функции: монотонность, четность и нечетность | Уметь использовать свойства функции при построении графика функций | математический диктант |
| № 8.18г 8.23-8.24г 8.27г
|
|
|
| 19. |
| Наибольшее и наименьшее значения функции |
| Урок изучения нового материала | Наибольшее и наименьшее значения функции | Уметь находить наибольшее и наименьшее значения функции | индивидуальная карточка |
| № 8.45в,г 8.46в,г Инд. № ▪8.47б
|
|
|
| 20. |
| Периодичность функции |
| урок | Периодичность, ограниченность функции | Уметь находить период функции, строить графики периодических функций | самостоятельная работа |
| №9.7г 9.8г |
|
|
| 21. |
| Обратная функция |
| Урок изучения нового материала | Нахождение функции обратной данной | Уметь находить обратную функцию | фронтальный |
| № 10.8г 10.9г |
|
|
| 22. |
| График обратной функции |
| комбинированный | График обратной функции | Уметь строить график обратной функции | взаимоконтроль |
| № 10.12в,г Инд. № ▪10.24г |
|
|
| 23. |
| Контрольная работа №2 по теме «Числовые функции» |
| Урок контроля знаний и умений |
|
| Контрольная работа |
|
|
|
|
|
| Тригонометрические функции |
| 21 |
|
|
|
|
|
|
|
|
| 24. |
| Работа над ошибками. Введение. Длина дуги окружности.
|
| Урок ознакомления с новым материалом. |
Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества. |
Понимать термины: числовая окружность, косинус, синус, тангенс и котангенс числового аргумента; радианная мера угла; уметь переводить градусную меру угла в радианную и наоборот; знать основные тригонометрические тождества и применять их при преобразовании тригонометрических выражений.
Вычислять значения функции по значению аргумента.
Уметь совершать преобразования тригонометрических выражений. |
|
| 11.1, 11.2(в,г) 11.3 |
|
|
| 25. |
| Числовая окружность |
| Комбинированный урок. |
|
| 11.06-11.10(в,г) |
|
|
| 26. |
|
Числовая окружность на координатной плоскости.
|
| Урок ознакомления с новым материалом. | Прил. №2.
|
| №12.1-12.4(в,г) Инд. 12.10 12.11 |
|
|
| 27. |
|
Координаты точек числовой окружности.
|
| Комбинированный урок. | Математический диктант 5′. Прил. №2 |
| 12.14-12.20(вг) Инд. 12.28-12.29г |
|
|
| 28. |
|
Синус и косинус
|
| Урок изучения нового материала. |
|
| 13.4-13.5 13.12-13.19(в,г) |
|
|
| 29. |
|
Тангенс и котангенс. |
| Урок изучения нового материала.
|
|
| 13.8-13.10(в,г) Инд.13.5г |
|
|
| 30. |
| Тригонометрические функции числового аргумента. |
| Комбинированный урок. | Самост. работа 10′ Прил. №2 |
| 14.1-14.5(в,г) 14.8-14.10(в,г) 14.14-14.16(в,г) |
|
|
| 31. |
| Основные тригонометрические тождества |
| Урок-практикум | Самост. работа |
| 14.11-14.13вг |
|
|
| 32. |
| Тригонометрические функции углового аргумента. |
| Комбинированный урок. | Самост. работа 10′ Прил. №2 |
| 15.1-15.4(в,г) 15.7-15.9(вг) ▪15.21-15.24 |
|
|
| 33. |
| Функция y = sin x, её свойства и график |
| Урок ознакомления с новым материалом, закрепление изученного. | Функции. Область определения и множество значений. | Уметь строить график функции y = sin x и y = соs x, описывать свойства функции. | Прил. №3 |
| 16.1-16.3г 16.8-16.13г 16.29-16.31г ▪16.66 |
21.09
21.09 |
|
| 34. |
| Функция y = соs x, её свойства и график. |
| Урок ознакомления с новым материалом, закрепление изученного. | Графики функций. Построение графиков. | Уметь строить график функции y = соs x, описывать свойства функции. | Прил.№3 |
| ▪16.60 ▪16.71 №16.72 16.33-16.34г |
|
|
| 35. |
| Контрольная работа №3 по теме «Определение тригонометрических функций». |
| Урок проверки знаний и умений учащихся. |
|
| Контрольная работа |
|
|
|
|
| 36. |
| Работа над ошибками. Построение графика функции y = mf (x). |
| Комбинированный урок |
Преобразования графиков функций. |
Выполнять преобразования графиков функций. | Прил.№3 |
| 17.1-17.9г ▪17.17-17.22 |
|
|
| 37. |
| Построение графиков тригонометрических функций |
| Урок-практикум | Растяжение и сжатие вдоль осей координат | Уметь строить график функции y=mf(x) | взаимоконтроль |
| 17.1-17.4вг |
|
|
| 38. |
| Построение графика функции y = f (kx) |
| Комбинированный урок |
|
| Прил.№3 |
| 18.1-18.6г 18.8-18.9 |
|
|
| 39. |
| Преобразование графиков тригонометрических функций. |
| Комбинированный урок | Самостоятельная работа 30′ |
| 18.15-18.16 ▪18.17 ▪18.18 |
|
|
| 40. |
| График гармонического колебания. |
| Комбинированный урок | Прил.№3 |
| 19.1-19.4б 19.12-19.13 |
|
|
| 41. |
| Функция y = tgx Свойства функции и её график. |
| Урок по технологической карте. | Область определения и множество значений. Графики функций. Построение гр-в. Свойства ф. | Уметь строить график функции y = tgx
| Самостоятельная работа 10′ Прил.№3 |
| 20.6-20.8г 20.2-20.5г 20.16г |
|
|
| 42. |
| Функция y = сtgx, Свойства функции и её график. |
| Урок по технологической карте. | Функция y = сtgx
| Уметь строить график функции y = сtgx и знать её свойства
| Самоконтроль |
| 20.19вг-20.23б 20.26б-▪20.27б |
|
|
| 43. |
| Функции y = arсsin x, y = arсcos x, их свойства и графики. |
| Урок ознакомления с новым материалом. |
Взаимно обратные функции. Область определения и область значения обратной функции. Нахождение функции, обратной данной. |
Уметь строить графики функций y = arсsin x, y = arсcos x, y = arсtg x, y = arсctg x, определять область определения и множество значений функций, обратных данным. | Прил.№3 |
| 21.1-21.5г 21.13-21.18г 21.19г ▪21.30 |
|
|
| 44. |
| Функции y = arсtg x, y = arсctg x, их свойства и графики. |
| Комбинированный урок. | Прил.№3 |
| 21.33-21.43г 21.46-21.48г ▪21.50-21.53г |
|
|
|
| Тригонометрические уравнения. |
| 9 |
|
|
|
|
|
|
|
|
| 45. |
| Контрольная работа за 1 полугодие «Тригонометрические функции». Простейшие тригонометрические уравнения и неравенства.
|
| Урок применения знаний и умений. | Простейшие тригонометрические уравнения и неравенства. | Уметь решать простейшие тригонометрические уравнения и неравенства. | Прил.№4 |
| 22.1-22.2(вг) 22.8-22.9 |
|
|
| 46. |
| Арккосинус и решение уравнения cos x = a |
| Урок ознакомления с новым материалом | Решение тригонометрических уравнений cos x = a | Уметь решать уравнения типа cos x = a | Прил.№4 |
| 22.3-22.5(вг) 22.23.б |
|
|
| 47. |
| Арксинус и решение уравнения sin x = a |
| Урок ознакомления с новым материалом | Решение тригонометрических уравнений sin x = a | Уметь решать уравнения типа sin x = a | Прил.№4 |
| 22.10-22.15г 22.23в |
|
|
| 48. |
| Арктангенс и решение уравнения tg x = a Арккотангенс и решение уравнения ctg x = a |
| Урок ознакомления с новым материалом | Решение тригонометрических уравнений tg x = a ctg x = a | Уметь решать уравнения типа tg x = a; и типа ctg x = a | Прил.№4 |
| 22.17-22.22г 22.26б |
|
|
| 49. |
| Решение простейших тригонометрических неравенств
|
| Урок ознакомления с новым материалом | Решение простейших тригонометрических неравенств
| Уметь решать неравенства типа sin x a, cos x a, tg x a, ctg xa | Прил.№4 |
| 22.42-22.43г 22.45-22.47г ▪22.48-22.49 |
|
|
| 50. |
| Решение тригонометрических уравнений, сводящихся к решению квадратного уравнения. |
| Комбинированный урок. | Тригонометрические уравнения. | Уметь решать тригонометрические уравнения, методом замены переменной и методом разложения на множители. | Прил.№4 |
| 23.1-23.6г |
|
|
| 51. |
| Решение однородных тригонометрических уравнений |
| Комбинированный урок. | Тригонометрические уравнения. | Уметь решать однородные тригонометрические уравнения первой и второй степени. | Прил.№4 |
| 23.11-23.15г |
|
|
| 52-53. |
| Контрольная работа №5 по теме «Тригонометрические уравнения» |
| Урок проверки знаний и умений учащихся. |
| Контрольная работа №3 или тест №2 |
|
|
|
|
|
|
| Преобразование тригонометрических выражений. |
| 18 |
|
|
|
|
|
|
|
|
| 54. |
| Работа над ошибками. Синус и косинус суммы аргументов. |
| Урок ознакомления с новым материалом. | Синус, косинус и тангенс суммы и разности двух углов. |
Уметь использовать тригонометрические формулы при преобразовании выражений. |
Прил.№5
|
| 24.3-24.6г 24.10-24.12г 24.15-24.18г |
|
|
| 55. |
| Синус и косинус разности аргументов. |
| Комбинированный урок. |
|
| 24.24-24.30г |
|
|
| 56. |
| Тангенс суммы и разности аргументов. |
| Комбинированный урок. |
| Математический диктант. Прил.№5 |
| 25.2-25.4г 25.5-25.7г |
|
|
| 57. |
| Решение тригонометрических уравнений и неравенств с применением формул тангенса суммы и разности аргументов.
|
| Урок - практикум. |
| Уметь решать уравнения, используя тригонометрические формулы синуса, косинуса и тангенса суммы и разности двух углов. | Прил.№5 |
| 25.17-25.20г ▪25.21-25.24 |
|
|
| 58. |
| Формулы приведения. |
| Урок ознакомления с новым материалом | Формулы приведения | Уметь применятьформулы приведения | математический диктант |
| 26.1-26.4г 26.8-26.10г |
|
|
| 59. |
| Решение тригонометрических уравнений с применением формул приведения. |
| Комбинированный урок | Простейшие тригонометрические уравнения | Уметь решать простейшие тригонометрические уравнения. | самостоятельная работа |
| 26.21-26.27г ▪26.33-26.37г |
|
|
| 60. |
| Формулы двойного аргумента. |
| Урок ознакомления с новым материалом. | Синус и косинус двойного угла. | Уметь использовать тригонометрические формулы двойного аргумента при преобразовании выражений. | Прил.№6 |
| 27.1-27.7г 27.9г 27.10г |
|
|
| 61. |
| Формула понижения степени. |
| Урок ознакомления с новым материалом. | Формулы половинного угла. | Уметь использовать тригонометрические формулы понижения степени при преобразовании выражений.
| Самостоятельная работа 10′ Прил.№6 |
| 27.54-27.56г |
|
|
| 62. |
| Преобразование суммы тригонометрических функций в произведение. |
| Урок ознакомления с новым материалом КСО. | Преобразование суммы тригонометрических функций в произведение. | Уметь преобразовывать тригонометрические выражения, используя формулу преобразования суммы тригонометрических функций в произведение.
| Самостоятельная работа 10′ Прил.№6 |
| 28.1-28.9г |
|
|
| 63. |
| Решение тригонометрических уравнений и неравенств с помощью преобразования сумм тригонометрических функций в произведение. |
| Урок-практикум КСО |
| Уметь решать тригонометрические уравнения с преобразованием сумм тригонометрических функций в произведение. | Прил.№6 Взаимообмен заданиями. |
| 28.26-28.32г ▪28.38 |
|
|
| 64. |
| Преобразование произведения тригонометрических функций в сумму |
| Урок ознакомления с новым материалом. | Преобразование тригонометрических функций в сумму. | Уметь преобразовывать тригонометрические выражения, используя формулу преобразования тригонометрических функций в сумму. | Прил.№6 |
| 29.1-29.6г |
|
|
| 65. |
| Решение тригонометрических уравнений с применением формул преобразования тригонометрических функций в сумму. |
| Урок-практикум |
| Уметь решать тригонометрические уравнения с применением формул преобразования тригонометрических функций в сумму. | Прил.№6 |
| 29.20-29.23г ▪29.26б
|
|
|
| 66. |
| Преобразование выражения Asin x + Bcos x к виду Csin (x+t) |
| Урок ознакомления с новым материалом. |
| Уметь преобразовывать тригонометрические выражения. | Прил.№6 | Преобразование выражения Asin x + Bcos x к виду Sin (x+t) | 30.1-30.7г 30.15-30.18г ▪30.21г |
|
|
| 67. |
| Методы решения тригонометрических уравнений. Решение уравнений с помощью подстановки. |
| Урок ознакомления с новым материалом КСО | Тригонометрические уравнения. | Уметь решать тригонометрические уравнения с помощью подстановки. | Прил.№6 |
| 31.1-31.6г ▪31.9 |
|
|
| 68. |
| Решение тригонометрич. уравнений, сведя его к однородному уравнению второй степени относительно половинного аргумента. |
| Комбинированный урок | Выражение тригонометрических функций через тангенс половинного аргумента. |
| Самостоятельная работа 10' Прил.№6 |
| 31.7-31.8г 31.12-31.15г ▪31.10 ▪31.16 |
|
|
| 69. |
| Решение задач по теме «Преобразование тригонометрических выражений» |
| Урок - соревнование |
|
|
|
| 31.39-31.43 |
|
|
| 70-71. |
| Контрольная работа №6 по теме «Преобразование тригонометрических выражений» |
| Урок контроля знаний и умений учащихся. |
|
| Контрольная работа или тест. |
|
|
|
|
|
| Производная |
| 24 |
|
|
|
|
|
|
|
|
| 72. |
| Работа над ошибками. Определение числовой последовательности и способы её задания |
| Комбинированный урок | Числовые последовательности. | Уметь определять последовательности, вычислять ее члены, строить графики последовательностей. | Прил.№9 взаимоконтроль. |
| 37.4-37.7г 37.16 37.41 37.42г |
|
|
| 73. |
| Определение предела последовательности. |
| Урок ознакомления с новым материалом. | Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Теоремы о пределах последовательностей. |
| Прил.№9 |
| 38.5 38.7 38.13-38.19г |
|
|
| 74. |
| Предел функции на бесконечности. Предел функции в точке. |
| Урок ознакомления с новым материалом. | Понятие о пределе функции в точке. Поведение функций на бесконечности. | Уметь вычислять пределы функций на бесконечности и в точке. | Взаимоконтроль Прил.№9 |
| 39.5-39.7г 39.11-39.17г |
|
|
| 75. |
| Определение производной. |
| Урок ознакомления с новым материалом. | Понятие о производной функции, физический и геометрический смысл производной.
| Уметь находить приращение функции. Знать физический и геометрический смысл производной. | Прил.№9 |
| 40.1-40.4г |
|
|
| 76. |
| Определение производной. |
| Урок ознакомления с новым материалом. | Понятие о производной функции, физический и геометрический смысл производной.
| Уметь находить приращение функции. Знать физический и геометрический смысл производной. | Прил.№9 |
| 40.13-40.16г
|
|
|
| 77. |
| Алгоритм нахождения производной. |
| Урок закрепления знаний и умений учащихся. |
| Уметь находить производную функции через приращение функции и приращение аргумента. | Прил.№9 |
| 41.1-41.10г |
|
|
| 78. |
| Формулы дифференцирования |
| Комбинированный урок | Производные основных элементарных функций. | Уметь вычислять производные элементарных функций. | Прил.№9 |
| 41.12-41.17г |
|
|
| 79. |
| Правила дифференцирования. |
| Комбинированный урок | Производные суммы, разности, произведения и частного. | Уметь вычислять производные, применяя правила и формулы дифференцирования. | Прил.№9 |
| 41.18-41.28г |
|
|
| 80. |
| Дифференцирование сложной функции. |
| Урок ознакомления с новым материалом. | Производная сложной функции. | Уметь вычислять производную сложной функции. | Прил.№9 |
| 42.1-42.7г
|
|
|
| 81. |
| Дифференцирование обратной функции |
| Комбинированный урок. | Производные обратных функций. | Уметь вычислять производные сложных функций. | Прил.№9 |
| 42.20-42.33г ▪42.38 |
|
|
| 82. |
| Уравнение касательной к графику функции. |
| Урок ознакомления с новым материалом. | Уравнение касательной к графику функции. | Уметь решать задачи с применением уравнения касательной к графику функции. | Самостоятельная работа 20′ Прил.№9 |
| 43.3-43.6г |
|
|
| 83. |
| Уравнение касательной к графику функции. |
| Урок ознакомления с новым материалом. | Уравнение касательной к графику функции. | Уметь решать задачи с применением уравнения касательной к графику функции. | Самостоятельная работа 20′ Прил.№9 |
| 43.22-43.28г |
|
|
| 84. |
| Решение задач по теме «Правила и формулы отыскания производных» |
| Урок обобщения и систематизации знаний. |
|
|
|
| 43.56-43.66г |
|
|
| 85-86. |
| Контрольная работа №7 по теме «Правила и формулы отыскания производных». |
| Урок контроля знаний и умений учащихся. |
|
| Контрольная работа 40′
|
|
|
|
|
| 87. |
| Работа над ошибками. Исследование функции на монотонность. |
| Урок изучения нового материала. | Применение производной к исследованию функций и построение графиков. | Исследовать функции и строить их графики с помощью производной. | Прил.№9 |
| 44.10-44.20г |
|
|
| 88. |
| Отыскание точек экстремума. |
| Урок изучения нового материала. |
|
| Прил.№9 |
| 44.63-44.68г |
|
|
| 88. 89 |
| Построение графиков функций. |
| Урок применения знаний и умений. | Асимптоты. | Уметь строить графики функций. | Прил.№9 |
| 45.1-45.7г ▪45.8-45.10б |
|
|
| 90. |
| Исследование функции и построение графика функции. |
| Урок применения знаний и умений уч-ся. |
|
| Прил.№9 Самост. работа 15′ |
|
|
|
|
| 91. |
| Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке. |
| Урок изучения нового материала. | Использование производной при нахождении наибольших и наименьших значений функции. | Уметь находить наибольшее и наименьшее значение функции, используя производную функцию. | Прил.№9 |
| 46.1-46.4г 46.10-46.15г |
|
|
| 92. |
| Задачи на отыскание наибольших и наименьших значений величин. |
| Комбинированный урок. | Использование производной при нахождении наибольших и наименьших значений. | Уметь решать задачи на отыскание наибольших и наименьших значений. | Прил.№9 Самостоятельная работа 10′ |
| 46.41-46.45б |
|
|
| 93. |
| Решение задач на нахождение наибольших и наименьших значений. |
| Урок обобщения и систематизации знаний |
|
|
|
| ▪46.53-46.56 |
|
|
| 94- 95. |
| Контрольная работа №8 по теме «Применение производной к исследованию функций» |
| Урок контроля знаний и умений учащихся. |
|
| Контрольная работа №9 |
|
|
|
|
|
| Комбинаторика и вероятность. |
| 3 |
|
|
|
|
|
|
|
|
| 96. |
| Работа над ошибками. Правило умножения. Комбинаторные задачи. Перестановка и факториалы.
|
| Урок систематизации знаний. | Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. |
Уметь решать простейшие комбинаторные задачи. | Прил. №10 |
| 47.1-47.8г 47.11-47.15г |
|
|
| 97.
|
| Выбор нескольких элементов. Формула Бинома-Ньютона. Биноминальные коэффициенты. Треугольник Паскаля. |
| Урок изучения нового материала.
| Формула Бинома-Ньютона Свойства биноминальных коэффициентов. Треугольник Паскаля. | Уметь вычислять коэффициенты бинома Ньютона по формуле. Уметь решать комбинаторные задачи с использованием треугольника Паскаля. | Прил.№10 Взаимоконтроль.
|
| 48.1-48.4г 48.10-48.13г
|
|
|
| 98. |
| Случайные события. |
| Урок изучения нового материала. | Элементарные и сложные события. | Уметь вычислять, в простейших случаях, вероятности событий на основе подсчета числа исходов. | Тест 10′ Прил.№10 |
| 49.1-49.6г
|
|
|
|
| Повторение |
| 7 |
|
|
|
|
|
|
|
|
| 99. |
| Решение тригонометрических уравнений методом введения новой переменной. |
| Урок обобщения и систематизации знаний учащихся. | Решение тригонометрических уравнений. |
|
|
| 22.38-22.40г |
|
|
| 100. |
| Решение однородных тригонометрических уравнений. |
| Урок обобщения и систематизации знаний учащихся. |
|
|
|
| ▪22.57б ▪22.58б ▪22.61г ▪22.62б |
|
|
| 101. |
| Решение тригонометрических уравнений с применением преобразования выражения. |
| Урок обобщения и систематизации знаний учащихся. | Решение тригонометрических уравнений. |
|
|
| ▪30.19-30.21г |
|
|
| 102. |
| Применение производной для исследования функции. |
| Урок обобщения и систематизации знаний учащихся. | Применение производной для исследования функции. |
|
|
| ▪44.71-44.76г |
|
|
| 103-104. |
| Итоговая контрольная работа №9. |
|
|
|
|
|
|
|
|
|
| 105. |
| Решение задач по всему курсу. |
| Урок обобщения и систематизации знаний учащихся. |
|
|
|
|
|
|
|
VII. Материально – техническое обеспечение
А. Г. Мордкович. Алгебра и начала анализа 10 класс. Учебник - М.: Мнемозина 2014 г.;
А. Г. Мордкович, Л. О. Денищева, Т. А. Корешкова, Т. Н. Мишустина, Е. Е. Тульчинская. Алгебра и начала анализа. 10 класс. Задачник – М: Мнемозина 2014 г.;
Александрова Л. А.под ред. А.Г.Мордковича. Алгебра и начала анализа 10 класс. Контрольные работы - М.: Мнемозина 2010 г.;
Л. А. Александрова. Алгебра и начала анализа 10 класс. Самостоятельные работы. М.: Мнемозина 2011 г.
А. Г. Мордкович. Алгебра и начала анализа 10 класс. Пособие для учителей М.: Мнемозина 2014 г.
29

 Получите свидетельство
Получите свидетельство Вход
Вход












 Рабочая программа и календарно-тематическое планирование по алгебре и началам математического анализа для учащихся 10 класса (базовый уровень) (0.27 MB)
Рабочая программа и календарно-тематическое планирование по алгебре и началам математического анализа для учащихся 10 класса (базовый уровень) (0.27 MB)
 0
0 1332
1332 69
69 Нравится
0
Нравится
0


