Практикум решения задач: «Зависимые события»

Федеральное Государственное Казенное Общеобразовательное Учреждение

«Кадетский корпус Следственного комитета Российской Федерации имени Александра Невского»

Теория вероятностей. Подготовка к ЕГЭ

Практикум решения задач: «Зависимые события»

Учитель математики Щедрина Римма Николаевна

г. Москва 2024

Задачи на проценты, вероятности зависимых событий, а также задачи, требующие последовательного подсчёта разных вероятностей

Диагностическая работа

1. На фабрике керамической посуды 5% произведенных кувшинов имеют дефект. При контроле качества выявляется 90% дефектных кувшинов. Остальные кувшины поступают в продажу. Найдите вероятность того, что случайно выбранный при покупке кувшин не имеет дефектов. Ответ округлите до тысячных.

Диагностическая работа

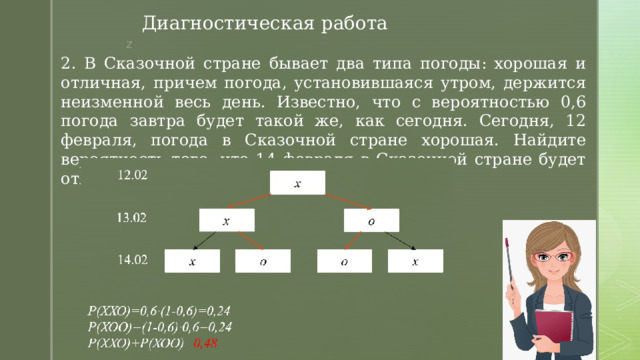
2. В Сказочной стране бывает два типа погоды: хорошая и отличная, причем погода, установившаяся утром, держится неизменной весь день. Известно, что с вероятностью 0,6 погода завтра будет такой же, как сегодня. Сегодня, 12 февраля, погода в Сказочной стране хорошая. Найдите вероятность того, что 14 февраля в Сказочной стране будет отличная погода.

Диагностическая работа

3. Чтобы поступить в ВУЗ на специальность «Туризм», абитуриент должен набрать на ЕГЭ не менее 55 баллов по каждому из трех предметов – математике, русскому языку и обществознанию. Чтобы поступить на специальность «Механизмы», нужно набрать не менее 55 баллов каждому из трех предметов – математике, русскому языку и физике. Вероятность того, что абитуриент А. получит не менее 55 баллов по математике, равна 0,5, по русскому языку – 0,7, по физике – 0,4, и по обществознанию – 0,6. Найдите вероятность того, что А. сможет поступить хотя бы на одну их упомянутых специальностей.

Диагностическая работа

4. На эстафете выступают команды – по одной от каждой из заявленных школ. Порядок выступления определяется жребием. Какова вероятность того, что команда из школы №12 будет выступать после команды из школы №15, но перед командой из школы №1? Результат округлите до сотых.

Теоретическая часть

Если имеются события А и В, то

Эти формулы следует применять, когда А и В–зависимые совместные события

Задачи о зависимых событиях

1. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Ответ: 0,52

Задачи на проценты

2. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Ответ: 0,75

3. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.

Ответ: 0,98

Разные задачи

4. На рок-фестивале выступают группы  — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.

Ответ: 0,33

5. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?

Ответ: 5

Разные задачи

6. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов  — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов  — математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку  — 0,8, по иностранному языку  — 0,7 и по обществознанию  — 0,5.Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.

Ответ: 0,408

Разные задачи

7. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.

Ответ: 0,392

Подготовка к контрольной работе

1. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,3, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,9?

2. В гончарной мастерской 20% произведённых чашек имеют дефект. При контроле качества продукции выявляется 85% дефектных чашек. Остальные чашки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке чашка не имеет дефектов. Ответ округлите до сотых.

3. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из России будет выступать после группы из Италии, но перед группой из фузии? Результат округлите до сотых.

4. Агрофирма закупает огурцы в двух теплицах. 70% огурцов из первой теплицы — огурцы высшей категории, а из второй теплицы — 80% огурцов высшей категории. Всего высшую категорию получает 72% огурцов. Найдите вероятность того, что огурец, купленный у этой агрофирмы, окажется из первой теплицы.

Домашнее задание

1. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,2, а при каждом последующем — 0,8. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,95?

2. На фабрике керамической посуды 20% произведённых пиал имеют дефект. При контроле качества продукции выявляется 90% дефектных пиал. Остальные пиалы поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке пиала не имеет дефектов. Ответ округлите до сотых.

3. Автофирма закупает колёса в двух магазинах. 10% колёс из первого магазина — колёса высшей категории, а из второго магазина — 2% колёс высшей категории. Всего высшую категорию получает 3% колёс. Найдите вероятность того, что колесо, купленное у этой автофирмы, окажется из первого магазина.

4. В Волшебной стране бывает два типа погоды: ясная и пасмурная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 7 августа, погода в Волшебной стране ясная. Найдите вероятность того, что 10 августа в Волшебной стране будет пасмурная погода.

Самостоятельная работа

Вариант 1

1. Чтобы поступить в институт на специальность «Автоматизация», абитуриент должен набрать на ЕГЭ не менее 60 баллов по каждому из трёх предметов — математике, русскому языку и физике. Чтобы поступить на специальность «Мехатроника», нужно набрать не менее 60 баллов по каждому из трёх предметов — математике, русскому языку и информатике. Вероятность того, что абитуриент У. получит не менее 60 баллов по математике, равна 0,4, по русскому языку — 0,5, по физике — 0,3 и по информатике — 0,2. Найдите вероятность того, что У. сможет поступить хотя бы на одну из двух упомянутых специальностей.

2. На спартакиаде выступают группы — по одной от каждой из заявленных городов. Порядок выступления определяется жребием. Какова вероятность того, что группа из г. Ростов будет выступать после группы из Казани и после группы из Уфы? Результат округлите до сотых.

3. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 60% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 30% яиц высшей категории. Всего высшую категорию получает 45% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

4. В торговом центре два одинаковых автомата продают шоколадки. Вероятность того, что к кожу дня в автомате закончится шоколад, равна 0,8. Вероятность того, что шоколад закончится в обоих автоматах, равна 0,62. Найдите вероятность того, что к конку дня шоколад останется в обоих автоматах .

Самостоятельная работа

Вариант 2

1. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 18% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 23% яиц высшей категории. Всего высшую категорию получает 22% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

2. Чтобы поступить в институт на специальность «Биотехника», абитуриент должен набрать на ЕГЭ не менее 80 баллов по каждому из трёх предметов — математике, русскому языку и химии. Чтобы поступить на специальность «Управление», нужно набрать не менее 80 баллов по каждому из трёх предметов — математике, русскому языку и обществознанию. Вероятность того, что абитуриент З. получит не менее 80 баллов по математике, равна 0,3, по русскому языку — 0,4, по химии — 0,7 и по обществознанию — 0,6. Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.

3. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из России будет выступать перед группой из Чехии и перед группой из Дании? Результат округлите до сотых.

4. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,7. Вероятность того, что кофе закончится в обоих автоматах, равна 0,56. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Интернет ресурсы

https://ya.ru/images/search?from=tabbar&img_url=https%3A%2F%2Fnaurok.com.ua%2Fuploads%2Ffiles%2F170115%2F308918%2F339664_html%2Fimages%2F308918%25203.png&lr=213&nomisspell=1&p=16&pos=16&rpt=simage&source=related-2&source-serpid=baPMI5eMksw3S6J-9L4p5A&text=картинка%20учительница%20на%20прозрачном%20фоне

https://ege.sdamgia.ru/problem?id=320206&ysclid=lvsebvnh9t647156815