Муниципальное общеобразовательное учреждение
«Пристенская основная общеобразовательная школа»
Валуйского района Белгородской области
| «Согласовано» Руководитель МО ____________Юрина Н.В. Протокол № 1 от
« 15 » июня 2012 г.
| «Согласовано» Заместитель директора школы по УВР _____________Грачёва Т.И.
«____»____________2012 г.
| «Утверждаю» Директор МОУ «Пристенская ООШ» _____________Даньшина Г.П. Приказ № ___ от «___»_________2012г.
|
РАБОЧАЯ ПРОГРАММА
Жировой Раисы
Игнатьевны
II квалификационная категория
по учебному предмету «Алгебра»
9 класс
Базовый уровень
2012 - 2013 учебный год
Пояснительная записка
Рабочая программа учебного курса алгебры для 9 класса составлена на основе:
Федерального компонента государственного образовательного стандарта, утверждённого Приказом Минобразования РФ от 05.03.2004 года № 1089
Программы общеобразовательных учреждений. Алгебра. 7-9 классы./ Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова. Москва. «Просвещение» 2010г.
Инструктивно-методического письма «О преподавании математики в 2012-2013учебном году в общеобразовательных учреждениях Белгородской области»
Место учебного предмета в решении общих целей и задач.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Реализация тематики данной программы направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
развитие таких качеств личности, как ясность и точность мысли, логическое мышление, пространственное воображение, алгоритмическая культура, интуиция, критичность и самокритичность;
формирование представление об идеях и методах математики как универсального языка науки и техники, средстве моделирования процессов и явлений;
воспитание средствами математики культуры личности, знакомство с жизнью и деятельностью видных отечественных и зарубежных учёных-математиков, понимание значимости математики для общественного прогресса.
Авторская программа используется в данной рабочей программе без изменений
Учебно-методический комплект
Программы общеобразовательных учреждений. Алгебра. 7-9 классы./ Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова. Москва. «Просвещение» 2010г.
Алгебра: учебник для 9 кл. /Ю.Н.Макарычев, Н.Г. Миндюк, К.И.Нешков, С.Б.Суворова/ под ред.
С.А.Теляковского.- М. Просвящение 2010г
Место учебного предмета в учебном плане
Программа рассчитана на 102 часа (3часа в неделю).
На I полугодие в неделю – 3 час, всего – 48ч.
На II полугодие в неделю – 3 час, всего – 54ч.
Из них:
Формы организации учебного процесса
Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, изучение свойств различных функций, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Урок-исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке. Любой учащийся может использовать компьютерную информационную базу по методам решения различных задач, по свойствам элементарных функций и т.д.
Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня обученности учащихся, тренировки технике тестирования. Тесты предлагаются как в печатном так и в компьютерном варианте. Причем в компьютерном варианте всегда с ограничением времени.
Урок-зачет. Устный опрос учащихся по заранее составленным вопросам, а также решение задач разного уровня по изученной теме.
Урок - самостоятельная работа. Предлагаются разные виды самостоятельных работ: двухуровневая – уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5»; большой список заданий разного уровня, из которого учащийся решает их по своему выбору. Рядом с учеником на таких уроках – включенный компьютер, который он использует по своему усмотрению.
Урок - контрольная работа. Проводится на двух уровнях:
уровень обязательной подготовки - «3», уровень возможной подготовки - «4» и «5».
Требования к уровню подготовленности учащихся.
В результате изучения математики ученик должен
знать/понимать
существо понятия математического доказательства; приводить примеры доказательств;
существо понятия алгоритма; приводить примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определённые функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
смысл идеализации, позволяющий решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
Свойства функций. Квадратичная функция
уметь:
- находить корни квадратного трёхчлена;
- выделять квадрат двучлена из квадратного трёхчлена ;
- раскладывать квадратный трёхчлен на множители;
- строить и читать график квадратичной функции, указывать координаты вершины параболы, её ось симметрии, направление ветвей;
- находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак;
- находить корни n-й степени;
- различать чётные и нечётные функции;
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
-представления о нахождении корня с помощью калькулятора.
Уравнения и неравенства с одной переменной
уметь:
-решать целые и дробные рациональные уравнения с одной переменной;
-решать неравенства вида ах2 + bx + c 0 или ах2 + bx + c
а # 0;
- решать уравнения третьей и четвёртой степени с помощью разложения на множители и введения вспомогательной переменной;
- решать несложные рациональные неравенства методом интервалов;
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
- обобщения и углубления сведений об уравнениях.
Уравнения и неравенства с двумя переменными
уметь:
- решать системы, в которых одно из уравнений первой степени, а другое второй способом подстановки, сводя решение таких систем к решению квадратного уравнения;
-решать простые системы, в которых оба уравнения второй степени;
-решать системы двух уравнений с двумя переменными графически, с помощью графиков, находить число решений данной системы;
- решать системы неравенств с двумя переменными;
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
- существенного расширения класса содержательных текстовых задач, решаемых с помощью систем уравнений;
- графической иллюстрации множеств решений некоторых простейших неравенств с двумя переменными и их систем.
Прогрессии
уметь:
- использовать индексное обозначение для изучения арифметической и геометрической прогрессий;
- работать с формулами n-го члена и суммы первых n членов прогрессий;
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
- возвращения к вычислениям, тождественным преобразованиям, решению уравнений, неравенств, систем;
- расширения круга предлагаемых задач.
Элементы комбинаторики и теории вероятностей
уметь:
-составлять те или иные комбинации элементов и подсчитывать их число;
- применять комбинаторное правило умножения, которое используется в дальнейшем для подсчёта числа перестановок, размещений и сочетаний;
- различать понятия «размещения» и «сочетания»;
- находить относительную частоту и вероятность случайного события;
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для: - статистического и классического подхода к определению вероятности случайных событий, в которых все исходы являются равновозможными.
Календарно-тематический план
| № урока | Содержание материала | № пункта, параграфа | Кол-во часов | Тип учебного занятия | Дата | Подго товка к ГИА |
|
| план | факт |
|
| Квадратичная функция. | Глава 1. | 22 |
|
|
|
|
| Функции и их свойства |
| 5 |
|
|
|
|
| 1/1 | Функция. Область определения и область значений функции. | п.1 | 1 | ИНМ |
|
| ВК |
| 2/2 | Функция. Область определения и область значений функции. | п. 2 | 1 | УЗ |
|
| П |
| 3/3 | Свойства функций. | п. 2 | 1 | ИНМ |
|
| П |
| 4/4 | Свойства функций. | п.2 | 1 | УКПЗ |
|
| Т№1 |
| 5/5 | Свойства функций. Входное контрольное тестирование | п. 2 | 1 | УКПЗ |
|
|
|
|
| Квадратный трёхчлен |
| 4 |
|
|
|
|
| 6/6 | Квадратный трёхчлен и его корни. | п. 3 | 1 | ИНМ |
|
| П |
| 7/7 | Квадратный трёхчлен и его корни. | п.3 | 1 | УЗ |
|
| П |
| 8/8 | Разложение квадратного трёхчлена на линейные множители. | п.4 | 1 | ИНМ |
|
| П |
| 9/9 | Разложение квадратного трёхчлена на линейные множители. | п.4 | 1 | УЗ |
|
| Т№2 |
| 10/10 | Контрольная работа №1 «Функции и их свойства» |
| 1 | КЗ |
|
|
|
|
| Квадратичная функция и ее график |
| 8 |
|
|
|
|
| 11/11 | Функция у=ах2, её график и свойства. | п.5 | 1 | ИНМ |
|
| П |
| 12/12 | Функция у=ах2, её график и свойства. | п.5 | 1 | УЗ |
|
| П |
| 13/13 | Графики функций у= ах2+n и у=а(х-m)2. | п.6 | 1 | ИНМ |
|
| П |
| 14/14 | Графики функций у= ах2+n и у=а(х-m)2. | п.6 | 1 | УЗ |
|
| П |
| 15/15 | Графики функций у= ах2+n и у=а(х-m)2. | п.6 | 1 | ОСМ |
|
| КТ |
| 16/16 | Построение графика квадратичной функции. | п.7 | 1 | ИНМ |
|
| П |
| 17/17 | Построение графика квадратичной функции. | п.7 | 1 | УЗ |
|
| П |
| 18/18 | Построение графика квадратичной функции. Тест. | п.7 | 1 | УКПЗ |
|
| КТ |
|
| Степенная функция. Корень n-й степени. |
| 3 |
|
|
|
|
| 19/19 | Функция у=хn. | п.8 | 1 | ИНМ |
|
| П |
| 20/20 | Корень n-ой степени. | п.9 | 1 | ИНМ |
|
| П |
| 21/21 | Корень n-ой степени. Тест. | п.9 | 1 | УКПЗ |
|
| КТ |
| 22/22 | Контрольная работа №2 «Функции и их свойства» |
| 1 | КЗ |
|
|
|
|
| Уравнения и неравенства с одной переменной. | Глава 2. | 14 |
|
|
|
|
| Уравнения с одной переменной |
| 8 |
|
|
|
|
| 23/1 | Целое уравнение и его корни. | п.12 | 1 | ИНМ |
|
| П |
| 24/2 | Целое уравнение и его корни. | п.12 | 1 | УЗ |
|
| П |
| 25/3 | Целое уравнение и его корни. | п.12 | 1 | УКПЗ |
|
| Т№5 |
| 26/4 | Дробные рациональные уравнения. | п.13 | 1 | ИНМ |
|
| П |
| 27/5 | Дробные рациональные уравнения. | п.13 | 1 | УЗ |
|
| П |
| 28/6 | Дробные рациональные уравнения. | п.13 | 1 | УЗ |
|
| П |
| 29/7 | Дробные рациональные уравнения. | п.13 | 1 | УКПЗ |
|
| П |
| 30/8 | Дробные рациональные уравнения. | п.13 | 1 | ОСМ |
|
| КТ |
|
| Неравенства с одной переменной |
| 5 |
|
|
|
|
| 31/9 | Решение неравенств второй степени с одной переменной. | п.14 | 1 | ИНМ |
|
| П |
| 32/10 | Решение неравенств второй степени с одной переменной. | п.14 | 1 | УЗ |
|
| П |
| 33/11 | Решение неравенств второй степени с одной переменной. | п.14 | 1 | УЗ |
|
| П |
| 34/12 | Решение неравенств методом интервалов. | п.15 | 1 | УКПЗ |
|
| П |
| 35/13 | Решение неравенств методом интервалов. Тест. | п.15 | 1 | ОСМ |
|
| КТ |
| 36/14 | Контрольная работа №3 «Уравнения и неравенства с одной переменной» |
| 1 | КЗ |
|
|
|
|
| Уравнения и неравенства с двумя переменными. | Глава 3. | 17 |
|
|
|
|
| Уравнения с двумя переменными и их системы |
| 12 |
|
|
|
|
| 37/1 | Уравнение с двумя переменными и его график. | п.17 | 1 | ИНМ |
|
| П |
| 38/2 | Уравнение с двумя переменными и его график. | п.17 | 1 | УЗ |
|
| П |
| 39/3 | Уравнение с двумя переменными и его график. | п.17 | 1 | УКПЗ |
|
| П |
| 40/4 | Графический способ решения систем уравнений. | п.18 | 1 | ИНМ |
|
| П |
| 41/5 | Графический способ решения систем уравнений. | п.18 | 1 | УЗ |
|
| П |
| 42/6 | Решение систем уравнений второй степени. | п.19 | 1 | ИНМ |
|
| П |
| 43/7 | Решение систем уравнений второй степени. | п.19 | 1 | УЗ |
|
| П |
| 44/8 | Решение систем уравнений второй степени. Самостоятельная работа. | п.19 | 1 | УКПЗ |
|
| П |
| 45/9 | Решение задач с помощью систем уравнений второй степени. | п.20 | 1 | ИНМ |
|
| П |
| 46/10 | Решение задач с помощью систем уравнений второй степени. | п.20 | 1 | УЗ |
|
| П |
| 47/11 | Решение задач с помощью систем уравнений второй степени. | п.20 | 1 | УКПЗ |
|
| П |
| 48/12 | Решение задач с помощью систем уравнений второй степени. Самостоятельная работа. | п.20 | 1 | ОС М |
|
| П |
|
| Неравенства с двумя переменными и их системы |
| 4 |
|
|
|
|
| 49/13 | Неравенства с двумя переменными. | п.21 | 1 | ИНМ |
|
| П |
| 50/14 | Неравенства с двумя переменными. | п.21 | 1 | УЗ |
|
| П |
| 51/15 | Системы неравенств с двумя переменными. | п.22 | 1 | УКПЗ |
|
| П |
| 52/16 | Системы неравенств с двумя переменными. | п.22 | 1 | ОСМ |
|
| П |
| 53/17 | Контрольная работа №4 «Уравнения и неравенства с двумя переменными» |
| 1 | КЗ |
|
|
|
|
| Арифметическая и геометрическая прогрессии. | Глава 4. | 15 |
|
|
|
|
| Арифметическая прогрессия |
| 7 |
|
|
|
|
| 54/1 | Последовательности. | п.24 | 1 | ИНМ |
|
| П |
| 55/2 | Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии. | п.25 | 1 | ИНМ |
|
| П |
| 56/3 | Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии. | п.25 | 1 | УЗ |
|
| П |
| 57/4 | Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии. Тест. | п.25 | 1 | УЗ |
|
| Т№9 |
| 58/5 | Формула суммы первых n членов арифметической прогрессии. | п.26 | 1 | ИНМ |
|
| П |
| 59/6 | Формула суммы первых n членов арифметической прогрессии. | п.26 | 1 | УЗ |
|
| П |
| 60/7 | Формула суммы первых n членов арифметической прогрессии. | п.26 | 1 | УКПЗ |
|
| П |
| 61/8 | Контрольная работа №5 «Арифметическая прогрессия» |
| 1 | КЗ |
|
|
|
|
| Геометрическая прогрессия |
| 6 |
|
|
|
|
| 62/9 | Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии. | п.27 | 1 | ИНМ |
|
| П |
| 63/10 | Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии. | п.27 | 1 | УЗ |
|
| П |
| 64/11 | Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии. Тест. | п.27 | 1 | УЗ |
|
| КТ |
| 65/12 | Формула суммы первых n членов геометрической прогрессии. | п.28 | 1 | ИНМ |
|
| Т№11 |
| 66/13 | Формула суммы первых n членов геометрической прогрессии. | п.28 | 1 | УЗ |
|
| П |
| 67/14 | Формула суммы первых n членов геометрической прогрессии. | п.28 | 1 | УКПЗ |
|
| П |
| 68/15 | Контрольная работа №5 «Геометрическая прогрессия» |
| 1 | КЗ |
|
|
|
|
| Элементы комбинаторики и теории вероятностей. | Глава 5 | 13 |
|
|
|
|
| Элементы комбинаторики |
| 9 |
|
|
|
|
| 69/1 | Примеры комбинаторных задач. | п.30 | 1 | ИНМ |
|
| П |
| 70/2 | Примеры комбинаторных задач. | п.30 | 1 | УЗ |
|
| П |
| 71/3 | Перестановки. | п.31 | 1 | ИНМ |
|
| П |
| 72/4 | Перестановки. | п.31 | 1 | УЗ |
|
| П |
| 73/5 | Размещения. | п.32 | 1 | ИНМ |
|
| П |
| 74/6 | Размещения. | п.32 | 1 | УЗ |
|
| П |
| 75/7 | Сочетания. | п.33 | 1 | ИНМ |
|
| П |
| 76/8 | Сочетания. | п.33 | 1 | УЗ |
|
| П |
| 77/9 | Сочетания. Самостоятельная работа. | п.33 | 1 | УКПЗ |
|
| П |
|
| Начальные сведения из теории вероятностей |
| 3 |
|
|
|
|
| 78/10 | Относительная частота случайного события. | п.34 | 1 | ИНМ |
|
| П |
| 79/11 | Вероятность равновозможных событий. | п.35 | 1 | ИНМ |
|
| П |
| 80/12 | Сложение и умножение вероятностей. | п.36 | 1 | УКПЗ |
|
| П |
| 81/13 | Контрольная работа №7 «Элементы комбинаторики и теории вероятностей» |
| 1 | КЗ |
|
|
|
|
| Повторение. |
| 21 |
|
|
|
| 82/1 | Вычисления. |
| 1 | ПМ |
|
| П |
| 83/2 | Вычисления. |
| 1 | ПМ |
|
| П |
| 84/3 | Вычисления. |
| 1 | ПМ |
|
| КТ |
| 85/4 | Тождественные преобразования. |
| 1 | ПМ |
|
| П |
| 86/5 | Тождественные преобразования. |
| 1 | ПМ |
|
| П |
| 87/6 | Тождественные преобразования. |
| 1 | ПМ |
|
| П |
| 88/7 | Тождественные преобразования. |
| 1 | ПМ |
|
| Т№21 |
| 89/8 | Уравнения и системы уравнений. |
| 1 | ПМ |
|
| П |
| 90/9 | Уравнения и системы уравнений. |
| 1 | ПМ |
|
| П |
| 91/10 | Уравнения и системы уравнений. |
| 1 | ПМ |
|
| П |
| 92/11 | Уравнения и системы уравнений. |
| 1 | ПМ |
|
| П |
| 93/12 | Уравнения и системы уравнений. |
| 1 | ПМ |
|
| КТ |
| 94/13 | Неравенства. Системы неравенств. |
| 1 | ПМ |
|
| П |
| 95/14 | Неравенства. Системы неравенств. |
| 1 | ПМ |
|
| П |
| 96/15 | Неравенства. Системы неравенств. |
| 1 | ПМ |
|
| П |
| 97/16 | Неравенства. Системы неравенств. |
| 1 | ПМ |
|
| КТ |
| 98/17 | Функции. |
| 1 | ПМ |
|
| П |
| 99/18 | Функции. |
| 1 | ПМ |
|
| П |
| 100/19 | Функции. |
| 1 | ПМ |
|
| П |
| 101/20 | Итоговая контрольная работа. |
| 1 | ПМ |
|
| КТ |
| 102/21 | Итоговая контрольная работа. |
| 1 | КЗ |
|
|
|
Условные обозначения
ИНМ – изучение нового материала
ЗНЗ – закрепление новых знаний
УКПЗ – урок комплексного применения знаний
КЗ – контроль знаний
ОУ – обобщающий урок
КТ – контрольный тест
КУ – комбинированный урок
Содержание учебного предмета
Глава 1. Свойства функций. Квадратичная функция (22 часа)
Функция. Свойства функций. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Функция у = ах2 + bх + с, её свойства и график. Неравенства второй степени с одной переменной. Метод интервалов.
Цель: расширить сведения о свойствах функций, ознакомить обучающихся со свойствами и графиком квадратичной функции, сформировать умение решать неравенства вида ах2 + bх + с0 ах2 + bх + с0.
В начале темы систематизируются сведения о функциях. Повторяются основные понятия: функция, аргумент, область определения функции, график. Даются понятия о возрастании и убывании функции, промежутках знакопостоянства. Тем самым создается база для усвоения свойств квадратичной и степенной функций, а также для дальнейшего углубления функциональных представлений при изучении курса алгебры и начал анализа.
Подготовительным шагом к изучению свойств квадратичной функции является также рассмотрение вопроса о квадратном трехчлене и его корнях, выделении квадрата двучлена из квадратного трехчлена, разложении квадратного трехчлена на множители.
Изучение квадратичной функции начинается с рассмотрения функции у=ах2, её свойств и особенностей графика, а также других частных видов квадратичной функции – функции у=ах2+n, у=а(х-m)2. Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы обучающиеся поняли, что график функции у = ах2 + bх + с может быть получен из графика функции у = ах2 с помощью двух параллельных переносов. Приёмы построения графика функции у = ах2 + bх + с отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у обучающихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы.
При изучении этой темы дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак.
Формирование умений решать неравенства вида ах2 + bх + с0 ах2 + bх + с0, осуществляется с опорой на сведения о графике квадратичной функции (направление ветвей параболы ее расположение относительно оси Ох).
Обучающиеся знакомятся с методом интервалов, с помощью которого решаются несложные рациональные неравенства.
Обучающиеся знакомятся со свойствами степенной функции у=хn при четном и нечетном натуральном показателе n.. Вводится понятие корня n-й степени. Обучающиеся должны понимать смысл записей вида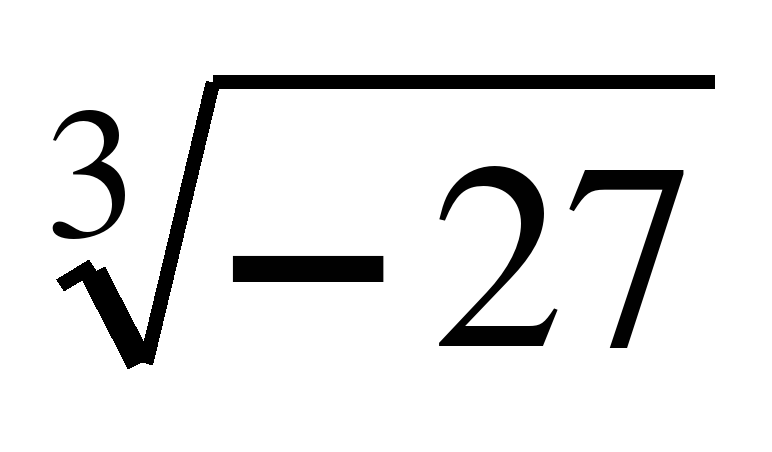 
, 
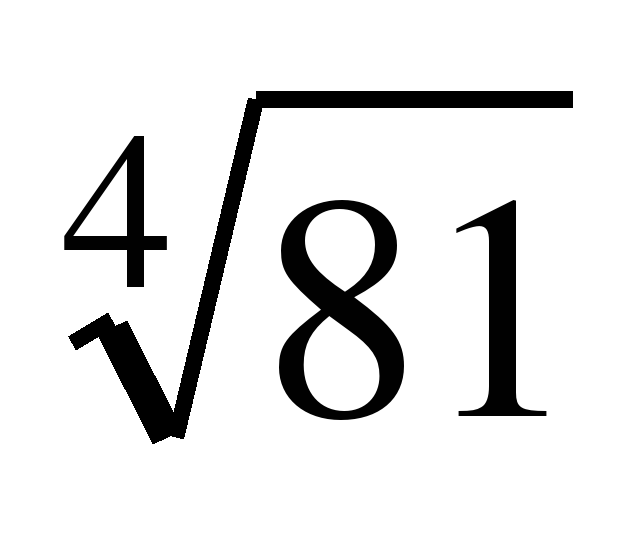. Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.
Глава 2 и 3. Уравнения и неравенства с одной переменной (14часов). Уравнения и неравенства с 2 переменными (17 часов)
Целые уравнения. Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение задач с помощью систем уравнений второй степени.
Цель: систематизировать и обобщить сведения о решении целых с одной переменной, Выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем; выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем.
В этой теме завершается изучение рациональных уравнений с одной переменной. В связи с этим проводится некоторое обобщение и углубление сведений об уравнениях. Вводятся понятия целого рационального уравнения и его степени. Обучающиеся знакомятся с решением уравнений третьей степени и четвертой степени с помощью разложения на множители и введения вспомогательной переменной. Метод решения уравнений путем введения вспомогательных переменных будет широко использоваться дальнейшем при решении тригонометрических, логарифмических и других видов уравнений.
В данной теме завершаемся изучение систем уравнений с двумя. переменными. Основное внимание уделяется системам, в которых одно из уравнений первой степени, а другое второй. Известный обучающимся способ подстановки находит здесь дальнейшее применение и позволяет сводить решение таких систем к решению квадратного уравнения.
Ознакомление обучающихся с примерами систем уравнений с двумя переменными, в которых оба уравнения второй степени, должно осуществляться с достаточной осторожностью и ограничиваться простейшими примерами.
Привлечение известных обучающимся графиков позволяет привести примеры графического решения систем уравнений. С помощью графических представлений можно наглядно показать обучающимся, что системы двух уравнений с двумя переменными второй степени могут иметь одно, два, три, четыре решения или не иметь решений.
Разработанный математический аппарат позволяет существенно расширить класс содержательных текстовых задач, решаемых с помощью систем уравнений.
Глава 4. Арифметическая и геометрическая прогрессии (15 часов)
Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы первых n членов прогрессии. Бесконечно убывающая геометрическая прогрессия.
Цель: дать понятия об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.
При изучении темы вводится понятие последовательности, разъясняется смысл термина «n-й член последовательности», вырабатывается умение использовать индексное обозначение. Эти сведения носят вспомогательный характер и используются для изучения арифметической и геометрической прогрессий.
Работа с формулами n-го члена и суммы первых n членов прогрессий, помимо своего основного назначения, позволяет неоднократно возвращаться к вычислениям, тождественным преобразованиям, решению уравнений, неравенств, систем.
Рассматриваются характеристические свойства арифметической и геометрической прогрессий, что позволяет расширить круг предлагаемых задач.
Глава 5. Элементы комбинаторики и теории вероятностей (13 часов)
Комбинаторное правило умножения. Перестановки, размещения, сочетания. Относительная частота и вероятность случайного события.
Цель: ознакомить обучающихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчета их числа; ввести понятия относительной частоты и вероятности случайного события.
Изучение темы начинается с решения задач, в которых требуется составить те или иные комбинации элементов и. подсчитать их число. Разъясняется комбинаторное правило умножения, которое исполнятся в дальнейшем при выводе формул для подсчёта числа перестановок, размещений и сочетаний. При изучении данного материала необходимо обратить внимание обучающихся на различие понятий «размещение» и «сочетание», сформировать у них умение определять, о каком виде комбинаций идет речь в задаче.
В данной теме обучающиеся знакомятся с начальными сведениями из теории вероятностей. Вводятся понятия «случайное событие», «относительная частота», «вероятность случайного события». Рассматриваются статистический и классический подходы к определению вероятности случайного события. Важно обратить внимание обучающихся на то, что классическое определение вероятности можно применять только к таким моделям реальных событий, в которых все исходы являются равновозможными.
Повторение(21 час)
Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры основной общеобразовательной школы.
Формы и средства контроля
1. Оценка письменных контрольных работ обучающихся по математике. Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
Отметка «2» ставится, если:
2. Оценка устных ответов обучающихся по математике Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Перечень учебно-методических средств обучения
Литература (основная и дополнительная)
1.Алгебра: учеб. для 9 кл. / Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова; под ред. С.А.Теляковского. – М.: Просвещение, 2008
2.Макарычев Ю.Н. Алгебра: элементы статистики и теории вероятностей: учеб. пособие для 7-9 кл. / / Ю.Н.Макарычев, Н.Г.Миндюк. М.: Просвещение, 2008
3.Ю.Н.Макарычев. Алгебра: дидактические материалы для 9 класса Ю.Н.Макарычев, Н.Г.Миндюк, Л.М.Короткова. - М.: Просвещение, 2008
5.Макарычев Ю.Н. Изучение алгебры в 7-9 классах /Ю.Н.Макарычев, Н.Г.Миндюк, С.Б.Суворова. - М.: Просвещение, 2008
6.Рабочая тетрадь по алгебре для 9 класса / Ю.М.Колягин, Ю.В.Сидоров, Ткачёва М.В. и др. - М.: Просвещение, 2008
7.Алгебра: сб. заданий для подготовки к итоговой аттестации в 9 кл. / Л.В.Кузнецова, С.Б.Суворова, Е.А.Бунимович и др. - М.: Просвещение, 2008
8.Алгебра-9. Поурочные планы. Л.А.Тапилина, Т.Л.Афанасьева. Волгоград. «Учитель». 2002
9.Обязательный минимум содержания основного общего образования по математике
10.Федеральный компонент государственного стандарта общего образования. Математика. Основное общее образование
11.Оценка качества подготовки выпускников основной школы по математике/ Г.В.Дорофеев и др. – М.: Дрофа, 2000
12.Журнал «Математика в школе» №1 – 2006г.
13.Алгебра 9 класс. Пособие для самостоятельной подготовки к итоговой аттестации 2006. Ф.Ф.Лысенко, Ростов-на-Дону, «Легион». 2005
14.Учебно-методическая газета «Математика», приложение «1 сентября» №9 – 2006г, стр. 7
15.Миндюк М.Б., Миндюк Н.Г. Тематический контроль. Алгебра 9 класс. – М. Интеллект-Центр. 2007
16.Крайнева Л.Б. и др. Сборники тестовых заданий для тематического и обобщающего контроля. Алгебра 9 класс. – М. Интеллект-Центр. 2007
17.Беленкова Е.Ю. Лебединцева Е.А. Задания для обучения и развития учащихся. Алгебра. 9 класс. М. Интеллект-Центр. 2007
18. Задания для подготовки к письменному экзамену по математике в 9 классе/ Л.И.Звавич, Д.И.Аверьянов – М.: Просвещение. 2005
19.Государственная итоговая аттестация выпускников 9 классов в новой форме. Алгебра. 2009/ ФИПИ. Е.А.Бунимович, Т.В.Колесникова, Л.В.Кузнецова. М. Интеллект-Центр. 2009
20.ГИА-2010. Экзамен в новой форме. Алгебра. 9 класс. Л.В.Кузнецова, С.Б.Суворова и др. М.: Астрель, 2009
Получите свидетельство
Вход
Рабочая программа по алгебре (9 класс) (0.27 MB)
0
836
89
Нравится
0
