Урок обобщение и систематизация знаний, умений и навыков учащихся

«Угол между прямыми в пространстве, прямой и плоскостью.

Координатный метод».

Учитель высшей категории МБОУ «СОШ №5» Быстрова Нина Николаевна

Урок по теме: «Угол между прямыми в пространстве, прямой и плоскостью. Координатный метод».

Тип урока. Урок обобщение и систематизация знаний, умений и навыков учащихся.

Цель урока:

• повторить определение угла между прямыми в пространстве, угла между прямой и плоскостью;

• повторить изученный ранее материал, необходимый при решении задач;

• рассмотреть решение задач уровня №14;

• вырабатывать навыки и умения решения задач на нахождение угла между прямыми в пространстве, угла между прямой и плоскостью, применяя метод координат.

Оборудование: компьютер, проектор, экран

Содержание урока:

1. Организационный момент. 2 мин.

2. Повторение   теоретического материала. Фронтальная работа с классом по основным понятиям темы. 5 мин.

3. Обобщение и систематизация изученного. Решение двух задач. 20 мин.

4. Фронтальная работа с классом по основным понятиям темы.4 мин

5. Обобщение и систематизация изученного. Решение одной задачи разными методами. 10 мин.

6. Рефлексия. 1 мин

7. Итог урока. 1мин

8. Этап информации о домашнем задании. 2 мин

Ход урока

1. Организационный момент.

Задание №14 Единого государственного экзамена представляет собой стереометрическую задачу на определение расстояний или углов в пространстве между объектами, связанными с некоторыми многогранниками. (Слайд 1,2)

Сегодня на уроке мы повторим понятие  угла между прямыми, угла между прямой и плоскостью.   Цель нашего урока – приобрести  опыт решения задач на нахождении угла между прямыми в пространстве, угла между прямой и плоскостью.   Мы увидим, как отражается данная тема в вариантах ЕГЭ.

1. Повторение теоретического материала. Решение задач.

1. Фронтальная работа с классом по основным понятиям темы. Повторение теории с помощью презентации «Задания №14 на ЕГЭ. Координатный метод. Углы в пространстве».

Координатный метод позволяет найти угол между прямыми в пространстве, используя их направляющие векторы. Для нахождения угла между двумя прямыми необходимо найти косинус угла между их направляющими векторами по формуле 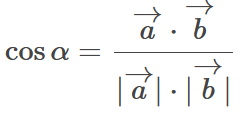. (слайд 3) Рассмотрим решение таких задач координатным методом. Обобщение и систематизация изученного. Решение двух задач с помощью презентации (исследовательская работа учащихся).

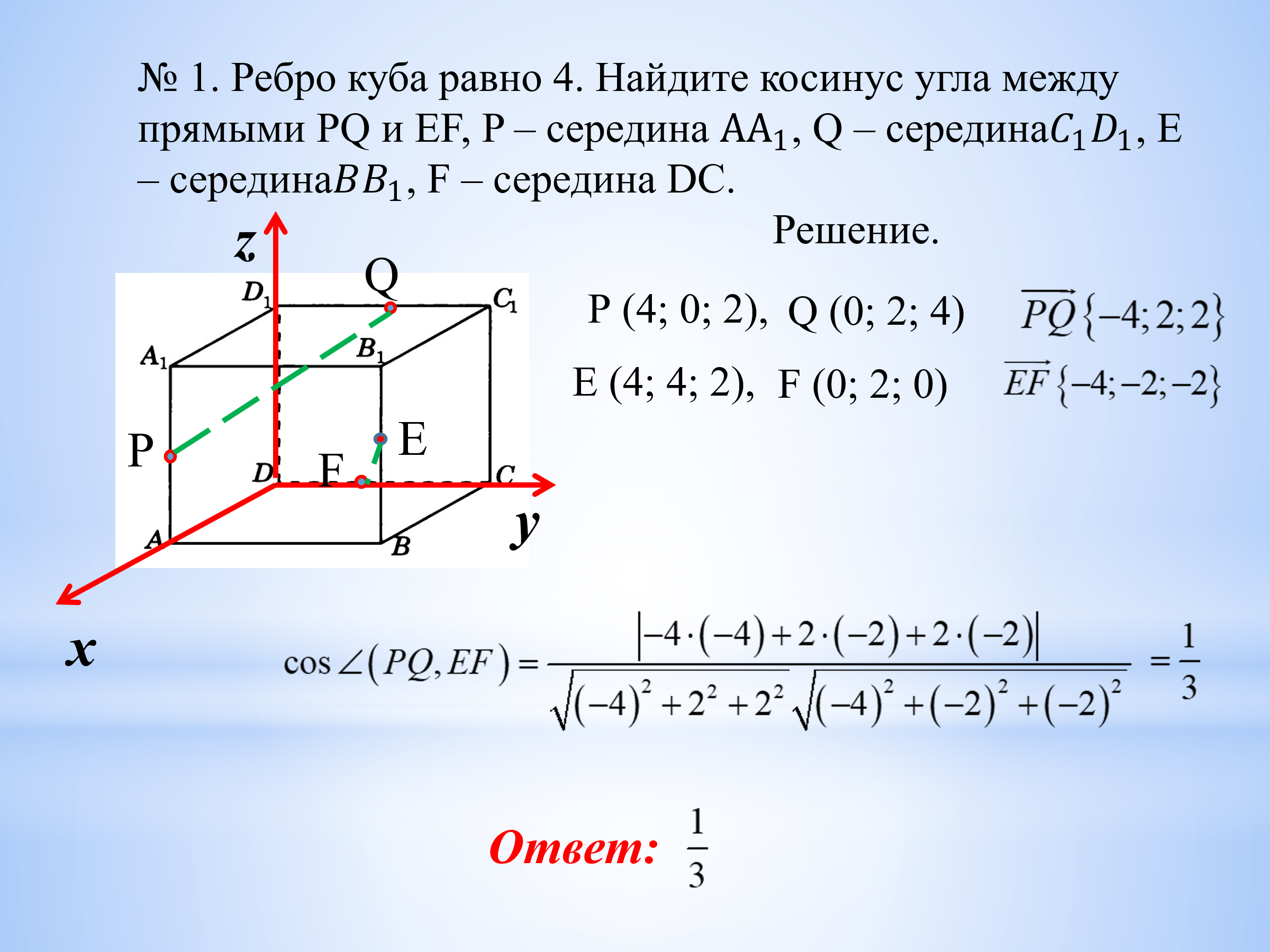
Задача 1. Ребро куба равно 4. Найдите косинус угла между прямыми PQ и EF, P – середина 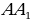, Q – середина 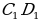, Е – середина 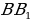, F – середина DC. (слайд 4)

Задача 2. В правильной шестиугольной призме все ребра равны 1. Найдите косинус угла между прямым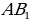и и 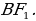(слайд 5).

Самостоятельная работа

Задача 3. В правильной треугольной призме все ребра равны 1. Найдите угол между прямыми 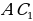и .

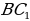1. Фронтальная работа с классом по основным понятиям темы. Повторение теории с помощью презентации «Угол между прямой и плоскостью». (слайд 10,11).

Условия задач, в которых приходится отыскивать угол между прямой и плоскостью, разнообразны. Часто справиться с задачей нахождения угла между прямой и плоскостью  помогают признаки равенства или подобия фигур, теорема косинусов, определения синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника. Сегодня мы при решение такой задачи воспользуемся методом координат.

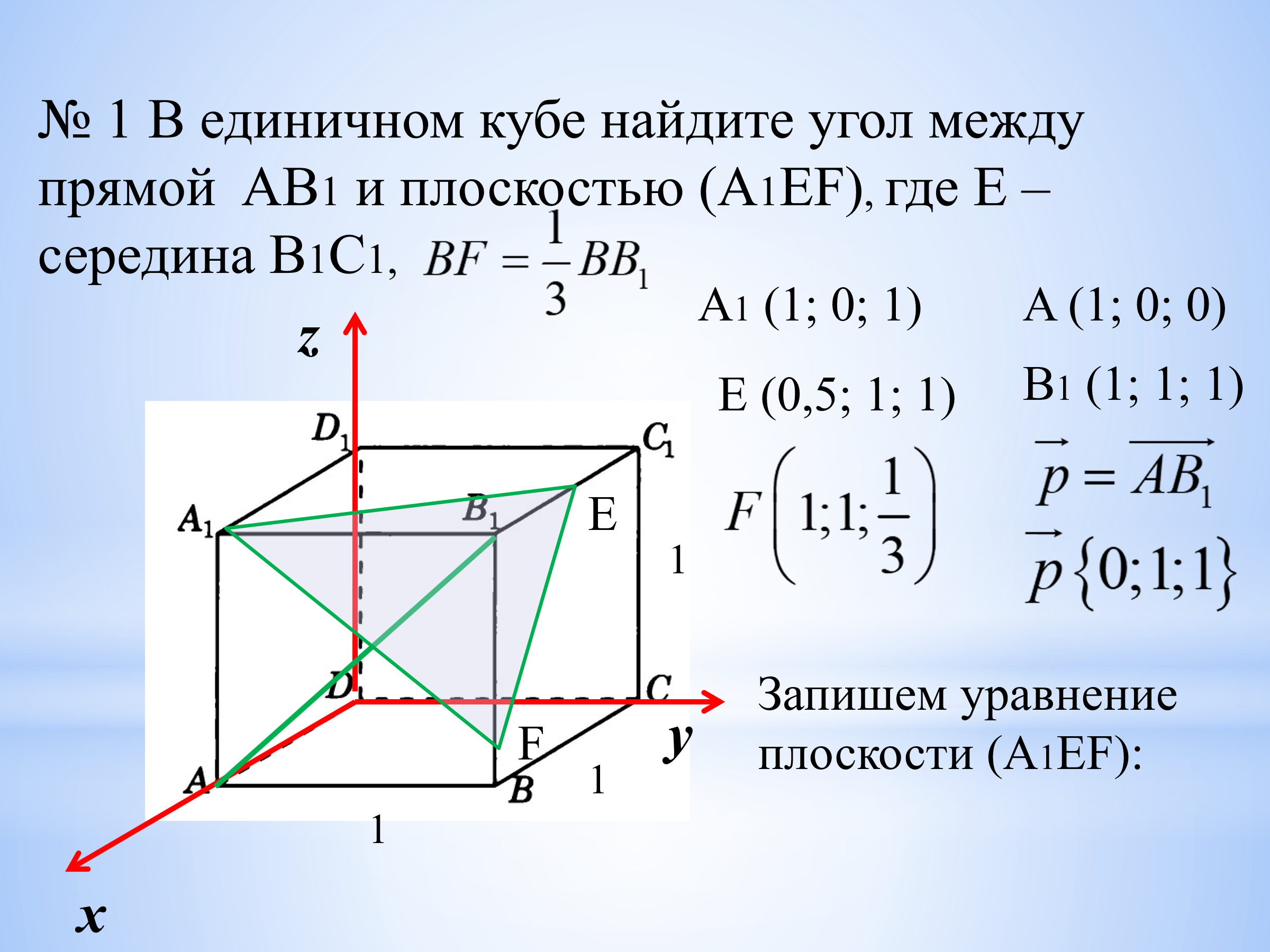
Задача4. В единичном кубе найдите угол между прямой AВ1 и плоскостью (А1EF), где Е – середина В1С1, BF = 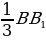. (слайд 12-14).

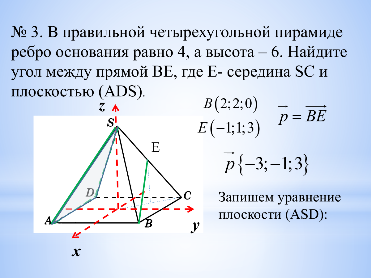
Задача 5. В правильной четырехугольной пирамиде ребро основания равно 4, а высота – 6. Найдите угол между прямой ВЕ, где Е- середина SC и плоскостью (АDS). (слайд 18-20).

Самостоятельная работа

Задача 6. В правильной шестиугольной призме все ребра равны 1. Найдите синус угла между прямой AВ1 и плоскостью (АСF1).

1. Рефлексия. Справились ли мы с поставленными задачами на урок? Чувствуете ли вы себя увереннее, готовым к сдаче ЕГЭ по теме «Угол между прямыми в пространстве, прямой и плоскостью».? Может быть, для кого-то из вас остались нерешенные проблемы, над которыми еще стоит поработать самостоятельно?

2. Комментарий домашнего задания и подведения итогов

На этом уроке мы:

• Работали с такими понятиями, как угол между прямыми в пространстве, угол между прямой и плоскостью;

• Решили задачи, где наглядно продемонстрировали использование  определения угла между прямыми в пространстве, угла между прямой и плоскостью;

•     Рассмотрели геометрический метод решения задач и координатно – векторный метод. Координатно – векторный метод позволяет избежать трудностей в построении и вычислении углов и расстояний между объектами в пространстве. От выпускников требуется знание нескольких формул и навыки в решении простейших задач, основная нагрузка при решении задач приходится на вычислительную часть.