Цели и задачи урока:(слайд 2)
Обучающие:
повторить теоретический материал;
обобщить и систематизировать знания для нахождения первообразных;
отработать навыки вычисления интегралов и площадей криволинейных трапеций.
Развивающие:
развить навыки самостоятельного мышления;
развить интеллектуальные навыки, внимание, память;
развить информационную и коммуникативную культуру обучающихся.
Воспитательные:
воспитывать математическую культуру обучающихся;
повысить интерес к изучаемому материалу;
Оборудование: Экран и мультимедийный проектор, карточки для индивидуальной работы, тесты для каждого обучающегося.
Тип урока: урок обобщения ( систематизации знаний, умений, навыков).
Формы: работа в парах, фронтальная, индивидуальная.
Ход урока:
- Организационный момент.
- Мотивационное начало урока
Преподаватель: Здравствуйте, тема нашего сегодняшнего урока: Вычисление площади криволинейной трапеции с помощью определенного интеграла. Цель нашего урока – повторить какая фигура называется криволинейной трапецией, как находится площадь криволинейной трапеции, выполнить задания из учебника и решить тестовое задание на оценку.
Проверка домашнего задания. Программированный контроль.
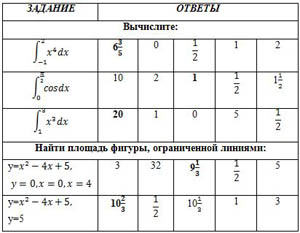
На столах у каждого учащегося лежит данная работа, которая дает возможность проверить выполнение домашней работы. Правильный ответ обводят и сдают на проверку.
Работа по повторению ранее изученного материала
Вопросы по теме «Первообразная и интеграл» (слайд №3, 4, 5, 6)
Дайте определение первообразной.
Сформулируйте три правила нахождения первообразных.
Какую фигуру называют криволинейной трапецией?
Запишите формулу Ньютона - Лейбница.
- Алгоритм нахождения площадикриволинейной трапеции: (слайд №7)
Изобразить чертеж и убедится, является ли данная фигура криволинейной трапецией
Найти первообразную F(x)
Применить формулу Ньютона –Лейбница S=F(b) - F(a)
Из истории. Группа учащихся выступают сообщениями о происхождении терминов и обозначений по теме «Первообразная. Интеграл», из истории интегрального исчисления, о математиках, сделавших открытия по данной теме.
Интеграл, интегрирование, интеграция… Однокоренные слова, к тому же вышедшие за пределы математики и ставшие почти обиходными. В газетах читаем об интеграции наук, культур, в политике и экономике ведут речь об интегральных процессах. Любопытно, что идеи интегрального исчисления возникли задолго до появления идей дифференциального исчисления. Греческие математики Эвдокс и Архимед (4;3 века до нашей эры) для решения задач вычисления площадей и объемов придумали разбивать фигуру на бесконечно большое число бесконечно малых частей и искомую площадь (или объем) вычисляли как сумму площадей (или объемов) полученных элементарных кусочков. Кеплер, Галилей, Кавальери, Паскаль, Ферма…
Во второй половине 17 века идеи, подготовленные всем предшествующим развитием математики были гениально осознаны, обобщены и приведены в систему английским физиком и математиком И. Ньютоном и немецким математиком В. - Г. Лейбницем. Они создали стройную систему понятий и выработали правила, по которым можно вычислять.
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход



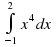
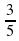
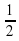
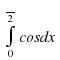
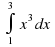
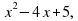
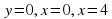
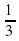
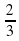
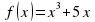
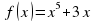
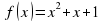
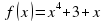
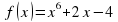
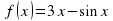
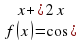
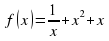
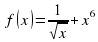









 Урок математики "Вычисление площади криволинейной трапеции с помощью определенного интеграла" (97.2 КB)
Урок математики "Вычисление площади криволинейной трапеции с помощью определенного интеграла" (97.2 КB)
 0
0 2023
2023 448
448 Нравится
0
Нравится
0





