Содержание программы
Титульный лист 1
Пояснительная записка 3-4
Содержание учебного предмета 5-6
Требования к уровню подготовки обучающихся 7-8
Календарно-тематический план 9-11
Учебно-методическое планирование 12
Список литературы 13
Пояснительная записка
Рабочая программа по математике разработана на основе:
- Закона РФ «Об образовании»;
- приказа комитета образования и науки Курской области от 23 марта 2007 года № 1-421 «Об утверждении регионального базисного учебного плана для общеобразовательных учреждений Курской области, реализующих программы общего образования»;
- приказа комитета образования и науки Курской области от17.08.2012года № 1-893 «О внесении изменений и дополнений в региональный базисный учебный план для общеобразовательных учреждений Курской области, реализующих программы общего образования, утвержденный приказом комитета образования и науки Курской области от 23.03.2007 г. № 1-421 «Об утверждении регионального базисного учебного плана для общеобразовательных учреждений Курской области, реализующих программы общего образования» с изменениями, внесенными приказами комитета образования и науки Курской области от 09.12.2011 г. № 1-1234 и от23.03.2012 г. № 1-285);
- федерального компонента государственного стандарта среднего (полного) общего образования, утвержденного Приказом Минобразования РФ№1089 от 5 марта 2004 года по математике (базовый уровень);
-федерального перечня учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях реализующих программы общего образования на 2015 – 2016 учебный год№253 от 31.03.14г.
- Примерной программы основного общего образования и авторской программы линии И.И. Зубаревой, А. Г. Мордковича.
- постановления Главного государственного санитарного врача РФ от 29 декабря 2010 года № 189 «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательном учреждениях»»;
- учебного плана МКОУ « Русановская средняя общеобразовательная школа имени В. С. Шатохина»Черемисиновского района Курской области на 2015-2016 учебный год ;
- годового календарного графика школы на 2015-2016 учебный год
За счет уплотнения программного материала или уменьшения количества часов, отводимых на повторение допускается проведение пробного экзамена в форме ЕГЭ.
Основой целью является обновление требований к уровню подготовки выпускников в системе естественно математического образования, отражающее важнейшую особенность педагогической концепции государственного стандарта — переход от суммы «предметных результатов» (то есть образовательных результатов, достигаемых в рамках отдельных учебных предметов) к межпредметным и интегративным результатам. Такие результаты представляют собой обобщенные способы деятельности, которые отражают специфику не отдельных предметов, а ступеней общего образования. В государственном стандарте они зафиксированы как общие учебные умения, навыки и способы человеческой деятельности, что предполагает повышенное внимание к развитию межпредметных связей курса алгебры и начал анализа.
При изучении алгебры и начал анализа в старшей школе осуществляется переход от методики поурочного планирования к модульной системе организации учебного процесса. Модульный принцип позволяет не только укрупнить смысловые блоки содержания, но и преодолеть традиционную логику изучения математического материала: от единичного к общему и всеобщему и от фактов к процессам и закономерностям. В условиях модульного подхода возможна совершенно иная схема изучения математических процессов «все общее — общее — единичное».
Количество часов, на которые рассчитана рабочая программа
Программа составлена в соответствии с объемом учебного времени, отводимым на изучение алгебры и начала анализа по учебному плану образовательного учреждения- 102 ч. в год, 3 ч. в неделю. В том числе на проведение контрольных работ отводится 13 часов.
Содержание учебного предмета
Повторение курса 9 класса (5ч)
Числовые функции (6ч)
Определение и способы задания числовой функции . Область определения и область значений функции. Свойства функций. Исследование функций. Чтение графика. Определение и задание обратной функции. Построение графиков прямой и обратной функции.
Тригонометрические функции (25ч)
Числовая окружность. Длина дуги числовой окружности. Числовая окружность на координатной плоскости. Определение синуса и косинуса на единичной окружности. Определение тангенса и котангенса. Тригонометрические функции числового аргумента. Упрощение тригонометрических выражений. Тригонометрические функции углового аргумента. Решение прямоугольных треугольников. Формулы приведения. Функция y=sin x, её свойства и график. Функция y=cos x, её свойства и график. Периодичность функций y=sin x, y=cos x. Построение графика функций y=mf(x) и y=f(kx) по известному графику функции y=f(x). Функции y=tg x и y=ctg x, их свойства и графики.
Тригонометрические уравнения (10ч)
Определение и вычисление арккосинуса. Решение уравнения cos t=a. Определение и вычисление
арксинуса. Решение уравнения sin t=a. Арктангенс и арккотангенс. Решение уравнений tg x=a, ctg x=a. Простейшие тригонометрические уравнения. Различные методы решения уравнений.
Однородные тригонометрические уравнения.
Преобразование тригонометрических выражений (15ч)
Синус и косинус суммы и разности аргументов. Тангенс суммы и разности аргументов.
Формулы двойного аргумента. Преобразование сумм тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в суммы.
Производная (31ч)
Числовые последовательности и их свойства. Предел последовательности. Сумма бесконечной геометрической прогрессии. Предел функции на бесконечности. Предел функции в точке. Приращение аргумента. Приращение функции. Определение производной. Производная и график функции. Производная и касательная. Формулы для вычисления производных. Производная сложной функции. Применение производной для исследования функций на монотонность и экстремумы.
График функции, график производной. Применениеисследования функций. Построение графиков функций. Задачи с параметром. Графическое решение.
Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на отрезке.
Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке. Текстовые и геометрические задачи на отыскание наибольших и наименьших значений величин.
Обобщающее повторение (10 часов)
Требования к уровню подготовки обучающихся
В результате изучения математики на профильном уровне ученик должен
знать / понимать:
– значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
– идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
– значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
– универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
– различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
– вероятностный характер различных процессов и закономерностей окружающего мира.
Числовые и буквенные выражения
уметь:
– выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; пользоваться оценкой и прикидкой при практических расчетах;
– применять понятия, связанные с делимостью целых чисел при решении математических задач;
– выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами;
– проводить преобразование числовых и буквенных выражений.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
– практических расчетов по формулам, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Функции и графики
уметь:
– определять значение функции по значению аргумента при различных способах задания функции;
– строить графики изученных функций, выполнять преобразование графиков;
– описывать по графику и по формуле поведение и свойства функций;
– решать уравнения, системы уравнений, неравенства; используя свойства функций и их графические представления;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
– описания и исследования с помощью функций реальных зависимостей, представления их графически; интерпретации графиков реальных процессов
.
Начала математического анализа
уметь:
– находить сумму бесконечно убывающей геометрической прогрессии;
– вычислять производные элементарных функций, применяя правила вычисления производных, используя справочные материалы;
– исследовать функции и строить их графики с помощью производной;
– решать задачи с применением уравнения касательной к графику функции;
– решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
– решения прикладных задач, в том числе на наибольшие и наименьшие значения с применением аппарата математического анализа.
Уравнения и неравенства
уметь:
– решать тригонометрические уравнения;
– доказывать несложные неравенства;
– находить приближенные решения уравнений и их систем, используя графический метод;
– решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
– построения и исследования простейших математических моделей.
Календарно – тематический план
| № урока |
Тема урока | Кол-во часов | Дата проведения | Примечание |
| План. | Фактич. |
| Повторение курса 9 класса | 5 |
|
|
|
| 1 | Неравенства и системы неравенств | 1 |
|
|
|
| 2 | Системы уравнений | 1 |
|
|
|
| 3 | Числовые функции | 1 |
|
|
|
| 4 | Элементы комбинаторики, статистики и теории вероятностей | 1 |
|
|
|
| 5 | Входная контрольная работа | 1 |
|
|
|
| Глава 1. Числовые функции | 6 |
|
|
|
|
6-7 | § 1. Определение числовой функции и способы ее задания | 2 |
|
|
|
| 8-9 | §2. Свойства функций | 2 |
|
|
|
| 10-11 | §3. Обратные функции | 2 |
|
|
|
| Глава 2. Тригонометрические функции 25 |
|
| 12-13 | § 4. Числовая окружность | 2 |
|
|
|
| 14-15 | §5. Числовая окружность на координатной плоскости | 2 |
|
|
|
| 16 | Контрольная работа 1 | 1 |
|
|
| 17 | §6. Синус и косинус | 1 |
|
|
|
| 18 | §6. Тангенс и котангенс | 1 |
|
|
|
| 19-20 | § 7. Тригонометрические функции числового аргумента | 2 |
|
|
|
| 21-23 | § 8. Тригонометрические функции углового аргумента | 3 |
|
|
|
| 24-25 | § 9. Формулы приведения | 2 |
|
|
|
| 26 | Контрольная работа №2 | 1 |
|
|
| 27-28 | §10. Функция �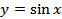 �, ее свойства и график �, ее свойства и график | 2 |
|
|
|
| 29- 30 | §11. Функция �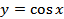 �, ее свойства и график �, ее свойства и график | 2 |
|
|
|
| 31 | §12. Периодичность функций �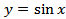 �, � �, �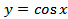 � � | 1 |
|
|
|
| 32-33 | §13. Преобразование графиков тригонометрических функций | 2 |
|
|
|
| 34- 35 | § 14. Функция �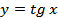 �, � �, �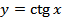 �, их свойства и графики �, их свойства и графики | 2 |
|
|
|
| 36 | Контрольная работа №3 | 1 |
|
|
|
| Глава 3. Тригонометрические уравнения 10 |
|
| 37- 38 | § 15. Арккосинус. Решение уравнения � � � | 2 |
|
|
|
| 39 40 | § 16. Арксинус и решение уравнения �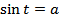 � � | 2 |
|
|
|
| 41
| § 17. Арктангенс и решение уравнения �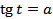 �. �.
Арккотангенс и решение уравнения �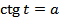 �. �. | .1 |
|
|
|
| 42 | Административная проверочная работа | 1 |
|
|
|
|
43-45 |
§ 18. Тригонометрические уравнения |
3 |
|
|
|
| 46 | Контрольная работа №4 | 1 |
|
|
|
| Глава 4. Преобразование тригонометрических выражений 15 |
|
| 47- 50 | § 19. Синус и косинус суммы и разности аргументов | 4 |
|
|
|
| 51-52 | § 20. Тангенс суммы и разности аргументов | 2
|
|
|
|
| 53- 55
| § 21. Формулы двойного угла | 3 |
|
|
|
| 56- 58
| § 22. Преобразование суммы тригонометрических функций в произведение | 3 |
|
|
|
| 59 | Контрольная работа №5 | 1 |
|
|
| 60
| § 23.1. Преобразование произведений тригонометрических функций в сумму | 1 |
|
|
|
| 61 | § 23.2. Преобразование выражения �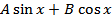 � к виду � � к виду �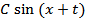 � � | 1 |
|
|
|
| Глава 5. Производная | 31 |
|
|
|
| 62-63 | § 24. Числовые последовательности и их свойства. Предел последовательности | 2 |
|
|
|
| 64-65 | § 25. Сумма бесконечной геометрической прогрессии | 2 |
|
|
|
| 66- 68 | § 26. Предел функции | 3 |
|
|
|
| 69- 71 | § 27. Определение производной | 3 |
|
|
|
| 72- 74 | § 28. Вычисление производных | 3 |
|
|
|
| 75 | Контрольная работа №6 | 1 |
|
|
| 76 78 | § 29. Уравнение касательной к графику функции | 3 |
|
|
|
| 79- 81 | § 30. Применение производной для исследования функций на монотонность и экстремумы | 3 |
|
|
|
| 82- 84 | § 31. Построение графиков функций | 3 |
|
|
|
| 85 | Контрольная работа №7 | 1 |
|
|
| 86- 88
| § 32.1. Применение производной для отыскания наибольшего и наименьшего значений непрерывной функции на промежутке | 3 |
|
|
|
| 89-91
| § 32.2. Задачи на отыскание наибольшего и наименьшего значений величин | 3 |
|
|
|
| 92 | Контрольная работа №8 | 1 |
|
|
|
| 93-95 | Итоговое повторение за курс 10 класса | 3 |
|
|
|
| 96 | Административная проверочная работа | 1 |
|
|
|
| 97 | Повторение. Числовые функции | 1 |
|
|
|
| 98 | Повторение. Тригонометрические функции | 1 |
|
|
|
| 99 | Повторение. Тригонометрические уравнения | 1 |
|
|
|
| 100 | Повторение. Преобразование тригонометрических выражений | 1 |
|
|
|
| 101 | Повторение. Производная | 1 |
|
|
|
| 102 | Итоговая контрольная работа | 1 |
|
|
|
Список литературы
для учителя
А.Г. Мордкович Алгебра и начала анализа.10-11.Методическое пособие для учителя. – М.: Мнемозина, 2005;
Башмаков М.И. Математика. Практикум по решению задач. Учебное пособие для 10 – 11 классов гуманитарного профиля. М., Просвещение, 2005;
Шамшин В.М. Тематические тесты для подготовки к ЕГЭ по математике, Феникс, Ростов-на-Дону,2004;
Студенецкая В.Н. Математика: система подготовки учащихся к ЕГЭ, Волгоград,2004;
Л.А. Александрова Алгебра и начала анализа. Самостоятельные работы 10 класс. – М.: Мнемозина, 2006;
Л.О. Денищева, Т.А. Корешкова. Алгебра и начала анализа, 10 – 11 класс. Тематические тесты и зачеты. – М.: Мнемозина, 2006;
Ф. Ф. Лысенко Математика ЕГЭ – 2007, 2008 . Вступительные экзамены. – Ростов-на-Дону: Легион;
для обучающихся
А.Г. Мордкович Алгебра и начала анализа.10-11 класс. Учебник. – М.: Мнемозина, 2005;
А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская Алгебра и начала анализа.10-11 класс. Задачник. – М.: Мнемозина, 2005;
Ивлев Б.И., Саакян С.И., Шварцбург С.И., Дидактические материалы по алгебре и началам анализа для 11 класса, М., 2000;
Лукин Р.Д., Лукина Т.К., Якунина И.С., Устные упражнения по алгебре и началам анализа, М.1989;
Ковалёва Г.И. Учебно-тренировочные тематические тестовые задания с ответами по математике для подготовки к ЕГЭ, ч. I,II,III, Волгоград,2012;
А.Г. Мордкович, Е.Е. Тульчинская. Алгебра и начала анализа, 10 – 11 класс. Контрольные работы. – М.: Мнемозина, 2005;
Ф. Ф. Лысенко Математика ЕГЭ – 2007, 2008 . Вступительные экзамены. – Ростов-на-Дону: Легион;
С. М. Саакян, А.М. Гольдман, Д.В. Денисов Задачи по алгебре и началам анализа 10-11 класс. – М.: Просвещение, 1990.
14


 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по алгебре и начале анализа (10 класс) (0.25 MB)
Рабочая программа по алгебре и начале анализа (10 класс) (0.25 MB)
 0
0 344
344 17
17 Нравится
0
Нравится
0









