презентация к уроку "Площади фигур"

Квадрат

а)Сторона квадрата равна 10. Найдите его площадь.

б) Периметр квадрата равен 40. Найдите площадь квадрата.

а

1

0

0

№ 1

х

3

х

1

0

а

• 4а = 40, а = 10
• S = 100

1

0

0

№ 2

х

3

х

1

0

Площадь прямоугольника

В прямоугольнике одна сторона равна 6, а диагональ равна 10. Найдите площадь прямоугольника .

A

Решение:

d

b

B

D

a

4

8

№ 3

х

3

х

1

0

Площадь прямоугольника

В прямоугольнике диагональ равна 10, угол между ней и одной

из сторон равен 30 0 , длина этой стороны 5  3 . Найдите

площадь прямоугольника. В ответе запишите S  3.

A

Решение:

d

b



D

B

a

7

5

№ 4

Можно использовать др.способы решения.

х

3

х

1

0

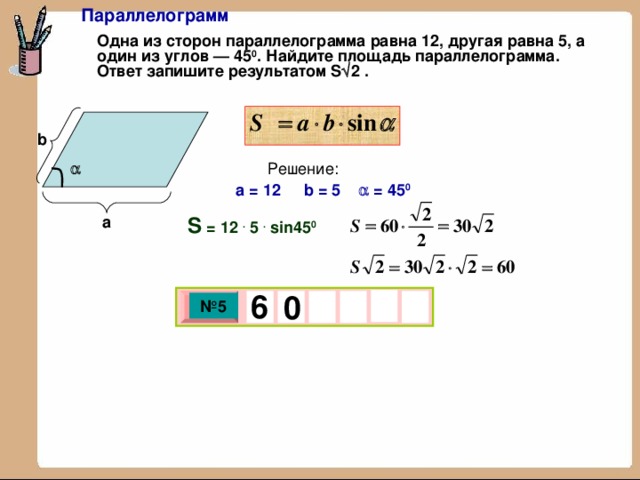
Параллелограмм

Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45 0 . Найдите площадь параллелограмма. Ответ запишите результатом S  2 .

b



Решение:

a = 12 b = 5  = 45 0

а

S = 12 . 5 . sin45 0

6

0

№ 5

х

3

х

1

0

Параллелограмм

Одна из сторон параллелограмма равна 12,

другая равна 5, а косинус одного из углов равен

Найдите площадь параллелограмма.

b

Решение:



a = 12 b = 5

1) Пусть cos  = . Найдем sin 

а

2) S = 12 . 5 . 1/3 = 20

2

0

№ 6

х

3

х

1

0

Ромб

Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.

B

АС = d 1 BD = d 2

Решение:

O

Пусть АВ = 5, АС = d 1 = 6 .

Найдем d 2 = BD.

C

A

В  АОВ (  О = 90 0 ): АВ = 5 (гипотенуза)

АО = АС : 2 = 3 (катет)

По т.Пифагора ВО = 4,  BD = d 2 = 2BO = 8

S = 0,5 . 6 . 8 = 24

D

2

4

№ 7

х

3

х

1

0

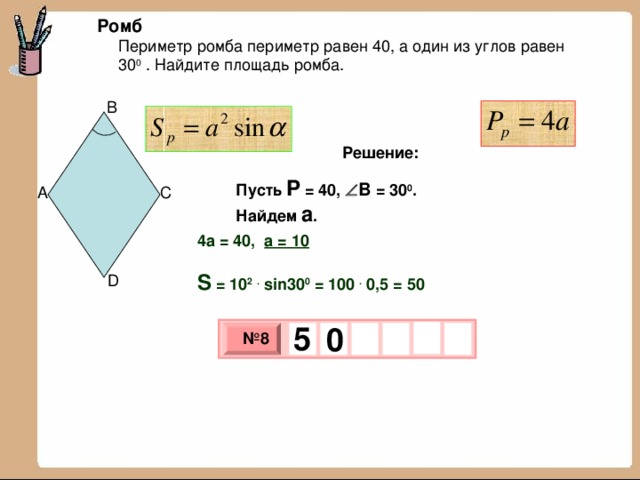
Ромб

Периметр ромба периметр равен 40, а один из углов равен 30 0 . Найдите площадь ромба.

B

Решение:

Пусть P = 40 ,  B = 30 0 .

Найдем а .

C

A

4а = 40, а = 10

S = 10 2 . sin30 0 = 100 . 0,5 = 50

D

5

0

№ 8

х

3

х

1

0

Трапеция

Основания трапеции равны 18 и 12, одна из боковых сторон равна 4  2 , а угол между ней и одним из оснований равен 135 0 . Найдите площадь трапеции.

b

B

C

c

h

Решение:

D

A

Пусть a = 1 8, b = 12, c = 4  3,  АВС = 135 0 .

Найдем ВК = h

K

а

1) В  АВК (  К = 90 0 ): АВ = 4  2 (гипотенуза),

 АВК =  АВС -  СВК = 135 0 – 90 0 = 45 0 ,

6

0

№ 9

х

3

х

1

0

Трапеция

Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен 1/3 . Найдите площадь трапеции.

b

B

C

c

h

Решение:

D

A

Пусть a = 1 8, b = 1 2 , c = 6, sin  В AK = 1/3 .

Найдем ВК = h

K

а

1) В  АВК (  К = 90 0 ): АВ = 6 (гипотенуза),

3

0

№ 10

х

3

х

1

0