
Теорема Пифагора
Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далёкий век.

Задачи исследования :
- Расширение познавательного интереса к изучению геометрии.
- Разносторонний подход к изучению данной темы : как историки, лирики, теоретики и как практики.

Формулировка теоремы
Во времена Пифагора теорема звучала так:
- « Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах»
- « Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».
или

Современная формулировка
« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».

Лирики о теореме Пифагора
Прибудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далёкий век.
Обильно было жертвоприношенье,
Богам от Пифагора сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков
Поэтому всегда с тех самых пор
Чуть истина рождается на свет
Быки ревут, её почуя след
Они не в силах свету помешать
А могут лишь, закрыв глаза дрожать.

Доказательства теоремы
Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.).
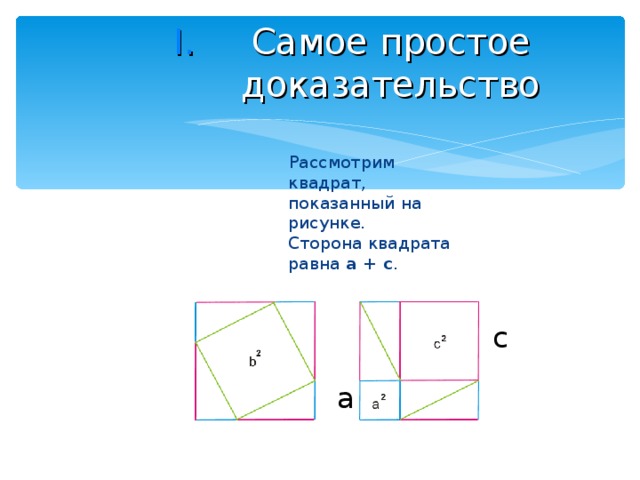
- Самое простое доказательство
Рассмотрим квадрат, показанный на рисунке. Сторона квадрата равна a + c .
c
a
c
a
a
c
c
a
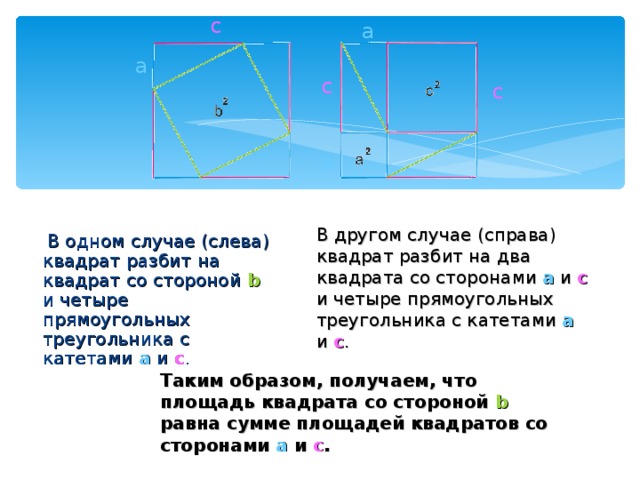
В одном случае (слева) квадрат разбит на квадрат со стороной b и четыре прямоугольных треугольника с катетами a и c .
В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c .
Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c .
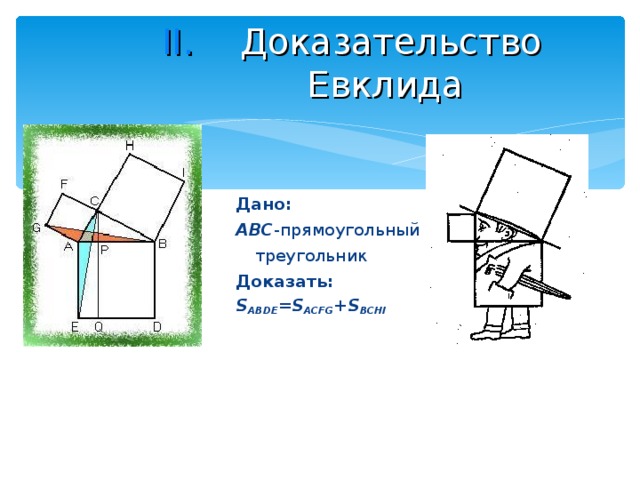
Дано:
ABC -прямоугольный треугольник
Доказать:
S ABDE =S ACFG +S BCHI
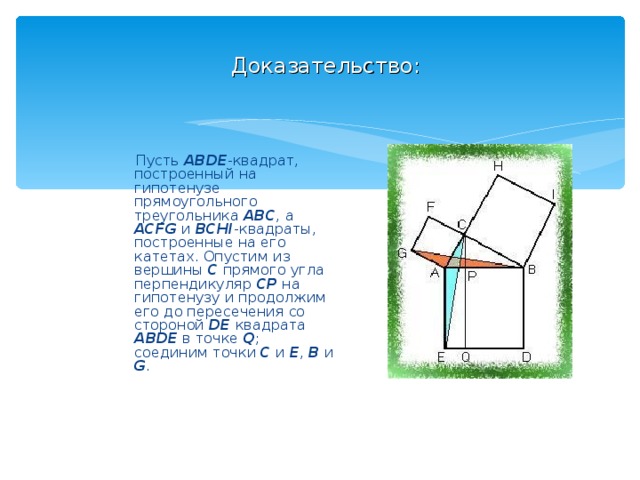
Доказательство:
Пусть ABDE -квадрат, построенный на гипотенузе прямоугольного треугольника ABC , а ACFG и BCHI -квадраты, построенные на его катетах. Опустим из вершины C прямого угла перпендикуляр CP на гипотенузу и продолжим его до пересечения со стороной DE квадрата ABDE в точке Q ; соединим точки C и E , B и G .
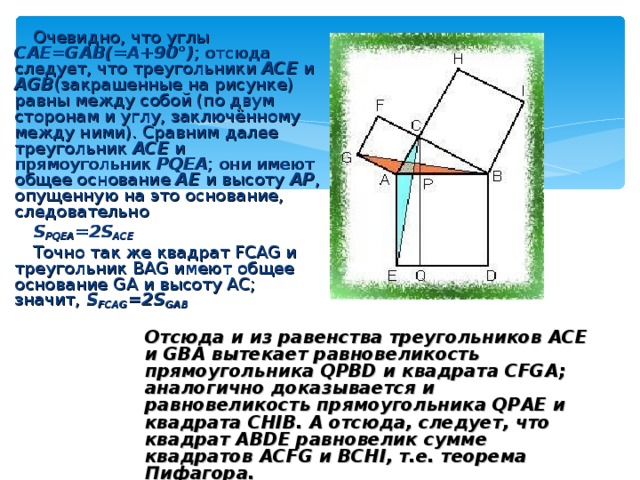
Очевидно, что углы CAE=GAB(=A+90°) ; отсюда следует, что треугольники ACE и AGB (закрашенные на рисунке) равны между собой (по двум сторонам и углу, заключённому между ними). Сравним далее треугольник ACE и прямоугольник PQEA ; они имеют общее основание AE и высоту AP , опущенную на это основание, следовательно
S PQEA = 2S ACE
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, S FCAG =2S GAB
Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.

- Алгебраическое доказательство
Дано: ABC -прямоугольный треугольник
Доказать: AB 2 =AC 2 +BC 2
Доказательство:
1) Проведем высоту CD из вершины прямого угла С . 2) По определению косинуса угла соsА=AD/AC=AC/AB , отсюда следует
AB•AD=AC 2 .
3) Аналогично соsВ=BD/BC=BC/AB , значит
AB•BD=BC 2 .
4) Сложив полученные равенства почленно, получим:
AC 2 +BC 2 = АВ •(AD + DB)
AB 2 =AC 2 +BC 2 . Что и требовалось доказать.

- Геометрическое доказательство
Дано: ABC -прямоугольный треугольник
Доказать: BC 2 =AB 2 +AC 2
Доказательство:
1) Построим отрезок CD равный отрезку AB на продолжении катета AC прямоугольного треугольника ABC . Затем опустим перпендикуляр ED к отрезку AD , равный отрезку AC , соединим точки B и E . 2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников:
S ABED =2AB·AC/2+BC 2 /2
3) Фигура ABED является трапецией, значит, её площадь равна:
S ABED = (DE+AB)·AD/2.
4) Если приравнять левые части найденных выражений, то получим:
AB·AC+BC 2 /2=(DE+AB)(CD+AC)/2
AB·AC+BC 2 /2= (AC+AB) 2 /2
AB·AC+BC 2 /2= AC 2 /2+AB 2 /2+AB·AC
BC 2 =AB 2 +AC 2 .
Это доказательство было опубликовано в 1882 году Гэрфилдом.
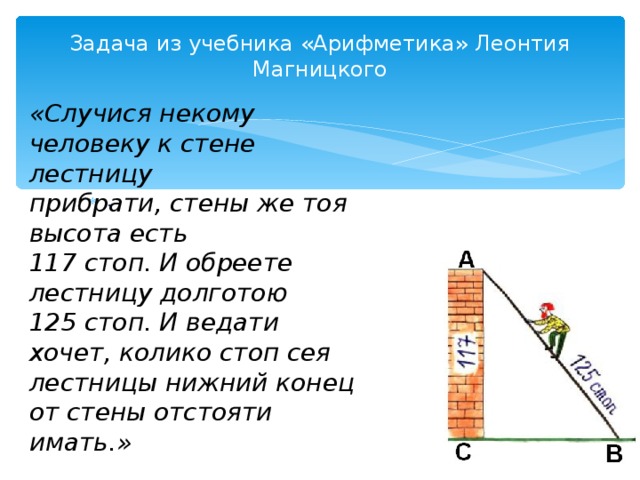
Задача из учебника «Арифметика» Леонтия Магницкого
«Случися некому человеку к стене лестницу
прибрати, стены же тоя высота есть
117 стоп. И обреете лестницу долготою
125 стоп. И ведати хочет, колико стоп сея
лестницы нижний конец от стены отстояти
имать.»

Изречения Пифагора
- Статуя формой своей хороша, А человека украсят дела.
- Шуткой беседу укрась, освети. Шутка, что соль. Лишь не пересоли…
- Лучше молчи, ну, а коль говоришь, Пусть будет лучше, чем то, что молчишь.
- Если ты в гневе, не смей говорить! Действовать резко и злобу сорить.
- Пред тем, как станешь говорить, пусть мысль созреет Под языком твоим. Созревшая - все смеет.

Чему равна сумма квадратов чисел?
а) 3 2 +4 2 =
б) ( ) 2 + ( ) 2 =
9+16=25
5+7=12

Верно ли решение?
3 2 +4 2 =(3+4) 2
нет

Чему равно?
(а+в) 2 =
а 2 +2ав+в 2

Какой треугольник изображен на рисунке?
Равнобедренный
Какой треугольник изображен на рисунке?
Равносторонний
а
а
а

Какой треугольник изображен на рисунке?
А
Прямоугольный
В
С
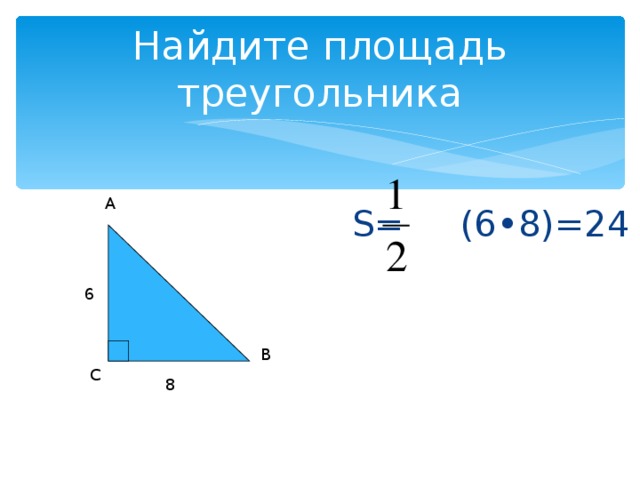
Найдите площадь треугольника
S= (6 • 8)= 24
А
6
В
С
8
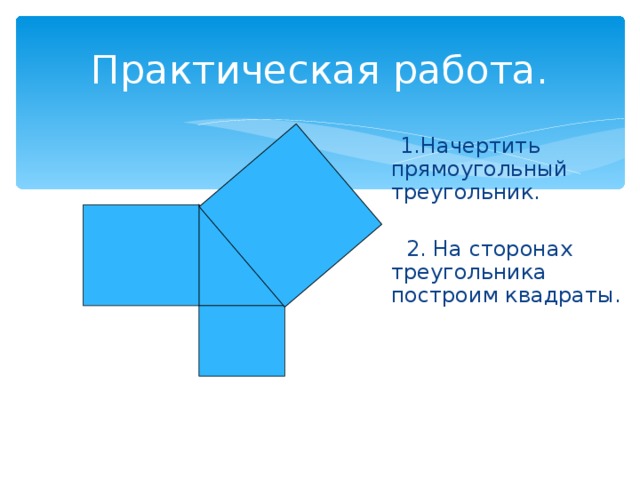
Практическая работа.
1.Начертить прямоугольный треугольник.
2. На сторонах треугольника построим квадраты.
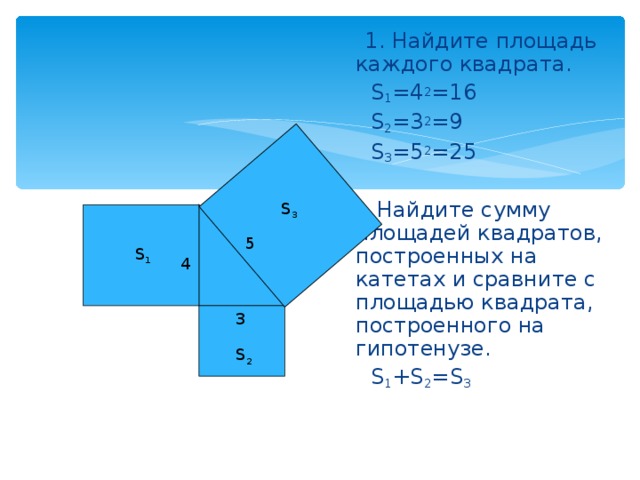
1. Найдите площадь каждого квадрата.
S 1 =4 2 =16
S 2 =3 2 =9
S 3 =5 2 =25
2. Найдите сумму площадей квадратов, построенных на катетах и сравните с площадью квадрата, построенного на гипотенузе.
S 1 + S 2 = S 3
S 3
5
S 1
4
3
S 2

Вывод:
Площадь квадрата построенного на гипотенузе прямоугольного треугольника равна сумме площадей квадратов, построенных на катетах.
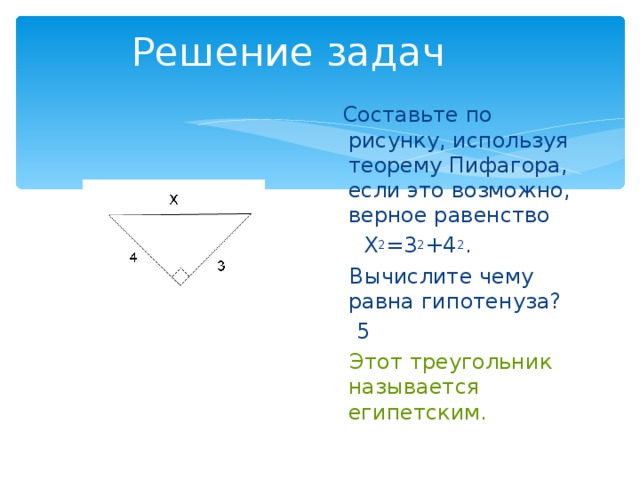
Решение задач
Составьте по рисунку, используя теорему Пифагора, если это возможно, верное равенство
Х 2 =3 2 +4 2 .
Вычислите чему равна гипотенуза?
5
Этот треугольник называется египетским.

Значение теоремы Пифагора
Теорема Пифагора- это одна из самых важных теорем геометрии. Значение её состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии .
Друзья я бы мог бы еще найти очень много доказательств, но думаю этого достаточно, ведь все мы знаем что Пифагор обладал не только внешней красотой, но его идеи замыслы были еще красивее.

Выполненная задача :
- Обобщить и систематизировать знания по теме, учиться воспринимать материал в целостной системе различных предметов.

Память .
- Памятник Пифагору находится в порту города Пифагория и напоминает всем о теореме Пифагора, наиболее известном его открытии. Катет, лежащий в основании треугольника - мраморный , гипотенуза и фигура самого Пифагора в виде второго катета - медные.

Афоризмы.
«Не садись на хлебную меру» С равным достоинством относись к малым и великим мира сего.
«Через весы не шагай» Не нарушай равновесия в природе.
«Будь с тем, кто ношу взваливает, не будь с тем, кто ношу сваливает» Дружбу держи с кем мудрость постигаешь, чурайся глупцов, кто праздно время проводит.
«Ласточек в доме не держи» Не замыкайся в себе, что знаешь, свободной судьбе предоставь.
«Не ешь сердца» Не ничтожь счастье других и не терзай себя душевными муками.
«Корми петуха, но не приноси его в жертву, поскольку посвящен он Солнцу и Луне» Соразмерно чти и храни вожака и правителя, но не поступай вероломно, не предавай.
«Меру во всем соблюдай и дела свои во время делай»
«Начало – пол-целого дела»

Немало важное
- Пифагор первым определил и изучил
- взаимосвязь музыки и математики.
- Пифагор рассматривал геометрию не как практическую и прикладную дисциплину, а как логическую науку.
- Система морально-этических правил, завещанная Пифагором, была собрана в своеобразный моральный кодекс пифагорейцев «Золотые стихи».
- Во Франции и некоторых областях Германии в Средневековье теорему Пифагора называли «Мостом слов», а у математиков арабского Востока – «Теоремой невесты».

1. http://ppt4web.ru
2.http://ru.wikipedia.org
- «Арифметика» Леонтия Магницкого
- стихи немецкого писателя А. Шамиссо


 Получите свидетельство
Получите свидетельство Вход
Вход











































 Презентация по математике "Теорема Пифагора" (1.77 MB)
Презентация по математике "Теорема Пифагора" (1.77 MB)
 0
0 540
540 71
71 Нравится
0
Нравится
0








