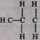Знаменитая теорема Пифагора

Цель урока: Знакомство с биографией и теоремой Пифагора и ее практическое применение.

Задачи:

Формирование общеучебных навыков и умений, формулировка и доказательство теоремы Пифагора.

Применение теоремы в решении задач.

Развитие познавательного интереса.

Повышение мотивации обучения.

Осуществление межпредметных связей с алгеброй, географией, историей, информатикой.

Развитие психических процессов: внимания, мышления, воображения.

Воспитание коллективного труда, взаимопомощи, трудолюбия, аккуратности в работе

Оборудование: компьютер,  проектор, презентация.

«Геометрия владеет двумя сокровищами: одно из них –это теорема Пифагора» 

                                                                          Иоганн Кеплер

                                            Ход урока:

1.Организационный момент

Приветствие и вступительное слово учителя.

Добрый день. На этом уроке подведем итог нашим исследованиям и полученным знаниям о великом Пифагоре и  его знаменитой теореме. Проверим, как вы сможете применить свои знания при решении различных простейших, исторических и геометрических задач. Перед тем как приступим к расширению знаний о Пифагоре и его теореме, вспомним пройденный материал.

2.Актуализация прежних знаний.

1.Какой треугольник называется прямоугольным?

2.Как называются стороны прямоугольного треугольника?

3.Какая сторона прямоугольного треугольника называется гипотенузой?   

4.Какие стороны называются катетами?

Задача№1.

Стороны прямоугольника 2,8дм и 13см. Найти площадь и периметр.

Задача№2.

Периметр прямоугольника равен 4дм. Одна из его сторон равна 12см. Найдите другую сторону.

Задача №3.

 Катеты прямоугольного треугольника равны 140мм и 0,8дм. Найдите площадь прямоугольного треугольника.

3. Исторический экскурс

Давайте послушаем и посмотрим исторический материал, который приготовили наши ученики о Пифагоре. (слайды 2-12)

-Пифагор Самосский (ок.580 – ок. 500 до н.э.) древнегреческий математик и философ- идеалист.  Родился на острове Самос, расположенным у самых берегов Малой Азии. От путешественников и капитанов кораблей он узнавал о близких и далеких чудесных странах Египта и Вавилонии, мудрость жрецов которых изумляла молодого Пифагора и манила. Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове. Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет. Сначала приплыл к берегам Египта, прошел его вдоль и поперек. Внимательно присматривался к окружающим, прислушивался к жрецам. В Египте прожил 22 года. Хорошо овладев всеми науками египтян. В Египте Пифагор попал в плен к Камбизу, персидскому завоевателю, и его увезли в Вавилон. Пифагор знал, что это величайший город мира. Грандиозная панорама города, раскинувшего свои дворцы и высокие оборонительные стены по обоим берегам Ефрата привели Пифагора в восторг и изумление. Вавилон не шел в сравнение ни с одним греческим городом. Пифагор быстро освоился со сложными вавилонскими традициями, он жадно впитывает речи халдейских жрецов. Сам составляет таблицы расположения звезд и небесных явлений. Узнает о правилах решения некоторых уравнений, квадратных и кубических. Здесь, наверно, он узнает, что сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины гипотенузы. У халдейских магов изучает теорию чисел. И, может быть, отсюда пошла та числовая мистика, приписывая числам божественные силы, которая Пифагором была преподнесена как философия. Предания приписывают Пифагору посещение и Индии. Возвратившись на родину, Пифагор попытался организовать свою школу. Однако по неизвестным причинам, он вскоре оставляет Самос и селится в Кротоне. Здесь Пифагору удалось организовать свою школу, которая действовала почти 30 лет. В основу философии пифагорейского союза было положено мистическое учение о числе. Открытие того, что между стороной и диагональю квадрата не существует общей меры, было самой большой заслугой пифагорейцев. Пифагору еще приписывают еще ряд важных открытий, а именно: теорему о сумме внутренних углов треугольника; задачу о делении плоскости на правильные многоугольники. Основной особенностью метода Пифагора было объединение геометрии с арифметикой. Пифагор один из первых считал, что Земля имеет форму шара и является центром вселенной, что Солнце и Луна и планеты имеют собственное движение, отличное от суточного движения неподвижных звезд.

         Что уж говорить об отдельных фактах биографии великого математика.  Рассказывали, что он мог изменить направление полета птиц. Он разговаривал с животными. Однажды переходя вброд реку, Пифагор вознес молитву духу реки, и из воды послышался голос: « Приветствую тебя, Пифагор!» Говорили также, что он повелевал  духами: посылал их в воду и, глядя на рябь, делал предсказания. Он умудрялся исцелять людей. Знал лекарственные свойства огромного количества растений. Фигура Пифагора была окружена множеством легенд: его считали перевоплощенным богом Аполлоном, полагали, что у него было золотое бедро, и он был способен раздваиваться и запросто в одно и то же время преподавать в двух разных местах. Пифагору повезло больше, чем другим ученым древности. С его именем многое связано в математике и конечно же его знаменитая теорема Пифагора.

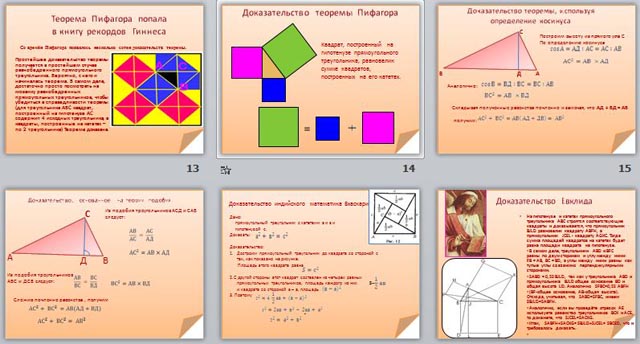
4.Теорема Пифагора (слайды 13-15)

   Доказательство теоремы ( один случай, используя определение косинуса)

   Ребята рассказывают, что это доказательство не единственное, есть очень                   

    много  доказательств, а это некоторые из них. (слайды 16 – 18)       

5.Практическое применение теоремы Пифагора. (слайд 20)

6.Решение задач, используя теорему. (слайд 21-23)

7.Самостоятельная работа  (слайд24)

    Решить задачи на два варианта.

    Первый вариант : задачи № 1 и № 3

    Второй вариант: задачи № 2 и №4

    Кто быстрее справиться с заданием выполняет задачу №5.

8.Область применения теоремы (слайд 25)

9.Значение теоремы Пифагора (слайд 26-28)

10.Рефлексия. Итог занятия.

     Мне приятно, что вы серьезно отнеслись к этой работе. Молодцы!