Цели урока:
1. Подвести учащихся к выводу теоремы Пифагора путём измерительных работ и логических рассуждений, доказать теорему Пифагора, формировать практические навыки применения данной теоремы.
2. Способствовать развитию гибкости мышления, умений анализировать, устанавливать связи ранее изученного материала с новым и осуществлять доказательные рассуждения.
3. Воспитывать культуру общения, умение вести дискуссию. Прививать устойчивый интерес к изучению математики , показывая красоту математических доказательств, их стройность, логичность. Создать условия для расширения общего кругозора учащихся, используя исторический материал.
Тип урока: урок изучения и первичного закрепления новых знаний.
Оборудование: ( мультимедийный проектор, компьютер, экран, презентация, портрет Пифагора).
ХОД УРОКА
1. Организационный момент. (3мин)
Ребята, я рада видеть вас на нашем уроке и предлагаю вам перенестись в Древнюю Грецию и стать учениками пифагорейской школы. Мне хотелось бы узнать с каким настроением, вы отправляетесь в путешествие. Мне приятно, что в основном у вас хорошее или отличное настроение, я обещаю, что к концу урока оно не испортится.
Презентация
На доске написана тема урока, портрет Пифагора, изображение пирамид и прямоугольных треугольников.
Учитель: Ребята, внимательно посмотрите на доску и ответьте на вопросы:
- Как вы думаете, что нам предстоит сделать сегодня на уроке?
- А для чего мы будем изучать эту теорему?
- Как вы думаете, почему она называется именно так? -
Кто - нибудь слышал имя этого ученого?
II. Вступительное слово учителя.
Таким образом подведем итог ваших размышлений. И так во время путешествия мы изучим одну из важнейших теорем геометрии – теорему Пифагора. Эта теорема является основой для решения многих геометрических задач и базой изучения теоретического материала в курсе геометрии 7 - 11класса.
III. Актуализация знаний. (10мин)
Учитель: Открыли рабочие тетради, записали число, классная работа, тема урока:
" Теорема Пифагора".
Для того чтобы наша работа была успешной, повторим некоторые геометрические факты.
- Сформулируйте определение прямоугольного треугольника?
- Как называются стороны прямоугольного треугольника?
- Формула площади прямоугольного треугольника?
- Формула площади квадрата?
- Свойство площадей?
Слайд 2– прямоугольный треугольник.
Слайд 3 – площадь квадрата.
Учитель: При решении геометрических задач нам приходится находить длины сторон прямоугольного треугольника, всегда ли это возможно? Постройте в тетради прямоугольный треугольник, катеты которого равны 3см и 4см. Можно ли вычислить длину гипотенузы? (учащиеся высказывают свои предположения, наверняка появится версия, что гипотенузу можно измерить, пользуясь линейкой).
Учитель: Т. о практическим путем мы установили , если катеты прямоугольного треугольника равны 3см и 4см, то гипотенуз равна 5см. В геометрии такой треугольник называют египетским треугольником.
Всегда ли можно пользоваться этим способом для нахождения гипотенузы?
Ученики: Этим способом можно пользоваться, только при малых длинах.
Учитель: По всей видимости надо установить закономерность между сторонами прямоугольного треугольника, для этого решим практическую задачу.
Практическая работа исследовательского характера.
(работа в парах)(Слайд 4).
Построить прямоугольные треугольники с катетами:
Измерить гипотенузу, результаты занести в таблицу.
|
a |
12 |
6 |
8 |
|
b |
5 |
8 |
15 |
|
c |
13 |
10 |
17 |
Учитель: Постараемся выразить формулой зависимость между длинами катетов и гипотенузой в прямоугольных треугольниках.
Ученики выдвигают свои гипотенузы, которые обсуждаются.
Учитель: Попытаемся установить соответствие между квадратами длин катетов и квадратом длины гипотенузы. ( для всех трех условий аналогичные рассуждения)
|
|
длины |
квадраты длин |
|
a |
12 |
144 |
|
b |
5 |
25 |
|
c |
13 |
169 |
Учитель: Проанализируйте числовые значения в последнем столбике. Какую закономерность мы наблюдаем?
Ученики: "В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы".
Учитель: Аналогическую закономерность установил древнегреческий ученый Пифагор, его открытие назвали Теоремой Пифагора, существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т. д. ). Чуть позже мы рассмотрим одно из доказательств, приведенных в учебнике.
Слайд 5, 6. Сейчас послушаем рассказ о математике, именем которого она названа.
( сообщение ученика). ( 3мин)
ПИФАГОР САМОССКИЙ (ок. 580 – ок. 500г. до н. э. )
О жизни Пифагора известно немного. Он родился в 580 г. до н. э. в Древней Греции на острове Самос, который находится в Эгейском море, поэтому его называют Пифагором Самосским.
В молодости Пифагор был учеником Фалеса, побывал в Египте, где учился у жрецов.
В 530 г. до н. э. Пифагор основал так называемую пифагорейскую школу. Около сорока лет учёный посвятил себя, созданной им школе. Учеников школы называли пифагорейцами. Они занимались не только математикой, но и философией, естественными науками.
Известно также, что кроме духовного и нравственного развития учеников Пифагора заботило их физическое развитие. Он не только сам участвовал в Олимпийских играх и два раза побеждал в кулачных боях, но и воспитал плеяду великих олимпийцев.
Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя.
Физминутка(2мин)
IV. Этап усвоения новых знаний и способов действий. (10мин)
Работа над теоремой( на основе сотрудничества с учащимися).
Слайд 7 - «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов» с2 = а2 +b2(доказательство выполняют у доски).
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход



 Площадь квадрата равна
Площадь квадрата равна
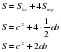
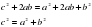









 Урок математики "Теорема Пифагора" (40.51 КB)
Урок математики "Теорема Пифагора" (40.51 КB)
 0
0 1452
1452 96
96 Нравится
0
Нравится
0


