Цели:
1. Образовательная - познакомить учащихся с теоремой Пифагора и научить ее применять к решению задач.
2. Развивающая - развивать мыслительные способности учащихся посредством вовлечения их в обсуждение проблемы.
3. Воспитательная – прививать устойчивый интерес к изучению математики, воспитывать культуру общения, умение вести дискуссию.
План урока:
I. Создание проблемной ситуации.
II. Теорема Пифагора. Различные способы доказательства.
III. Решение задач.
IV. Итог урока.
Оборудование:
1. Персональный компьютер
2. Мультивидеопроектор, экран
3. Презентация для урока
4. Чертежные инструменты
- Орг. момент.
- Начало урока: наш урок мы начнем с решения одной старинной задачи. (слайд №2)
Задача. На обоих берегах реки растет по пальме, одна против другой. Высота одной 30 локтей, другой – 20 локтей. Расстояние между их основаниями – 50 локтей. На верхушке каждой пальмы сидит птица. Внезапно обе птицы заметили рыбу, выплывшую к поверхности воды между пальмами. Они кинулись к ней разом и достигли ее одновременно. На каком расстоянии от более высокой пальмы появилась рыба?
Переведем задачу на математический язык. (слайд №3)
Учитель: Что означает, что птицы летели с одинаковой скоростью и догнали рыбу одновременно?
1 ученик: Это означает, что до рыбы они пролетели одинаковое расстояние, т. е. СЕ=ДЕ.
Учитель: Что требуется найти в задаче?
2 ученик: Найти АЕ.
Учитель: Какой способ для решения задачи вы предлагаете?
3 ученик: С помощью уравнения. За Х можно принять расстояние АЕ. Тогда ВЕ=50 - Х.
Учитель: Какие величины надо выразить через Х, чтобы мы могли составить уравнение?
4 ученик: Надо выразить СЕ и ДЕ.
Учитель: Можем ли мы это сделать?
1 ученик: Нет, мы не можем это сделать.
Учитель: Что мы можем сказать о треугольниках АСЕ и ВДЕ?
2 ученик: Они прямоугольные.
Учитель: Как называются стороны АС и АЕ в треугольнике АСЕ, ВД и ВЕ в треугольнике ВДЕ?
3 ученик: Они называются катетами.
Учитель: Как называются стороны СЕ и ДЕ?
4 ученик Они называются гипотенузами.
Учитель: Значит, нам надо знать зависимость между катетами и гипотенузой в прямоугольном треугольнике. (слайд №4)
Эту зависимость подметили еще в глубокой древности и доказали теорему, которую знают теперь почти все школьники. Эта теорема носит имя Пифагора. Послушайте историческую справку. (слады №№5 - 9)
Пифагор - это не имя а прозвище, данное ему за то, что он высказывал истину также постоянно, дельфийский аракул, («Пифагор» значит «убеждающий речью») жил в Древней Греции (родился он в 580 г. до н. э. , умер в 500 г. до н. э. ). О жизни этого ученого известно немного, зато с его именем связан ряд легенд. Рассказывают, что он много путешествовал: был в Индии, Египте, Вавилоне; изучал древнюю культуру и достижения науки разных стран. Вернувшись на родину, Пифагор организовал кружок молодежи из представителей аристократии. В пифагорейский союз, который имел свой кодекс чести, принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения своего основателя. Пифагорейцы занимались математикой, философией, естественными науками. Ими было сделано много важных открытий в арифметике и геометрии. Авторство всех работ приписывалось Пифагору. Заповеди Пифагора и его учеников актуальны и сейчас и могут быть приемлемы для любого здравомыслящего человека. Вот они:
- делать то, что впоследствии не огорчит тебя и не принудит раскаиваться;
- не делай никогда того, что не знаешь, но научись всему, что следует знать;
- не пренебрегай здоровьем своего тела;
- приучайся жить просто и без роскоши.
Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили имя своего учителя множеством легенд.
Физкультминутка (слайд №10)
Представим себе, как могли решать нашу проблему ученики Пифагора на одном из заседаний своего союза. (инсценировка)
Попробуем найти зависимость между гипотенузой и катетами в прямоугольном треугольнике практическим путем.
Пифагор дает задание каждому из участников представления:
- Ты построй треугольник с катетами 3 и 4. (1 ученик)
- Ты – 6 и 8. (2 ученик)
- Ты – 8 и 15. (3 ученик)
- Ты – 12 и 5. (4 ученик)
Измерим длину гипотенузы в каждом треугольнике и данные занесем в таблицу:
|
a |
3 |
6 |
8 |
12 |
|
b |
4 |
8 |
15 |
5 |
|
c |
5 |
10 |
17 |
13 |
Пифагор: Какую зависимость видит каждый из вас?
Смотрите документ.
Пифагор: Будет ли это верно для других случаев?
1, 2 ученики: Нет.
Пифагор: Значит, ни одна из формул не выражает зависимость между гипотенузой и катетами в прямоугольном треугольнике.
4 ученик: Я заметил, что 122+52=132, 144+25=169. Может, это будет верно и для других случаев?
Пифагор: Давайте проверим.
|
a2 |
9 |
36 |
64 |
144 |
|
b2 |
16 |
64 |
225 |
25 |
|
c2 |
25 |
100 |
289 |
169 |
1, 2, 3 ученики: Действительно, это так.
II. Пифагор: Значит a2+b2=c2. Попробуем доказать это.
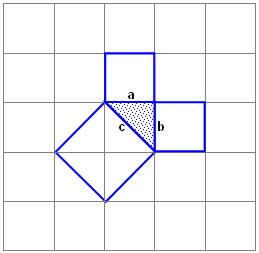
Построим на сторонах прямоугольного треугольника квадраты со сторонами a, b, c. (слайд№11)
Что означает запись a2?, площадь квадрата со стороной a; b2 ?, площадь квадрата со стороной b; c2 - ?, площадь квадрата со стороной с.
Пифагор: Попробуйте сформулировать теорему. (слайд №12)
1 ученик: Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах. (слайд №13)
Учитель: Так звучала теорема во времена Пифагора.
2 ученик: Квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов его катетов.
Учитель: А так звучит современная формулировка. (слайд №14)
Пифагор: Друзья, обдумайте возможные доказательства этой теоремы. Того, кто придумает лучший способ, ждет награда.
Учитель: К настоящему времени известно более 200 способов доказательства этой теоремы. Посмотрим, какие из них предложили ученики Пифагора.
1 ученик: Квадраты, построенные на катетах, состоят из двух одинаковых треугольников. А квадрат, построенный на гипотенузе, состоит из четырех таких треугольников. Значит, теорема верна, все очень просто. (слайд №15)
2 ученик: Просто и красиво, молодец друг.
3 ученик: Просто и красиво, но ведь ты взял не обычный прямоугольный треугольник.
1 ученик: Что же в нем необычного?
3 ученик: Ты привел доказательство для равнобедренного прямоугольного треугольника. А будет ли оно верно, если a≠b?
1 ученик: Да, пожалуй ты прав. Я подумаю еще.
2ученик: А я кажется, придумал. Если закрасить 4 треугольника на первом рисунке, то останется квадрат площадью c2, а если такие же 4 треугольника закрасить на втором рисунке, то останутся квадраты площадью a2 и b2. Вот и получается, что c2=a2+b2. (слайд №16)
3 ученик: Верно, верно. Я использовал этот же прием, но по - другому. Поставил рядом квадраты площадью a2 и b2. Теперь отрежем от них два одинаковых треугольника с катетами a и b и гипотенузой с, и переложим так, как показано на рисунке. Получим квадрат площадью с2. Значит, опять получается, что a2+b2=c2. (слайд №17 - 18)
Пифагор: Вам обоим удалось решить эту проблему. Притом вы предложили действительно простое и красивое доказательство. В этом и состоит самый лучший математический стиль – посредством остроумного построения сделать неочевидное очевидным.
Учитель: Ребята, вы тоже можете подумать дома и предложить свои способы доказательства теоремы Пифагора.
4 ученик: А я не смог неочевидное очевидным, но я доказал теорему, используя уже известные, ранее доказанные факты. (слайд №19)
Дано: ΔАВС – прямоугольный. Угол с=900; АС = в, АВ = с, ВС = а.
Доказать, что а2+в2=с2.
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход





 ученик: А я кажется, придумал. Если закрасить 4 треугольника на первом рисунке, то останется квадрат площадью c2, а если такие же 4 треугольника закрасить на втором рисунке, то останутся квадраты площадью a2 и b2. Вот и получается, что c2=a2+b2. (слайд №16)
ученик: А я кажется, придумал. Если закрасить 4 треугольника на первом рисунке, то останется квадрат площадью c2, а если такие же 4 треугольника закрасить на втором рисунке, то останутся квадраты площадью a2 и b2. Вот и получается, что c2=a2+b2. (слайд №16)












 Коснпект урока по математике на тему "Теорема Пифагора" (0.18 MB)
Коснпект урока по математике на тему "Теорема Пифагора" (0.18 MB)
 0
0 590
590 7
7 Нравится
0
Нравится
0


