Операции над множествами

Исследовательская работа по теме «Множества и операции над ними»

Работу выполнил

ученик 6 класса

МАОУ «ФМШ №56» г. Улан-Удэ

Агафонов Даниил

Руководитель:

Г.Н.Шмакова

учитель математики

высшей квалификационной категории

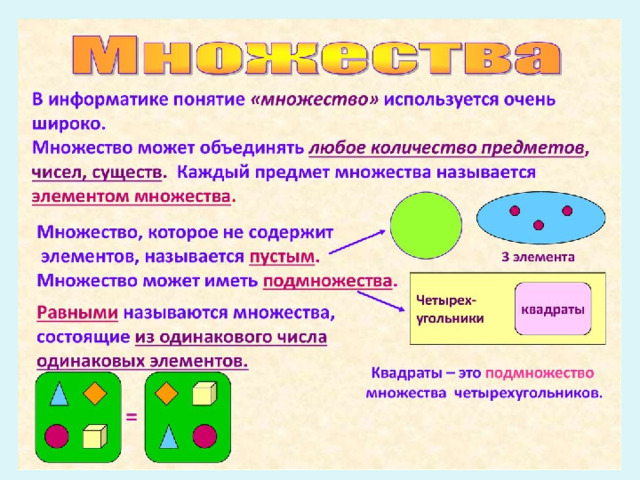
• Каждый человек встречается с множествами, иногда сам того не зная. Множество простых, составных чисел, остроугольных треугольников, объемных фигур. Эти понятные и простые множества всегда с нами.

Но как много знают о множествах ученики моего класса? Считают ли они эту тему ненужной или скучной? Знают ли они, где множества находят применение? На эти и другие вопросы я хочу ответить своей работой.

Выбор темы исследования

• Выяснить что же такое множества, научиться производить операции над ними, изучить специальные знаки, используемые в этой области, а также научиться решать задачи с множествами.

• Определить степень знаний учеников моего класса по этой теме, их отношение к ней.

Цель исследования

• 1.Проанализировать интернет-ресурсы по данной теме
• 2. Выяснить, какие действия над множествами существуют
• 3. Рассмотреть применение теории множеств при решении задачи
• 4. Научиться составлять задачи с множествами
• 5.Провести опрос одноклассников, доказать гипотезу

Задачи исследования

Ученики моего класса мало знают о множествах, их применении и решении задач с ними. После ознакомления с теорией множества и операциями над ними, они поймут, что:

• решения задач на множества основывается на логике;
• операции над множествами не отличаются от обычных математических операций.

Гипотеза исследования

Актуальность

Научный подход данной темы и практическое использование . Работа знакомит с понятием множества и операциями над множествами, раскрывает аксиоматическую теорию множеств.

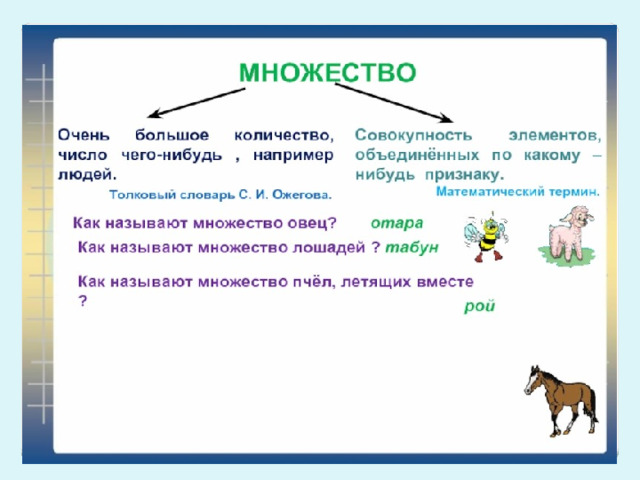
Представленная работа знакомит с понятием множества с помощью простых примеров из окружающей деятельности. Даны определения операциями для множествами: объединение, пересечение, равные множества, которые наглядно проиллюстрированы диаграммами Эйлера Венна и рассмотрены на конкретных примерах.

Теория множеств используется на уроках при решении систем уравнений систем неравенств, нахождение области определения, а также решений логических задач. Широкое применение имеют операции над множествами и аксиоматическое исследование.

Объединение множеств

A=

15; 30; 45; 60; 75; 90

множество двузначных чисел кратных 15

B=

15; 18; 30; 36; 45; 54; 60; 72; 75; 90

множество двузначных чисел кратных 18

15; 18; 30; 36; 45; 54; 60; 72; 75; 90

Множество состоящие из элементов этих множеств образует их объединение

№ п/п

Вопросы

Опрошено

1.

_25___ человек

Опрошено

Как вы считаете, хорошо ли вы знаете тему «множества»?

до

_25___ человек

а) Хорошо

после

3

б) Средне

в) Плохо

2.

17

7

5

15

Отличаются ли операции над множествами от обычных математических?

3

а) Да, сильно

11

б) Да, немного

3.

в) Нет

8

2

7

6

Какие методы решения задач на множества вы знаете?

16

а) Стандартные

4

б) Решаю на основе логики

4.

15

2

в) Затрудняюсь ответить

Сможете ли вы четко сформулировать ваш способ решения?

5

19

5

а) Да

5

б) Нет

20

16

9

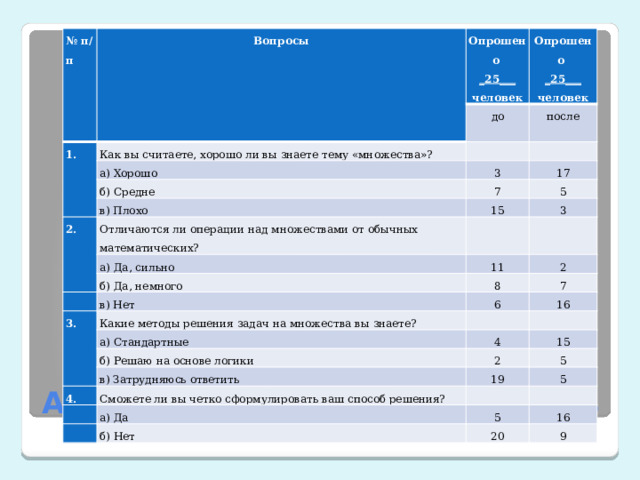
Анкетирование одноклассников

Аксиоматическая теория множеств.

Современная теория множеств строится на системе аксиом — утверждений, принимаемых без доказательства, — из которых выводятся все теоремы и утверждения теории множеств.

Эта система аксиом записана на языке логики первого порядка, и содержит бесконечное количество аксиом. Существуют и другие, конечные системы. Например, система NBG наряду с множествами рассматривает так называемые классы объектов. NBG равносильна ZF в том смысле, что любая теорема о множествах (то есть не упоминающая о классах), доказуемая в одной системе, также доказуема и в другой.

• Сложение – Пересечение.
• Операция пересечение (обозн. ⋂) – при выполнении для множеств А и В,
• Получаем множество С, содержащее элементы, принадлежащие и А, и В одновременно.
• Сложение – Объединение.
• Операция объединение (обозн. ∪) – при выполнении для множеств А и В, получаем множество С, содержащее элементы, принадлежащие или А, или В.
• Вывод.
• Арифметическое действие «Сложение» интерпретируется операциями «Пересечение» и «Объединение», с различными результатами.
• То есть имеет место различие .
•  

Операции над множествами

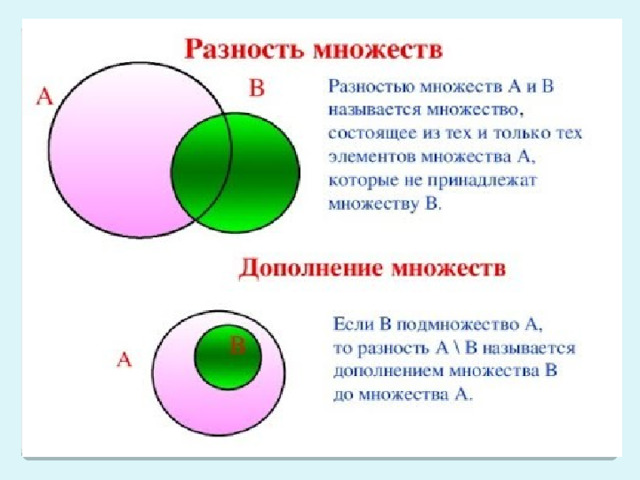
• Вычитание – Разность.
• Операция разность (обозн. \) – при выполнении для множеств А и В, получаем множество С, содержащее элементы А, которые не принадлежат В.
• Вывод.
• Арифметическое действие «Вычитание» схоже с операцией «Разность».
• То есть имеем сходство.
•  
• Сравнение – Надмножества и подмножества.
• Знак ⊂ (Является подмножеством) – для множеств А и В означает: «каждый элемент из   также является элементом из  ».
• Знак ⊃ (Является надмножеством) – для множеств А и В означает: «каждый элемент из   также является элементом из  .
• Вывод.
• Сравнение в арифметике аналогичны знакам «Надмножество» и «Подмножество». То есть сходны.

Операции над множествами

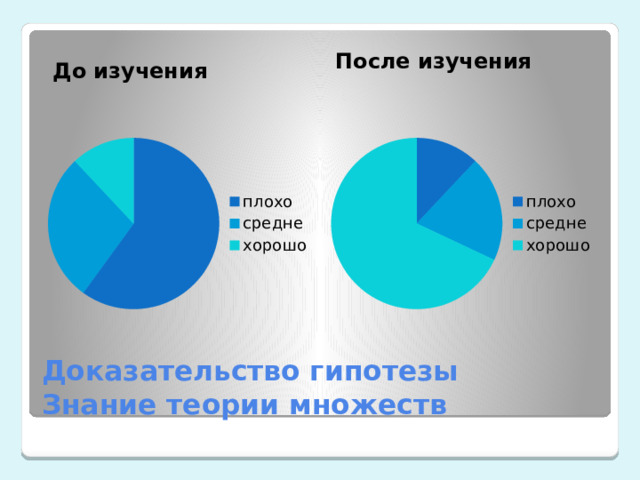
До изучения

После изучения

Доказательство гипотезы Знание теории множеств

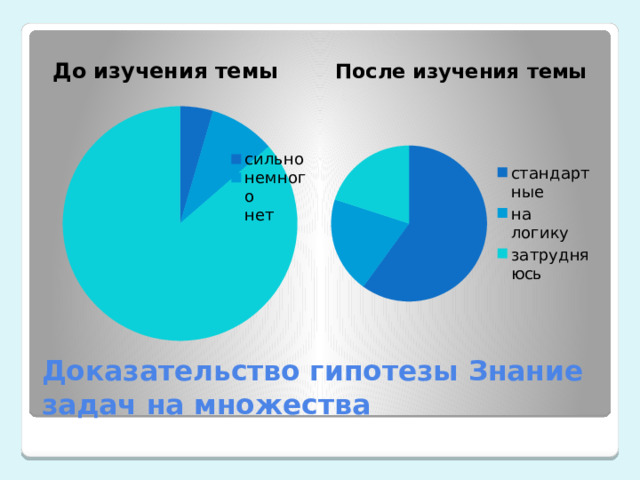
До изучения темы

После изучения темы

Доказательство гипотезы Знание задач на множества

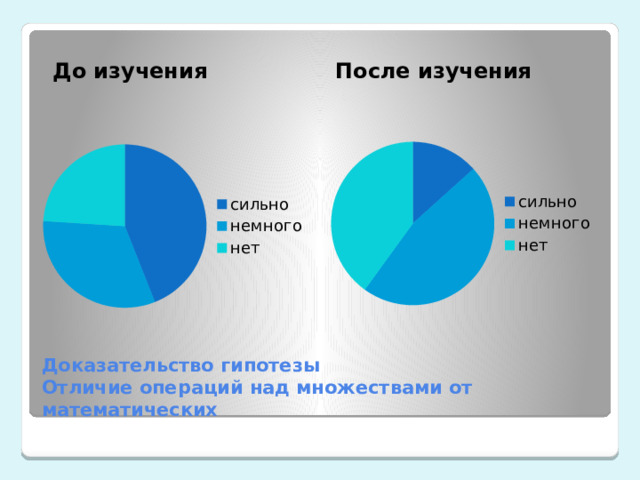
До изучения

После изучения

Доказательство гипотезы Отличие операций над множествами от математических

Заключение

Мы научились определять принадлежность множеств в жизни человека и в науке. Данная тема актуальна и применяется на уроках для решения неравенств, системы неравенств, логических задач использую круги Эйлера, применяется на практике для сравнения или объединения различных показателей.

Представленная работа знакомит с понятием множества с помощью простых примеров из окружающей деятельности. Даны определения операциями для множествами: объединение, пересечение, равные множества, которые наглядно проиллюстрированы диаграммами Эйлера –Венна и рассмотрены на конкретных примерах.

• Из опроса следует, что мои сверстники очень мало знали о множествах. А решение задач с ними вызывали затруднения. Респонденты не могли дать четкое объяснение способу решения..
• Исследования операций показали, решения задач на множества основывается на логике;
• операции над множествами не отличаются от обычных математических операций .

Заключение

• Моя гипотеза подтвердилась полностью. Арифметические действия и операции над множествами сходны и основаны на них.  В процессе работы были рассмотрены следующие вопросы: основные положения теории множеств ( определение множества, конечные и бесконечные множества, обозначения множеств, способы их задания, подмножество); наглядные примеры (помогли мне лучше усвоить понятия). В настоящее время теория множеств является одной из основ различных областей математики ( функциональный анализ, топология, общая алгебра). Ведутся глубокие исследования и в самой теории множеств. Эти исследования связаны с самыми основами математики. Элементами теории множеств могут быть самые разнообразные предметы: виды и подвиды животных, растений; буквы; атомы; числа; функции; точки; углы и т.д. Отсюда с самого начала ясна чрезвычайная широта теории множеств и ее прикладное значение к очень многим областям знаний (математика, биология, физика, экология). Теория множеств является истоком для многих современных наук,. Поэтому так важно усвоить тему «Множества» в школьном курсе. Моя работа может служить учебным пособием на уроках математики, связанных с темой “множества”.

Заключение

• 1. Виленкин Н.Я. Рассказы о множествах. – М.: Наука, 1965.
• 2. Жарковская Н.А. Георг Кантор и теория множеств.
• 3. Корн Г., Корн Т. Справочник по математике. - М.: Наука, 1974.
• 4. Школьная энциклопедия. Математика / Под ред. С.М. Никольского. – М.: Большая российская энциклопедия, 1996.

• 5.https://distant.msu.ru/pluginfile.php/210847/mod_resource/content/1/Лекция%20№1.Множества.pdf
• 6. https://maximumtest.ru/
• 7.https://yandex.ru/video/preview/9966156137097079833?text=множества%206%20класс%20математика&path=yandex_search&parent-reqid=1737015941063941-1763960444186257529-balancer-l7leveler-kubr-yp-vla-176-BAL&from_type=vast
• 8. https://infourok.ru/prezentaciya-po-matematike-na-temu-mnozhestva-operacii-nad-mnozhestvami-6-klass-4575671.html

Литература