"Неравенства, содержащие модуль"

Неравенства, содержащие переменную под знаком модуля

с

• Определение модуля числа.
• Геометрический смысл модуля числа а?
• Геометрический смысл выражения│ х-а │?

Определение модуля

| a | =

Модулем действительного числа а называется само это число, если оно неотрицательное, и противоположное ему число, если данное число отрицательно.

a, если a ≥ 0

-a , если a

Из определения модуля следует:

• | a | ≥0
• | a |= |- a |

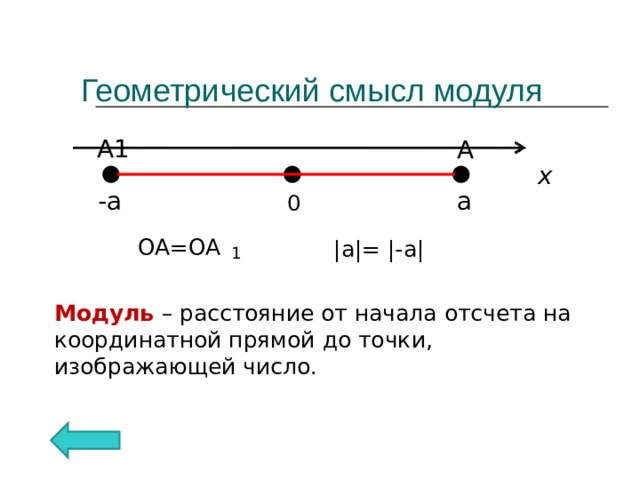
Геометрический смысл модуля

A1

A

x

-a

a

0

OA=O А

| a |= |- a |

1

Модуль – расстояние от начала отсчета на координатной прямой до точки, изображающей число.

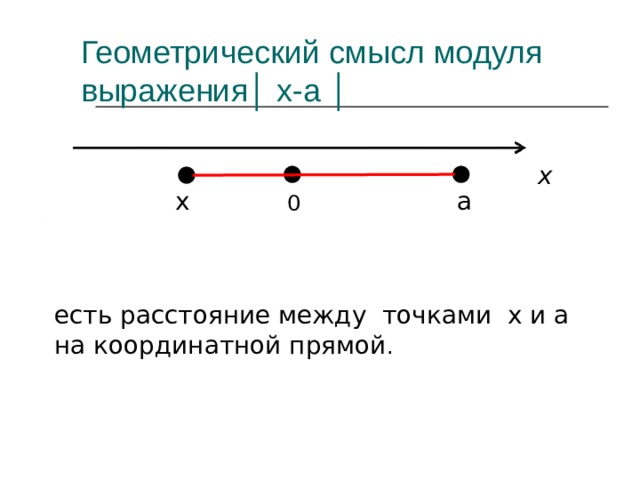
Геометрический смысл модуля выражения│ х-а │

x

х

a

0

есть расстояние между точками x и a на координатной прямой .

Устная работа

• Найдите |3,6|, |0|, |-5|, | √ 7 – 3 |.
• Найдите |3,6|, |0|, |-5|, | √ 7 – 3 |.
• Найдите |3,6|, |0|, |-5|, | √ 7 – 3 |.

• Назовите модуль какого числа равен: 7, 2, 1, 0 ,5 , 6
• Решите уравнения:

• |х|=3 |х|=0 |х|=-3 |х|=х
• |х|=3 |х|=0 |х|=-3 |х|=х
• |х|=3
• |х|=0
• |х|=-3
• |х|=х

Решение уравнений

Решите самостоятельно:

1. |х|= 2,6

х= 2,6 или х=- 2,6

Ответ: -2,6 ; 2,6

2. |х + 5 |= 3

х + 5 = 3 или х + 5 =- 3

• 1. |х|= 2,6 х= 2,6 или х=- 2,6 Ответ: -2,6 ; 2,6 2. |х + 5 |= 3 х + 5 = 3 или х + 5 =- 3
• 1. |х|= 2,6 х= 2,6 или х=- 2,6 Ответ: -2,6 ; 2,6 2. |х + 5 |= 3 х + 5 = 3 или х + 5 =- 3

х= 3-5 х= -3 -5

х= -2 х= -8

Ответ: -8 ; -2

|2х-5|=7

|6-2х|=8

|х+3|=0

|3х+2|= -3

• |2х-5|=7 |6-2х|=8 |х+3|=0 |3х+2|= -3
• |2х-5|=7 |6-2х|=8 |х+3|=0 |3х+2|= -3

Проверка

|2х-5|=7

х=6 ,х=-1

|6-2х|=8

х=-1 х=7

|х+3|=0

х=-3

|3х+2|= -3

Нет решений

• |2х-5|=7 х=6 ,х=-1 |6-2х|=8 х=-1 х=7 |х+3|=0 х=-3 |3х+2|= -3 Нет решений
• |2х-5|=7 х=6 ,х=-1 |6-2х|=8 х=-1 х=7 |х+3|=0 х=-3 |3х+2|= -3 Нет решений

Решение неравенств

|х| ≤ a

Решение:

x

a

-a

- a ≤ х ≤ a

x ͼ [ -a; a ]

Решение неравенств

|х| ≥ a

Решение:

x

a

-a

х ≤ -a ; x ≥ a

x ͼ (- ∞ ; -a ] U [a; + ∞ )

Решение неравенств

|х| ≥ a

|х| ≤ a

Решение:

Решение:

x

x

a

-a

a

-a

- a ≤ х ≤ a

х ≤ -a ; x ≥ a

x ͼ [ -a; a ]

x ͼ (- ∞ ; -a ] U [a; + ∞ )

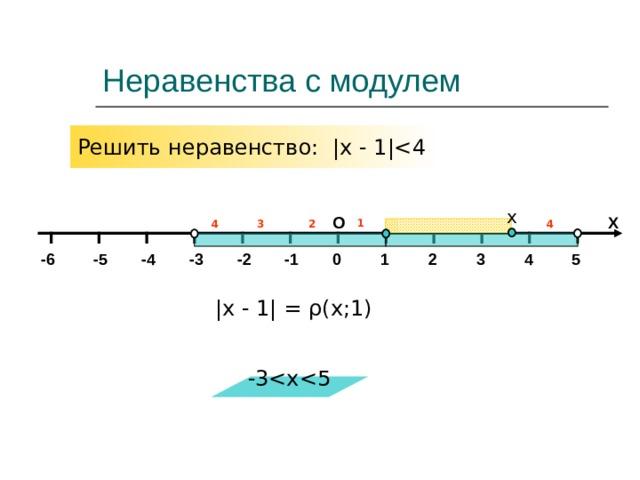
Неравенства с модулем

Решить неравенство: |x - 1 |

х

Х

О

1

4

3

1

4

3

2

2

-2

-6

-5

-4

-3

5

2

3

4

1

0

-1

|x - 1 | = ρ (x; 1 )

-3

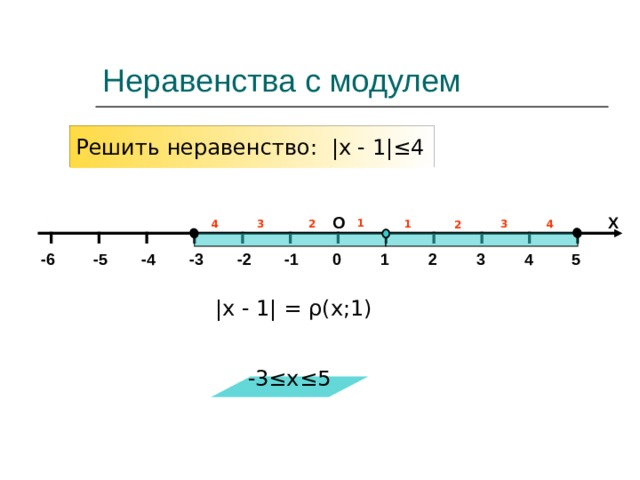
Неравенства с модулем

Решить неравенство: |x - 1 |≤4

Решить неравенство: |x - 1 |

Х

О

1

4

3

1

4

3

2

2

-2

-6

-5

-4

-3

-1

5

2

3

4

1

0

|x - 1 | = ρ (x; 1 )

-3≤x≤5

3 Х О 1 2 1 3 3 2 5 -6 -5 -4 -3 -2 -1 3 4 1 0 2 |x + 2| = ρ (x;-2) x1 Закрь " width="640"

Неравенства с модулем

Решить неравенство: |x + 2 | 3

Х

О

1

2

1

3

3

2

5

-6

-5

-4

-3

-2

-1

3

4

1

0

2

|x + 2| = ρ (x;-2)

x1

Закрь

6 |х-6| |х+5| ≥ 2 |х+1| ≤ 2 " width="640"

Решите неравенства:

• |х|
• |х| 6
• |х-6|
• |х+5| ≥ 2
• |х+1| ≤ 2

2 х+5 2 x2-5 х -3 | 6 х+ 1 | - 2 -3 -1/2 " width="640"

Проверка

• - 7
• х 6
• |х-6|

• Решение:
• Решение:

-5

1

7

• -5

• |х+5| 2

х+5 2

x2-5

х -3

• | 6 х+ 1 |

- 2

-3

-1/2

Дополнительные задания

При каком b верно равенство?

а) | b | =- b

б) | b+ 4 | = b +4

в) | b- 5 | = 5 -b

г) |6- b |

=

1

b-6

1). С какими неравенствами мы познакомились сегодня на уроке?

2). Сколько видов таких неравенств мы сегодня узнали?

3). Всегда ли такие неравенства имеют решения?

4). Как в таком случае мы поступаем?

Д/З

• Теория (выучить теоретические основы : определение модуля, его геометрический смысл, вид изученных неравенств и способы их решения).
• С.49 №206 (1,2)

Урок окончен, молодцы!