Дополнительная общеобразовательная программа "Избранные вопросы математики"

Пояснительная записка

 Направленность образовательной программы. Дополнительная общеобразовательная программа «Избранные вопросы математики» является программой математической направленности. Данная образовательная программа основана на программе факультативного курса по математике для 7 - 9 классов.

 Новизна, актуальность и педагогическая целесообразность данной программы состоит в следующем. Она своим содержанием может привлечь внимание учащихся, которым интересна математика и ее приложения, и которым захочется глубже познакомиться с ее методами и идеями. Предлагаемый курс освещает намеченные, но совершенно не проработанные в общем курсе математики вопросы. На занятиях по данной программе учащиеся будут изучать следующие темы: графики функций, модуль числа, квадратный трехчлен и его приложения. В ходе реализации программы у учащихся, кроме предметных, формируются учебно - познавательные, коммуникативные и информационные компетентности. Кроме того строгая последовательность тем в сочетании с индивидуальным подходом позволять раскрыть творческий потенциал каждого учащегося. Наряду с основной задачей обучения математики – обеспечением прочного и сознательного овладения учащимися системой математических знаний и умений, необходимо каждому современному члену общества, данная программа предусматривает формирование устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, существенным образом связанные с математикой, выбору профиля дальнейшего обучения.

Цели изучения:

 - помочь повысит уровень понимания и практической подготовки в таких вопросах, как:

а) преобразование выражений, содержащих модуль;

б) решение уравнений и неравенств, содержащих модуль;

в) построение графиков функций, содержащих модуль;

 - расширить содержание основного курса, показать нестандартные приемы решения задач на основе квадратного трехчлена; представления о свойствах функции;

 - формировать качества мышления, характерные для математической деятельности и необходимые человеку для жизни в современном обществе.

 Задачи:

 - закрепление основ знаний о функциях и их свойствах;

 - расширение представлений о свойствах функций;

 - формирование умения «читать» графики и называть свойства по формулам;

 - вовлечение учащихся в игровую, коммуникативную, практическую деятельность как фактор личностного развития;

 - научит преобразовывать выражения, содержащие модуль;

 - научить решать уравнения и неравенства, содержащие модуль;

 - углубить знания и умения по теме «Квадратный трехчлен»;

 - помочь учащимся оценивать свой потенциал с точки зрения образовательной перспективы.

 Отличительными особенностями данной дополнительной программы от уже существующих программ является углубление знаний и ее практическая направленность.

 На практике мы часто встречаемся с зависимостями между различными величинами не только в математике, но и в других сферах деятельности. С помощью графиков наиболее естественно отражаются функциональные зависимости одних величин от других.

 Геометрическое преобразование графиков, построение кусочно - заданной функции, графики, содержащие переменную под знаком модуля, позволяют передать красоту математики.

 Начиная с седьмого класса, в центре внимания школьной математики находится понятие функции. Однако размеры школьного учебника, количество часов, выделяемых на изучение темы «Функции» в разных классах, не позволяет показать в сколько - нибудь полном объеме все многообразие задач, требующих для своего решения функционального подхода, научить учащихся глубоко понимать и использовать свойства функции; нет времени изложить историю возникновения этого интересного раздела в школьном курсе математики.

 С другой стороны, авторы контрольно - измерительных материалов ГИА и ЕГЭ уделяют много внимания проверке умения читать по графику свойства функции, использовать их в решении уравнений и неравенств. Поэтому формировать основы этих знаний необходимо начинать как можно раньше.

 Данный курс позволит углубить знания учащихся по истории возникновения понятия, по способам задания функций, по свойствам, а также раскроет перед учащимися новые знания об обратных функциях и свойствах взаимно обратных функций, выходящих за рамки школьной программы.

 Навыки в решении уравнений, неравенств, содержащих модуль и построение графиков элементарных функций, содержащих модуль, необходимы ученику, желающему не только успешно выступить на математических конкурсах и олимпиадах, но и хорошо подготовиться к поступлению и обучения в дальнейшем в высшие учебные заведения. Материал данной программы содержит «нестандартные» методы, которые позволяют более эффективно решать широкий спектр заданий, содержащих модуль.

 Навыки в применении квадратного трехчлена необходимы ученику, желающему хорошо подготовиться для успешной сдачи экзаменов. Познавательный материал данного вопроса будет способствовать не только выработке умений и закреплению навыков, но и формированию устойчивого интереса учащихся к процессу и содержанию деятельности, а также к познавательной и социальной активности.

Тематическое планирование:

Весь материал – смотрите документ.

Муниципальное бюджетное образовательное

учреждение средняя общеобразовательная

школа № 20

Утверждена на заседании

методического совета

протокол № 5 от 11.06.2014 г.

_____________ Н.В. Бауэр

Образовательная программа

дополнительного образования детей

по математике

«Избранные вопросы математики»

Возраст обучающихся – 15-16 лет

Количество детей в группе – 10 человек

Количество часов в год - 31 час

Педагог, реализующий программу –

Дмитриева Ольга Ивановна

Сургут

2014

Пояснительная записка

Направленность образовательной программы. Дополнительная общеобразовательная программа «Избранные вопросы математики» является программой математической направленности. Данная образовательная программа основана на программе факультативного курса по математике для 7-9 классов.

Новизна, актуальность и педагогическая целесообразность данной программы состоит в следующем. Она своим содержанием может привлечь внимание учащихся, которым интересна математика и ее приложения, и которым захочется глубже познакомиться с ее методами и идеями. Предлагаемый курс освещает намеченные, но совершенно не проработанные в общем курсе математики вопросы. На занятиях по данной программе учащиеся будут изучать следующие темы: графики функций, модуль числа, квадратный трехчлен и его приложения. В ходе реализации программы у учащихся, кроме предметных, формируются учебно-познавательные, коммуникативные и информационные компетентности. Кроме того строгая последовательность тем в сочетании с индивидуальным подходом позволять раскрыть творческий потенциал каждого учащегося. Наряду с основной задачей обучения математики – обеспечением прочного и сознательного овладения учащимися системой математических знаний и умений, необходимо каждому современному члену общества, данная программа предусматривает формирование устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, существенным образом связанные с математикой, выбору профиля дальнейшего обучения.

Цели изучения:

- помочь повысит уровень понимания и практической подготовки в таких вопросах, как:

а) преобразование выражений, содержащих модуль;

б) решение уравнений и неравенств, содержащих модуль;

в) построение графиков функций, содержащих модуль;

- расширить содержание основного курса, показать нестандартные приемы решения задач на основе квадратного трехчлена; представления о свойствах функции;

- формировать качества мышления, характерные для математической деятельности и необходимые человеку для жизни в современном обществе.

Задачи:

- закрепление основ знаний о функциях и их свойствах;

- расширение представлений о свойствах функций;

- формирование умения «читать» графики и называть свойства по формулам;

- вовлечение учащихся в игровую, коммуникативную, практическую деятельность как фактор личностного развития;

- научит преобразовывать выражения, содержащие модуль;

- научить решать уравнения и неравенства, содержащие модуль;

- углубить знания и умения по теме «Квадратный трехчлен»;

- помочь учащимся оценивать свой потенциал с точки зрения образовательной перспективы.

Отличительными особенностями данной дополнительной программы от уже существующих программ является углубление знаний и ее практическая направленность.

На практике мы часто встречаемся с зависимостями между различными величинами не только в математике, но и в других сферах деятельности. С помощью графиков наиболее естественно отражаются функциональные зависимости одних величин от других.

Геометрическое преобразование графиков, построение кусочно-заданной функции, графики, содержащие переменную под знаком модуля, позволяют передать красоту математики.

Начиная с седьмого класса, в центре внимания школьной математики находится понятие функции. Однако размеры школьного учебника, количество часов, выделяемых на изучение темы «Функции» в разных классах, не позволяет показать в сколько-нибудь полном объеме все многообразие задач, требующих для своего решения функционального подхода, научить учащихся глубоко понимать и использовать свойства функции; нет времени изложить историю возникновения этого интересного раздела в школьном курсе математики.

С другой стороны, авторы контрольно-измерительных материалов ГИА и ЕГЭ уделяют много внимания проверке умения читать по графику свойства функции, использовать их в решении уравнений и неравенств. Поэтому формировать основы этих знаний необходимо начинать как можно раньше.

Данный курс позволит углубить знания учащихся по истории возникновения понятия, по способам задания функций, по свойствам, а также раскроет перед учащимися новые знания об обратных функциях и свойствах взаимно обратных функций, выходящих за рамки школьной программы.

Навыки в решении уравнений, неравенств, содержащих модуль и построение графиков элементарных функций, содержащих модуль, необходимы ученику, желающему не только успешно выступить на математических конкурсах и олимпиадах, но и хорошо подготовиться к поступлению и обучения в дальнейшем в высшие учебные заведения. Материал данной программы содержит «нестандартные» методы, которые позволяют более эффективно решать широкий спектр заданий, содержащих модуль.

Навыки в применении квадратного трехчлена необходимы ученику, желающему хорошо подготовиться для успешной сдачи экзаменов. Познавательный материал данного вопроса будет способствовать не только выработке умений и закреплению навыков, но и формированию устойчивого интереса учащихся к процессу и содержанию деятельности, а также к познавательной и социальной активности.

Программа предназначена для учащихся 9 классов с любой степенью подготовленности, способствует развитию познавательных интересов, мышления учащихся, представляет возможность подготовиться к сознательному выбору профиля обучения и дальнейшей специализации.

Этапы и условия реализации программы. Данная программа рассчитана на 31 час в год, по 1 часу в неделю, предполагает компактное и четкое изложение теории вопросов, решение типовых задач, самостоятельную работу (или домашнего решения). Все занятия направлены на развитие интереса школьников к предмету, на расширение представлений об изучаемом материале, на решение новых и интересных задач.

Курс характеризуется сочетанием логической строгости и геометрической наглядности. Увеличивается теоретическая значимость изучаемого материала, расширяются его внутренние логические связи, заметно повышается роль дедукции. Учащиеся овладевают приемами аналитико-синтетической деятельности при решении задач.

Программа является открытой, в нее можно добавлять новые фрагменты, развивать тематику или заменять какие-либо разделы другими. Главное, чтобы они были небольшими по объему, интересными для учащихся, соответствовали их возможностям. Программа мобильна, т.е. дает возможность уменьшить количество задач по данной теме при установлении степени достижения результатов.

Основные формы организации учебных занятий: лекция, объяснение, практическая работа, семинар, творческие задания.

Ожидаемые результаты и способы определения их результативности.

Учащиеся должны знать:

- понятие функции как математической модели, описывающих разнообразие реальных зависимостей;

- определение основных свойств функции (область определения, область значений, четность, возрастание, экстремумы, обратимость и т.д.);

- понятие модуля числа;

- формулы корней квадратного чрехчлена.

Учащиеся должны уметь:

- правильно употреблять функциональную терминологию;

- исследовать функцию и строить ее график;

- определять по графику функции ее свойства;

- преобразовывать выражения содержащие модуль;

- решать уравнения и неравенства, содержащие модуль;

- находить корни квадратного трехчлена, выбирая при этом рациональные решения;

- преобразовывать квадратный трехчлен;

- проводить самостоятельные исследования корней квадратного трехчлена.

Формы подведения итогов.

Установление степени достижения учащимися промежуточных и итоговых результатов проводится благодаря использованию практикумов, самостоятельных работ, тестов, консультаций. Контроль знаний и умений учащихся можно определять в виде учета решенных задач, а также плановых самостоятельных и практических работ, тестов.

Формой итоговой аттестации является представление «Портфеля достижений», который включает в себя:

- конспекты занятий;

- схему исследования функций;

- самостоятельные исследования функций (не менее четырех);

- «Применение функций в природе и технике» (информация в любой форме;

- Тесты (не менее двух);

- Анализ собственных успехов (в любой форме).

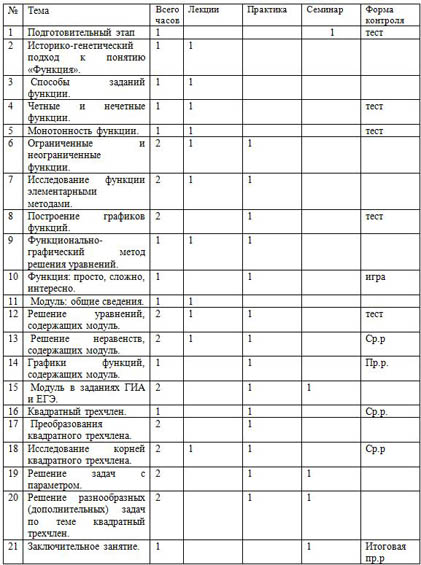
Учебно-тематическое план

дополнительной образовательной программы

Содержание программы

Тема 1. Подготовительный этап.

Функция, область определения, множество значений функции, используемые обозначения, элементарные функции.

Тема 2. Историко-генетический подход к понятию «Функция».

Развитие функциональных зависимостей. Краткое знакомство с работами великих математиков (Декарт, Ферма, Лейбниц, Ньютон, Эйлер и др.)

Тема 3. Способы заданий функции.

Табличный способ задания функции, графическое задание, аналитическое задание функции.

Тема 4. Четные и нечетные функции.

Четная функция. Алгоритм выяснения четности функции. Нечетная функция. Алгоритм выяснения нечетности функции.

Тема 5. Монотонность функции.

Возрастание и убывание функции, свойства монотонности функции, определение монотонности функции, определение промежутков монотонности по графику и по формулам.

Тема 6. Ограниченные и неограниченные функции.

Ограниченность функции, наибольшее и наименьшее значение функции, нахождение множества значений функции.

Тема 7. Исследование функции элементарными методами.

Схема исследования функции. Примеры исследования функций.

Тема 8. Построение графиков функций.

Практическое применение предварительного исследования функций, заданных формулами для наглядного представления их с помощью графиков и более подробное исследование с его помощью.

Тема 9. Функционально-графический метод решения уравнений.

Исследование функций. Практическое применение исследования функции и построение графиков функций при решении уравнений.

Тема 10. Функция: просто, сложно, интересно.

Игра «Восхождение на вершину знаний».

Тема 11. Модуль: общие сведения.

Модуль: общие сведения: определение, свойства модуля, геометрический смысл модуля. Преобразование выражений, содержащих модуль.

Тема 12. Решение уравнений, содержащих модуль.

Решение уравнений вида f|x| = a; |f(x)| = g(x); |f(x)| = |g(x)|.

Тема 13. Решение неравенств, содержащих модуль.

Решение неравенств вида: f|x| a; f|x| a; f|x |g(x); f|x| g(x)|.

Решение уравнений и неравенств, содержащих модуль в модуле. Метод замены переменной. Решение систем уравнений и неравенств, содержащих модуль.

Тема 14. Графики функций, содержащих модуль.

Построение графиков функций, содержащих модуль.

Тема 15. Модуль в заданиях ГИА и ЕГЭ.

Решение заданий ГИА и ЕГЭ, содержащих модуль.

Тема 16. Квадратный трехчлен.

Понятие квадратного трехчлена. Общие сведения. Значение квадратного трехчлена при различных значениях переменной. Корни квадратного трехчлена.

Тема 17. Преобразования квадратного трехчлена.

Составление квадратного трехчлена по его корням. Разложение квадратного трехчлена на линейные множители разными способами.

Тема 18. Исследование корней квадратного трехчлена.

Расположение корней квадратного трехчлена. Примеры применения свойств квадратного трехчлена при решении задач.

Тема 19. Решение задач с параметром.

Квадратный трехчлен и его параметр.

Тема 20. Решение разнообразных (дополнительных) задач по теме квадратный трехчлен.

Решение задач, содержащих параметр более сложного уровня.

Методическое обеспечение

1. Факультативный курс по математике. 7 – 9 класс. Учебное пособие для средней школы. –М.: Просвещение, 2001.

2. Функция в природе и технике. Книга для внеклассного чтения. /Виленкин Н.Я.- М.: Просвещение, 1978.

3. Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. 9 класс/ Л.В. Кузнецова, Е.А. Бунимович и др. – М.: Дрофа,2006

4. Алгебра: Дополнительные главы к школьному учебнику 9 класс.: Макарычев Ю.Н., Миндюк Н.Г. – М.: Просвещение, 2009.

5. Повторяем и систематизируем школьный курс алгебры и начала анализа./В.С. Крамор.- М.: Просвещение, 1992.

6. Повторяем и систематизируем школьный курс геометрии./В.С. Крамор.- М.: Просвещение, 1992.

7. Дидактические материалы по алгебре. 7 класс. Ю.Н. Макарычев, Н.Г. Миндюк и др. – 7 изд. – М.: Просвещение, 2012.

8. Дидактические материалы по алгебре. 9 класс. Ю.Н. Макарычев, Н.Г. Миндюк и др. – 7 изд. – М.: Просвещение, 2012.

9. Задачи с параметрами. 7-11 класс. Практикум. Учебное пособие для средней школы. – ОГУП «Шадринский Дом Печати», 20