Министерство образования и науки Российской Федерации
Министерство образования Иркутской области
Отдел образования администрации города Усолье-Сибирское
Муниципальное бюджетное образовательное учреждение «СОШ №15»
«Избранные вопросы математики»
Авторская педагогическая разработка
(адаптационная, комбинаторная, радикальная)
Автор:
Синькова
Ольга Сергеевна
Учитель математики
МБОУ «СОШ №15»
г.Усолье-Сибирское
2014г.
Министерство образования и науки Российской Федерации
Министерство образования Иркутской области
«Никогда не считай, что ты
знаешь всё, что тебе уже
больше нечему учиться».
Н.Д. Зелинский
Пояснительная записка
Авторская педагогическая разработка «Избранные вопросы математики» составлена на основе Федерального компонента государственного стандарта общего образования. Программа предназначена для учащихся 11 класса и рассчитана на 68 часов. Разработка программы данного курса отвечает как требованиям стандарта математического образования, так и требованиям контрольно-измерительных материалов ЕГЭ базового уровня (части В).
Актуальность авторской педагогической разработки Изучение математики на базовом уровне среднего (полного) общего образования направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
В связи с данными целями возникает основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену общества, достаточных для изучения смежных дисциплин и продолжения образования.
Наряду с решением основной задачи изучения математики программа факультатива предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии, существенным образом связанные с математикой, подготовку к обучению в вузе.
ЕГЭ по математике совмещает два экзамена – выпускной школьный и вступительный в ВУЗ. В связи с этим материал, усвоение которого проверяется при сдаче ЕГЭ, значительно шире материала, проверяемого при сдаче выпускного экзамена. Наряду с вопросами содержания школьного курса алгебры и начал анализа 10-11 классов проверяется усвоение ряда вопросов курсов алгебры 7-9 классов и геометрии 7-11 классов, которые традиционно контролируются на вступительных экзаменах. Таким образом, для подготовки к сдаче ЕГЭ необходимо повторить не только материал курса алгебры и начал анализа, но и некоторых разделов курса математики основной и средней школы: проценты, пропорции, прогрессии, материал курса планиметрии 7-9 классов и курса стереометрии 10-11 классов.
Новизна авторской педагогической разработки В основу авторской педагогической разработки положен обязательный минимум содержания основных образовательных программ. Спецкурс «Избранные вопросы математики», предусматривает возможность изучения содержания курса с различной степенью полноты, обеспечивает прочное и сознательное овладение учащимися системой математических знаний и умений, достаточных для изучения сложных дисциплин и продолжения образования в высших учебных заведениях.
Программа предусматривает системный подход к изучению математики. Она включает полностью содержание курса математики общеобразовательной школы, ряд дополнительных вопросов, непосредственно примыкающих к этому курсу, расширяющих и углубляющих его по основным идейным линиям, а также включены самостоятельные разделы. Такой подход определяет следующие тенденции:
Создание в совокупности с основными разделами курса для удовлетворения интересов и развития способностей учащихся.
Восполнение содержательных пробелов основного курса, придающее содержанию расширенного изучения необходимую целостность.
Цели курса:
- практическая помощь учащимся в подготовке к Единому государственному экзамену по математике через повторение, систематизацию, расширение и углубление знаний;
- создание условий для дифференциации и индивидуализации обучения, выбора учащимися разных категорий индивидуальных образовательных траекторий в соответствии с их способностями, склонностями и потребностями;
- интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем.
Задачи курса:
- подготовить к успешной сдаче ЕГЭ по математике на базовом уровне;
- активизировать познавательную деятельность учащихся;
- расширить знания и умения в решении различных математических задач, подробно рассмотрев возможные или более приемлемые методы их решения;
- формировать общие умения и навыки по решению задач: анализ содержания, поиск способа решения, составление и осуществление плана, проверка и анализ решения, исследование;
- привить учащимся основы экономической грамотности;
- повышать информационную и коммуникативную компетентность учащихся;
- помочь ученику оценить свой потенциал с точки зрения образовательной перспективы.
После изучения курса обучающиеся должны знать и уметь:
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира;
знать широту применения процентных вычислений в жизни, решать основные задачи на проценты, применять формулу сложных процентов;
решать различные типы текстовых задач с практическим содержанием на проценты, движение, работу, концентрацию, смеси, сплавы, десятичную запись числа, на использование арифметической и геометрической прогрессии;
решать планиметрические задачи, связанные с нахождением площадей, линейных или угловых величин треугольников или четырехугольников;
проводить тождественные преобразования иррациональных, показательных, логарифмических и тригонометрических выражений;
решать иррациональные, логарифмические и тригонометрические уравнения и неравенства;
решать системы уравнений изученными методами.
строить графики элементарных функций и проводить преобразования графиков, используя изученные методы;
Понимать и уметь использовать физический и геометрический смысл производной
применять аппарат математического анализа к решению задач;
решать стереометрические задачи, содержащие разный уровень необходимых для решения обоснований и количество шагов в решении задач, включенных в часть I
применять основные методы геометрии (проектирования, преобразований, векторный, координатный) к решению геометрических задач.
В процессе изучения материала используются как традиционные формы обучения, так и самообразование, саморазвитие учащихся посредством самостоятельной работы с информационным и методическим материалом, интернет – ресурсами.
Предполагаются следующие формы организации обучения:
индивидуальная, групповая, коллективная, беседа, практикум, консультация;
взаимное обучение, самообучение, саморазвитие.
Эффективность обучения отслеживается следующими формами контроля:
выполнение тестовых заданий по каждой теме факультатива, два из которых – итоговые.
Показателем эффективности обучения следует считать повышающийся интерес к математике, творческую активность учащихся, успешная сдача ЕГЭ по математики.
Итоговый контроль предусматривает:
Выполнение демоверсии ЕГЭ по математики.
Содержание курса:
Простейшие текстовые задачи – 10ч
Округление с недостатком. Проценты, округление
Чтение графиков и диаграмм - 2ч
Определение величины по графику и диаграмме
Задачи на выбор оптимального варианта -
Выбор варианта из нескольких возможных
Планиметрия: вычисления длин и площадей – 4ч
Треугольники, четырехугольники. Координатная плоскость. Задачи на квадратной решетке. Векторы. Вписанная и описанная окружность.
Начала теории вероятности – 3 ч
Классическое определение вероятности. Теоремы о вероятностных событий.
Простейшие уравнения –7ч
Линейные, квадратные, кубические уравнения. Рациональные уравнения. Иррациональные уравнения. Показательные уравнения. Логарифмические уравнения. Тригонометрические уравнения.
Планиметрия: задачи связанные с углами – 4ч
Треугольники, четырехугольники. Окружность вписанная и описанная.
Производная и первообразная – 6ч
Физический смысл производной. Геометрический смысл производной. Применение производной к исследованию функций. Первообразная.
Стереометрия – 3ч
Углы и расстояния. Сечения многогранников плоскостью.
Вычисления и преобразования- 3ч
Тождественные преобразования иррациональных и степенных выражений. Тождественные преобразования логарифмических выражений. Преобразования тригонометрических выражений.
Задачи с прикладным содержанием- 5ч
Линейные уравнения, квадратичные уравнения и степенные уравнения и неравенства. Рациональные и иррациональные уравнения и неравенства. Показательные и логарифмические уравнения и неравенства. Тригонометрические уравнения и неравенства.
Задачи по стереометрии – 4ч
Площади поверхностей и объемы тел.
Текстовые задачи – 6 ч
Задачи на проценты, сплавы и смеси. Задачи на движение по воде. Задачи на совместную работу. Задачи на прогрессии. Решение текстовых задач.
Наибольшее и наименьшее значение функции – 5ч
Исследование простых, иррациональных и иррациональных функций. Исследование произведений и частных. Исследование показательных и логарифмических функций. Исследование тригонометрических функций
Структура и содержание контрольно - измерительных материалов Единого государственного экзамена по математике (3ч.)
Демонстрационный вариант КИМ ЕГЭ. Система оценивания. Примеры заданий с кратким ответом (задания В1-В15). Тренировочные варианты. Компьютерное тестирование: Решу ЕГЭ. Проверь свои знания!
Календарно-тематическое планирование курса
2 часа в неделю, всего 68 часов
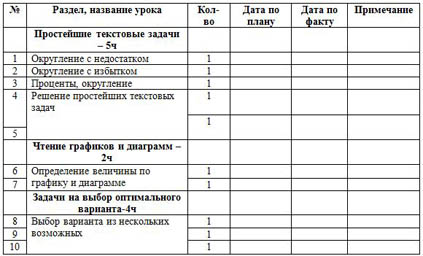
| № | Раздел, название урока | Кол-во | Дата по плану | Дата по факту | Примечание |
|
| Простейшие текстовые задачи – 5ч |
|
|
|
|
| 1 | Округление с недостатком | 1 |
|
|
|
| 2 | Округление с избытком | 1 |
|
|
|
| 3 | Проценты, округление | 1 |
|
|
|
| 4 | Решение простейших текстовых задач | 1 |
|
|
|
| 1 |
|
|
|
| 5 |
|
| Чтение графиков и диаграмм – 2ч |
|
|
|
|
| 6 | Определение величины по графику и диаграмме | 1 |
|
|
|
| 7 | 1 |
|
|
|
|
| Задачи на выбор оптимального варианта-4ч |
|
|
|
|
| 8 | Выбор варианта из нескольких возможных | 1 |
|
|
|
| 9 | 1 |
|
|
|
| 10 | 1 |
|
|
|
| 11 | Решение задач на выбор оптимального варианта | 1 |
|
|
|
|
| Планиметрия: вычисления длин и площадей – 4ч |
|
|
|
|
| 12 | Треугольники, четырехугольники. Координатная плоскость | 1 |
|
|
|
| 13 | Задачи на квадратной решетке. Векторы | 1 |
|
|
|
| 14 | Вписанная и описанная окружность | 1 |
|
|
|
| 15 | Решение задач | 1 |
|
|
|
|
| Начала теории вероятности – 3 ч |
|
|
|
|
| 16 | Классическое определение вероятности | 1 |
|
|
|
| 17 | Теоремы о вероятностных событий | 1 |
|
|
|
| 18 | Решение задач | 1 |
|
|
|
|
| Простейшие уравнения –7ч |
|
|
|
|
| 19 | Линейные, квадратные, кубические уравнения | 1 |
|
|
|
| 20 | Рациональные уравнения | 1 |
|
|
|
| 21 | Иррациональные уравнения | 1 |
|
|
|
| 22 | Показательные уравнения | 1 |
|
|
|
| 23 | Логарифмические уравнения | 1 |
|
|
|
| 24 | Тригонометрические уравнения | 1 |
|
|
|
| 25 | Решение уравнений | 1 |
|
|
|
|
| Планиметрия: задачи связанные с углами – 4ч |
|
|
|
|
| 26 | Треугольники, четырехугольники | 1 |
|
|
|
| 27 | 1 |
|
|
|
| 28 | Окружность вписанная и описанная | 1 |
|
|
|
| 29 | Решение задач | 1 |
|
|
|
|
| Производная и первообразная – 6ч |
|
|
|
|
| 30 | Физический смысл производной | 1 |
|
|
|
| 31 | Геометрический смысл производной | 1 |
|
|
|
| 32 | Применение производной к исследованию функций | 1 |
|
|
|
| 33 | 1 |
|
|
|
| 34 | Первообразная | 1 |
|
|
|
| 35 | Решение задач на производную и первообразную | 1 |
|
|
|
|
| Стереометрия – 4ч |
|
|
|
|
| 36 | Углы и расстояния. Сечения многогранников плоскостью | 1 |
|
|
|
| 37 | 1 |
|
|
|
| 38 | Решение задач | 1 |
|
|
|
| 39 | 1 |
|
|
|
|
| Вычисления и преобразования- 3ч |
|
|
|
|
| 40 | Тождественные преобразования иррациональных и степенных выражений | 1 |
|
|
|
| 41 | Тождественные преобразования логарифмических выражений | 1 |
|
|
|
| 42 | Преобразования тригонометрических выражений | 1 |
|
|
|
|
| Задачи с прикладным содержанием- 5ч |
|
|
|
|
| 43
| Линейные уравнения, квадратичные уравнения и степенные уравнения и неравенства | 1 |
|
|
|
| 44 | Рациональные и иррациональные уравнения и неравенства | 1 |
|
|
|
| 45 | Показательные и логарифмические уравнения и неравенства | 1 |
|
|
|
| 46 | Тригонометрические уравнения и неравенства | 1 |
|
|
|
| 47 | Решение задач с прикладным содержанием | 1 |
|
|
|
|
| Задачи по стереометрии – 4ч |
|
|
|
|
| 48-50 | Площади поверхностей и объемы тел | 3 |
|
|
|
|
|
|
|
|
|
|
|
| 51 | Решение задач по стереометрии | 1 |
|
|
|
|
| Текстовые задачи – 6 ч |
|
|
|
|
| 52 | Задачи на проценты, сплавы и смеси | 1 |
|
|
|
| 53 | 1 |
|
|
|
| 54 | Задачи на движение по воде | 1 |
|
|
|
| 55 | Задачи на совместную работу | 1 |
|
|
|
| 56 | Задачи на прогрессии | 1 |
|
|
|
| 57 | Решение текстовых задач | 1 |
|
|
|
|
| Наибольшее и наименьшее значение функции – 5ч |
|
|
|
|
| 58 | Исследование простых, иррациональных и иррациональных функций | 1 |
|
|
|
| 59 | Исследование произведений и частных | 1 |
|
|
|
| 60 | Исследование показательных и логарифмических функций | 1 |
|
|
|
| 61 | Исследование тригонометрических функций | 1 |
|
|
|
| 62 | Исследование функций | 1 |
|
|
|
| 63-65 | Структура и содержание контрольно – измерительных материалов Единого государственного экзамена по математике | 3 |
|
|
|
|
|
|
|
|
|
|
|
| 66-68 | Тренировочное тестирование | 3 |
|
|
|
|
|
|
|
|
|
|
|
Литература
Электронные ресурсы: www.fipi.ru, свободный доступ;
Электронные ресурсы: www.ege.edu.ru, свободный доступ;
Электронные ресурсы: http://reshuege.ru/, свободный доступ;
ЕГЭ-2013. Математика: типовые экзаменационные варианты: 10 вариантов / Под ред. А.Л. Семенова, И.В. Ященко. — М.: Издательство «Национальное образование», 2012. — (ЕГЭ-2013. ФИПИ-школе)
ЕГЭ-2013. Математика: типовые экзаменационные варианты: 30 вариантов / Под ред. А.Л. Семенова, И.В. Ященко. — М.: Издательство «Национальное образование», 2012. — (ЕГЭ-2013. ФИПИ-школе)
ЕГЭ-2013. Математика: актив-тренинг: решение заданий В, С / Под ред. А.Л. Семенова, И.В. Ященко. — М.: Издательство «Национальное образование», 2012. — (ЕГЭ-2013. ФИПИ-школе)
ЕГЭ-2013. Математика: тематический сборник заданий / Под ред. А.Л. Семенова, И.В. Ященко. — М.: Издательство «Национальное образование», 2012. — (ЕГЭ-2013. ФИПИ-школе)
ЕГЭ-2013: Математика / ФИПИ авторы-составители: Ященко И.В., Семенов А.Л., Высоцкий И.Р., Гущин Д.Д., Захаров П.И., Панферов В.С., Посицельский С.Е., Семенов А.В., Семенова М.А., Сергеев И.Н., Смирнов В.А., Шестаков С.А., Шноль Д.Э.– М.: Астрель, 2012.
Отличник ЕГЭ. Математика. Решение сложных задач / ФИПИ авторы- составители: Панферов В.С., Сергеев И.Н. – М.: Интеллект-Центр, 2012.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Авторская педагогическая разработка факультативного курса по математике «Избранные вопросы математики» (40.75 КB)
Авторская педагогическая разработка факультативного курса по математике «Избранные вопросы математики» (40.75 КB)
 0
0 821
821 111
111 Нравится
0
Нравится
0


