Элективный курс « Модуль в школьном курсе математики»
Пояснительная записка
Элективный курс предназначен для учащихся 9 классов, проявляющих повышенный к математике. Данный курс направлен на расширение и углубление знаний учащихся, повышение уровня математической подготовки через решение большого класса задач, содержащих понятие модуля. Навыки в решении уравнений, неравенств, содержащих модуль, и построение графиков элементарных функций, необходимы любому ученику, желающему успешно подготовиться к сдаче ОГЭ по математике. В методической литературе «модулю» уделяется немало внимания, однако практика показывает, что задания с модулем вызывают у учащихся затруднения, и они допускают ошибки. Одна из причин таких ошибок кроется, в непонимании учащимися определения модуля числа. Материал данного курса содержит «нестандартные» методы, которые позволяют более эффективно решать широкий класс заданий, содержащих модуль, и может использоваться учителем как на уроках математики в 9 классах, так и на факультативных занятиях. Наряду с основной задачей обучения математики – обеспечением прочного и сознательного овладения учащимися системой математических знаний и умений, данный курс предусматривает формирование устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, существенным образом связанные с математикой, выбору профиля дальнейшего обучения.
Программа курса рассчитана на 17 учебных часов.
Цели курса:
Помочь обучающимся повысить уровень понимания и практической подготовки в таких вопросах, как: а) преобразование выражений, содержащих модуль; б) решение уравнений и неравенств, содержащих модуль; в) построение графиков элементарных функций, содержащих модуль.
Задачи курса:
научить обучающихся преобразовывать выражения, содержащие модуль;
научить обучающихся решать уравнения и неравенства, содержащие модуль;
научить обучающихся строить графики, содержащие модуль;
помочь ученикам выявить свой потенциал с точки зрения дальнейшей образовательной перспективы.
В результате изучения курса учащиеся должны знать и уметь:
должны знать определение модуля числа и его геометрическую интерпретацию.
уметь решать простейшие уравнения и неравенства с модулем.
уметь строить графики функций с модулем.
уметь выполнять алгебраические преобразования с модулем числа.
Для успешного анализа и самоанализа необходимо определить критерии оценки деятельности учащихся. Хотя курс может вестись и по безоценочной системе.
Возможные критерии оценок.
Критерии при выставлении оценок могут быть следующие.
Оценка «отлично» – обучающийся освоил теоретический материал курса, получил навыки в его применении при решении конкретных задач; в работе над индивидуальными заданиями учащийся демонстрирует умение работать самостоятельно, творчески. Как правило, для получения высокой оценки обучающийся должен показать не только знание теории и владение набором стандартных методов, но и нестандартность мышления, высокую математическую культуру.
Оценка «хорошо» – обучающийся освоил идеи и методы данного курса в такой степени, что может справиться со стандартными заданиями; наблюдаются определенные положительные результаты, свидетельствующие об интеллектуальном росте и о возрастании общих умений обучающегося. Оценка «удовлетворительно» – обучающийся освоил наиболее простые идеи и методы курса, что позволяет ему достаточно успешно выполнять простые задания.
Содержание программы
Тема 1 Определение модуля и его свойства. (1 ч)
Занятие 1. Общие сведения: определение, свойства модуля, геометрический смысл модуля.
М е т о д ы о б у ч е н и я: лекция, выполнение тренировочных упражнений.
Ф о р м ы к о н т р о л я: кратковременная самостоятельная работа.
Занятие 2. Преобразование выражений, содержащих модуль (1 ч)
М е т о д ы о б у ч е н и я: лекция, выполнение тренировочных упражнений.
Ф о р м ы к о н т р о л я: кратковременная самостоятельная работа
Тема 2. Решение уравнений, содержащих модуль (4 ч)
Занятие 3. Решение уравнений, содержащих модуль (1 ч). Решение уравнений вида:
| |х| = а, |х – b| = а, |f(х)| = а |
|
М е т о д ы о б у ч е н и я: лекция, выполнение тренировочных упражнений.
Ф о р м ы к о н т р о л я: кратковременная самостоятельная работа
Занятие 4. Геометрическая интерпретация уравнений вида:
|х – а| – |х – b| = с.
М е т о д ы о б у ч е н и я: лекция, выполнение тренировочных упражнений.
Ф о р м ы к о н т р о л я: кратковременная самостоятельная работа
Занятие 5. Решение уравнений, содержащих модуль (1 ч). Решение уравнений вида:
|f(х)| = g(х); |f(х)| = |g(х)|
М е т о д ы о б у ч е н и я: лекция, выполнение тренировочных упражнений.
Ф о р м ы к о н т р о л я: кратковременная самостоятельная работа
Занятие 6. Проверочная работа (1ч)
Тема 3. Решение неравенств, содержащих модуль (5 ч)
Занятие 7. Решение неравенств, содержащих модуль (1 ч). Решение неравенств вида: |f(х)| ≤ а ; f|х| а
М е т о д ы о б у ч е н и я: лекция, выполнение тренировочных упражнений.
Ф о р м ы к о н т р о л я: кратковременная самостоятельная работа
Занятие 8-9. Решение неравенств, содержащих модуль (2 ч). Решение неравенств вида:
|f(х)| ≤ |g(х)| ; |f(х)| ≤ g(х) ; |f(х)| g(х)
М е т о д ы о б у ч е н и я: лекция, выполнение тренировочных упражнений.
Ф о р м ы к о н т р о л я: кратковременная самостоятельная работа
Занятие 10. Решение уравнений и неравенств, содержащих модуль. Семинар (1 ч)
Решение уравнений и неравенств, содержащих модуль в модуле. Метод замены переменной.
М е т о д ы о б у ч е н и я: Семинар
Занятие 11. Проверочная работа (1ч)
Тема 4. Графики функций, содержащих модуль (6 ч)
Занятие 12-13. Построение графиков функций, содержащих модуль (2 ч). Построение графиков функций вида:
у =|f(x)| и у = f(|x|)
М е т о д ы о б у ч е н и я: лекция, выполнение тренировочных упражнений.
Ф о р м ы к о н т р о л я: кратковременная самостоятельная работа
Занятие 14-15. Построение графиков функций, содержащих модуль (2 ч). Построение графиков уравнений вида:
|у| = f(х) и |у| = |f(х)|.
М е т о д ы о б у ч е н и я: лекция, выполнение тренировочных упражнений.
Ф о р м ы к о н т р о л я: кратковременная самостоятельная работа.
Занятие 16. Построение квадратичных функций, содержащих модули.
М е т о д ы о б у ч е н и я: лекция, выполнение тренировочных упражнений.
Ф о р м ы к о н т р о л я: кратковременная самостоятельная работа.
Занятие 17. Итоговая проверочная работа (1 ч).
Приложение
Определение. Модулем неотрицательного действительного числа а называют само это число:
| а| = а; модулем отрицательного действительного числа а называют противоположное число:
I а| = - а.
Короче это записывают так: 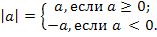
Например, |6| = 6, |-3| = 3, |-10,45| = 10,45.
Свойства модуля
1) Модули противоположных чисел равны |a|=|–a|.
2) Квадрат модуля числа равен квадрату этого числа |a|2 = a2.
3) Квадратный корень из квадрата числа есть модуль этого числа 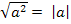
4) Модуль числа есть число неотрицательное |a|≥ 0.
5) Постоянный положительный множитель можно выносить за знак модуля |сa|= с|a|, с 0.
6) Если |a| = |b|, то a = ± b.
7) Модуль произведения двух (и более) чисел равен произведению их модулей |a ∙ b| = |a| ∙ |b|.
Геометрический смысл модуля
Модуль числа — это расстояние от нуля до данного числа а.
Например, |-5| = 5. То есть расстояние от точки -5 до нуля равно 5.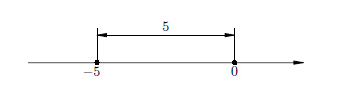
ЛИТЕРАТУРА.
1. Алимов Ш. А. Алгебра: Учебник для 7 класса средней школы. – М.: Просвещение, 2011;
2. Алимов Ш. А. Алгебра: Учебник для 8 класса средней школы. – М.: Просвещение, 2011;
3. Алимов Ш. А. Алгебра: Учебник для 9 класса средней школы. – М.: Просвещение, 2011;
4. Боревский Л. Я. Рациональные уравнения с модулем. | Математика “ 1 сентября” – 2001. - № 32;
5. Голубев В. И. Школа решения нестандартных задач. | Математика “ 1 сентября” – 2005. - № 5;
6. Дорофеев Г. В. Математика 6 класс: Учебник для общеобразовательных учреждений. – М.: Дрофа, 1998;
7. Ильина С. Д. Графическое решение уравнений, содержащих знак модуля. | Математика в школе. – 2001. - № 8.
8. Кострикина Н. П. Задачи повышенной трудности в курсе алгебры 7 – 9 классов. – М.: Просвещение, 1991
9. Крамор В. С. Повторяем и систематизируем школьный курс алгебры и начал анализа. – М.: Просвещение, 1990;
10. Кривоногов В. В. Нестандартные задачи по математике 5 – 11 класс. – Волгоград: Учитель, 2003;
11. Лаврентьева О. Изучаем тему “модуль числа” 8 класс. | Математика “1 сентября” – 1996. - № 12.
12. Садыкина Н. Построение графиков функций и зависимостей, содержащих знак модуля. | Математика “1 сентября”. – 2004. - № 33;
13. Скворцова М. Уравнения и неравенства с модулем 8 – 9 класс. | Математика “1 сентября”. – 2004. - № 20;
14. Шестаков С. Геометрический смысл модуля и его применение к решению уравнений и неравенств. | Математика “1 сентября”. – 2004. - № 44;
15. Шуба М. Э. Занимательные задания в обучении математике. – М.: Просвещение, 1995.


 Получите свидетельство
Получите свидетельство Вход
Вход












 Элективный курс «Модуль в школьном курсе математики» (32.88 КB)
Элективный курс «Модуль в школьном курсе математики» (32.88 КB)
 0
0 1931
1931 161
161 Нравится
0
Нравится
0


