"Задачи на построение сечений"

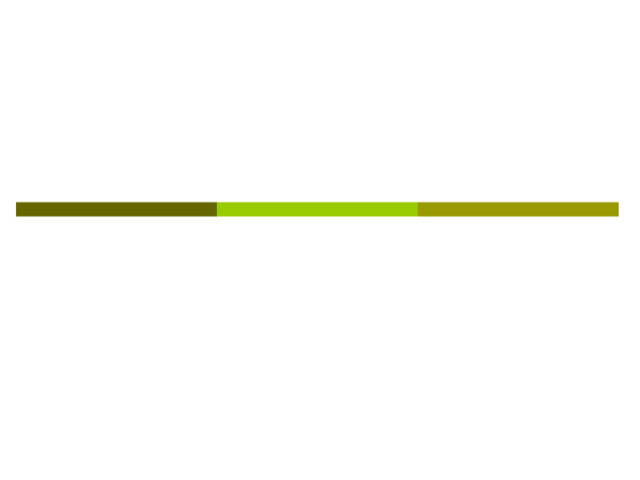
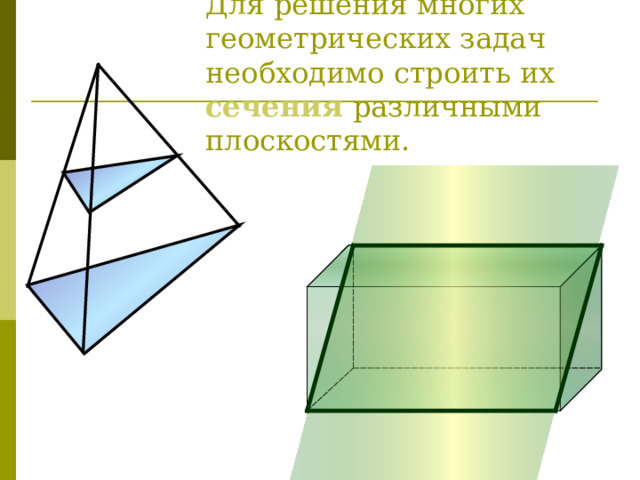
Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.

1.Секущая плоскость тетраэдра(параллепипеда)-это любая плоскость, по обе стороны от которой имеются точки данного тетраэдра (параллепипеда).

2.Многоугольник, сторонами которого являются отрезки, пересекающие грани тетраэдра (параллепипеда) называется сечением тетраэдра (параллепипеда).

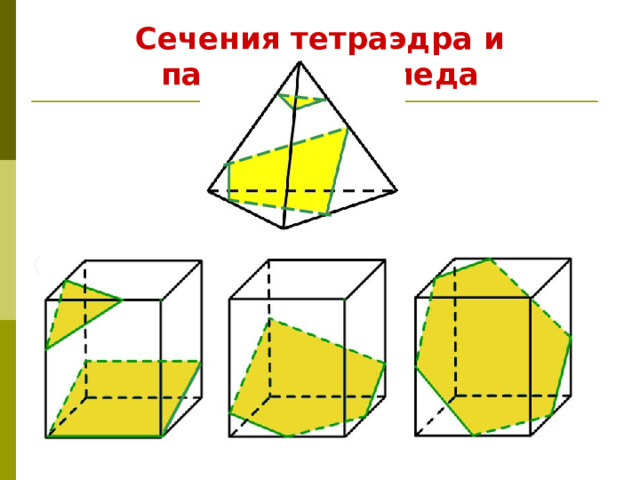
Сечения тетраэдра и параллелепипеда

Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками.

При этом необходимо учитывать следующее:

1. Соединять можно только две точки, лежащие

в плоскости одной грани.

2. Секущая плоскость пересекает параллельные грани по параллельным отрезкам.

3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.

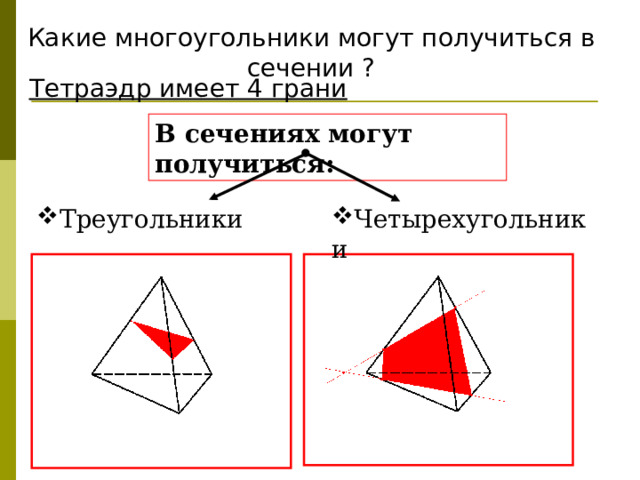
Какие многоугольники могут получиться в сечении ?

Тетраэдр имеет 4 грани

В сечениях могут получиться:

• Четырехугольники

• Треугольники

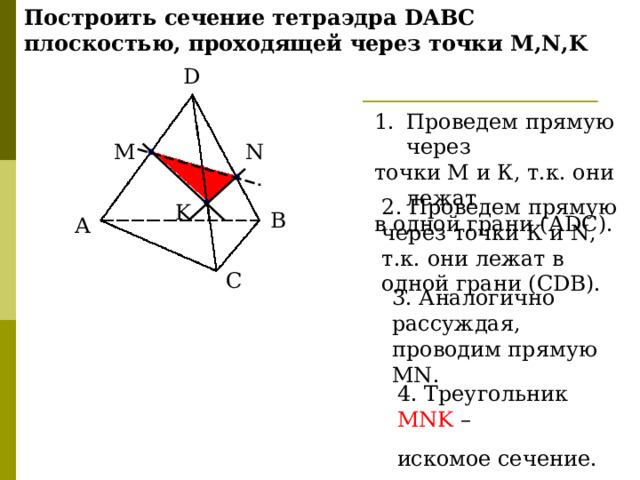
Построить сечение тетраэдра DABC плоскостью, проходящей через точки M , N , K

D

D

• Проведем прямую через

точки М и К, т.к. они лежат

в одной грани (А DC ).

N

M

2. Проведем прямую через точки К и N , т.к. они лежат в одной грани (С DB ).

K

B

A

B

A

C

C

3. Аналогично рассуждая, проводим прямую MN .

4. Треугольник MNK –

искомое сечение.

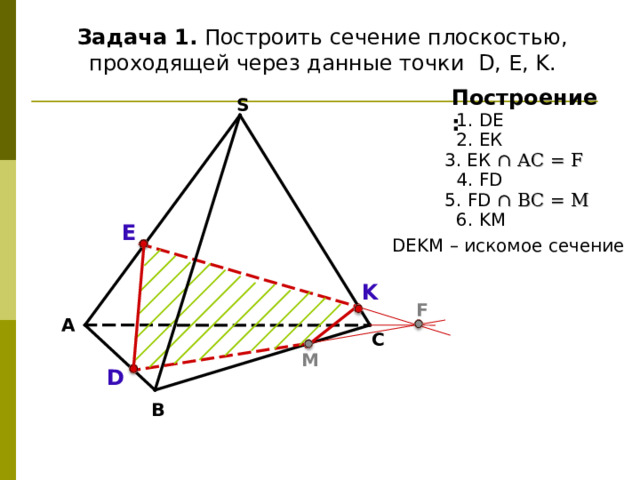
Задача 1. Построить сечение плоскостью, проходящей через данные точки D, Е, K .

Построение:

S

1 . DE

2. ЕК

3. ЕК ∩ АС = F

4 . FD

5. FD ∩ B С = M

6 . KM

E

D Е K М – искомое сечение

K

F

А

С

M

D

В

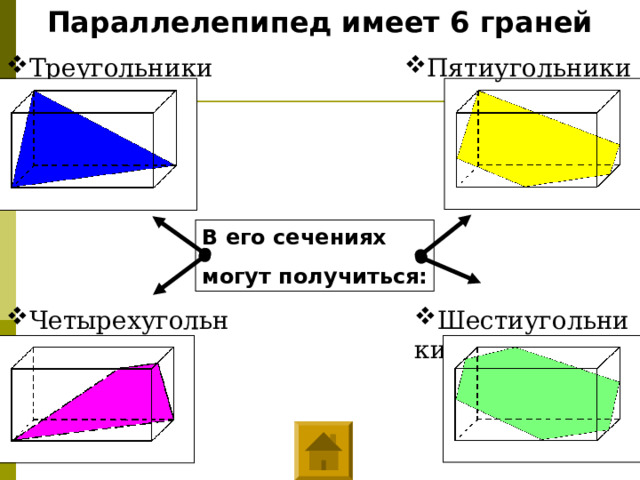
Параллелепипед имеет 6 граней

• Треугольники

• Пятиугольники

В его сечениях

могут получиться:

• Четырехугольники

• Шестиугольники

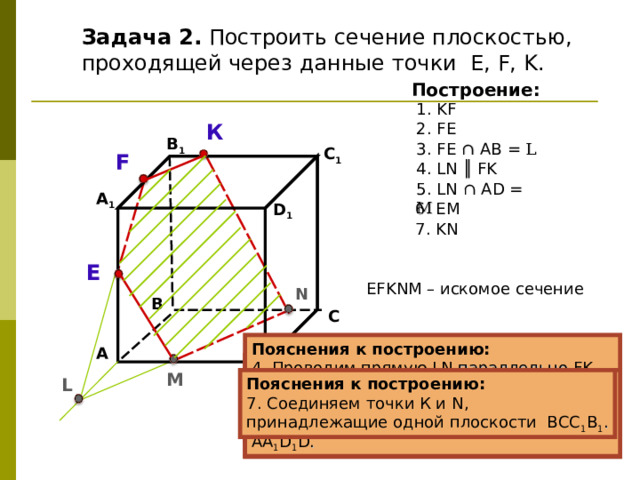
Задача 2. Построить сечение плоскостью, проходящей через данные точки Е, F, K .

Построение:

1. KF

2. FE

К

В 1

3. FE ∩ А B = L

C 1

F

4 . LN ║ FK

5 . LN ∩ AD = M

А 1

6 . EM

D 1

7 . KN

E

EFKNM – искомое сечение

N

В

С

Пояснения к построению:

4 . Проводим прямую LN параллельно FK (если секущая плоскость пересекает противоположные грани, то она пересекает их по параллельным отрезкам).

А

Пояснения к построению:

3. Прямые FE и АВ, лежащие в одной плоскости АА 1 В 1 В, пересекаются в точке L .

Пояснения к построению:

2. Соединяем точки F и E , принадлежащие одной плоскости АА 1 В 1 В.

Пояснения к построению:

1. Соединяем точки K и F , принадлежащие одной плоскости А 1 В 1 С 1 D 1 .

М

D

L

Пояснения к построению:

6 . Соединяем точки Е и М, принадлежащие одной плоскости АА 1 D 1 D .

Пояснения к построению:

7 . Соединяем точки К и N , принадлежащие одной плоскости ВСС 1 В 1 .

Пояснения к построению:

5 . Прямая LN пересекает ребро AD в точке M .

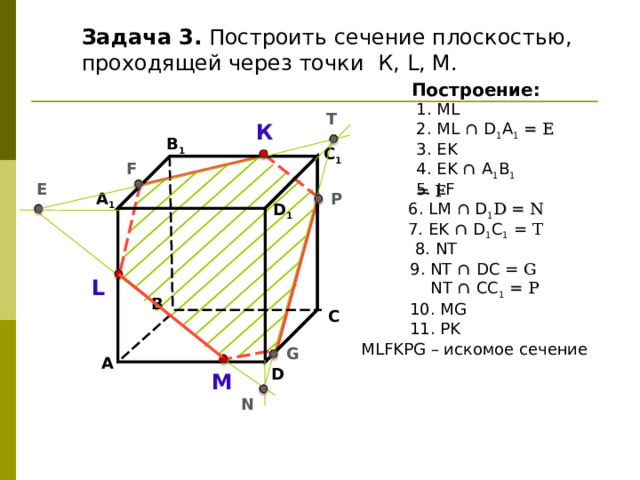
Задача 3. Построить сечение плоскостью, проходящей через точки К, L, М.

Построение:

1. ML

T

2. ML ∩ D 1 А 1 = E

К

В 1

3. EK

C 1

4 . EK ∩ А 1 B 1 = F

F

5 . LF

E

P

А 1

6 . LM ∩ D 1 D = N

D 1

7 . Е K ∩ D 1 C 1 = T

8 . NT

9 . NT ∩ DC = G

NT ∩ CC 1 = P

L

В

10 . MG

С

11 . PK

М LFKPG – искомое сечение

G

А

D

М

N

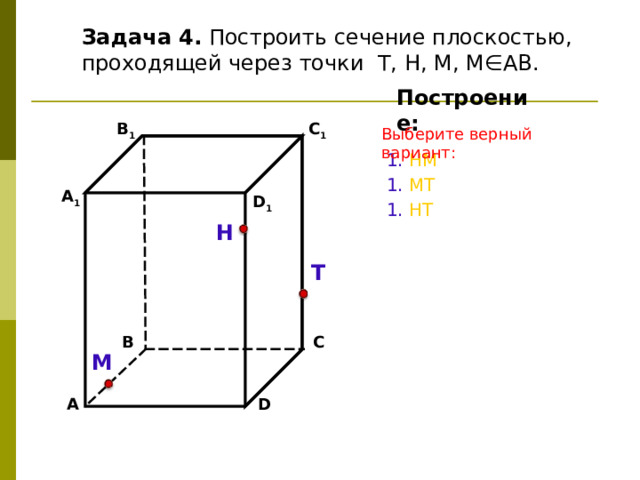
Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ.

Построение:

C 1

В 1

Выберите верный вариант:

1. НМ

1. МТ

А 1

D 1

1. Н T

Н

Т

С

В

М

А

D

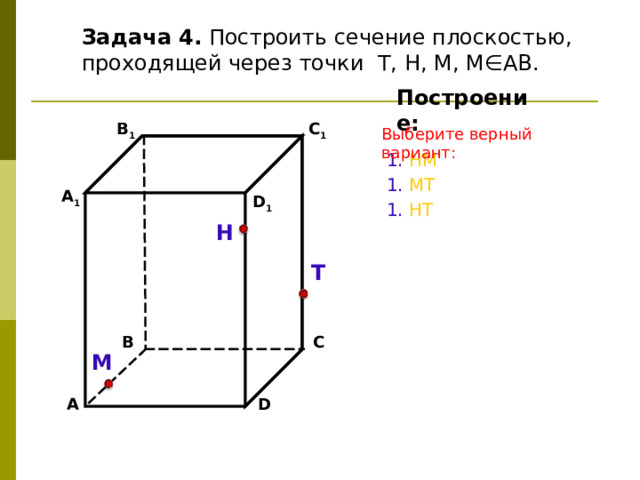
Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ.

Построение:

C 1

В 1

Выберите верный вариант:

1. НМ

1. МТ

А 1

D 1

1. Н T

Н

Т

С

В

М

А

D

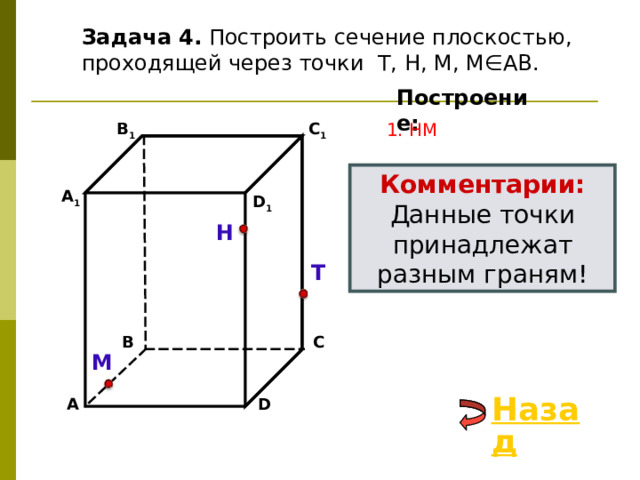
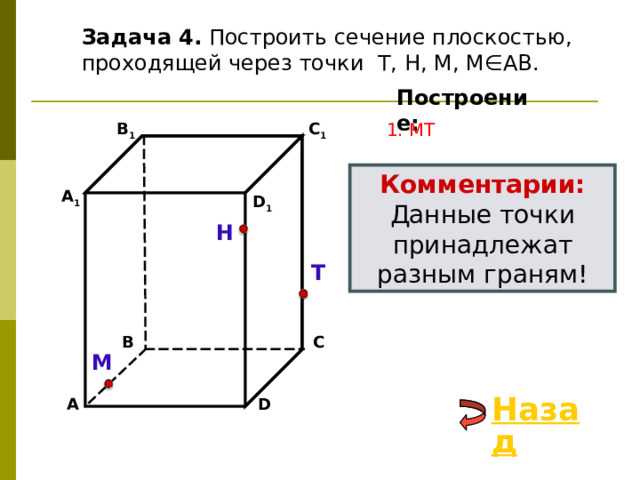
Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ.

Построение:

C 1

1. НМ

В 1

Комментарии:

Данные точки принадлежат разным граням!

А 1

D 1

Н

Т

В

С

М

Назад

D

А

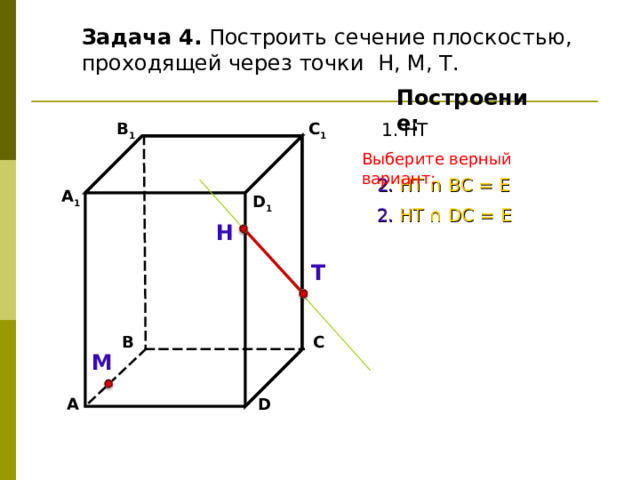
Задача 4. Построить сечение плоскостью, проходящей через точки Т, Н, М, М∈АВ.

Построение:

C 1

1. М T

В 1

Комментарии:

Данные точки принадлежат разным граням!

А 1

D 1

Н

Т

В

С

М

Назад

D

А

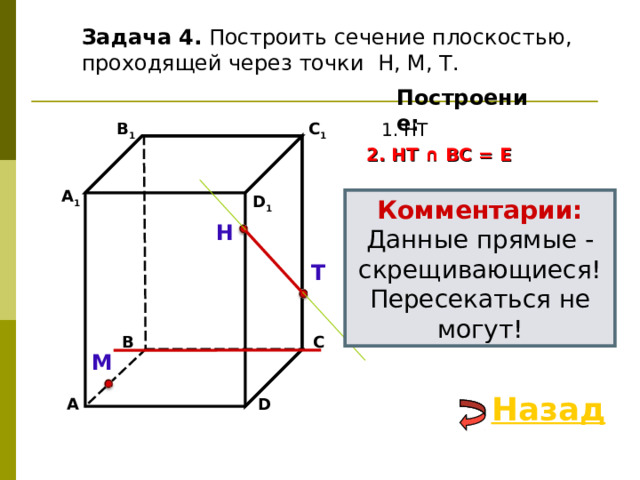
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

1. НТ

C 1

В 1

Выберите верный вариант:

2. НТ ∩ B С = Е

А 1

D 1

2. НТ ∩ D С = Е

Н

Т

С

В

М

D

А

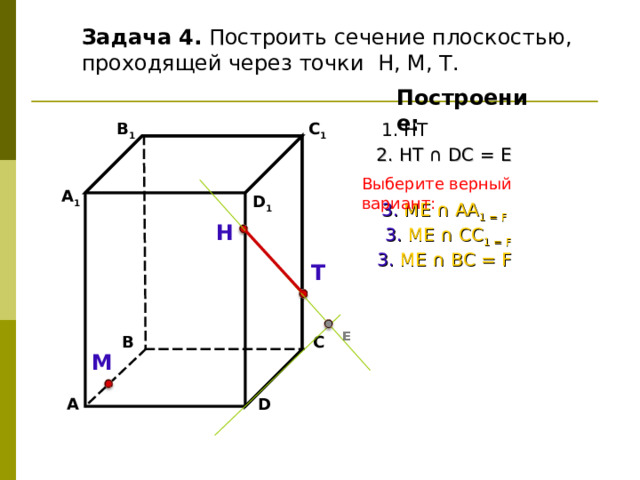
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

В 1

1. НТ

C 1

2. НТ ∩ ВС = Е

А 1

D 1

Комментарии:

Данные прямые - скрещивающиеся!

Пересекаться не могут!

Н

Т

С

В

М

Назад

D

А

Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

В 1

1. НТ

C 1

2. НТ ∩ D С = Е

Выберите верный вариант:

А 1

D 1

3 . ME ∩ AA 1 = F

Н

3 . ME ∩ CC 1 = F

3 . ME ∩ B С = F

Т

Е

В

С

М

D

А

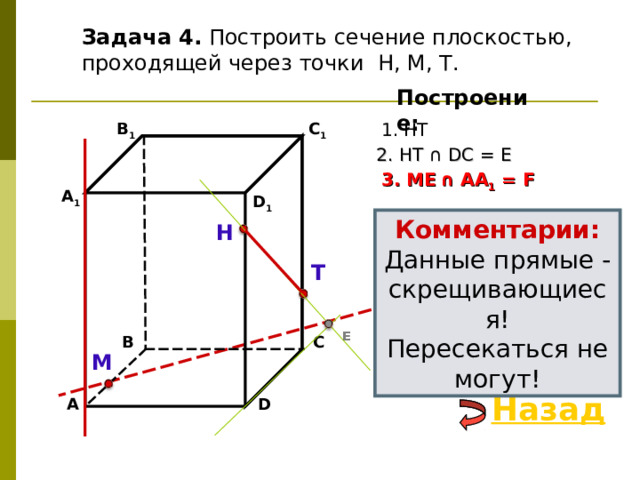
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

В 1

1. НТ

C 1

2. НТ ∩ D С = E

3 . ME ∩ AA 1 = F

А 1

D 1

Комментарии:

Данные прямые - скрещивающиеся!

Пересекаться не могут!

Н

Т

E

С

В

М

Назад

D

А

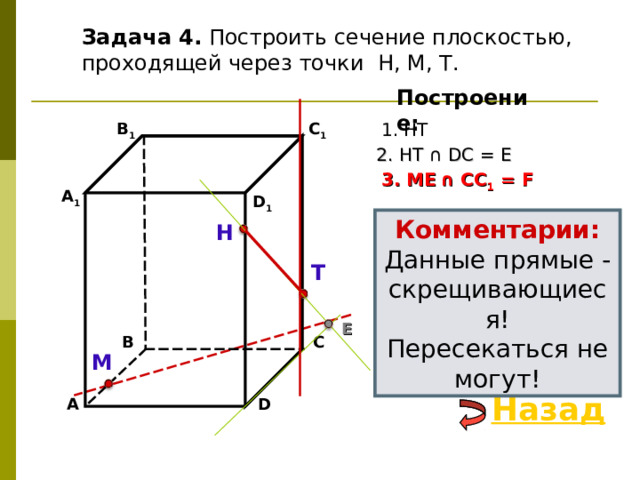
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

В 1

1. НТ

C 1

2. НТ ∩ D С = E

3 . ME ∩ CC 1 = F

А 1

D 1

Комментарии:

Данные прямые - скрещивающиеся!

Пересекаться не могут!

Н

Т

E

С

В

М

Назад

D

А

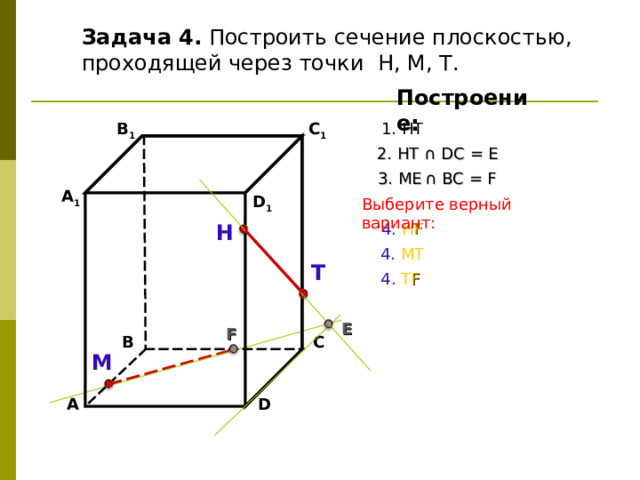
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

В 1

C 1

2. НТ ∩ D С = E

3 . ME ∩ ВС = F

А 1

D 1

Выберите верный вариант:

Н

4. Н F

4. МТ

Т

4. Т F

E

F

В

С

М

D

А

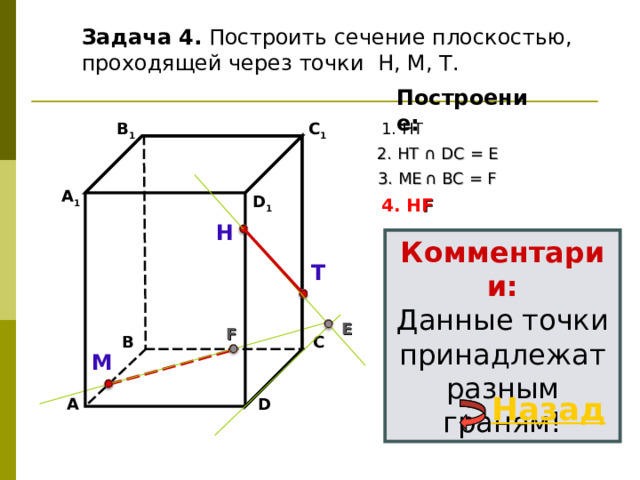
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

В 1

C 1

2. НТ ∩ D С = E

3 . ME ∩ ВС = F

А 1

D 1

4. Н F

Н

Комментарии:

Данные точки принадлежат разным граням!

Т

E

F

В

С

М

Назад

D

А

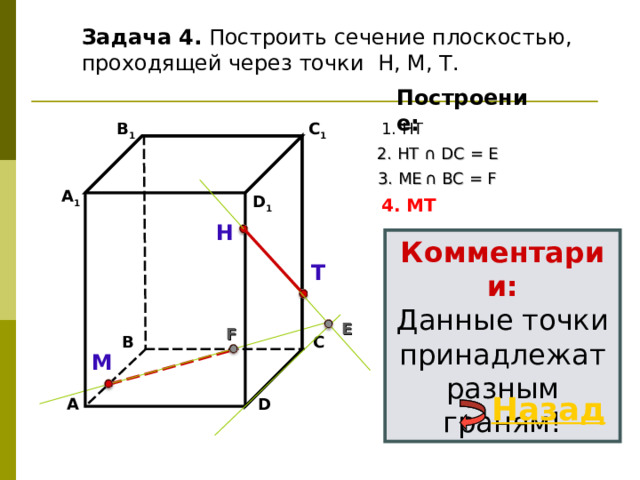
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

В 1

C 1

2. НТ ∩ D С = E

3 . ME ∩ ВС = F

А 1

D 1

4. MT

Н

Комментарии:

Данные точки принадлежат разным граням!

Т

E

F

В

С

М

Назад

D

А

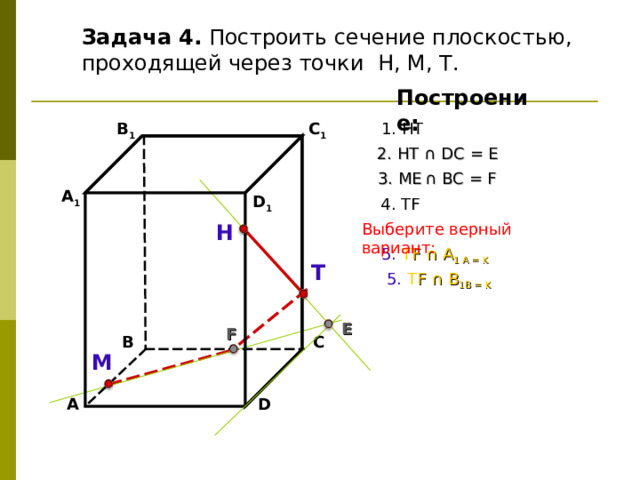
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

В 1

C 1

2. НТ ∩ D С = E

3 . ME ∩ ВС = F

А 1

D 1

4. Т F

Н

Выберите верный вариант:

5. Т F ∩ А 1 А = K

Т

5. Т F ∩ В 1 В = K

E

F

В

С

М

D

А

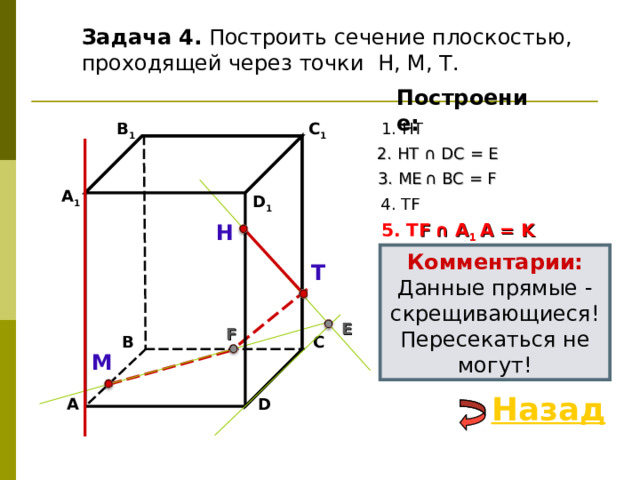
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

C 1

В 1

2. НТ ∩ D С = E

3 . ME ∩ ВС = F

А 1

D 1

4. Т F

5. Т F ∩ А 1 А = K

Н

Комментарии:

Данные прямые - скрещивающиеся!

Пересекаться не могут!

Т

E

F

С

В

М

Назад

А

D

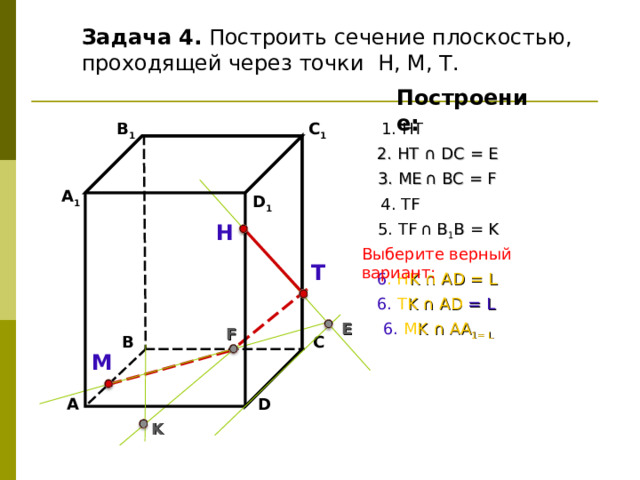
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

В 1

C 1

1. НТ

2. НТ ∩ D С = E

3 . ME ∩ ВС = F

А 1

D 1

4. Т F

5. Т F ∩ В 1 В = K

Н

Выберите верный вариант:

Т

6 . Н K ∩ А D = L

6. Т K ∩ А D = L

E

6. М K ∩ АА 1 = L

F

С

В

М

D

А

K

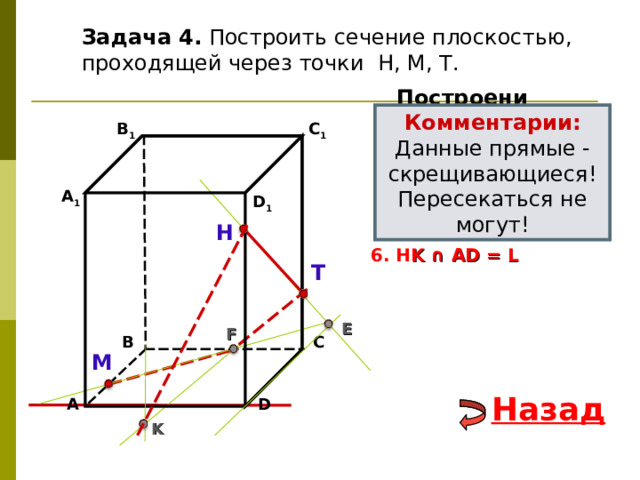
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

Комментарии:

Данные прямые - скрещивающиеся!

Пересекаться не могут!

В 1

C 1

1. НТ

2. НТ ∩ D С = E

3 . ME ∩ ВС = F

А 1

D 1

4. Т F

5. Т F ∩ В 1 В = K

Н

6. Н K ∩ А D = L

Т

E

F

С

В

М

Назад

D

А

K

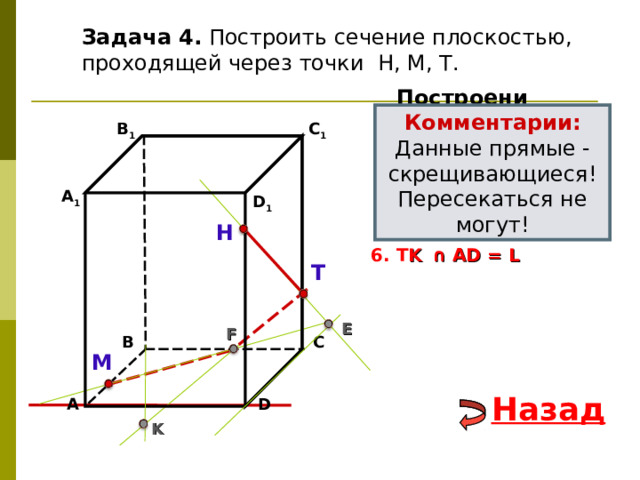
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

Комментарии:

Данные прямые - скрещивающиеся!

Пересекаться не могут!

В 1

1. НТ

C 1

2. НТ ∩ D С = E

3 . ME ∩ ВС = F

А 1

D 1

4. Т F

5. Т F ∩ В 1 В = K

Н

6. T K ∩ А D = L

Т

E

F

В

С

М

Назад

D

А

K

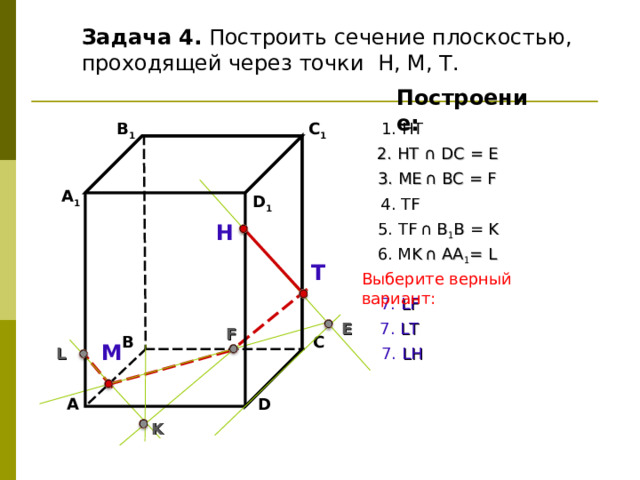
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

В 1

C 1

1. НТ

2. НТ ∩ D С = E

3 . ME ∩ ВС = F

А 1

D 1

4. Т F

5. Т F ∩ В 1 В = K

Н

6. М K ∩ АА 1 = L

Т

Выберите верный вариант:

7. LF

E

7. LT

F

В

С

М

7. LH

L

D

А

K

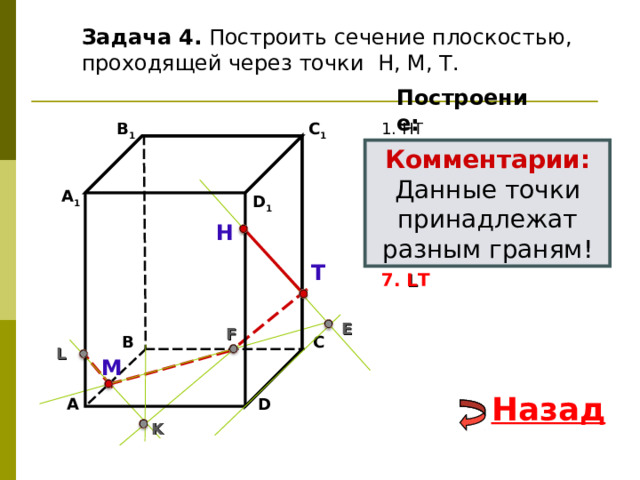
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

1. НТ

В 1

C 1

Комментарии:

2. НТ ∩ D С = E

Данные точки принадлежат разным граням!

3 . ME ∩ ВС = F

А 1

D 1

4. Т F

5. Т F ∩ В 1 В = K

Н

6. М K ∩ АА 1 = L

Т

7. L Т

E

F

В

С

L

М

Назад

D

А

K

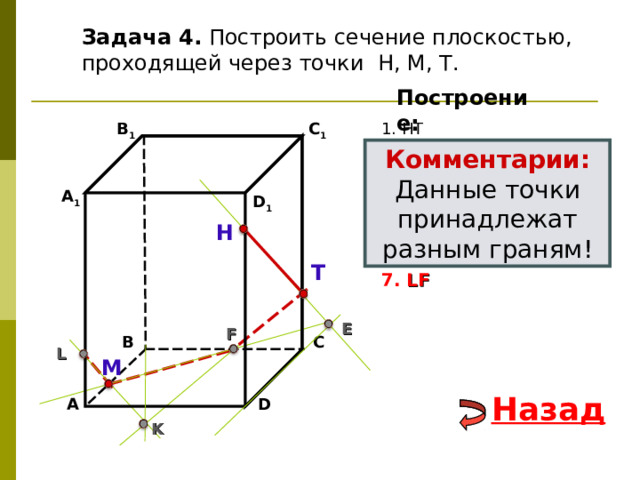
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

1. НТ

В 1

C 1

Комментарии:

2. НТ ∩ D С = E

Данные точки принадлежат разным граням!

3 . ME ∩ ВС = F

А 1

D 1

4. Т F

5. Т F ∩ В 1 В = K

Н

6. М K ∩ АА 1 = L

Т

7. LF

E

F

В

С

L

М

Назад

D

А

K

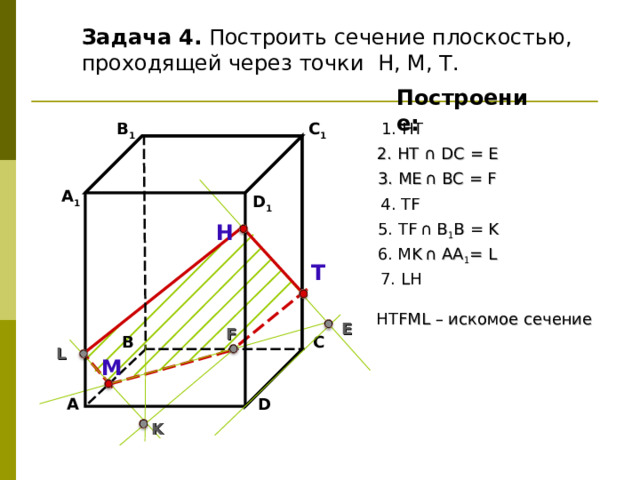
Задача 4. Построить сечение плоскостью, проходящей через точки Н, М, Т.

Построение:

В 1

C 1

1. НТ

2. НТ ∩ D С = E

3 . ME ∩ ВС = F

А 1

D 1

4. Т F

5. Т F ∩ В 1 В = K

Н

6. М K ∩ АА 1 = L

Т

7. L Н

НТ F М L – искомое сечение

E

F

В

С

L

М

D

А

K

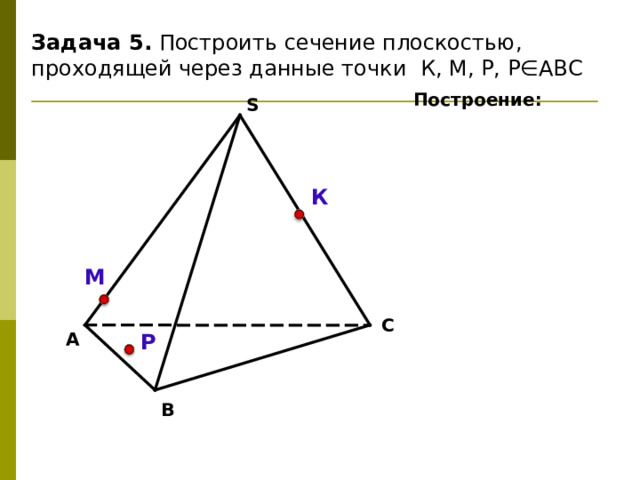
Задача 5. Построить сечение плоскостью, проходящей через данные точки К, М, Р, Р∈АВС

Построение:

S

К

М

С

А

Р

В

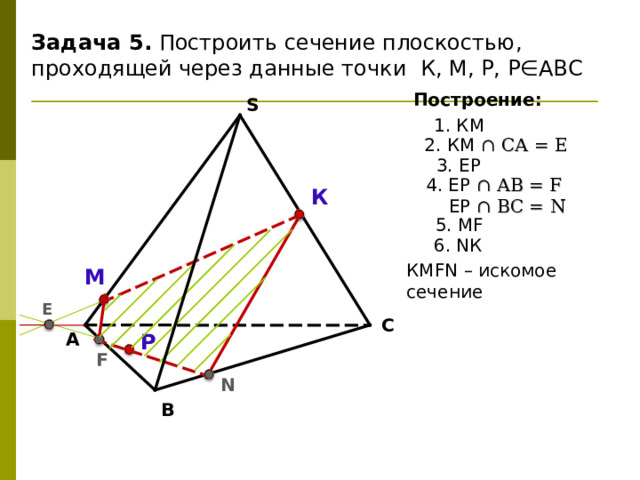
Задача 5. Построить сечение плоскостью, проходящей через данные точки К, М, Р, Р∈АВС

Построение:

S

1. КМ

2. КМ ∩ СА = Е

3. E Р

4 . ЕР ∩ АВ = F

ЕР ∩ В C = N

К

5 . М F

6 . N К

КМ FN – искомое сечение

М

Е

С

Р

А

F

N

В