Цель урока: формирование навыков решения задач на построение сечений в многогранниках.
Обучающая цель: обобщить и систематизировать знания, умения и навыки при построении сечений многогранников методом следов, выполняя чертежи в компьютерной программе «Geometry».
Развивающая цель: формировать и развивать логическое мышление, пространственное воображение, графическую культуру и математическую речь.
Воспитательная цель: воспитывать познавательный интерес к предмету, воспитывать чувство сплоченности, взаимопомощи, воспитывать умения работать индивидуально над задачей.
Существует три основных метода построения сечений многогранников:
Метод следов.
Метод вспомогательных сечений.
Комбинированный метод.
Первые два метода являются разновидностями аксиоматического метода построения сечений.
Можно также выделить следующие методы построения сечений многогранников:
построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;
построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.
Рассмотрим методы построения сечений на решении задач.
Задача 1. Построить сечение треугольной призмы ABCFED плоскостью α, которой принадлежат точки G,H,I.
1 шаг. Открываем компьютерную программу «Geometry»: на Рабочем столе щёлкаем дважды ЛКМ на пиктограмме. В открытом окне в меню инструментов выбираем отрезок и строим треугольную призму ABCFED, отмечаем на рёбрах точки сечения:
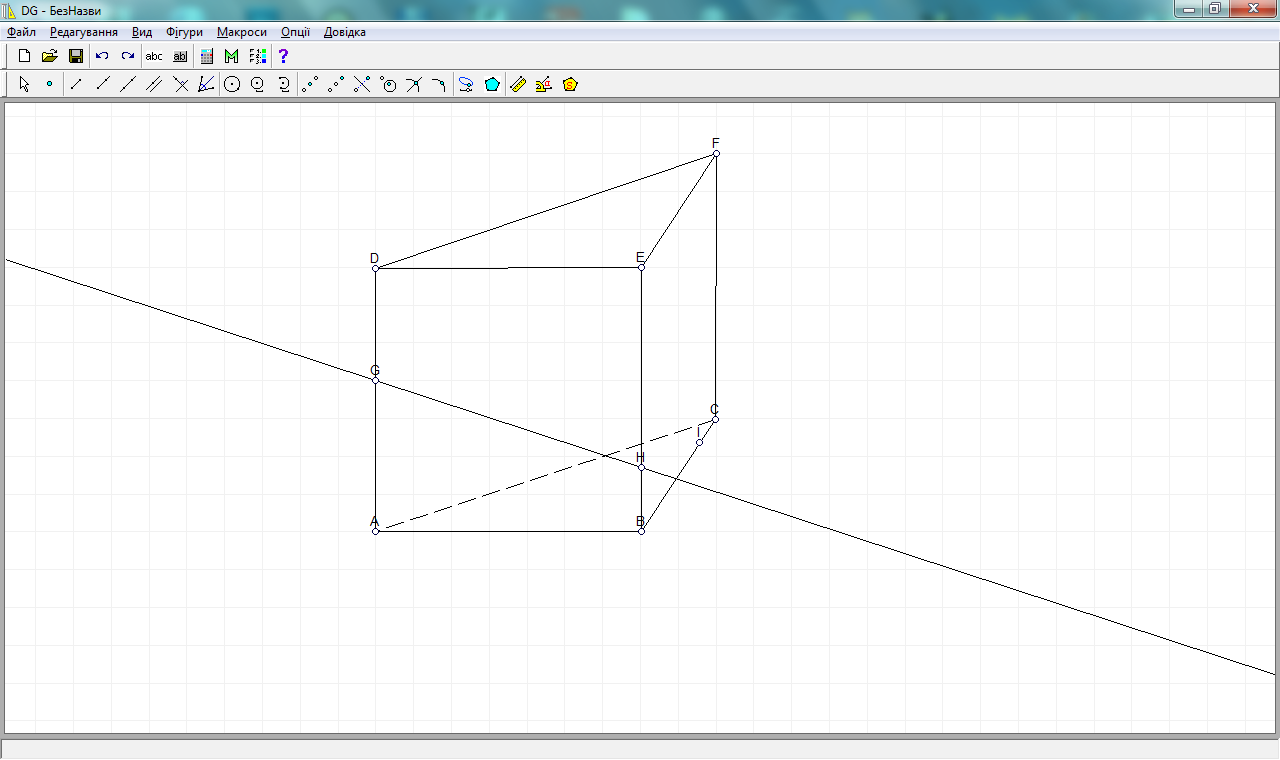
2 шаг. Выбираем Прямую на панели и проводим её через точки G и H, так как данные точки принадлежат одной плоскости (ADEB).
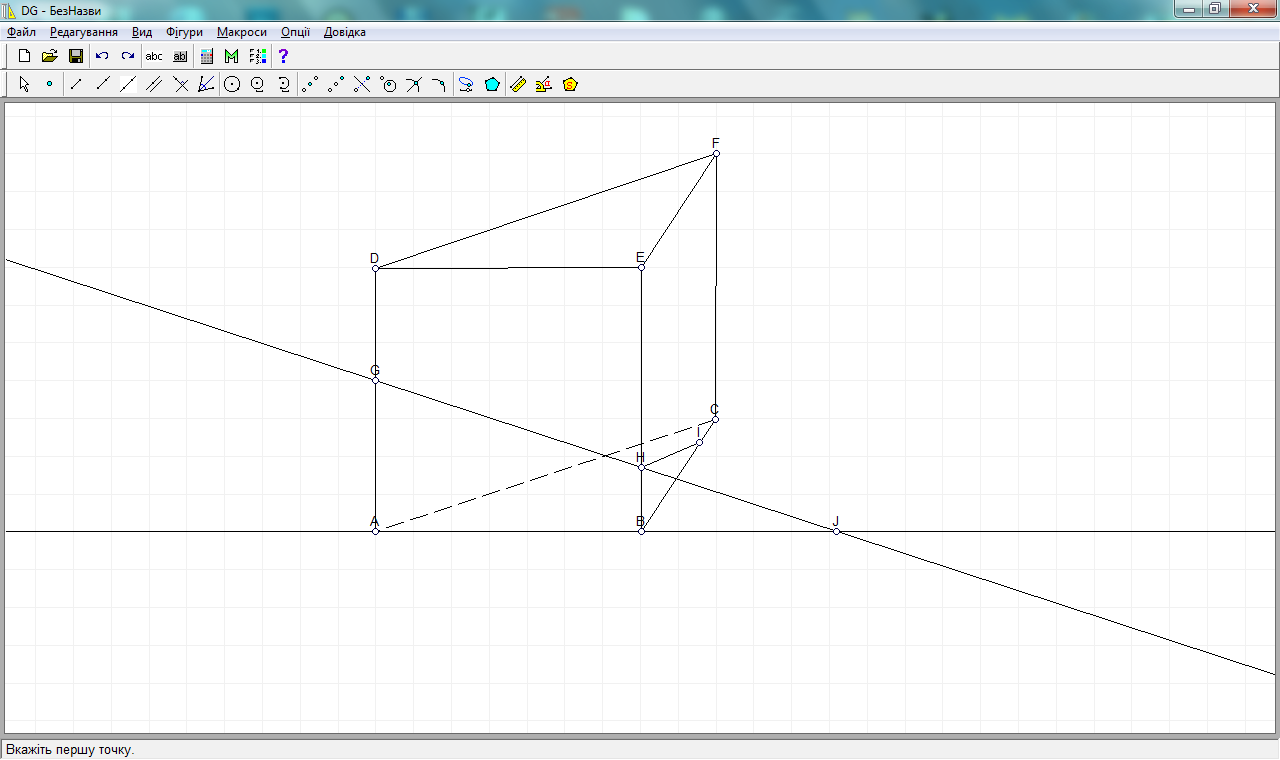
3 шаг. Аналогично проводим прямую через точки H и I, также проводим прямую через ребро призмы АВ. Отмечаем точку пересечения J прямых АВ и GH.
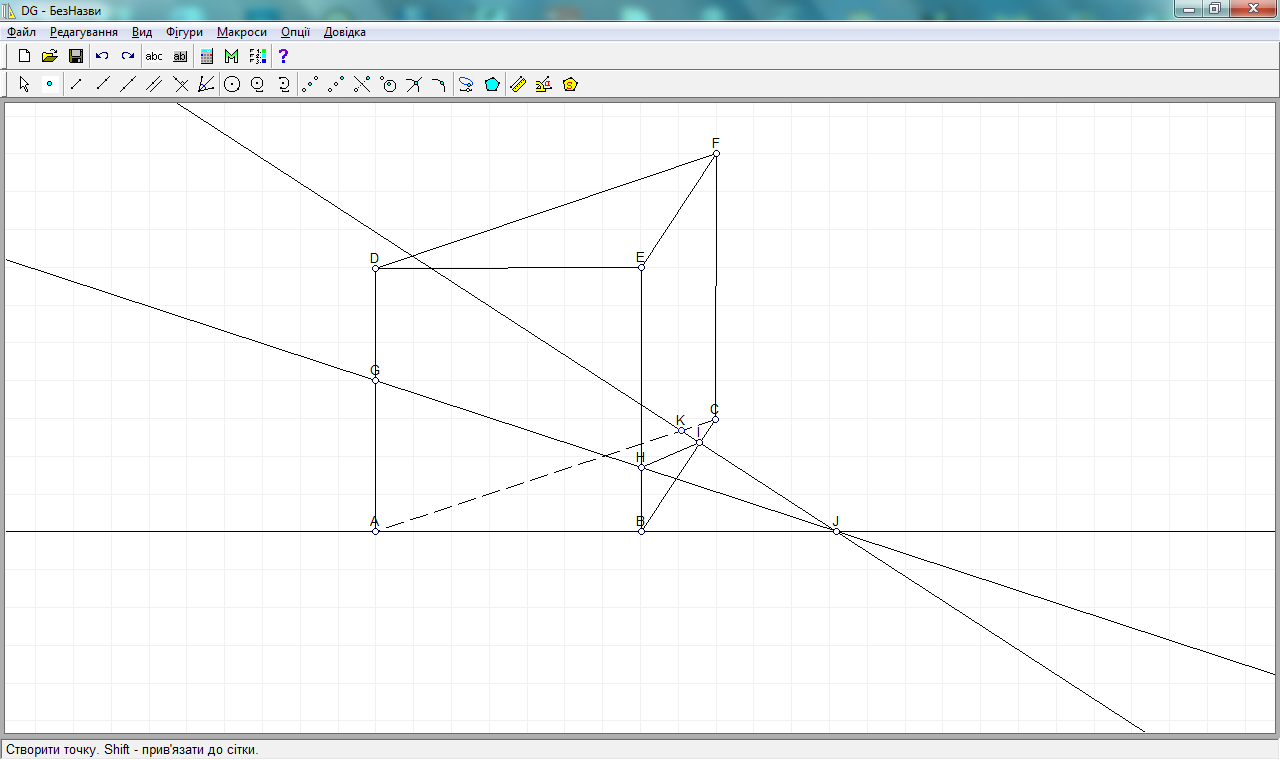
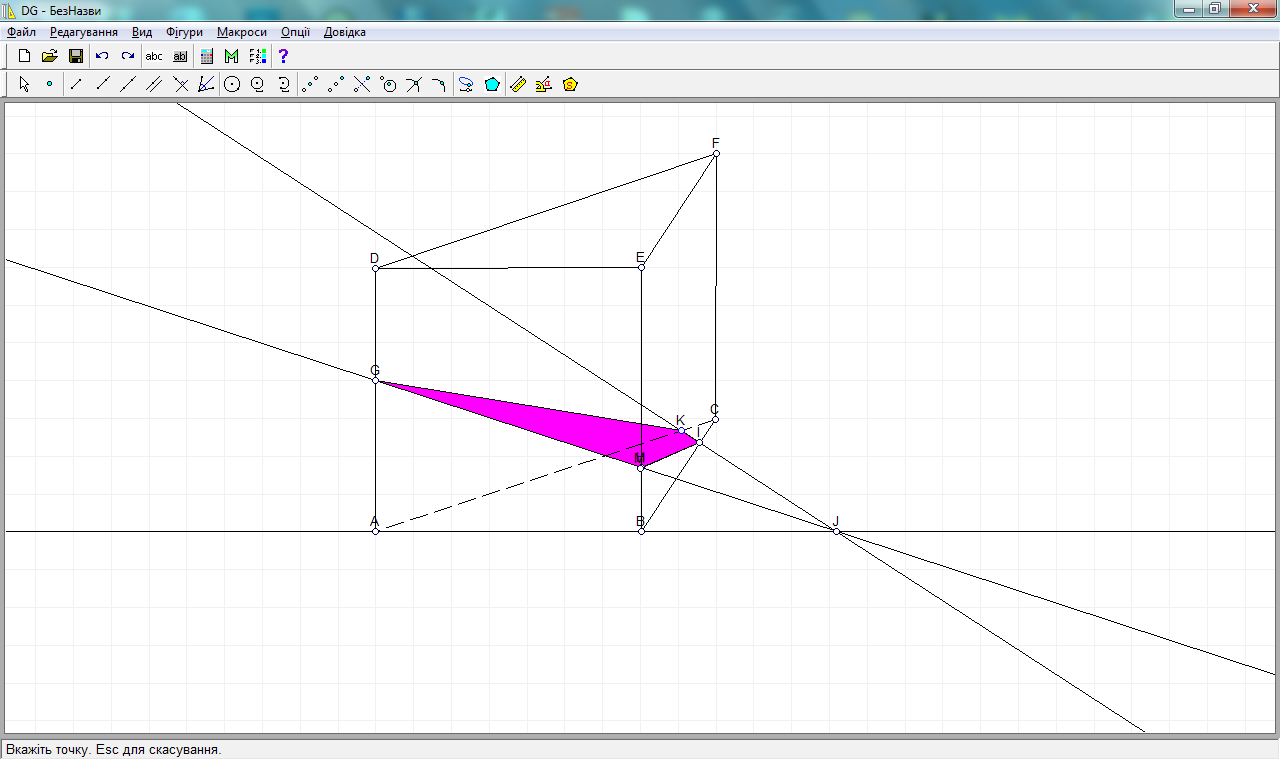
4 шаг. Проводим прямую через точки I и J, так как они принадлежат плоскости (АВС). Отмечаем точку пересечения К на ребре АС.
5 шаг. Строим отрезок GK, получаем сечение GKIH.
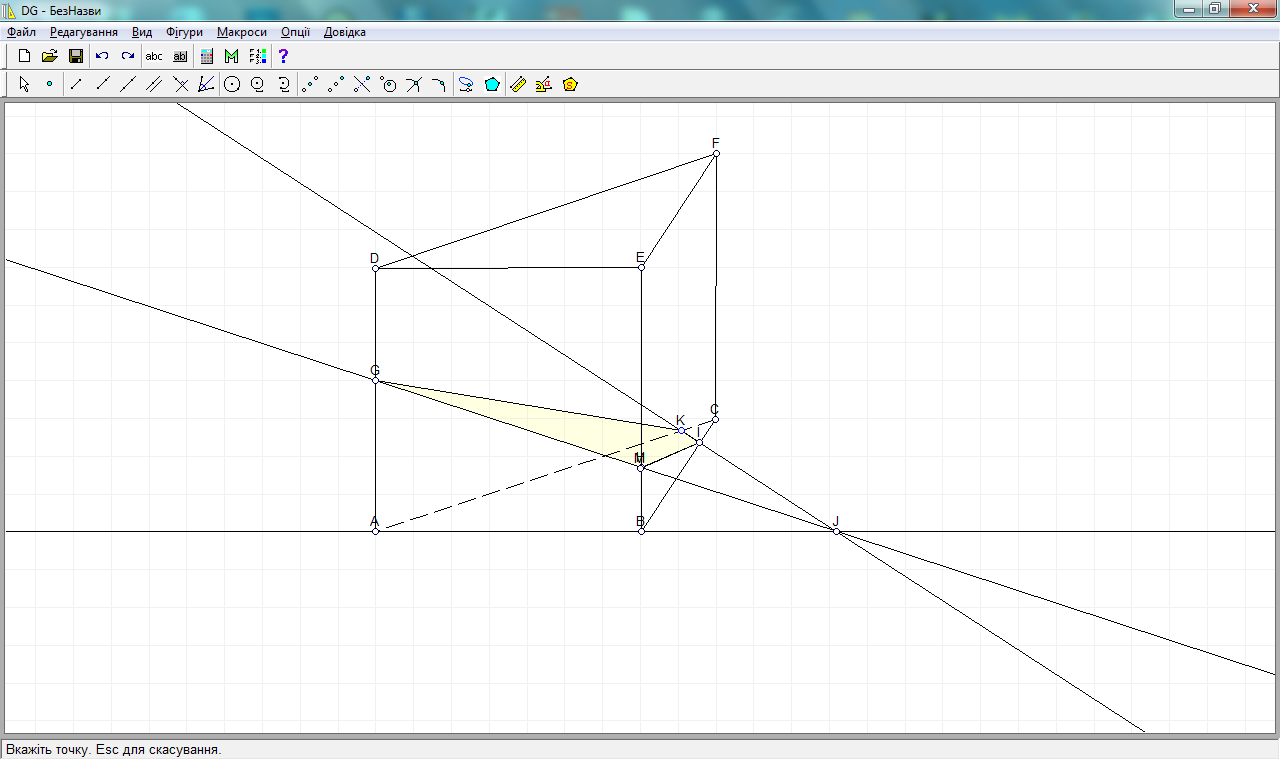
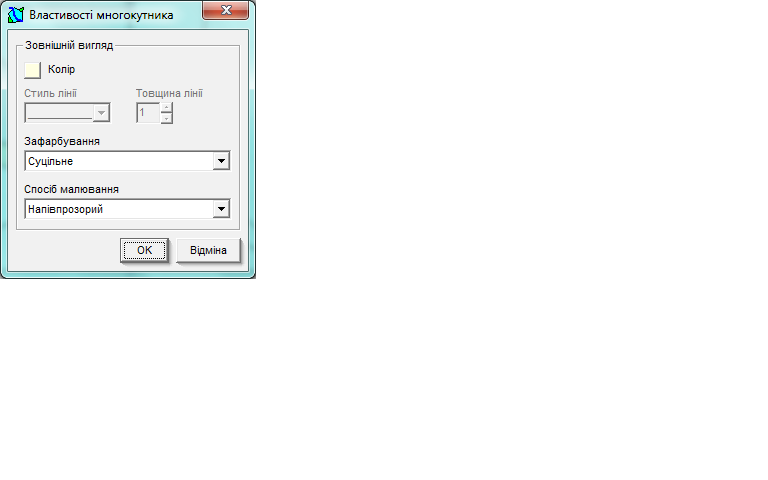
6 шаг. Выбираем на панели Многоугольник и нажимаем на точки полученного сечения GKIH, выбираем свойства многоугольника, меняем цвет его штриховки.
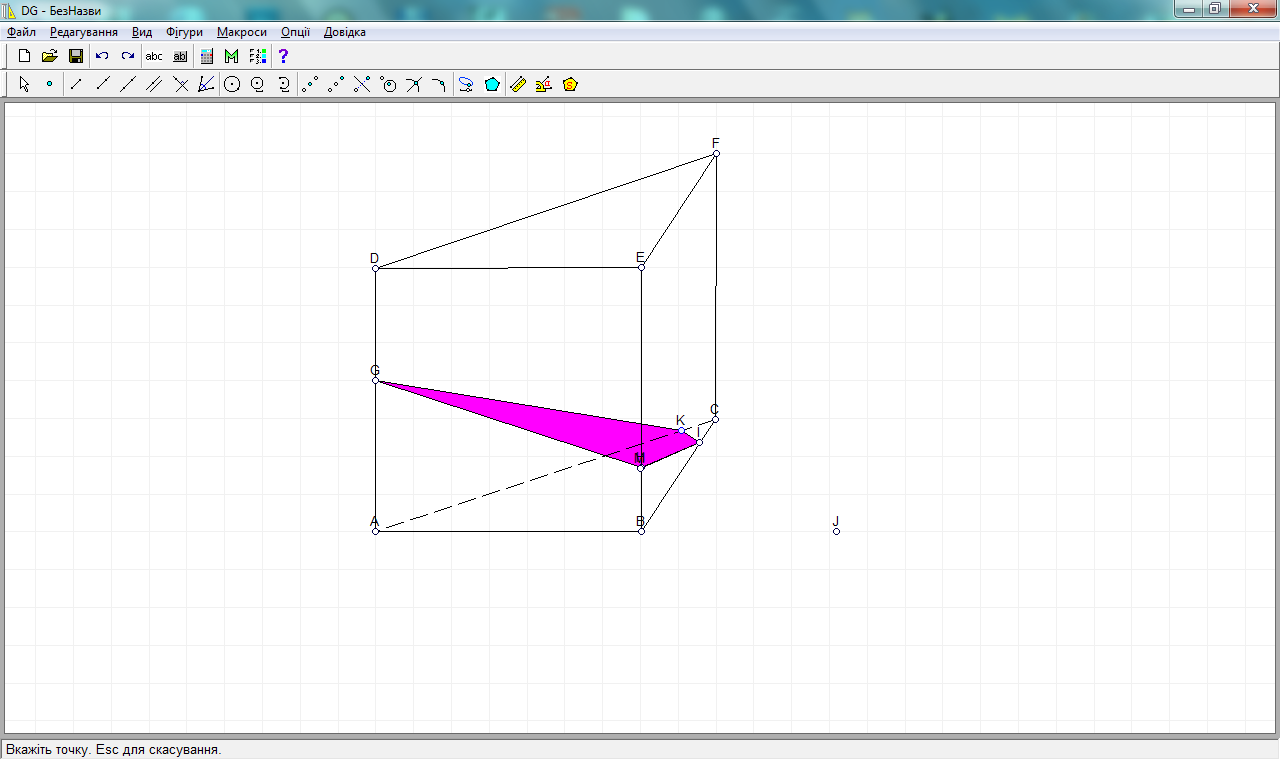
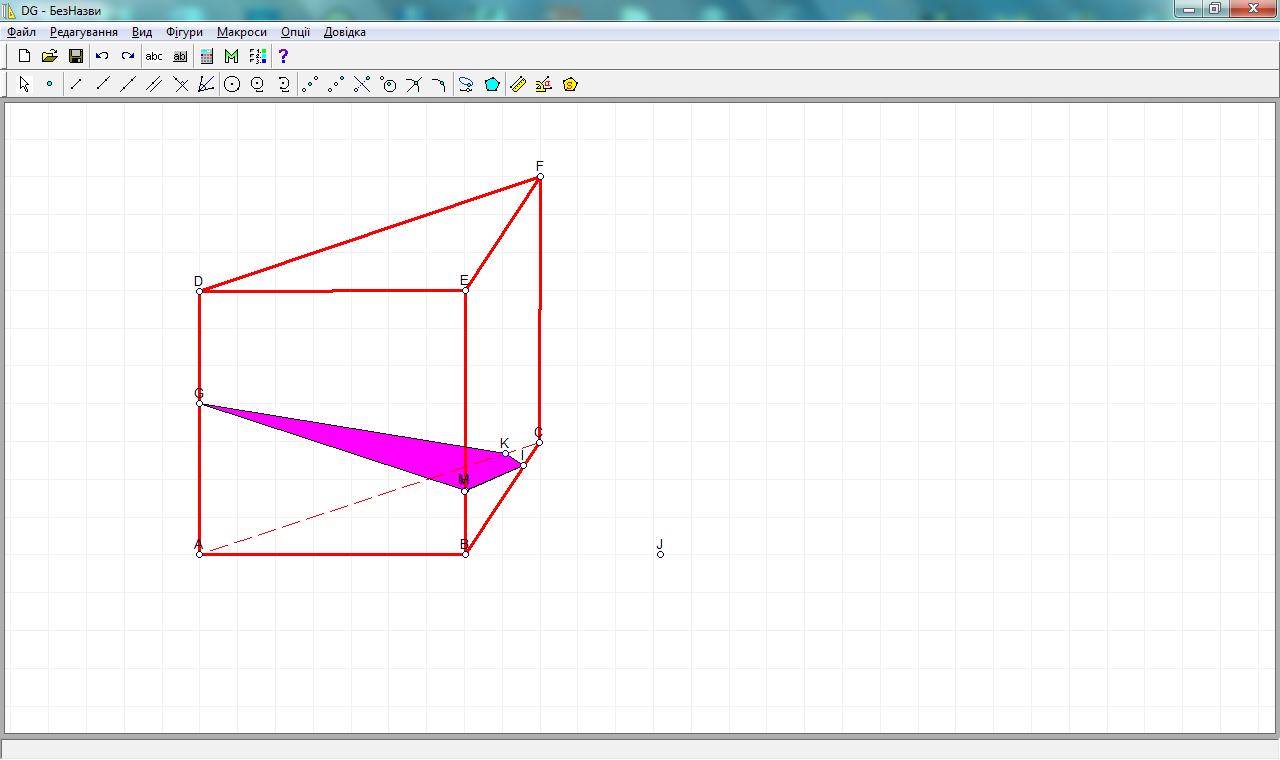
7 шаг. Удаляем все прямые, нажав на каждую ПКМ→удалить, и изменяем для чёткости и яркости цвет рёбер треугольной призмы.
В результате получим компьютерное изображение нашего сечения.
Аналогично строим все элементы к задачам 2,3,4,5 и выделяем сечения.
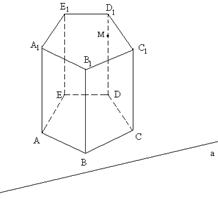
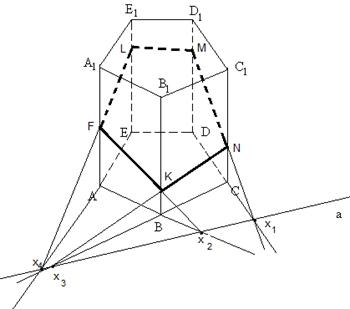
Задача 2. Построить сечение призмы ABCDEA1B1C1D1E1 плоскостью α, которая задана следом a в плоскости (ABC) основания призмы и точки M, принадлежащей ребру DD1.
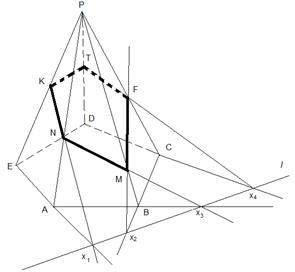
Задача 3. Построить сечение пятиугольной пирамиды PABCDE плоскостью, которая задана следом l и точкой K ребра PE.
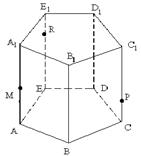
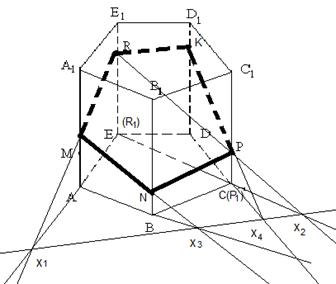
Задача 4. Построить сечение призмы ABCDEA1B1C1D1E1 плоскостью , где M, P, R являются точками соответственно ребер AA1, CC1, EE1.
Задача 5. Точки P, Q, R взяты на поверхности параллелепипеда ABCDA1B1C1D1 следующим образом: точка P лежит в грани CC1D1D, точка Q – в грани СC1D1D точка R лежит на прямой BB1 (вне отрезка BB1). Построить сечение параллелепипеда плоскостью PQR.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



 . В открытом окне в меню инструментов выбираем отрезок и строим треугольную призму ABCFED, отмечаем на рёбрах точки сечения:
. В открытом окне в меню инструментов выбираем отрезок и строим треугольную призму ABCFED, отмечаем на рёбрах точки сечения:





 6шаг. Выбираем на панели Многоугольник и нажимаем на точки полученного сечения GKIH, выбираем свойства многоугольника, меняем цвет его штриховки:
6шаг. Выбираем на панели Многоугольник и нажимаем на точки полученного сечения GKIH, выбираем свойства многоугольника, меняем цвет его штриховки:









 Практическая работа по математике "Построение сечений с использованием информационных и телекоммуникационных технологий" (0.97 MB)
Практическая работа по математике "Построение сечений с использованием информационных и телекоммуникационных технологий" (0.97 MB)
 0
0 1991
1991 513
513 Нравится
0
Нравится
0











