Цель: Обобщить и систематизировать полученные знания и умения по данной теме
Задачи:
Преодоление страха перед пространственным видением материала, возможность проследить все этапы построения сечений с помощью ПК в графическом редакторе и проверить правильность выполнения заданий.
Закрепить умение формировать информационное пространство и применять программное обеспечение при решении задач по геометрии
Начальные сведения по стереометрии имеют абстрактный характер, усвоение материала строится на заучивании, и таким образом, намечается формализм в знаниях учащихся. Они теряют интерес к предмету, и многие из них считают стереометрию трудным школьным предметом. В данной разработке наглядно представлен процесс построения сечений не только на примере призмы, но и на примере пирамиды. Материал будет полезен при закреплении соответствующей темы.
Конспект урока.
Интегрированный урок
математика + информатика
Цели урока:
Обобщить изученный материал по теме « Графический редактор векторного типа», в ходе практической работы по информатике, а также обобщить и систематизировать полученные знания и умения по теме « Построение сечений многогранников»;
Проверить степень усвоения учащимися знаний по данным темам. Проконтролировать степень усвоения знаний по теме « Графический редактор» при построении сечений многогранников;
Закрепить умение формировать информационное пространство и применять программное обеспечение при решении задач по геометрии;
Показать, что предметы не изолированы друг от друга и навыки, полученные при изучении информатики, можно с успехом применять при изучении геометрии.
Урок проводиться в 11 классе после изучения темы Многогранники».
Геометрия изучается по учебнику « Геометрия 10-11» автора Погорелова А.В.,
Оборудование: Компьютеры, мультимедийный проектор, экран, набор карточек с дифференцированными заданиями для индивидуальной и парной работы.
Программное обеспечение: операционная система Windows XP, текстовый редактор MS Word.
ХОД УРОКА
1. Организационный момент( 2 мин)
Краткий инструктаж по технике безопасности.
2. Актуализация опорных знаний
Вопросы, которые надо обсудить
1) Дать определение многогранника
2) Какой многогранник называется выпуклым?
3) Что такое грань выпуклого многогранника, ребро, вершина?
4) Что значит построить сечение многогранника плоскостью?
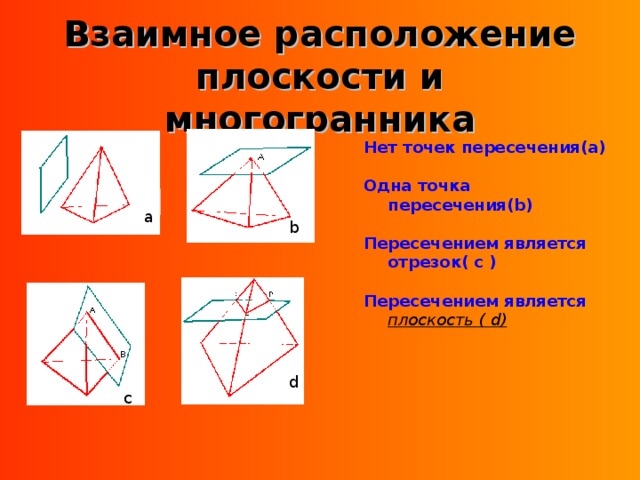
5) Как могут располагаться относительно друг друга многогранник и плоскость?
6) Как задается плоскость?
7) Когда задача на построение сечения многогранника плоскостью считается решенной?
10) Дайте определение сечения многогранника.
11) Что значит построить сечение многогранника плоскостью?
12) Сколько точек необходимо, чтобы однозначно провести прямую на плоскости?
13) Какая фигура получается при пересечении двух плоскостей? (показать на модели)
14) Где располагается точка пересечения плоскости и прямой лежащей в другой плоскости?
АЛГОРИТМ ПОСТРОЕНИЯ СЕЧЕНИЙ
Для построения сечения нужно найти прямые, по которым плоскость сечения пересекается с плоскостями граней многогранника.
Для построения прямой пересечения плоскостей, находят две её точки, через них и проводят прямую пересечения.
Точки прямой пересечения отыскиваются как точки пересечения известной прямой, лежащей в одной плоскости, со второй плоскостью.
Для построения такой точки пересечения данных прямой и плоскости в этой плоскости находят прямую, пересекающую данную, -искомая точка получается в пересечении этих прямых.
Существует три основных метода построения сечений многогранников:
Метод следов.
Метод вспомогательных сечений.
Комбинированный метод.
Первые два метода являются разновидностями Аксиоматического метода построения сечений.
Будем рассматривать только случай, когда плоскость пересекает многогранник по его внутренности. При этом пересечением данной плоскости с каждой гранью многогранника будет некоторый отрезок. Таким образом, задача считается решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника.

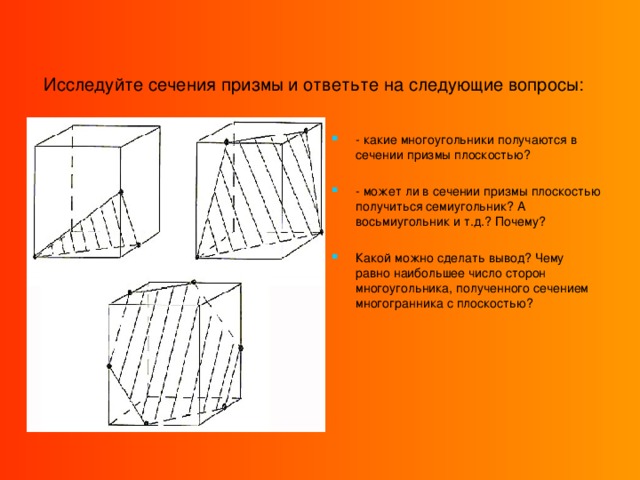
Исследуйте сечения призмы (слайд 16) и ответьте на следующие вопросы:- какие многоугольники получаются в сечении призмы плоскостью? (Важно число сторон многоугольника);
[ Предполагаемые ответы: треугольник, четырехугольник, пятиугольник, шестиугольник.]
- может ли в сечении призмы плоскостью получиться семиугольник? А восьмиугольник и т.д.? Почему?
Давайте рассмотрим призму и ее возможные сечения плоскостью ( на модели). Какие многоугольники получаются?
Какой можно сделать вывод? Чему равно наибольшее число сторон многоугольника, полученного сечением многогранника с плоскостью?
[ Наибольшее число сторон многоугольника, полученного в сечении многогранника плоскостью, равно числу граней многогранника.]
а) Метод следов заключается в построении следов секущей плоскости на плоскость каждой грани многогранника. Построение сечения многогранника методом следов обычно начинают с построения так называемого основного следа секущей плоскости, т.е. следа секущей плоскости на плоскости основания многогранника.
б) Метод вспомогательных сечений построения сечений многогранников является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь ввиду, что построения, выполняемые при использовании этого метода, зачастую получаются “скученными”. Тем не менее в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.
Метод следов и метод вспомогательных сечений являются разновидностями аксиоматического метода построения сечений многогранников плоскостью.
в) Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.
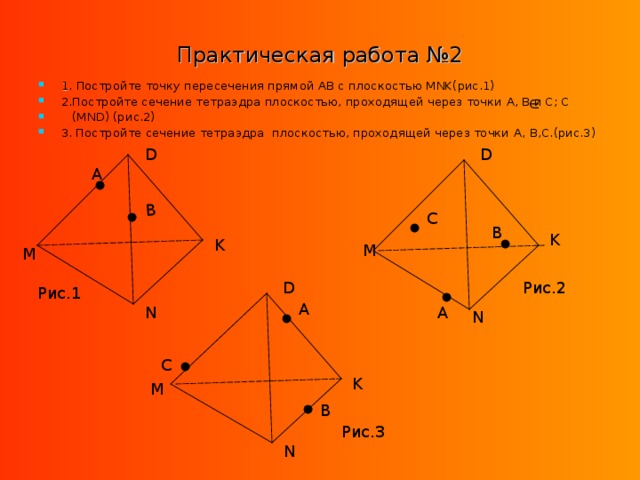
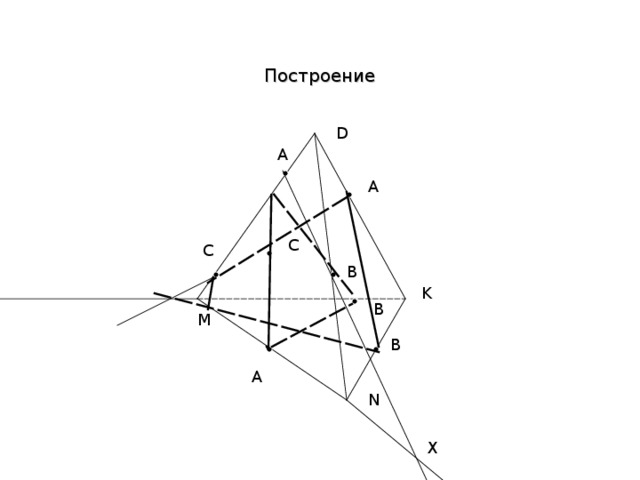
SHAPE * MERGEFORMAT А теперь на примере решения задач рассмотрим метод следов.
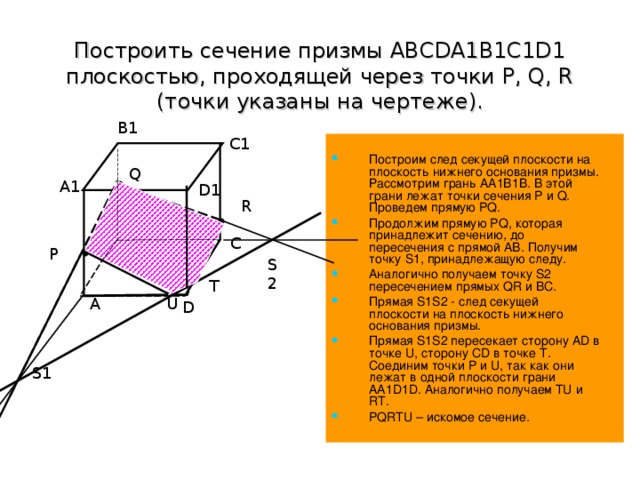
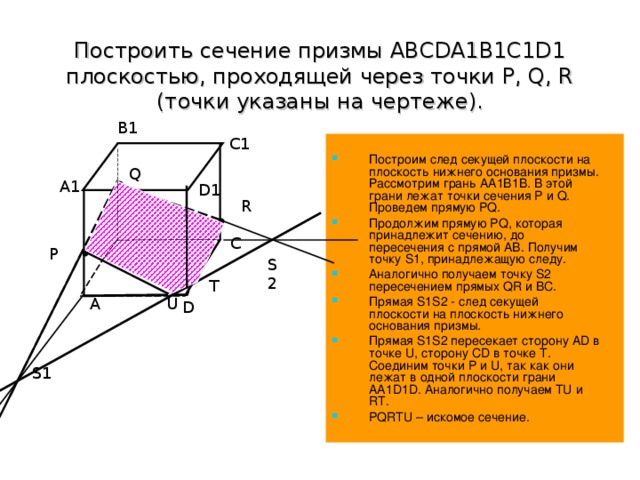
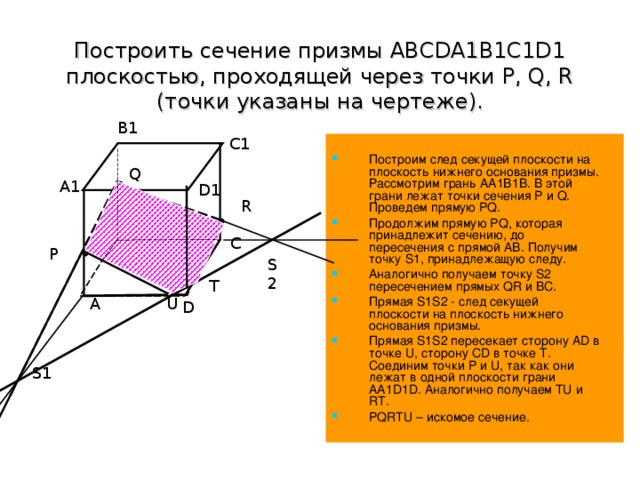
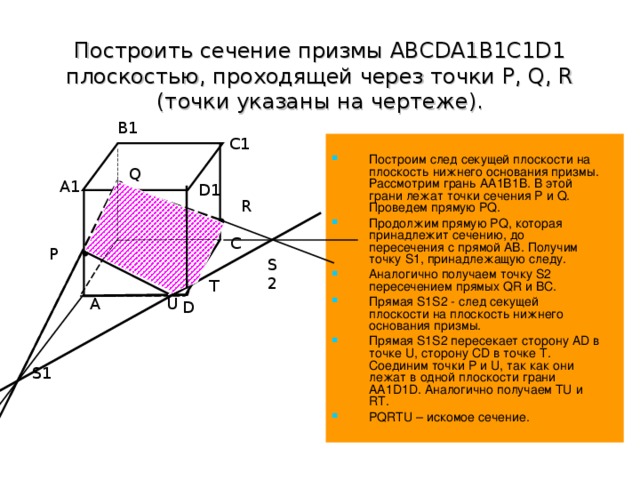
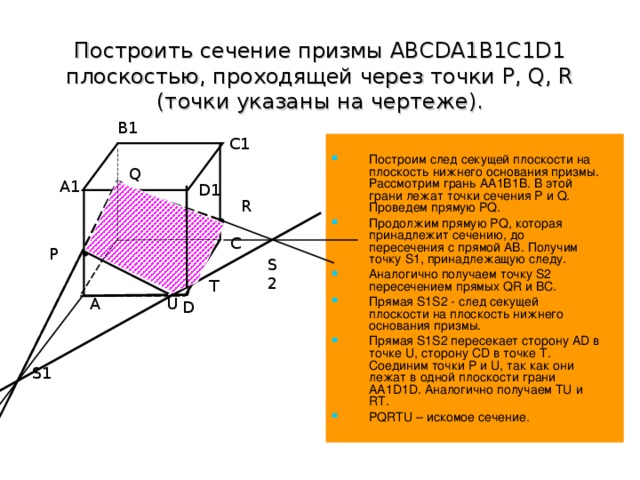
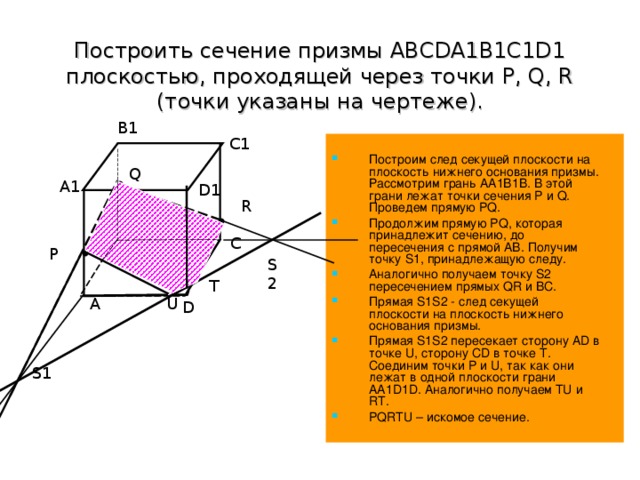
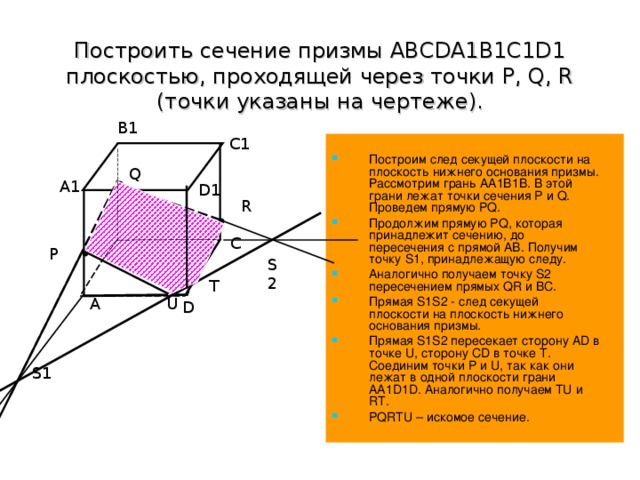
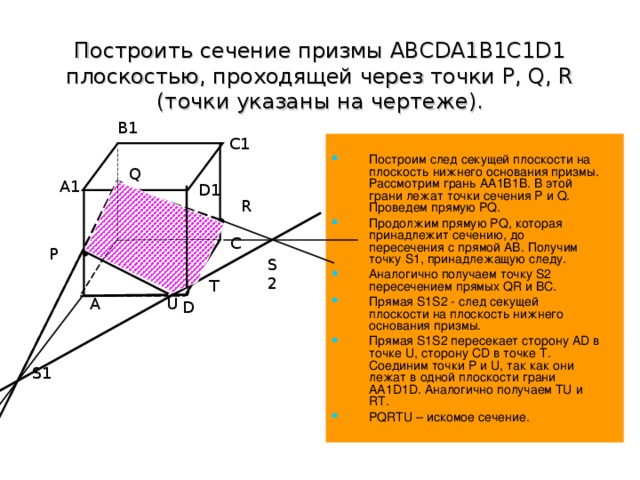
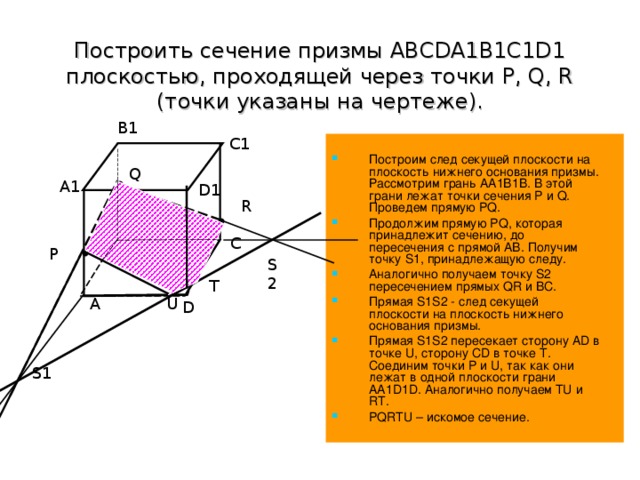
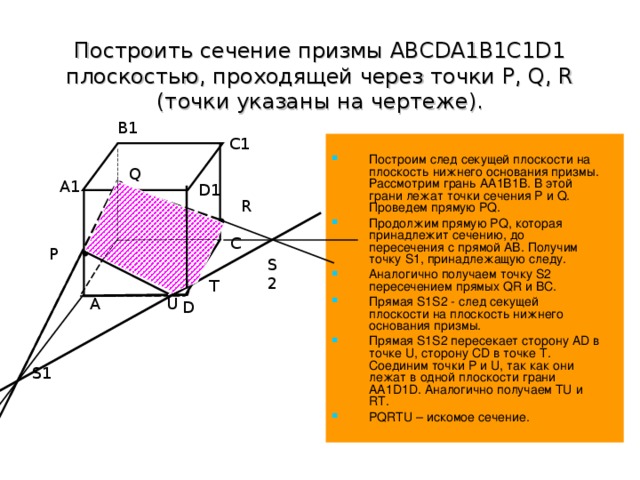
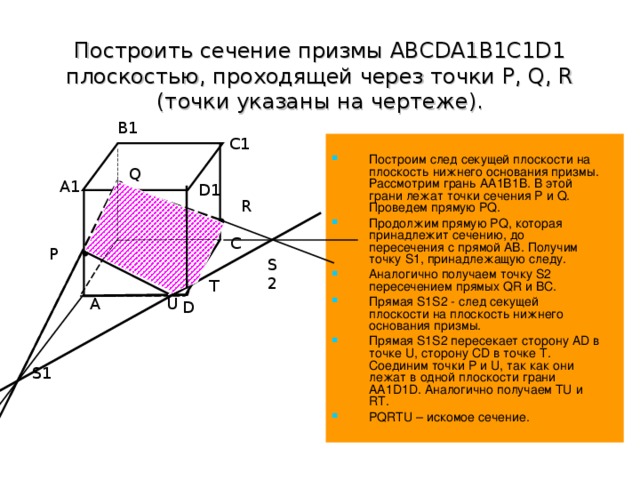
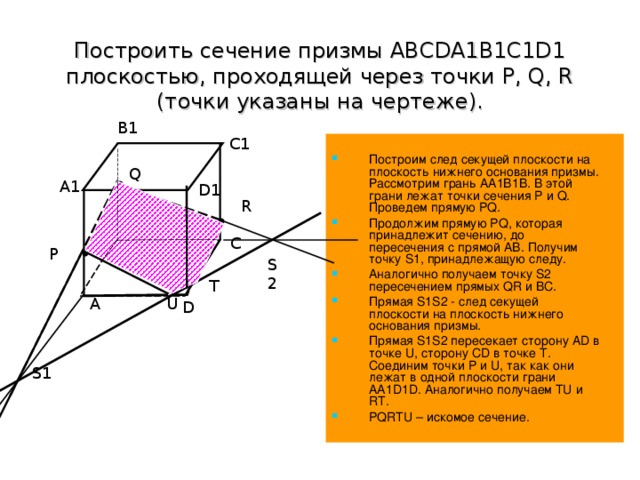
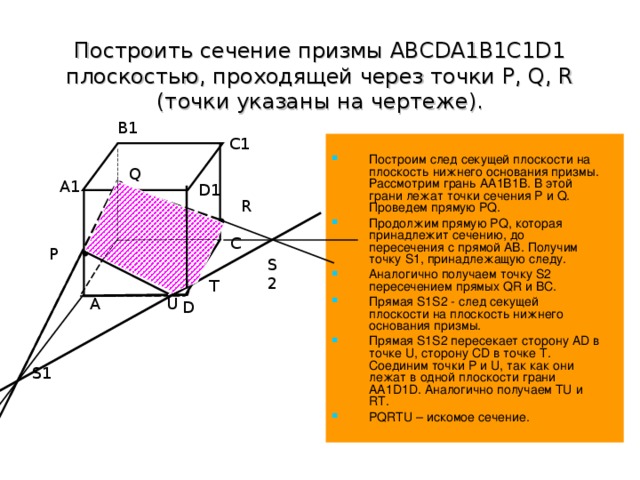
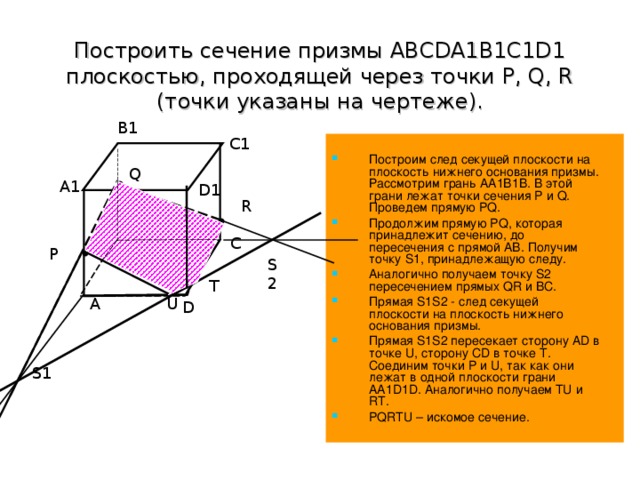
Построить сечение призмы ABCDA1B1C1D1 плоскостью, проходящей через точки P, Q, R (точки указаны на чертеже).
Решение.( слайд 18)
Построим след секущей плоскости на плоскость нижнего основания призмы. Рассмотрим грань АА1В1В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.
Продолжим прямую PQ, которая принадлежит сечению, до пересечения с прямой АВ. Получим точку S1, принадлежащую следу.
Аналогично получаем точку S2 пересечением прямых QR и BC.
Прямая S1S2 - след секущей плоскости на плоскость нижнего основания призмы.
Прямая S1S2 пересекает сторону AD в точке U, сторону CD в точке Т. Соединим точки P и U, так как они лежат в одной плоскости грани АА1D1D. Аналогично получаем TU и RT.
PQRTU – искомое сечение.
Вопросы по информатике:
Какую программу можно использовать для построения многогранников и их сечений плоскостями?
Каков принцип построения в данном графическом редакторе?
При помощи каких графических примитивов получено это изображение?
Как поставить точки?
Как обозначить точки?
Вывод:
Порядок построения чертежа
1. Построить прямоугольник
2. Объем - Настройка объема
3. На панели Настройка объема открыть кнопку Поверхность и выбрать тип поверхности Каркас
4. На панели Настройка объема открыть кнопку Глубина и увеличить глубину
5. Расставить обозначения. Для этого:
выбрать на панели Рисование кнопку Надпись
нарисовать прямоугольник
дважды щелкнуть по границе
выбрать Цвет линий – Нет линий
вписать в прямоугольник букву
скопировать Надписи ко всем вершинам и расставить буквы (при обозначении верхних вершин использовать кнопку Подстрочный) 6.Поставим точки, через которые будет проходить сечение.
Для этого нарисуем окружность, зальем ее красным цветом, скопируем и получим три точки. Используя Надписи, расставим обозначения точек
3.Практическая работа в парах( слайды 38,35)
Практическая работа заключается в построении на компьютере многогранников и их сечений. Учащиеся занимают места за компьютером по принципу: сильный-слабый. Задание выполняет слабый ученик, сильный выступает в роли консультанта и при необходимости оказывает помощь в построении чертежа, контролирует правильность выполнения задания.
В ходе выполнения практической работы учитель информатики уделяет особое внимание работающим парах: как проходит консультирование и выполнение заданий более слабым учеником.
Учитель математики контролирует правильность выполнения чертежей, даёт индивидуальные консультации в ходе работы.
4.Анализ работы
Проверка построения на мультимедиа проекторе, решение рассказывается устно
5. Домашнее задание
Каждому ученику раздаётся индивидуальное задание на карточке по построению сечений.
6.Итог урока
Учитель математики подводит итог урока по теме « построение сечений многогранников», учитель информатики по теме
« графический редактор».
Результативность
В результате работы с компьютерной презентацией у старшеклассников активизируется интерес к изучаемому предмету и появляется стимул к освоению более сложных тем. Применение данной технологии на уроках позволило развить у учащихся навык решения задач на построение сечений многогранников. Это привело к повышению качества выполнения проверочных работ по данным темам на 10% и выше (по сравнению с другим классом, где обучение велось традиционно).
Информационные ресурсы по теме ( используемая литература, электронные материалы, Интернет-сайты и т.д.
В.С. Крамор « Повторяем и систематизируем школьный курс геометрии»
Москва « Просвещение»,1992 г.
2. В.А. Гусев, В.Н. Литвиненко, А.Г. Мордкович « Практикум по элементарной математики. Геометрия». Москва « Просвещение»,1992 г.
3. Газета « Математика» № 6,7, 2004.
4. http://polyhedron2008.narod.ru/pages/polyhedr.htm
5. http://festival.1september.ru/articles/212754/

 Получите свидетельство
Получите свидетельство Вход
Вход


































 Построение сечений в многогранниках (1.74 MB)
Построение сечений в многогранниках (1.74 MB)
 1
1 3697
3697 617
617 Нравится
0
Нравится
0


