Материал по математике "Площади сечений многогранников"

В школы внедрена новая форма аттестации, и, следовательно, необходимо готовиться к ней. Если обратиться к кодификатору элементов содержания, проверяемых в задании С2 ЕГЭ , то в них представлены сечения куба, призмы, пирамиды и нахождение плоскости их сечения.

Эти задания почти отсутствуют в школьных учебниках и ученики могут испытывать затруднения при их решении. Поэтому в данной статье я хочу проанализировать решение задач на построение сечений несколькими методами, сделать подборку задач, предлагаемых различными центрами творческого образования в последние годы.

Несмотря на высокое дидактическое значение задач на построение сечений многогранников, их методические резервы практически не используются. Одна из основных причин сложившейся ситуации заключается в том, что эти задачи включаются в систематический курс стереометрии эпизодически. Поэтому данные задачи учителю следует самостоятельно включать на разных этапах изучения многогранников.

Система задач на построение сечений многогранников должна быть организована по принципам содержательно – методической линии и содержать задачи следующих типов:

- задачи непосредственно на построение сечений (при введении понятий многогранников);

- задачи на доказательство (при рассмотрении свойств многогранников);

- задачи на нахождение площади сечения (при разбиении его на простые многоугольники);

- задачи на нахождение площади сечения (при изучении теоремы о площади ортогональной проекции плоской фигуры).

1. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де ABCDA₁B₁C₁D₁ из­вест­ны рёбра AB=8, AD=7, AA₁=5. Точка W при­над­ле­жит ребру DD₁ и делит его в от­но­ше­нии 1:4 счи­тая от вер­ши­ны D. Най­ди­те пло­щадь се­че­ния этого па­рал­ле­ле­пи­пе­да плос­ко­стью, про­хо­дя­щей через точки C,W и A₁.

2. Пло­щадь бо­ко­вой по­верх­но­сти пра­виль­ной четырёхуголь­ной пи­ра­ми­ды SABCD равна 108, а пло­щадь пол­ной по­верх­но­сти этой пи­ра­ми­ды равна 144. Най­ди­те пло­щадь се­че­ния, про­хо­дя­ще­го через вер­ши­ну S этой пи­ра­ми­ды и через диа­го­наль её ос­но­ва­ния.

Весь материал - в документе.

Площади се­че­ний многогранников

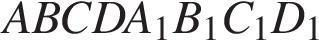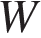1. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­ны рёбра Точка при­над­ле­жит ребру 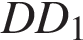и делит его в от­но­ше­нии 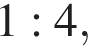счи­тая от вер­ши­ны 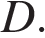Най­ди­те пло­щадь се­че­ния этого па­рал­ле­ле­пи­пе­да плос­ко­стью, про­хо­дя­щей через точк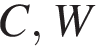и и

2. Пло­щадь бо­ко­вой по­верх­но­сти пра­виль­ной четырёхуголь­ной пи­ра­ми­ды SABCD равна 108, а пло­щадь пол­ной по­верх­но­сти этой пи­ра­ми­ды равна 144. Най­ди­те пло­щадь се­че­ния, про­хо­дя­ще­го через вер­ши­ну S этой пи­ра­ми­ды и через диа­го­наль её ос­но­ва­ния.

3. В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC с ос­но­ва­ни­ем ABC угол ASB равен 36°. На ребре SC взята точка M так, что AM — бис­сек­три­са угла SAC. Пло­щадь се­че­ния пи­ра­ми­ды, про­хо­дя­ще­го через точки A, M и B, равна Най­ди­те сто­ро­ну ос­но­ва­ния.

4. В пра­виль­ной четырёхуголь­ной пи­ра­ми­де SABCD с ос­но­ва­ни­ем ABCD про­ве­де­но се­че­ние через се­ре­ди­ны рёбер AB и BC и вер­ши­ну S. Най­ди­те пло­щадь этого се­че­ния, если бо­ко­вое ребро пи­ра­ми­ды равно 5, а сто­ро­на ос­но­ва­ния равна 4.

5. В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де PABCD, все ребра ко­то­рой равны 4, точка K ― се­ре­ди­на бо­ко­во­го ребра AP.

а) По­строй­те се­че­ние пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точку K и па­рал­лель­ной пря­мым PB и BC.

б) Най­ди­те пло­щадь се­че­ния.

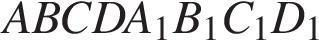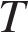6. На ребре пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да взята точка так, что Точка — се­ре­ди­на ребра 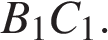Из­вест­но, что

а) До­ка­жи­те, что плос­кость 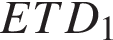делит ребро 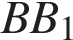в от­но­ше­нии

б) Най­ди­те пло­щадь се­че­ния па­рал­ле­ле­пи­пе­да плос­ко­стью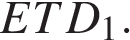

7. В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де PABCD, все ребра ко­то­рой равны 4, точка K ― се­ре­ди­на бо­ко­во­го ребра AP.

а) По­строй­те се­че­ние пи­ра­ми­ды плос­ко­стью, про­хо­дя­щей через точку K и па­рал­лель­ной пря­мым PB и BC.

б) Най­ди­те пло­щадь се­че­ния.

8. Ос­но­ва­ни­ем пря­мой че­ты­рех­уголь­ной приз­мы ABCDA₁B₁C₁D₁ яв­ля­ет­ся квад­рат ABCD со сто­ро­ной , вы­со­та приз­мы равна . Точка K — се­ре­ди­на ребра BB₁. Через точки K и С₁ про­ве­де­на плос­кость α, па­рал­лель­ная пря­мой BD₁.

а) До­ка­жи­те, что се­че­ние приз­мы плос­ко­стью α яв­ля­ет­ся рав­но­бед­рен­ным тре­уголь­ни­ком.

б) Най­ди­те пе­ри­метр тре­уголь­ни­ка, яв­ля­ю­ще­го­ся се­че­ни­ем приз­мы плос­ко­стью α.

9. В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC сто­ро­на ос­но­ва­ния AB равна 12, а бо­ко­вое ребро SA равно 13. Точки M и N — се­ре­ди­ны рёбер SA и SB со­от­вет­ствен­но. Плос­кость α со­дер­жит пря­мую MN и пер­пен­ди­ку­ляр­на плос­ко­сти ос­но­ва­ния пи­ра­ми­ды.

а) До­ка­жи­те, что плос­кость α делит ме­ди­а­ну CE ос­но­ва­ния в от­но­ше­нии 5 : 1, счи­тая от точки C.

б) Най­ди­те пло­щадь мно­го­уголь­ни­ка, яв­ля­ю­ще­го­ся се­че­ни­ем пи­ра­ми­ды SABC плос­ко­стью α.

10. В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC сто­ро­на ос­но­ва­ния AB равна 24, а бо­ко­вое ребро SA равно 19. Точки M и N — се­ре­ди­ны рёбер SA и SB со­от­вет­ствен­но. Плос­кость α со­дер­жит пря­мую MN и пер­пен­ди­ку­ляр­на плос­ко­сти ос­но­ва­ния пи­ра­ми­ды.

а) До­ка­жи­те, что плос­кость α делит ме­ди­а­ну CE ос­но­ва­ния в от­но­ше­нии 5 : 1, счи­тая от точки C.

б) Най­ди­те пло­щадь мно­го­уголь­ни­ка, яв­ля­ю­ще­го­ся се­че­ни­ем пи­ра­ми­ды SABC плос­ко­стью α.

11. В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC сто­ро­на ос­но­ва­ния AB равна 12, а бо­ко­вое ребро SA равно 13. Точки M и N — се­ре­ди­ны рёбер SA и SB со­от­вет­ствен­но. Плос­кость α со­дер­жит пря­мую MN и пер­пен­ди­ку­ляр­на плос­ко­сти ос­но­ва­ния пи­ра­ми­ды.

а) До­ка­жи­те, что плос­кость α делит ме­ди­а­ну CE ос­но­ва­ния в от­но­ше­нии 5 : 1, счи­тая от точки C.

б) Най­ди­те пло­щадь мно­го­уголь­ни­ка, яв­ля­ю­ще­го­ся се­че­ни­ем пи­ра­ми­ды SABC плос­ко­стью α.

12. В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC сто­ро­на ос­но­ва­ния AB равна 24, а бо­ко­вое ребро SA равно 19. Точки M и N — се­ре­ди­ны рёбер SA и SB со­от­вет­ствен­но. Плос­кость α со­дер­жит пря­мую MN и пер­пен­ди­ку­ляр­на плос­ко­сти ос­но­ва­ния пи­ра­ми­ды.

а) До­ка­жи­те, что плос­кость α делит ме­ди­а­ну CE ос­но­ва­ния в от­но­ше­нии 5 : 1, счи­тая от точки C.

б) Най­ди­те пло­щадь мно­го­уголь­ни­ка, яв­ля­ю­ще­го­ся се­че­ни­ем пи­ра­ми­ды SABC плос­ко­стью α.

13. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де 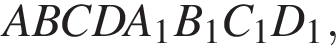из­вест­ны рёбра: Точка при­над­ле­жит ребру 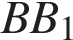и делит его в от­но­ше­нии счи­тая от вер­ши­ны Най­ди­те пло­щадь се­че­ния этого па­рал­ле­ле­пи­пе­да плос­ко­стью, про­хо­дя­щей через точки и

14. Точка — се­ре­ди­на ребра куба Най­ди­те пло­щадь се­че­ния куба плос­ко­стью если ребра куба равны

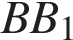15. Точка  — се­ре­ди­на ребра куба Най­ди­те пло­щадь се­че­ния куба плос­ко­стью если ребра куба равны